고뇌의 고통이 없는 켤레 경사도 기법 개론(1과 1/4판)

VisCom TR Series - Copyright c Jonathan Richard Shewchuk and VisCom Commune.
LLLsss¦¦¦LLL {{{™™™ŠŠŠªªªEEEPPPêêêŸŸŸªªªÁÁÁ(11
4XXX)
–––{{{†
, ‡‡‡ôôô‘‘‘‡
, îîî–––|||††
, êêêõõõ‡‡
bbb
†
ôôôÂÂÂ¡¡¡ppp, ‡
ûûûÙÙÙÂÂÂ¡¡¡ppp, ††
ÙÙÙSSS½½½vvvqqqÂÂÂ¡¡¡ppp, ‡‡
ÙÙÙSSSÂÂÂ¡¡¡ppp
ÅÅÅccc
ŠªiPê(conjugate gradient) Ÿªù ™±µ¿vÇü™xÍèßð¦©õu ™Ú‚ 6lq
ŠÄª°. ” # Ý± Qê ¨ù þ sgõ ”¡# ”‘X z`ê { °Øv !°. ¢
þ¦ f%ù“šê6“ #™êt‘uu‚t¦y{™úžq4v!°. ¢î
¿Ÿª‚Â¢îê!™Ÿ X©™Ÿ(¡%¦Í“6¡úv ß¥Q©ë¢Ù`u¢…ý
3¦Yî“}°. “§ŠªiPê“ª†™Dù¢³ Vt€u#©£½!™ÍI¢Pv
¿Øqu!°. Š Û

¤[[¢ë%†V¾Iˆ¢v ê{•Ð½!™D°.
2òÍé¦]ú™¢, õÌ Š/Â (steepest descent), Šª“³(conjugate directions),
Šª iPê(conjugate gradient) Ÿªú îê£ D°. vî¯â™ b‘ü(Jacobi) Ÿª, /Â , Šª i
PêŸª#¦½¶úz` ™ÚPÌþD°. ”ývY

ý(preconditioning)‰üxÍŠªiPê“
ª#j¥üq!°. ›%™Š Û˜úÖQQ ²v¨ùd³ú •°. 66¦”¡úg‡
üT, ¢S‘Í×¦z`ù˜°°. ]ùa “t¿°ô“ª÷¿z`üv!÷TÂÙÛ¦“
eéù”‘Xz`‰¥Ùg‡ý°.1
1ÙW%- Jonathan Richard Shewchuk. Ù[g@- An Introduction to the Conjugate Gradient Method without the Agonizing Pain. Ùf
[¦u™j#°WuÊç(Natrual Science and Engineering Research Council of Canada)¦1967[W6¡PzYyY¡8
³(National Science Foundation)¦“Ù(Grant ASC-9318163)ú‹IØq€°. [t¦[bY@ÁùW%¦©6j#°W
uÊç(NSERC), yY¡8³(NSF), ÓùyveÙ¦©¿‹IŠut™Ký°.
1

VCTR-2006-F-002 vs¦v {™ŠªiPêŸªÁ(11
4
X)- –{†
, ‡ô‘‡
, î–|††
, êõ‡‡
b
‘‘‘ttt‚‚‚ÂÂÂ©©©
c 1994 by Jonathan Richard Shewchuk. W„™î%: ƒ5³ý

Ù
. ‘t™W„vè ”Â¿
Cs!v, ‘t¦Â ¿sˆ¢Ã’{™¢%îÄQÄ€üq•jþ½!°.
‘t™ Šª i€ê Ÿªú ¢ ÖQ ‡Ù v òù ¡f0ú òŸ æ Š §0q€°. 5‚Q
“X€¨, ½e©˜£ RÌ, ”ýv R §rÿ qi ‘ê¦ ”‘X z`†ê ”÷¦ x² sŸ †ˆ°
(jrs@cs.cmu.edu); 0 ÏÚÙ™£¥«X‚j¥þD°. 5™48‘tõ½zè¢‚ßÌ
¢€»‚‘î¨°.
ŠÄŸª‚Â©Ì¨ùDú‡Ù v% ™€Š0‚Q5™éýyõþß(William L. Briggs)¦“A
multigrid Tutorial” [2]ú8¢°. þù“š«“R ù½¡tX ÏÚ 60SŠ•þ°.
½X Ÿª‚ ‘© R xv !™ D¦ ’¾ÙÛú òsv ‘t¦ #v‚ ª !™ üeú g‡
© s}Ï ¡¥ò Íß(Omar Ghattas)‚Q 4»¢ §€õ ÿ°. üeú © s}Ï gß ‚xá(James
Epperson), Úü¡¬ ¢(David O’Hallaron), gßßGXdß(James Stichnoth), §3ª‡î(Nick Tre-
fethen), ”ýv°¦…ƒŽ(Daniel Tunkelang)‚Qê§€¢°.
›Å¢ÙÛ§úú½!êÀ¡`¦’Ò¦…”’’õÃ°:
copyright c Jonathan Richard Shewchuk and VisCom Commune
2

4
X)- –{†
, ‡ô‘‡
, î–|††
, êõ‡‡
b
1 qqq ŸŸŸ
›% Šªi€ê(conjugate gradient method)ú•Í²v°úX, 4–¦t¿°ô‘¶ú}™Ú, þ
0qiþ0“™š¦’8“wW°. ›%™þ0ú 5ê© “q°°. þ0ùÂÙÛ¢
³ QŠªi€êõŸÁ°÷T, qg¢”‘Xz`ê{}vqxQŠªi€êŸª

ü‚vuü}
™“‚Â¢@3(hint)ê{”Ÿª¦4úz` v!}°. ˜ù¢›%¦•`ÍÛ‚Ïf Q
ü}÷T, 6òŠªi€êŸªú•Í²™¡f0Ôˆß Ï“eé×qý s¦†„Ù vÍs¢
xvýú•ÍŸõ††VtSŠ€°.
Šªi€êŸªùxÍ“eé¦6Â¢èßðúŸæ© 6¨€Ìü™ŠÄª°. Šªi€
êŸªù°üÍ×¦èßð‚ssî‰X°.
Ax = b (1)
Xx™cò™¯âv, b™xv!™¯âTA™xv!™e“(square), Âa(symmetric), j¦e
ÙÒ(positive-define) ±µ°- Óùj¦ÙeÙÒ(positive-indefinite) ±µ½ê!°. “j¦eÙÒ” ˆ
|ú¦y ™“#q£¹°v£“†ê5|‚°è…•ÇD¦7e£›Å™{°. èßðù–yÛ
“eé, uƒÛu, ç¿Ûu, ½¡¾g5ú©d£X‘‘5Í5™î¢òÛª(finite difference)‰î¢Å
™ª(finite element method) 5‰ù|Å¢ª‚t%s5Í8°.
Šªi€êŸª‰ùŠÄ“ªù2™±µú€Ì£X‚X¦ °. A ƒ}¢iÍ‚ 6”ù“
ªùAõÛ© v‹XÞ(backsubstitution)‚¦©“eéú™D°. ƒ}¢AúÛ© ™Ú@ý™è
¢ù Â? èßðú ŠÄ©t ©d ™Ú @ý™ è¢‰ üæ °. ”ýv ¢¥ A Û©üV èßðù b¦
Š ©0úæ©t§òQÃô¿½!°. ƒ}¢±µúùEcý¾Ÿõ “™ÌÀ¾Ÿ¦2™
±µ‰ üp©Ã%. 2™±µ A¦ ˆ¡Å™(triangular factors)‚™ 0 s¨ Ù™ ŠX÷¿ Ù’¦ AÃ
°ýgÌ¨°. Û©% Ecý¦¢qX‘‚Ý £½ê!÷Tè¢¨@ ½ê!°. î“
q‹XÞú‰eŠÄŸªÃ°Ì— ½ê!°. ŠV‚ÂÙÛ¦ŠÄX“ªùEcýîñmv2
™±µ‚Â©§òQô¢°.
›%™Š ÛxÍÂ½¡ú½°°v e T, vî¯â¦vî©‰ùD‚Â©t™0cô°
v£“†ê±µ…‡‰xÍë¢5‚Â©t™0xv!°v e¢°. ¢ŸÆX eú†Ö÷¿
›%™Šªi€êŸª¦qõ ¢¢`Ÿ Qu9©5¤D°.
2 vvvŸŸŸªªª
a “e¦®vŸ‚Â©…•ÃVtè %.
3

4
X)- –{†
, ‡ô‘‡
, î–|††
, êõ‡‡
b
±µú vè Ÿ æ© Â‘%õ €Ì£ DT, ™‘%™ ¯âõ 5ÍR™Ú €Ìý°. ße†™ ”ýß
‘%¿vè¢°. A™n × n ±µvx®b™¯â, Œ, n × 1 ±µ°. ½é1ù°ü‰vÇ¢°.









A11 A12 · · · A1n
A21 A22 A2n
...
...
...
An1 An1 · · · Ann


















x1
x2
...
xn









=









b1
b2
...
bn









.
£ ¯â¦ 4X(inner product)ù xT
yv ße† ¦ n
i=1 xiyiú 5ÍT°. xT
y = yT
x°. x® y ”
p VxT
y = 0°. ŠX÷¿xT
y®yT
Ax®1 × 1 ±µü™vÇéùße†©÷¿D›ý°.
§™c(0s¨¯âx‚Â©°üÙ5éú§„£X, ±µA j¦eÙÒ(positive-deﬁnite)°.
xT
Ax 0 (2)
ŠŸtsˆ¢¦yõ—'“q¢°vì “†. “ù”°“”‘X“s¦qtj¦
eÙÒ±µ”©“wùD‰qxQ°òQÃ™“© ™DÑÏs¨°. õ© Ÿ
æ©t™j¦eÙÒ(positive-deﬁnite)†™D2òÍé‚qxQ–³úyX™“…•Ç›Å !°.
¥“¦÷¿(AB)T
= BT
AT
‰(AB)−1 = B−1
A−1
†™|Å¢ŸÆ¨5éú#“vŸr †.
3 2òòòÍÍÍééé
2òÍé(quadratic form)ù¢³8©°ü‰ùÍ×¦ße†©ú™2ò¥½°.
f(x) =
1
2
xT
Ax − bT
x + c (3)
A™±µvx®b™¯â°. ”ývc™ße†’½°. ›%™ŠŸtA ÂaXv(symmetric)
j¦eÙÒiÍ, Ax = b¦©õÌ Šf(x)õ/™Ü£½!üú¢³8Ã²¢°.
˜¦Y‚t›%™°ü‰¢³¢ìgšg‘gõ “v°j¢“úz`£D°.
A =


3 2
2 6

 , b =


3
−8

 , c = 0. (4)
4

4
X)- –{†
, ‡ô‘‡
, î–|††
, êõ‡‡
b
èßðAx = b ”¡1‚5Í5!°. ŠX÷¿©x™n ¦#eV(Ú¤)¦pòb°(X¡
¡¦ #eVù ¡¡ n − 1 òÙú •°). ‘g¦ ©™ x = [2, −2]T
°. Âÿü™ òé f(x)™ ”¡
2‚5Í8°. f(x)¦5vx¦cjù”¡3‰°. A j¦eÙÒŸX‘‚f(x)‚¦©e¦ü™v
Vùj“xÍ×¦€Œ‰ùcj°. (‚Â©2è‚Ì%ƒ8z` W°)
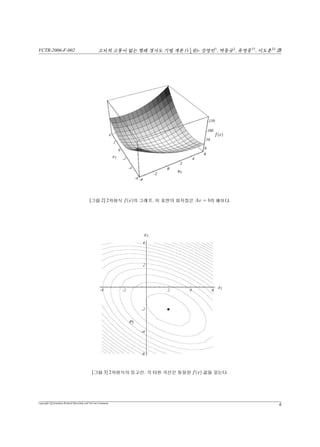
[”¡1] 2òÙxÍèßðš. ©™xÛ0¦pòb°
2òé¦ŸÐŸ(gradient)™°ü‰e¦ý°.
f (x) =









∂
∂x1
f(x)
∂
∂x2
f(x)
...
∂
∂xn
f(x)









. (5)
ŸÐŸ™sq•bx‚Â©, f(x)¦ 6À’ “³ú òÅ™¯â›°. ”¡4ù½é4 ‰
ù’½õ½é3‚Â Šuq•ŸÐŸ¯âõz` v!°. €Œcj¦j“V†±‚t™ŸÐŸ
0°. f (x)‚0üêÀ¥÷¿¦f(x)ù/™Ü£½!°.
°™“Ø¢zú ©½é5õ½é3‚Â Š°üúîê£½!°.
f (x) =
1
2
AT
x +
1
2
Ax − b. (6)
5

4
X)- –{†
, ‡ô‘‡
, î–|††
, êõ‡‡
b
[”¡2] 2òÍéf(x)¦”’’. vV¦/WbùAx = b¦©°.
[”¡3] 2òÍé¦5vx. ¡ÍÙwxùô¢f(x) ©ú™°.
6

4
X)- –{†
, ‡ô‘‡
, î–|††
, êõ‡‡
b
[”¡ 4] 2òÍé¦ ŸÐŸ f (x). c( x‚ Â Š, ŸÐŸ ¯â™ f(x) 6 ¾Q ’ç ™ “³ú ýÅT 5vx‚
”p¢°.
A ÂaV“eéù°ü‰¢œÜý°.
f (x) = Ax − b. (7)
ŸÐŸõ0÷¿ VÍý uv% ™xÍèßð½é1úu™°. ” t¿Ax = b¦©™f(x)¦
qb(critical point)°. A Âa`§s¦†j¦eÙÒ(positive-definite)†V©™f(x)¦/™©°.
H†tAx = b¦©™f(x)ú/™Ü ™xúüü÷¿¦u£½!°. (A ÂaX“w÷V½é6™Š
ªi€êŸªèßð 1
2 (AT
+ A)x = b¦©õüQý°™DúÃŠsv!°. X 1
2 (AT
+ A)™Âa
±µ°.)
Âaj¦eÙÒ±µù·©Q”ù—úv!ú«? qi¦¦bp‚t¦f®xÍèßð¦
©x = A−1
b €¦‘qõ…•Ã%. ½é3ú†Ö÷¿A ÂaiÍ(±µj¦eÙÒ(positivie-
definite)“‚‘q{) °ü¢¥úÃ½!°. (ÙÀC1).
f(p) = f(x) +
1
2
(p − x)T
A(p − x). (8)
A j¦eÙÒ(positive-definite)†v V, Ù5é2‚¦©ó%¦¨c(p = x‚Â©j½°.
™x f¦Y‹/™©úy¢°.
7

4
X)- –{†
, ‡ô‘‡
, î–|††
, êõ‡‡
b
j¦eÙÒ(positive-deﬁnite) ±µ‚‘¢ 6”‘X©™±µ¦2òÍéf(x) j“Vý°
™D°. A §™j¦eÙÒ s¦†V°ô  !°. A™ü¦eÙÒ þ½!™Ú™j¦
eÙÒ±µ‚Â©ÙÒõ†öd‰, Œ”¡2¦s’æõšqnùcjý°. A 4±µiÍ
‚™î¢© {™iÍ°; ©¦š¦ù 5¦”x, Óùe¢f ©ú “™#eV(hyperplane)
ý°. A æ‚t z`¢ qi iÍê s¦†V, x™ u6b(saddle point) üT /Â 5 Šª i€ê
Ÿª5ìg£D°. ”¡5™ ¢  0úÃŠsv!°. b®c¦©ùj“Í¦/™bq7
“õde¢°. ” 5j“Ícj‚™–³úyX“w™°.
xÍèßðú · Ì q²× Ã™ ‘g¿ ºÍ£«? /Â ‰ Šª i€ê Ÿª 5¦ “ª0ù ”¡
1® #eV¦ pòõ ©t s¦† ”¡ 2® ¥½¦ /™Üõ © ”‘X ©    Ÿ
X‘°.
4 ///ÂÂÂ   “““ªªª
/Â “ª‚t™, qi¦bx(0)‚tè Šj“x¦…†±÷¿y uR²¢°. ©x‚?Û
8 «Qü™ƒ8ú§„£X«“¡³qx(0), x(1) · · · úD¢°.
5¦³q‚tf  6§òQ§™ ™“³úxØ¢°. “³ùf (x(i))¦ŠÂ“³°. ½é7‚
HòV, “³ù−f (x(i)) = b − Ax(i)°.
ŠŸtë%0Ÿr©˜£a “e¦õ™¢°. ¡ò(error) e(i) = x(i) − x™©¿Ùâv¥57
ýpqu!5õ5ÍR™¯â°. 54“(residual) r(i) = b−Ax(i)ùeÝ¢b ©÷¿Ùâv¥5ò
!5õ 5ÍT°. r(i) = −Ae(i)ù ÖQ x ½ !v, 54“™ dv ¡òõ ±µ Aõ Ì Š b® ù
‡¢÷¿ ºÞ¢ D÷¿ Ç ½ !°. Ì |Å¢ Dù r(i) = −f (x(i))†™ DT, 54“(residula)õ /Â
Ÿª¦•±“³‰ùD÷¿f¡ Š˜¢°. üxÍ‘g‚t™³“ó%¦e¦úXÌ Š14`
‚t f¦¢°. ” t¿ “54“(residual)”†™ Ìqõ Q üV “/Â “³”†™ ¦yõ g¤ý
êÀŸr©£†.
x(0) = [−2, −2]T
‚t ;Œ¢°v e %.

ü ½± ™ zù /Â (steepest descent) “³ú H
†t”¡6 (a)‚!™ìx’¦q7‚pq—D°. Œ, °ü‰”¿ÏqibúD£D°.
x(1) = x(0) + αr(0). (9)
‘g™ “³ú H† v¥5 •±¢ †ú xØ£ D °. (Œ, qi αõ xØ£ D õ de ™
D°.)
8

4
X)- –{†
, ‡ô‘‡
, î–|††
, êõ‡‡
b
[”¡ 5] (a) j¦ eÙÒ ±µú æ¢ 2òé. (b) ü¦ eÙÒ ±µú æ¢ 2òé. (c) ±µ(”ýv j¦ ÙeÙÒ).
qw¦ †±ú “#™ xÛ ©¦ š¦°. (d) ÙeÙÒ ±µ X. © K6 bŸ X‘‚ /Â ‰ Šª i€ê
ŸªXÌü“M™°. 3òÙ#”’‚t™±µ‹èK6cjú —½!°.
9

4
X)- –{†
, ‡ô‘‡
, î–|††
, êõ‡‡
b
[”¡6] /Â “ª. (a)x(0) = [−2, −2]T
‚t;Œ©tf¦/Â ¦“³÷¿¢³qõD¢°. (b) £V¦pòx
’‚ !™ b0 |‚t fõ /™Ü ™ bú ü™°. (c) j“xù £ V(2òÍé j“V‰ Ò•x “³¦ ½” eV)
pò ™x°. (d) /Wb‚t¦ŸÐŸ™Y³q¦ŸÐŸ®”p¢°.
10

4
X)- –{†
, ‡ô‘‡
, î–|††
, êõ‡‡
b
[”¡ 7] Ò• ”x(ìx Ü…v)ú H† Š †‚t ŸÐŸ f õ ÃŠsv !°. xÛæ¿ ¡ ŸÐŸ¦
– ‹è Ãv
!°(bx Ü…v). ŸÐŸ ¯â™ f¦ ŸÐŸ¦ ’ “³ú #Í4v
–ù Ò•xú H† ¤ X¦ ’ ñú #Í6°.
Ò•x’‚tŸÐŸ Ò•x‰”p ™†‚tf /™©ú™°.
[”¡8] ŠŸ, /Â ¦“ªù[−2, −2]T
‚t;Œ v[2, −2]T
‚t½¶¢°.
11

4
X)- –{†
, ‡ô‘‡
, î–|††
, êõ‡‡
b
”xÒ_(line search)ù”xúH†fú/™Ü ™αõxØ ™‰e°. ”¡6 (b)™‰eúz`
¢°. ½”eV‰j“V§5™pòxæ¦¢búxØ êÀg™¢°. ”¡6 (c)™£eV¦pò
‚¦©e¦ýj“x°. j“x¦/Wb‚tα©ùv¥ ?
ŸÆX yXÛú ©, α™ “³ ê¥½(directional derivative) d
dα f(x(1)) 0X fõ /™Ü¢°.
©ñ(chain rule)‚ ¦©, d
dα f(x(1)) = f (x(1))T d
dα x(1) = f (x(1))T
r(0) °. ½éú 0÷¿ v, r(0)®
f (x(1))0”püQ ™α xØüq˜¢°(”¡6 (d)õÃ†).
£ ¯â /™b‚t t¿ ”p üq˜ ™ ”‘X î !°. ”¡ 7 ™ Ò•xú H†t °
j¢ b0‚t ŸÐŸ ¯âõ ÃŠsv !°. j“x(”¡ 6 (c)) æ¦ ¦¦ b‚t “™ j“x ŸÐŸ
©(slope)™”b‚t¦2òÍé “™ŸÐŸ(gradient)õÒ•”xæ‚–°úX(”¡7, bxÜ…
v) fŸ™¯â¦£®°. –ý¯â0ùÒ•xúH†¤Xf¦’ íúvÇ¢°. f™–ý
ŸÐŸ¯â¦£ 0†-ŸÐŸ Ò•x‚”p ™†-‚t/™©ú™°.
αúde Ÿæ©, f (x(1)) = −r(1)‚î¦ V°üúuú½!°.
rT
(1)r(0) = 0
(b − Ax(1))T
r(0) = 0
(b − A(x(0) + αr(0)))T
r(0) = 0
(b − A(x(0))T
r(0) − α(Ar(0))T
r(0) = 0
(b − Ax(0))T
r(0) = α(Ar(0))T
r(0)
rT
(0)r(0) = αrT
(0)(Ar(0))
α =
rT
(0)r(0)
rT
(0)Ar(0)
õc£Â©ÃV, /Â (Steepest Descent) Ÿªù°ü‰°.
r(i) = b − Ax(i), (10)
α(i) =
rT
(i)r(i)
rT
(i)Ar(i)
, (11)
x(i+1) = x(i) + α(i)r(i). (12)
12

4
X)- –{†
, ‡ô‘‡
, î–|††
, êõ‡‡
b
šg™”¡8‚t®½¶£X«“½±ý°. “”8”i¿‚î¦ %. ™¡¡¦ŸÐŸ
Y¦ŸÐŸ‚Â©”p ŸX‘‚5Í5™Ç’°.
æ‚s›¢xvýù¢¥¦ŠÄX¥°£¦±µ-¯â…‡úÅu¢°. /Â (Steepest De-
scent) Ÿª¦qƒüÌù±µ-¯â…‚¦©•Íü™Ú, °±8ê ÏÚ 5™{’½ !°.
½é12¦jº¦ˆ‚−Aú… vbúÌ V°üúu™°.
r(i+1) = r(i) − αAr(i). (13)
r(0)úqƒ Ÿæ©½é10ú¢¥qƒ ™DùŠè›Å “§, ”ó¦ŠÄ‚t™½é13õ
qš©t €Ì£ ½ !°. ½é 11‰ ½é 13 c£‚t 5Í5™ ±µ-¯â … Arù ¢ ¥§ qƒ V ý°.
é§úÌ ŠŠÄú£XfŸ™‘gbù½é13ú ©e¦ü™½Žx(i) ©÷¿Ùâqiü
5(feedback)ê{fý°™b°. H†tÙô™½bŠ¤¡¡ê¦€X÷¿¢eÝ¢x s¦
†”–

¦qib‚½¶£½!°™D°. ¢³bù½é10úÌ ŠsŸX÷¿eÝ¢54
“(residual)õ°èqƒ¥÷¿¦©d£½!°.
/Â (Steepest Descent) Ÿª¦½¶‚Â¢ÛuY‚, Š Û0vî¯â‚Â¢Ýì¢©õ
£½!êÀ2®˜£¿§“²v¢°.
5 vvvîîî¯¯¯âââ(eigenvector)®®®vvvîîî©©©(eigenvalue)‚‚‚ÂÂÂ¢¢¢vvvööö
›% xÍÂ½¡¢‰dú½¢ó‚, vî¯â(eigenvector)®vî©(eigenvalue)ˆ|“êˆ“x
½ {}°. Š Û0ú òZ€ ›%õ òZ€®üæ °V, vî©“g“ ™Dú “v
‘gõ{™“ªùg¡òW“§d‘”D0êÂˆ|““•e÷¿” © v!•wúD°. Ý
± Qêvî¯â®vî©‚Â¢”‘X© {°V, Šªi€êŸª‹è© “q£D
°. Š Û§™vî¯â¦vî©¦ ™D0‚Â©Ív88 ú “v!°V`ú8glq
êý°.
vî¯â0ùŸÆX÷¿Ûuêu¿t€Ìý°; /Â (Steepest Descent) Ÿª5Šªi€êŸ
ªùxvýú½± Ÿæ©vî¯âõqƒ£›Å™{°.
5.1 vvvîîî©©©gggvvvîîî?
±µ B¦ vî¯â v™ Bõ XÌ Š ºÞú Šê “Í¦ ºÜ q5“ w™ 0 s¨ ¯â°(eÝ
QŠÂ“³÷¿ºÞü™Dùg½). v™£ º 65”“³ŠÂ þ½™!“§, ˜÷¿î“
13

4
X)- –{†
, ‡ô‘‡
, î–|††
, êõ‡‡
b
™wúD°. °è©, Bv = λvqiße†’½λ …8¢°. Xλ ©B¦vî©°. ¦¦
’½α‚Â©, ¯âαvê‹èô¢vî©λõ™vî¯â°. ™B(αv) = αBv = λαvŸX‘
°. °è©, vî¯âõ¾Ÿõš65vŠêŠY8vî¯â°.
@·êi¦˜£«? ŠÄªù‘‘Bõqi¯â‚qš©tŠÄXÌ Š©õu¢°. B  5
¦ vî¯â‚ ŠÄX÷¿ XÌþ X, °ü £ “ ÏÚ 5¦ ’á Œf£ ½ !°. |λ| 1 iÍ†
V, i ˆ¢Â¿¤XBi
v = λi
v™0 ¯â¿½¶£D°(”¡9). |λ| 1 V, Bi
v™ˆ¢Â¿v—D
°(10). ¥B XÌþX¥°, ¯â™|λ|¦©‚H†v“65s“Qý°.
[”¡9] v™−0.5¦vî©‚Âÿü™B¦vî¯â. i ’  V, Bi
v™0‚½¶¢°.
[”¡10] š‚tv™vî©2õ “™vî¯â°. i ’  V, Bi
v™ˆ¢Â¿Œƒ¢°.
B Âa±µ iÍ(‘‘ ”©“ wù iÍ‚ê    °), B™ xÍX ë¢ n ¦ vî¯âõ
•°. õ v1, v2, · · · , vn† vŸ %. š¦ù î “ w°. ™ ¡ vî¯â 0 s¨ X¾¢ ’
½§Â ¾Ÿ ºiþ ½ !Ÿ X‘°. ¡¡¦ vî¯â™ %ê‚Q Âÿü™ vî©ú “™Ú, õ
λ1, λ2, · · · , λn¿ vè %. vî©0ù sq• ±µ‚ Â© î Q e¦ý°. vî©ù t¿ ù ©ú
—½ê!vt¿°õ½ê!°. šõ0q, ¨5±µI¦vî©ùc£1v, 0 ¯â s¨¦¦¯
â I¦vî¯â°.
B vî¯â s¨ ¯â‚ XÌüV qi q@«? xÍÂ½ú ©¥‚ !q Í |Å¢ Ÿ
Á-`‚t òXv% ™”ŸÁ-ù 5¦¯âõ±ôx²•°ô¯â¦¦÷¿¢s ™D°.
vî¯â0¦š¦{vi} Rn
¦ŸWõØ™’áúv²©Ã%(Âa±µB™xÍë¢n¦vî¯
14

4
X)- –{†
, ‡ô‘‡
, î–|††
, êõ‡‡
b
â0ú •°). ¦¦n-òÙ¯â™0vî¯â0¦xÍƒ¦÷¿vÇþ½!°. ¢±µ‰¯â¦
…ùÛ•ªYXÌüt¿¡¡¦vî¯â‚…©“™B¦î‰™ë¢X÷¿ƒ€£½!°.
”¡11‚t¯âx™£vî¯âv1‰v2¦¦÷¿5Í5!°. Bõx‚… ™DùBõvî¯â0
‚ ¡¡ … Š ¦ú u ™ D‰ °. Bõ ŠÄ©t …© 5 V, Bi
x = Bi
v1 + Bi
v2 = λi
2v2 ý°. c
(vî©¦¾Ÿ 1Ã°÷V, Bi
x™0‚½¶ú£D°. (™xúu v!™vî¯â0c£
BõŠÄX÷¿…£iÍ0‚½¶ ŸX‘°). vî©0| 5†ê1Ã°À©ú™°V, x™ˆ¢
Â‚ Œƒ£ D°. D †¿ ½X©u ¡%0 ±µ¦ ßˆ3¤ Ši(spectral radius)‚ |Åú ÙŠ
™î°. ±µ¦ßˆ3¤Šiù°ü‰°.
ρ(B) = max |λi|, λi ùB¦vî¯â
x 0‚§òQ½¶ ŸõÙ Vρ(B)ù1Ã°s˜ v, VùD”°.
[”¡ 11] ¯â v(ìx Ü…v)™ vî¯â0(bx Ü…v)¦ xÍ ƒ¦÷¿ vÇþ ½ !°. ® ‘ý vî© λ1 =
0.7‰ λ2 = −2 °. B ŠÄX÷¿ XÌüV ¢ vî¯â™ 0‚ ½¶ v °ô #™ Œƒ¢°. H†t Bi
x ‹è
Œƒ¢°.
xÍ ë¢ n ¦ vî¯âõ ° ““ q ™ üÂa ±µw(
) …8¢°™ €ìú s›£ ›Å
!°. ù ±µ0ú Ù„ ±µ(defective matrix)†v ¢°. öù •`¢ xÍ Â½¡%0 ±
µ‚ Â© Ã™ ¾¢ Xîú 0 5ÍRv !°. ’ƒ¢ z`ù ‘t‚t °ØŸ‚ gˆ Ä3 “
§, Ù„ ±µ(defective matrix)¦ ±ô 4ù ŠÜý vî¯â(generalized eigenvectors)® ŠÜý vî
©(generalized eigenvalue)õÌ ŠÛu£½!°. Bi
x™0‚½¶ Ÿæ¢›Å?Ûƒ8÷¿c(Š
Üývî©(generalized eigenvalues)01Ã°ù©ú u˜¢°™ªYùŠY8îî “§, õ’
` ™DùÌÎq²×•°.
ŠŸt îÌ¢ €ìù °ü‰ °: j¦ eÙÒ ±µ¦ vî©ù c£ j°. €ìù vî©¦ e
¦õÌ Š°ü‰’`£½!°.
15

4
X)- –{†
, ‡ô‘‡
, î–|††
, êõ‡‡
b
Bv = λv
vT
Bv = λvT
v.
j¦eÙÒ(positive-deﬁnite) e¦‚¦ Š, vT
Bv™j°(–s¨v‚Â Š). H†tλ ‹èj
½ˆ‚{°.
5.2 bbb‘‘‘üüü(Jacobi) ŠŠŠÄÄÄªªª
0‚š’½¶ ™‰eús™DZu0€‚tŸõ™Ú‚êÓü™Dù“Ás¨°. ˆÌ
îÌ¢ ‰eú …•Ã%: Ax = bú Ÿ æ¢ ˜‘ü(Jacobi) “ª°. ±µ A™ £ ÙÛ÷¿ Ûý(split)ý
°: A¦Â¡Ûú”Â¿v°ôÛ0ùc£0D®Â¡xÛùc£0v°ôÛ0ùA®
ùE. H†tA = D + E°. %‘ü“ªù°ü‰°:
Ax = b
Dx = −Ex + b
x = −D−1
Ex + D−1
b
x = Bx + x, where B = −D−1
E, z = D−1
b. (14)
D Â¡±µt¿ÖQ‹±µúu£½!°. ¨5éù°ü‰ùbÜéú ©ÖQŠÄŸª
÷¿ºÞ£½!°.
x(i+1) = Bx(i) + z. (15)
sq• è ¯â x0‚ Â©, ½éù ´¦ ¯â0ú f¢°. Íý™ ŠÄŸªú © šX÷
¿5Í5™¯â0 5 5 ”Y¦©‰üp°úX©x‚Ì «×“Ÿõ†ˆ°. x™½é15¦v
eb†vÙò™Ú, ™x(i) = xXx(i+1)ê‹èx®ù©üŸX‘°.
ŠŸt¦½éîê‰e Í%¦X÷¿ÃD°. €ìîê™%¦XD°. ½é14 Âê
‚x‚Â¢¨5éúv¥(“§0qU½!°. €ìAõŠ “¿Ûý Ÿ§ V- Œ, æ¦š®°ô
D® Eú xØ Ÿ§ V - Íß-%Ý(Gauss-Seidel) “ª, 9ò š°Üª(Successive Over-Relaxation,
SOR) 5ú îê£ ½ !°. X ††™ †™ Íý xØ¢ Ûý “ª‚ ©¾ ™ B ù ©¦ ßˆ3¤
Ši(spectral radius)õ™D°. ŠŸt›%™–¦’˜‘˜Ûý“ªúxØ •°.
16

4
X)- –{†
, ‡ô‘‡
, î–|††
, êõ‡‡
b
¦¦qi¯âx(0)‚tè¢°v %. ¡ŠÄ‚Â©, Bú¯â‚XÌ¢‚zú”d‰‚Ì
¢°. ¡ŠÄ³q‚tqi§q“™ ?
5¦ ¯âõ Íý y 0 © v !™ °ô ¯â0¦ ¦÷¿ ŠŸ™ ÙYú °è ¢ ¥ XÌ© Ã
%. ŠÄú ©5Í5™x(i)úeÝ¢©x®¡òë(i)¦¦÷¿vÇ©Ã%. ” V½é15™°ü‰
ý°.
x(i+1) = Bx(i) + z
= B(x + e(i)) + z
= Bx + z + Be(i)
= x + Be(i) ½é14‚¦©,
∴ e(i+1) = Be(i). (16)
¡ŠÄùx(i)¦“eÝ¢ÙÛ”‚–³ús“w“§(x vebŸX‘°); ¥ŠÄX¥°¡ê
³ù–³ú‹™°. ½é16õ ©`–8x½!™bùρ(B) 1iÍ‚i ˆ¢Â¿c– V¡ò
ë(i) 0‚½¶¢°™D°. H†t#Ÿ¯âx(0)õqxQxØ —a /‘X©‚–³úyX“
q¢°.
“Áx(0)õqxQxØ —a‚H†sq•´Ì¡òR‚tx‚½¶ ™Ú‚›Å¢ŠÄì½‚™
–³úyXQý°. “§”–³ùßˆ3¤Šiρ(B)¦–³‚ü©ýgÑ|Å T, ßˆ3¤Šiù
½¶¦šêõde¢°. vj B¦vî¯â0 ÏÚ 6Àvî©ú “™(Œ, ρ(B) = λj ) vî¯â†
v %. vî¯â0¦xÍƒ¦÷¿vÇý#Ÿ¡òe(0) vj¦“³÷¿Ûú •°V, Û
6—ýQ½¶£D°.
B™ŠX÷¿Âaês¦v(üÀA Âa“†ê) Ý°Y£“êcô°. “§˜‘ü(Jacobi) “
ª¦ ½¶šê™ ρ(B)‚ ¾Q •ÍüT, ©ù ¢ ¢ A‚ µ²!°. Ý± Qê ˜‘ü Ÿªù c(
A‚Â©½¶ ™Dùs¦T, î“qj¦eÙÒ(positivie-definite)A‚Â©tê½¶ “wú½!
°.
5.3 uuuXXXššš
¢“0úuX÷¿ÃŸæ©, ›%™½é4‚5Í8šõqÃ²v¢°. 6W, vî©‰vî
¯âõü™“ª›Å °. e¦‚¦©vî©λõ “™¦¦vî¯âv‚Â©°ü¢¢°.
17

4
X)- –{†
, ‡ô‘‡
, î–|††
, êõ‡‡
b
[”¡12] A¦vî¯â™2òÍéf(x)‚¦©e¦ýj“V¦9“³‰X¢°. ¡¡¦vî¯â™‘ývî©
XÅ!°. ¡¡¦vî©ù©¾ü™i€¦ 7ôeê‚ü»¢°.
Av = λv = λIv
(λI − A)v = 0.
vî¯â™0 ¯â s¦°. H†tλI − A™4±µq˜¢°. H†t°ü¢¢°.
det(λI − A) = 0.
λI − A¦±µéú°¨é(characteristic polynomial)†Ùô°. Dùλ‚Â¢nò°¨é÷¿,
°¨é¦–(Y)±µA¦vî©ý°. ½é4‚!™A¦4°¨éù°ü‰°.
det


λ − 3 −2
−2 λ − 6

 = λ2
− 9λ + 14 = (λ − 7)(λ − 2),
°¨é¦–vî©t¿±µ¦vî©ù7‰2°. λ = 7Xvî¯â™°ü‰u£½!
°.
18

4
X)- –{†
, ‡ô‘‡
, î–|††
, êõ‡‡
b
(λI − A)v =


4 −2
−2 1




v1
v2

 = 0
∴ 4v1 − 2v2 = 0.
“eéú§„ ™¦¦© †¿vî¯â°. šõ0q, v = [1, 2]T
vî¯â°. ù“ª
÷¿vî©2‚©¾ ™vî¯â¿[−2, 1]T
õu£½!°. ”¡12‚tÇ½!™†®, vî¯
â0¾¢ÍÙ¦9‰X¢°™DúÇ½!°. ¢vî©¾VÌ›¢i€õ •°™DêÝ
£½!°. (ü½vî©ù”¡5(b)®5(d)‚Ã™D‰9úH†ô£Xf¦©§™¥ú¦
y¢°.)
g˜‘ü(Jacobi) “ªô ™cåúÃ%. ½é4‚!™’½0úÌ Š°ü‰ùŠÄé
úu™°.
x(i+1) = −


1
3 0
0 1
6




0 2
2 0

 x(i) +


1
3 0
0 1
6




2
−8


=


0 −2
3
−1
3 0

 x(i) +


2
3
−4
3


B¦vî¯âõu Vvî©−
√
2/3X[
√
2, 1]T
v, vî©√
2/3X[−
√
2, 1]T
°. 0ù
”¡ 13(a)‚t ”¡÷¿ 5Í5 !°. 0ù A¦ vî¯â® X “ w÷T, j“V¦ 9‰ê ’‘ {
°.
”¡13(b)™˜‘ü(Jacobi) “ª¦½¶úÃŠsv!°. xvý½±üVtH† ™êŸ¢
i¿™ŠÄŸªú ©šX÷¿5Í5™¡ò¨¡¡ “™vî¯âÛ0qxQºÜ ™“
…•È÷¿¦©£½!°.(”¡13(c), (d), (e)). ”¡13(f)™Ü…$vèõ ©vî¯âÛ0ú”ý
v!°. 0Ûù”¡11‚tÃ™†®¡¡¦vî©‚¦©deýšê¿½¶¢°.
›%™`ú ©Š Û0“vî¯â”†™D¾ê0¦v úÃTŽŸŸæ©p½0§0q
Th’¢v‘êu s¦†, ÍîÌ¢êu†™€ìúÝì8x…÷V”W°.
6 ///ÂÂÂ (Steepest Descent) ŸŸŸªªª¦¦¦½½½¶¶¶ÛÛÛuuu
6.1 ¢¢¢¥¥¥§§§‚‚‚©©©üüüŸŸŸ
/Â Ÿª¦ ½¶ú © Ÿ æ© Íx e(i) vî© λeõ “™ vî¯â†v %. ” V 54
19

4
X)- –{†
, ‡ô‘‡
, î–|††
, êõ‡‡
b
[”¡ 13] b‘ü “ª¦ ½¶. (a) B¦ vî¯â0 ¡¡¦ vî©‰ ¥Í #Í#!°. A¦ vî¯â® µý 0
vî¯â™ Ã“V¦ 9 I¦°. (b) b‘ü Ÿª [−2, −2]T
‚t è Š [2, −2]T
‚t ½¶¢°. (c,d,e) ¡ò ¯â
e(0), e(1), e(2)(ìx Ü…v)® 0¦ vî¯â Û(bx Ü…v). (f) Ü…$ù

ü 4 ¡ò ¯â¦ vî¯â Ûú
vÇ¢°. ¡òõvÇ ™¡¡¦vî¯âÛù0¦vî©‚H†š’£½!™šê¿0‚½¶¢°.
20

4
X)- –{†
, ‡ô‘‡
, î–|††
, êõ‡‡
b
“(residual) r(i) = −Ae(i) = −λee(i)ê‹èvî¯â°. é12õÌ Š°üúuú½!°.
e(i+1) = e(i) +
rT
(i)r(i)
rT
(i)Ar(i)
r(i)
= e(i) +
rT
(i)r(i)
λerT
(i)Ar(i)
(−λee(i))
= 0.
”¡ 14™ “ª · ¢ ¥§‚ ©‚ êµ ™“õ ÃŠu°. b x(i)™ ÍÙ¦ 9 ÏÚ 5‚ nŠ
!°. H†t54“™ÍÙ¦|îú†¿ ýÅQý°. α(i) = λ−1
e õxØ¥÷¿¦Œ¡X½¶úuú
½!°.
[”¡ 14] /Â (Steepest Descent) Ÿªù ¡ò¨ #¦ vî¯â¿ vÇþ iÍ ¢¥¦ ŠÄ§÷¿ eÝ¢ ©‚
½¶¢°.
ÌÎŠXÛuúæ©, e(i)õvî¯â¦xÍƒ¦÷¿vÇ©˜ T, ¢vî¯â0e‘
”p(orthonormal)q˜¢°. ÙÀC2‚t±µA ÂaiÍn ¦”pvî¯â …8¥ú’`¢
°. vî¯â™¦¦¾Ÿ¿ºi£½!ŸX‘‚¡¡¦vî¯âõe‘Ü£½!°. ©Qvî¯â
õxØ V°ü‰ùîÌ¢4ú™°.
21

4
X)- –{†
, ‡ô‘‡
, î–|††
, êõ‡‡
b
vT
j vk =



1, j = k,
0, j = k.
(17)
¡ò¨úvî¯â¦xÍƒ¦÷¿vÇ %.
e(i) =
n
j=1
ξjvj, (18)
Xξj™e(i)¦Û»£°. é17‰é18¿Ùâ°ü¦¨5éúu™°:
r(i) = −Ae(i) = −
j
ξjvj, (19)
||e(i)||2
= eT
(i)e(i) =
j
ξ2
j , (20)
eT
(i)Ae(i) = (
j
ξjvT
j )(
j
ξjλjvj)
=
j
ξ2
j λj, (21)
||r(i)||2
= rT
(i)r(i) =
j
ξ2
j λ2
j , (22)
rT
(i)Ar(i) =
j
ξ2
j λ3
j , (23)
é19™r(i) ‹èvî¯âÛ¦¦÷¿vÇþ½!üúÃŠsT, 0Û¦£™−ξjλj°. é
20‰22™†¿˜Ív†ß(Pythagoras)¦ªY°.
gÛuú©Ã%. é12‚t°üúuú½!°.
e(i+1) = e(i) +
rT
(i)r(i)
rT
(i)Ar(i)
r(i)
= e(i) +
j ξ2
j λ2
j
j ξ2
j λ3
j
r(i) (24)
¥“¦š‚tÍý™e(i) 5¦vî¯âÛ§ú —iÍα(i) = λ−1
e õxØ¥÷¿¦¢¥§‚
©‚½¶¥úÃ…°. ge(i) ¦¦©“§c(vî¯â ô¢vîXλõ “™iÍõ…•
Ã%. é24õÌ Š°üúu™°.
22

4
X)- –{†
, ‡ô‘‡
, î–|††
, êõ‡‡
b
[”¡15] /Â ùvî©c£°V¥«ŠÄ‚teÝ¢©‚½¶¢°.
e(i+1) = e(i) +
λ2
j ξ2
j
λ3
j ξ2
j
(−λe(i))
= 0
”¡15™“ª‹èŒ¡X÷¿©‚½¶¥úÃv!°. c(vî©0ô ŸX‘‚ÍÙù
uÍ(spherical)üqqiæX‚tè (‘q{54“(residual) u¦|îú ýÅQý°. αõ
xØ ™Dùˆ‚t®¥ô “¿α(i) = λ−1
¿xØ¢°.
” 5, a¦t¿°ôvî©…8£iÍqié÷¿α(i)õxØ Ì†êvî¯âÛ0úc
£g6£½™{°. H†tXxØ£½!™“ªù‘¦ÍÊý°. €ì, é24‚5Í5!™Û½
™λ−1
j ©‚Â© |Xe’÷¿Ç½!°. |Xξ2
j ™e(i)¦Û0 ÏÚÀÛ‚Íx¿æõ£Q
¢°. d‰X÷¿ ŠÄX¥°e(i)¦¥ùÛ0 ÏÚÙ™ìg¿£ šq5Ÿê¢°(üÀ–
Ù8™s¦“§). ¢î¿/Â Ÿª‰Šªi€êŸªù x(rougher)†vÙô°. ŠÂ¿%‘
üŸªùßˆÌ(smoother)Ú, ”î™c(vî¯âÛ0 ŠÄX¥°vq0ŸX‘°. /Â
‰Šªi€ê™½¡‘¶¦Ù‚t‘‘ßˆâ¿0qéüv!“§ìg¿™ßˆÌ s¦°.
23

4
X)- –{†
, ‡ô‘‡
, î–|††
, êõ‡‡
b
[”¡16] ”¡¦£¯â™ô¢‚C“i(norm)ú™°.
6.2 ŠŠŠ½½½¶¶¶
ŠXiÍ‚Â©/Â Ÿª¦½¶ú˜Ÿ ²V‚C“i(energy norm) ||e||A = (eT
Ae)1/2
ú
e¦©˜¢°(”¡16úÃ†). i(norm)ùîÁýi(Euclidean norm)Ã°°ØŸ ÑÍTqiV‚
t™ÌÎ%ß Ïi(norm)°; é8ú…•ÃV||e||Aõ/™Ü ™Ddvf(x(i))õ/™ ™D
úx½!°. i(norm)úÌ Š°üúuú½!°.
24

4
X)- –{†
, ‡ô‘‡
, î–|††
, êõ‡‡
b
||e(i+1)||2
A = eT
(i+1)Aei+1
= (eT
(i) + α(i)rT
(i))A(e(i) + α(i)r(i)) (½é12‚¦©)
= eT
(i)Ae(i) + 2α(i)rT
(i)Ae(i) + α2
(i)rT
(i)Ar(i) (½é14‚¦©)
= ||e(i)||2
A + 2
rT
(i)r(i)
rT
(i)Ar(i)
−rT
(i)r(i) +
rT
(i)r(i)
rT
(i)Ar(i)
2
rT
(i)Ar(i)
= ||e(i)||2
A −
(rT
(i)r(i))2
rT
(i)Ar(i)
= ||e(i)||2
A 1 −
(rT
(i)r(i))2
(rT
(i)Ar(i))(eT
(i)Ae(i))
= ||e(i)||2
A 1 −
( j ξ2
j λ2
j )2
( j ξ2
j λ3
j )( j ξ2
j λj)
(¨5é21, 22, 23‚¦©)
= ||e(i)||2
Aω2
, ω2
= 1 −
( j ξ2
j λ2
j )2
( j ξ2
j λ3
j )( j ξ2
j λj) (25)
Ûuùω¦’¢úü™D‚µ²!°. |X®vî©qxQ½¶‚–³úyX™“õÃŸæ©
n = 2iÍ‚Â©d‰õîê£D°. λ1 ≥ λ2†v %. ±µA¦ßˆ3¤ƒ8½(spectral condition
number)™κ = λ1/λ2 ≥ 1¿e¦ý°. e(i)¦ŸÐŸ(vî¯â‚¦©e¦ü™•vq‚Â©)™èb‚
¦…XTµ = ξ2/ξ1ý°. g°üéúu™°.
ω2
= 1 −
(ξ2
1λ2
1 + ξ2
2λ2
2)2
(ξ2
1λ1 + ξ2
2λ2)(ξ2
1λ3
1 + ξ2
2λ3
2)
= 1 −
(κ2
+ µ2
)2
(κ + µ2)(κ3 + µ2) (26)
ω¦©ù/Â Ÿª¦½¶šêõde Tµ®κ‚Â¢¥½¿”¡17‰”²•°. ”’
’¿ˆtÃ£ “šõÝ£½!°. §™e(0) vî¯â†VŸÐŸµ 0üT(Óùˆ¢), X
”’’‚tω 0ÿúÇ½!°. H†t½¶ùŒ¡X÷¿Øq•°. ¢vî©c£ô °V
ƒ8½κ 1üT, X‹èω 0ý°.
”¡ 18ù ”¡ 17¦ € Š ¡¡¦ –

‚ ©¾ ™ šõ Ãv !°. 0 ò Íé0ù vî¯â
‚¦©e¦ü™•vq‚t”²€°. ”¡18(a)®18(b)™Àƒ8½õ •š°. /Â ùèb
Ï ”Q xØü}°V §òQ ½¶¢° (”¡ 18(a)). ” 5 ŠX÷¿ κ À ©ú “V Í 5h
úÃ°(”¡18(b)). £¥«”¡ùÀƒ8½ ·5h“õ 6”‘X÷¿Ãv!°: f(x)™u
îÍ×õ§0T/Â Ÿªùuî¦jÅúµ°° T6¦•± “q ™’× ý°. ”¡
25

4
X)- –{†
, ‡ô‘‡
, î–|††
, êõ‡‡
b
18(c)® 18(d)‚t ƒ8 ½™ ù ©t¿ ò Íéù 6¦ uÍ ý°. X ½¶ù èb‚ ‘q {
§òQØq•°.
[”¡ 17] /Â (Steepest Descent) Ÿª¦ ½¶ê ω. ½¶ê ω™ µ (¡ò¨ e(i)¦ ŸÐŸ©)‰ κ (A¦ ƒ8 ½)¦
¥½°. ½¶ùµ®κ ù©X§ò°. veý±µ‚tµ = ±κX/J¦½¶úÃ°.
κõ’½¿£X(A veüq!÷t¿), ¢³¢yXÛú ©é26µ = ±κX/Â ÿúx½
!°. ”¡17‚tx‚¦©§0q“™2y¢õŸxúÇ½!°. ”¡19™Íý €Ì©µÏ±µ
A‚Â©/t¦èbú”ýv!°. èb0ùξ2/ξ1 = ±κ¿e¦ü™xæ‚n°. ω¦’¢(/
t¦èb‚©¾)ùµ2
= κ2
¿ze¥÷¿¦üú½!°.
ω2
≤ 1 −
4κ4
κ5 + 2κ4 + κ3
=
κ5
− 2κ4
+ κ3
κ5 + 2κ4 + κ3
=
(κ − 1)2
(κ + 1)2
ω ≤
κ − 1
κ + 1
.
(27)
é27¦Ù5é”¡20‚”²u!°. ±µ5h’×‚!ú½À(Œ, ƒ8½κ Á½À), /Â
¦½¶šê™ÌÎ—²•°. `9.2‚tÂaTj¦eÙÒ±µ°ü‰ùƒ8½õ •°V
é27n 2iÍ‚êŠY8¢¢°™Dú’`¢°.
26

4
X)- –{†
, ‡ô‘‡
, î–|††
, êõ‡‡
b
[”¡ 18] P šg™ ”¡ 17¦ P Š‚ ©¾ ™ “b –

õ vÇ¢°. (a)™ À κ, ù µ. (b) #h ½¶¦ š.
κ®µ c£¾°. (c) ùκ®µ. (d) ùκ®Àµ.
27

4
X)- –{†
, ‡ô‘‡
, î–|††
, êõ‡‡
b
[”¡ 19] ìx0ù /Â Ÿª‚t /J¦ ½¶ú Ã™ èbú vÇ v !°. bxù ½¶ ‰e‚t 6X™
³q0úÃv!°. è/J¦“b‚tØq—iÍ, ”°ü³q‹è/J¦“y‚tØq•°. ¡¡¦
³q‚tj“V9(ç•Ü…v)õeÝ45ê¿pò Qý°. ŠŸtκ™3.5°.
κ = λmax/λmin,
™y/Âvî©‰/™vî©¦ü(ratio)°. /Â Ÿª¦½¶d‰™°ü‰°.
||e(i)||2 ≤
κ − 1
κ + 1
i
||e(0)||A, ”ýv (28)
f(x(i)) − f(x)
f(x(0)) − f(x)
=
1
2 eT
(i)Ae(i)
1
2 eT
(0)Ae(0)
(½é8‚¦©)
=
κ − 1
κ + 1
2i
.
7 ŠŠŠªªª“““³³³ŸŸŸªªª
7.1 ŠŠŠªªª
/Â (Steepest Descent) Ÿªù ‘‘ ”¡ 8‰ Y‚ y Ò•°Ï “³ú °è Ò•¢°. ”¢
28

4
X)- –{†
, ‡ô‘‡
, î–|††
, êõ‡‡
b
[”¡20] /Â ¦½¶ù±µ¦ƒ8½(condition number) ’ ¥‚H†JÜý°.
Ú ©Q ù “³¦ Ò•ú 5€qt Š ¥ ½±£ D s¦† 5¦ Ò• “³‚ Â© ˜£ 6
ýõ ¢ ¥‚ †¿ ¤ ½ !°V Ì E“ wú«? s7q™ °ü‰ °: Íx t¿ ”p ™ Ò_ “³
d(0), d(1), · · · , d(n−1)¦š¦ú€†Ã%. ¡Ò•“³‚Â©tÍý™¢¥¦³q¿y6x® 6 «Ï
³q«“ êÀ ™D°. X›Å¢•±6ýõx½!°V, c(Ò•“³‚Â©1 ¥¦Ò•§½
± Vüv, dvn ³qó‚©‚êµ£D°.
”¡21ù•v9úÒ•“³÷¿€Ì Šz` v!°. (½e) ³q‚t™eÝ¢x1-•v®X
£X«“Ò•ú•± T, £¥«(½”) ³q‚t™Ù ™©úuQý°. e(1)d(0)®½”úsd©
Ã†. õŠÜ V, ³q‚t°ü‰æXõxØ ™D°.
x(i+1) = x(i) + α(i)d(i) (29)
¢¥Ò•¢d(i) “³÷¿™ˆ÷¿Ì’Ò•›Å{êÀ Ÿæ©, e(e+1) d(i) t¿”p©˜
¢°™€ìúÌ Šα(i) ©úu¢°. ¢ƒ8úÌ Š°üéúuú½!°.
29

4
X)- –{†
, ‡ô‘‡
, î–|††
, êõ‡‡
b
[”¡21] ”p“³Ÿª. IÖQê“ªùÍý y»úNv!úiÍ‚§Ì£½!°
dT
(i)e(i+1) = 0
dT
(i)(e(i) + α(i)d(i)) = 0 (½é29‚¦ Š)
α(i) = −
dT
(i)e(i)
dT
(i)d(i)
(30)
Ý± Qê“ªù€ìVc{™“ª°. “ªú€Ì Šα(i)õqƒ ²Ve(i)õxs˜§
™Ú, e(i)õu°™Dùy©õxv!°™Dt¿‘g% y²!™’×D°.
¢‘gbú©d ²V, ”p ™Ò•“³s¦†A-”pÒ•“³ú€Ì Š˜¢°. £¯â
d(i) ®d(j) t¿A-”p™Šª(conjugate) ü²V°üƒ8ú§„©˜¢°.
dT
(i)Ad(i) = 0
”¡22 (a)™A-”p¯â qxQÃ™ õÃŠsv!°. ˜„xÈæ‚;³üq!°v’
’©Ã%. § Š Û ”¡ 22 (a)¦ jú ä3st ÍÙ Ù

¤ ÃX«“ 3s¾h°v f¡© Ã
%. ” V¯â0”¡22 (b)

¤ÃD°
”¿ÏÅu€¨ùe(i+1)®d(i) t¿A-”p(”¡23 (b))õØq˜¢°™D°. ”pƒ8ù/
30

4
X)- –{†
, ‡ô‘‡
, î–|††
, êõ‡‡
b
[”¡22] ”¡(b) ¯â¦û0”p t¿”¡(a) ¯â¦ûùA-”p°.
Â Ÿª‰¥ô “¿B•“³d(i)úH†t/™búü™D‰ô °. õÝ æ©, “³
ê¥½õ0÷¿£vs’®qÃ%.
d
dα
f(x(i+1)) = 0
f (x(i+1))T d
dα
x(i+1) = 0
−rT
(i+1)d(i) = 0
dT
(i)Ae(i) = 0
é30¦îê“ªúÌ Š, B•“³0t¿A-”p üêÀ ™α(i)™°ü‰vÇý°.
α(i) = −
dT
(i)Ae(i)
dT
(i)Ad(i)
(31)
=
dT
(i)r(i)
dT
(i)Ad(i)
(32)
½é30‰™µýéùqƒ °. é‚tB•¯â 54“(residual) ¯â®ô °V,
éùdv/Â Ÿª¦é‰ùDý°™b‚sd †(½é11ú÷v è¡).
“ªn ¦³qR‚xõqƒ£½!°™Dú’` Ÿæ©, ¡ò¨(error term)úB•“³0
¦xÍƒ¦÷¿°ü‰vÇ©Ã%.
31

4
X)- –{†
, ‡ô‘‡
, î–|††
, êõ‡‡
b
[”¡ 23] Šª “³ Ÿªù n ¦ ŠÄ 4‚ ½¶¢°. (a) ¥« ³q‚t™ qi “³ d(0)õ H† ½± ý°. e(1)
Šèd(0)‚A-”p©b¢°™g¢ƒ8úÌ Š/™bx(i)xØý°. (b) #Ÿ¡òe(0)™ç•Ü…v¿vèý
A-”p Û¦ ¦÷¿ vÇ£ ½ !°. Šª “³ Ÿª¦ ŠÄ ³q ¢ ¥ ½±þ X¥° 0 Û |‚t #¦
Ûò»¿g6ý°.
e(0) =
n−1
j=0
δjd(j) (33)
X δj ©ù ¢³¢ ½¡X Ÿpõ © uú ½ !°. B• “³0ù ’Ò A-”pt¿, dT
(k)Aõ ½é
33¦jº‚¡¡¦ˆ‚… V 5¦Ò•“³úg½¢°ôc(Ò•“³‚Âÿ ™δj ©0úg6
£½!°:
dT
(k)Ae(0) =
j
δjdT
(k)Ad(j)
dT
(k)Ae(0) = δ(k)dT
(k)Ad(k) (d ¯â¦A-”p‚¦ Šuq™)
δ(k) =
dT
(k)Ae(0)
dT
(k)Ad(k)
=
dT
(k)A(e(0) +
k−1
i=0 α(i)d(i))
dT
(k)Ad(k)
(d ¯â¦A ”p‚¦ Šuq™)
=
dT
(k)Ae(k)
dT
(k)Ad(k)
( ½é29‚¦ Šîê) (34)
32

4
X)- –{†
, ‡ô‘‡
, î–|††
, êõ‡‡
b
½é31‰34‚¦ Š, Íý™α(i) = −δ(i)úx½!°. €ìù¡ò¨‚Â¢”¿Ï‘búg‡
¢°. °ü½é‚tÃ™†®, xõu ™Û 5 5õüs5 ™‰eùdv¡ò¨úÛ
»¿ 5fg6©5 ™D÷¿Ç½!°.(”¡23(b)õÃ†)
e(i) = e(0) +
i−1
j=0
α(j)d(j)
=
n−1
j=0
δ(j)d(j) −
i−1
j=0
δ(j)d(j)
=
n−1
j=i
δ(j)d(j) (35)
n ¥¦ŠÄ5V, c(Ûg6üqe(n) = 0ý°; ’`.
7.2 ”””ŠŠŠ-ÙÙÙyyy!!!(Gram-Schmidt) ŠŠŠªªª
gA-”pB•“³÷¿Øq•š¦{d(j)}úu Ÿ§ Vý°. °±ß¥Qêõ¢³ Qf
™“ª!™Ú“ª†¿Šª”Š-Ùy!‰e(conjugate Gram-Schmidt process)°.
n¦xÍë¢¯âu0, u1, · · · , un−1õ “v!°v %. üÀÃ°“ XxØ Ÿ™
“§ •v 9ú n ¦ xÍ ë¢ ¯â¿ V ½ !ú D°. Ò• “³ d(i)õ §0q RŸ æ© Íx uiõ
“v£, ŠŸtY¦c(Ò•“³¯â(”¡24õÇD)®A-”p “w™c(Ûú °. °
v5tCs!™¯â †¿Y¦c(Ò•“³‰A-”pÒ•“³d(i) ý°. °ô¿ %V
d(0) = u0¿£v, i 0c(iÍ‚Â©°ü‰Ò•“³¯âõu£½!°.
d(i) = ui +
i−1
k=0
βikd(k) (36)
Xβik™i kiÍ‚Â Še¦ý°. ©0úu Ÿæ Š, δjõu£X€Ì¢D‰ô¢“ª
ú€Ì£½!°.
dT
(i)Ad(j) = uT
i Ad(j) +
i−1
k=0
βikdT
(k)Ad(j)
0 = uT
i Ad(j) + βijdT
(j)Ad(j), i j (d ¯â0€¦A-”p‚¦ Š)
βij = −
uT
i Ad(j)
dT
(j)Ad(j)
(37)
33

4
X)- –{†
, ‡ô‘‡
, î–|††
, êõ‡‡
b
Šª“³(conjugate direction) Ÿª‚”Š-Ùy3ŠªÜ(Gram-Schmidt conjugation)ú€Ì£X¦‘
gbù ”¿Ï Ò• “³ú de Ÿ æ© Y¦ c( Ò• “³ ¯â0ú Ecý‚ “v !q˜ ¢°™
DT, Ìu5YÒ•“³úde Ÿæ©t™c£O(n3
)¦ƒ›Å °™D°. €ì³æ£
¦9¯âõ†Ö÷¿ŠªÜ(conjugation)õ½± ŠÒ•“³0úde •°V, Šª“³Ÿªùd
v Íß™6ª(”¡25)‰ô¢Dý°. d‰X÷¿Šª“³ŸªùŠªi€êŸª-Šªi€
êŸª‹èŠª“³Ÿª¦¢‘ê°- 5Í5¢¢‘gõ©d£X«“6¦€Ìü“w…°.
Šª“³Ÿªú© ™Ú‚ªîXÅ™™(Šªi€êŸªê¥ô “°) ”¡25 ”¡21õ
š D‚ Ý‰ °™ Dú xsòý™ D°. Šª “³ Ÿªú ½±£ X(Šª i€ê Ÿªú j¥ Š),
”“ª€ìšq8(Óù¾Ÿ ºÍý) ‡¢‚tÇX”p“³(orthogonal direction) Ÿª÷¿‘gõ
v!™D‰°™DúŸr †.
[”¡ 24] £ ¯â¦ ”Š-Ùy! ŠªÜ(Gram-Schmidt conjugate). £ ¦ xÍ ë¢ ¯â u0® u1 ¯â‚t è¢°.
d(0) = u(0)¿ ze¢°. ¯â u1ù d0‚ A-”p(™ conjugate) u∗
® d0‚ e± u+
£ Û÷¿ Û©þ ½ !°.
ŠªÜóA-”pÙÛ§+Qüqd1 = u∗
ý°
7.3 ¡¡¡òòò¨¨¨¦¦¦///XXX
Šª“³Ÿªù°ü‰ù8y!™4œ!°: “ªù ¥¦³q‚tÒ• Ìý©æR‚t
/x¦©õu¢°. Ò•´Ìý–‹q7«? span{d(0), d(1), · · · , d(i−1)}™Ò•¯âd(0), d(1), · · · ,
d(i−1)‚¦©fü™i-òÙÙÛ‡¢TõDi†vvÇ %. e(i) ©ùe(0) + Di¿ÙâxØþ½!
°. ŠŸ‚t ™“/x¦©”†™Qˆáy«? Šª“³Ÿª/x¦©õü™°™DùŸª
e(0) + Di¦ÙÛ‡¢R‚t©úxØ£X||e(i)||A©/™ ü™©úxØ¢°™D°(”¡26ú
Ã†). €ì qi ¡%0ù ÙÛ ‡¢ e(0) + Di R‚t ||e(i)||A ©ú /™Ü¥÷¿¦ Šª i€ê (conjugate
gradient) îê Ÿê¢°.
ô¢ “ª÷¿ ¡ò¨ ‹è B• “³¦ xÍ ƒ¦÷¿ vÇþ ½ !÷T(½é 35), ¡ò¨¦ ‚g“
i(norm)ù°ü‰ù¦ƒvÇ÷¿5ÍU½!°.
34

4
X)- –{†
, ‡ô‘‡
, î–|††
, êõ‡‡
b
[”¡25] 9“³³æ¯âõ€Ì¢Šª“³Ÿªù Íß™6ª(Gauss Elimination)÷¿êN²u!°.
||e(i)||A =
n−1
j=i
n−1
k=i
δ(j)δ(k)dT
(j)Ad(k) (½é35‚¦©îê)
=
n−1
j=i
δ2
(j)dT
(j)Ad(j) (d ¯â¦A-”p‚¦ Šîê)
¦ƒ(summation) vÇé‚!™c(¨ùs”€Ìü“wùÒ•“³‚§‘üq!°. e(0) + Di
ÙÛ‡¢‚txØý¦¦°ô¯âe™¦ƒvÇéúÝ6°úX5Í5™D‰ô¢¨0ú u
˜ T, ™dve(i) Šè/™‚g“i(norm)ú •°™Dú’`¢°.
½éú © /Xú ’` •÷¦, i ”‘X÷¿ õ ©£ ½ !êÀ ©Ã%. Šª “³ Ÿª
¦ z ‰eú è¡X÷¿ vÇ£ ½ !™ /x¦ “ªù ”¡ 22® Íý z ™ ‡¢‰ “šq
8(stretched)” ‡¢út¿üp ™D°. ”¡27 (a)®27 (c)™Šª“³ŸªR2
‡¢‰R3
‡¢‚t
qxQ ô ™“õ ÃŠsv !°; ”¡‚t t¿ ½”÷¿ Ã™ x0ù t¿ ”p(orthogonal)¢°.
ŠV‚, ”¡27(b)®27(d)‚t™ô¢”¡úvî¯â9úH†š²ÍÙÍ5vxuÍ(spherical)
üêÀ¢D°. ”¡‚t½”÷¿Ã™x0ùt¿A-”p°.
”¡27(a)úÃVŠª“³Ÿª#Ÿ8eXx(0)‚tè T, Ò•“³d(0)õÌ Š¢³q
ô Š°ü8eXx(1) b‚t98v!°. X”¿Ï¡ò¯âe(1)™Ò•“³d(0)‰A-”p°.
35

4
X)- –{†
, ‡ô‘‡
, î–|††
, êõ‡‡
b
[”¡26] ”¡‚tq¨Q©•–‹e(0) + D2 = e(0) + span{d(0), d(1)}°. ÍÙù‚C“i(norm)e¢
©ú™5vx°. £³q ½±ý, Šª“³Ÿªùe(0) + D2 ’‚t||e(i)||A ©/™ ü™be(2)õüQ
ý°.
©Qüùx(1)qxQÙÛ‡¢x(0) + D1‚t/™b†™DúÃ6£½!ú«? »ù”¡27(b)‚5
Í5!°: e(1)®d(0) t¿A-”pŸX‘‚ŠŸÃ™šq8‡¢(stretched space)‚t£¯â ½
”úØv!°. ‚ ¯âe(1)ùô¢‚g“i(norm)¦¡òõ™(Œ, ô¢||e||Aõ “™) 5v
x0úvÇ ™ôîÙ0¦Š“ö°. H†tÙÛ‡¢x(0) +D1†¿x1nŠ!™ôîÙ-Œ, x(1)‰
ô¢ ‚g“ i(norm)¦ ¡òõ ™ 5vx-‚ c ™ ceV üT X ceV‰ 5vx c ™
“b†¿x(1)°.
Dù €ì ”ý g‰§¢ ù s¦°; y 7.1 `‚t …•Æ †® , Ò• “³‰ ¡ò¨ t¿
A-Šª†™€ìdvÒ•“³úH†fõ/™ÜèÅ™D(H†t||e||Aõ/™ÜèÅ™D)‰ô
°. ” 5Šª“³Ÿª£¥«³qõ½± Š£¥«Ò•“³d(1) “³÷¿||e||Aú½±¢‚
êŠY8||e||A Y‚€Ì°ÏÒ•“³d(0) “³‚t/™î“ý°™DúqxQÃ6£½!
ú«? i ¥¦ŠÄú½± v5V, qxQf(x(i)) ÙÛ‡¢x(0) + Di Y‚t/™Üþ½!™D«?
d(0)®d(1)™t¿A-”pŸX‘‚”¡27(b)‚t½”÷¿§8°. ŠŸtÒ•“³d(1)©xõ³
¢°Dù`–¢Ú, ”î™d(0) ¯â xõ|î÷¿ vx(1)õ“5™Ù‚Â©x(1)‚tc ŸX‘
°. ˆòÙšg™õÌÎ0ÃŠu°. ”¡27(c)®27(d) ¡¡‚™|îù£¦ÍÙý ”²
u !°. x(1)™ ½Ù ÍÙ æ‚ nŠ !v, x2)™ RÙ ÍÙ‚ nŠ !°. 0 ”¡ú ƒî8 …• Ã†:
eVx(0) + D2™ÀÍÙú ‰ T%òv!÷T, eVùRÙÍÙ‰x(2)‚tc ™eVý°. ©
x™eVs’¦ÍÙ¦|î‚!°.
”¡27(c)õÃVˆt¦—‘ú°èv½!°. §Š Û‰R x(1) æX‚t!™ÚÙÛ‡¢
36

4
X)- –{†
, ‡ô‘‡
, î–|††
, êõ‡‡
b
[”¡ 27] Šª “³ Ÿª¦ /X. (a) òÙ ‘g. ½”÷¿ §#™ x0ù t¿ ”p(orthogonal)¢°. (b)
“šq(stretched)” ‡¢‚t vÇý ô¢ ‘g. ŠŸt ½”÷¿ §#™ x0ù t¿ A-”p°. (c) ˆòÙ ‘g,
xõ |î÷¿ ™ £ ¦ ôî ÍÙ Ãv !°. ”x x(0) + D1ù ½Ù ÍÙ‚ Â© x(1)b‚t c¢°. eV
x(0) + D2™4ÙÍÙ‚Â©x(2)b‚tc¢°. (d) ˆòÙ‘gõšq‡¢(stretched space)÷¿¦húXcå.
37

4
X)- –{†
, ‡ô‘‡
, î–|††
, êõ‡‡
b
x(0) + D2 ’ú@q°¦Vt¡ò¦i(norm) ||e||õ/™¿£½!™†÷¿ô ²v¢°v e %;
”¢ÚÍý °©½!™†ùÒ•†³d(1)‚t«q@½ {°. §™Ò•“³d(1)/™bú†
¿ ýÅv!°VÍý¦dvõµ£½!°. Ò•¯âd(1)/™búy6 ýÅv!°vÃ6
£½!™î !™ ?
”¡27(d) ”»úÃŠu°. d(1)d(0)‚Â ŠA-”pt¿, ”¡‚tt¿½”÷¿§5v!
°. gŠ ÛeVx(0) + D2‚eV¢6¦‘D

¤f¡ vs’õ°Ã%; XÃQ
ü™6Vù”¡27(b)®ô£D°. bx(2)ù‘¦|îþDv, bx™‘¦s’Å‚!Qü
™Ú, ”æX™x(2)‚t½”÷¿y6s’¿R²¢æX þD°. d(1)‰d(0)½”÷¿§5v!÷
t¿, Ò•“³d(1)™eÝ8x(2)õ³ QüT, x(2)™eVx(0) + D2 ’‚!™b0 ÏÚ©x‚
6 «ÏbþD°. eVx(0) + D2™x(2) nŠ!™u‚c ™eV°. ŠŸtƒ¥«³qõ½
± QüV, D2®A-”p ™“³÷¿Ó”Šx(2)‚t©x¿y6R² QþD°.
”¡ 27(d)‚t ˆá §q“™“õ © ™ °ô “ªù Š Û %ê © x‚ tt ÙÛ ‡¢
x(0) + Di‚t§Ó”êÀg¢üq!™uâú÷¿3s¾Ÿv!°v’’ ™D°. ³q¥°
Ý6 ™ÙÛ‡¢(expanding subspace) D¦òÙ 5fšq5v, X¥°uâùƒšfÌŠ Û
«° ¤½!êÀ%î¿×—D°. g‡¢úé” r²”¡27(b)

¤ÃQ§0V”D†
¿Šª“³Ÿªý°.
Šª “³ Ÿª¦ °ô |Å¢ 4 0 ”¡‚ 5Í5 !°. Íý™ ¥¦ ½± ³q‚t #e
V(hyperplane) x(0) + Di x(i) nŠ!™ÍÙ‚c Qý°™Dú…•Ã…°. 4 `‚z`¢†®
¦¦b‚t “™54“(residual)™“bú“5™ÍÙvV‰”p¢°™€ìúŸr †. D
ùdvr(i) Di®”p¢°™Dú¦y¢°. õ½¡X÷¿ÃŸæ©é35‚−dT
(i)Aõ¡¡¦jº
ˆ‚…©Ã%.
−dT
(i)Ae(i) = −
n−1
j=i
δ(j)dT
(i)Ad(j) (38)
dT
(i)r(j) = 0, i j (d-¯â¦A-”p‚¦ Š.) (39)
¨5éù°ô“ª÷¿îê£½ê!°. Ò•“³‚Â©¢¥¦³qõ½± v5Vˆ÷¿Ì
’ù”“³÷¿Ò•£›Å {°™€ìú’Ÿ %; ¡ò¨ùY¦c(Ò•“³‚Â©¨’A-”
pT, r(i) = −Ae(i)t¿54“(residual)™Y¦Ò•“³‰sg5”p ý°.
Ò•“³u ¯â0úÌ Š§0q€÷t¿, u0, · · · , ui−1 f ™ÙÛ‡¢†¿DiT, 5
4“(residual) r(i)™ ¢Yu¯â®”p¢°(”¡28úÃ†). Dù½é36‰r(j)¦RXúD Š
’`£½!°.
38

4
X)- –{†
, ‡ô‘‡
, î–|††
, êõ‡‡
b
dT
(i)r(j) = uT
i r(j) +
i−1
k=0
βijdT
(k)r(j) (40)
0 = uT
i r(j), i j (½é39‚¦ Š) (41)
ˆ÷¿ €Ìþ ¨5é 5 Ì !™Ú. ¨5éù ½é 40(”ýv ”¡ 28)÷¿ Ùâ uú ½ !™ °
ü‰ùé°.
dT
(i)r(i) = uT
i r(i). (42)
[”¡ 28] Ò• “³ d(0)® d(1) ¯â u0, u1õ Ì Š §0q€÷t¿, 0ù ô¢ ÙÛ‡¢ D2(ç• –‹)õ
f¢°. ¡ò¨ e(2)™ D2‚ A-”pT, #4“(residual) r(2)™ D2® ”p°. °ü ŠÄú æ« ”¿Ï Ò• “³
d(2)ù“š«“¦Ò•“³¯â0¿fü™ÙÛ‡¢D2‚A-”p êÀ(u2õÌ Š) §0q•°. d(2)õf£
Xu2õ “v”Š-Ùy!ŠªÜõXÌ Šf ŸX‘‚, d(2)®u2¦b0ùD2‚e±¢eV‚nŠ!°.
`ú )÷Vt ¢ “ Ì s›£ Dù /Â Ÿªú €Ì£ X® ¥ô “¿ Šª “³ Ÿª
‹è ±µ-¯â … Ÿ ƒú ŠÄ èŸ¥° ¢ ¥§ êÀ £ ½ !°™ b°. õ æ©t™ 54
“(residual)úqƒ£X°ü‰ùbÜéú€Ì Š˜¢°.
r(i+1) = −Ae(i+1)
= −A(e(i) + α(i)d(i)
= r(i) − α(i)Ad(i) (43)
8 ŠŠŠªªªiiiPPPêêê(conjugate gradient) ŸŸŸªªª
Šª i€ê Ÿªú °Ø™ ˜‚t Šª i€ê Ÿª‚ Â¢ RÌ “š«“ê s›ü“ w™ D ’£
D“§, ›Å¢c(6X g@€°. €ìŠªi€êŸª†™DùŠª“³Ÿª‰ô¢Ú,
³“Ò•“³ú§0X54“(residual)õŠªÜ Š§(°™D°(Œ, ui = r(i)¿ze¢°).
39

4
X)- –{†
, ‡ô‘‡
, î–|††
, êõ‡‡
b
¢ xØ “ªù Š² “ î¿ ¦ýX°. Íx /Â Ÿª‚t 54“(residual)ú €Ì ™
D 0 ô°÷¦ Šª i€ê Ÿª‚t™ €Ì “ q£ î {°. ¦«, 54“(residual)ù Y¦ Ò
• ¯â® ”p¢°™ ”ù 4ú “v !°(½é 39). H†t 54“(residual) ¯â 0¯â s¦†V
¨’Y¦Ò•“³‚xÍë¢”Ò•“³úf£½ !°. 54“¯â 0 ¯âiÍ™”%
¿© uq•iÍt¿‘g ü“w™°. 5|‚ÃQüW“§, 54“(residual)ú€Ì ™Ú‚™
ÌÎ¦ýXî …8¢°.
54“ ¯âõ €Ì ™ D qi ¦yõ “™“ f¡© Ã%. Ò• ¯â0 54“(residual)ú Ì
Š§0q“ŸX‘‚, 54“¯â0f ™ÙÛ‡¢, Œspan{r(0), r(1), · · · , r(i−1)}ùDi®ô
°. ¢ ¡¡¦ 54“(residual)™ Y B• “³‰ ”pt¿ Y¦ 54“ ¯â c£®ê ‹è ”p¢
°((”¡29 ÷ƒ). H†t½é41ù°ü‰°èvÇý°.
rT
(i)r(j) = 0, i = j (44)
43‚t0y¿Ï€ìù¡¡¦”54“(residual) r(i) Y54“(residual)®Ad(i−1)¦xÍƒ¦
†™D°. d(i−1) ∈ Diú’Ÿ V, €ìùdv¡¡¦”¿ÏÙÛ‡¢Di+1YÙÛ‡¢Di®
ÙÛ‡¢ADi¦¦÷¿ÙâÍý°™D°.
D(i) = span{d(0), Ad(0), A2
d(0), · · · , Ai−1
d(0)}
= span{r(0), Ar(0), A2
r(0), · · · , Ai−1
r(0)}.
ÙÛ‡¢ú¾ ¿’ÙÛ‡¢(Krylov subspace)†v ™Ú, Dù 5¦¯â‚qi±µúŠ
ÄX÷¿XÌ Šf£½!°. ‡¢ù Í”ù4ú “v!°: ADi Di+1‚j¥üq!v,
°ü54“ri+1‰Di+1‰”p t¿(½é39), ri+1Di‰A-”põÚ°™€ìúx½!°. ri+1
d(i)õg½¢Y¦c(Ò•“³‰yA-”põØv!ŸX‘‚”Š-Ùy3dªÜz¢³©
“™D°!
½é37‚5Í5™”Š-Ùy3’½ βij = −uT
i Ad(j)/dT
(j)Ad(j)ú’Ÿ %; éú¢œ Q§0
qÃ%. Íx½é43‰riúRX V°ü‰ùd‰õu™°.
40

4
X)- –{†
, ‡ô‘‡
, î–|††
, êõ‡‡
b
[”¡29] Šªi€êŸª‚t, ³q‚t”¿u©“™#4“(residual)™Y¦³q‚t#Í.Ï#4“(residual)
ˆ£‚Â Š”pT, ”ÄQxØü™Ò•“³ùY¦c(#4“®Ò•“³‚Â©A-”p üêÀ§0q•°.
(Ò• “³ù #4“ ¯âõ Ì Š §(°). r(2)® d(2)¦ bù D(2)(q¨Q ”²• ÙÛ‡¢)® e±¢ eV‚ nŠ
!°. Šªi€êŸª‚td(2)™r(2)®d(1)¦xÍƒ¦°.
rT
(i)r(j+1) = rT
(i)r(j) − α(j)rT
(i)Ad(j)
α(j)rT
(i)Ad(j) = rT
(i)r(j) − rT
(i)r(j+1)
rT
(i)Ad(j) =



1
α(i)
rT
(i)r(i), i = j,
−1
α(i−1)
rT
(i)r(i), i = j + 1, (é44‚¦ Š)
0, ”½¦iÍ.
∴ βij =



1
α(i−1)
rT
(i)r(i)
dT
(i−1)
Ad(i−1)
, i = j + 1
0, i j + 1, (é37‚¦ Š.)
¥Á

¤ÂÙÛ¦βij ¨ù€†u£¹°. g”¿Ï¯â A-”p üêÀ Ÿæ©Ì’Y
‚€Ì°ÏÒ•¯âúc£õW6£›Å {°. ¢|Å¢6bŠªi€êŸª¦|Å¢b
T, ŠÄè‡¢Ä3ê®è¢Ä3êV‚tO(n2
)‚tO(m)¿§™ý°. XmùA¦0s¨Û¦
½°. gÙâ5™β(i) = βi,i−1¦9™Í÷¿vŸ£D°. ˆÌ¢œ8§0V°ü‰°.
β(i) =
rT
(i)r(i)
dT
(i−1)r(i−1)
(½é32‚¦ Š)
=
rT
(i)r(i)
rT
(i−1)r(i−1)
(½é42‚¦ Š)
g“š«“z`¢RÌc£cs 5¿eý©Ã%. Šªi€êŸªˆ°ü‰°.
41

4
X)- –{†
, ‡ô‘‡
, î–|††
, êõ‡‡
b
[”¡30] Šªi€êŸª
d(0) = r(0) = b − Ax(0), (45)
α(i) =
rT
(i)r(i)
dT
(i)Ad(i)
(½é32®42‚¦ Š) (46)
x(i+1) = x(i) + α(i)d(i), (47)
r(i+1) = r(i) − α(i)d(i),
β(i+1) =
rT
(i+1)r(i+1)
rT
(i)r(i)
(48)
d(i+1) = r(i+1) + β(i+1)d(i) (49)
”¡ 30ù Šª i€ê Ÿªú Íý €Ì v !™ šg‚ XÌ°ú X¦ uQ ü™ ú ÃŠs
v !°. €ì Ÿª‚t 5Í5™ ŸÐŸ(gradient)™ t¿ Šª s¦Ÿ X‘‚ “Šª i€ê(conjugate
gradient)”†™Ìq™°™0qýD†v£½!°. ŸªùŸÐŸõŠªÜ ŠÒ•“³úuŸX
‘‚“ŠªÜýŸÐŸ(conjugated gradient)” Ÿª†v ™DÌeÝ¢vÇ°.
9 ŠŠŠªªªiiiPPPêêê¦¦¦½½½¶¶¶ÛÛÛuuu
Šª i€ê™ n ¥¦ ŠÄ ó‚ °Òý°. ”©°V Šª i€ê Ÿª¦ ½¶ Ûu‚ · ‘îú £q˜ £
42

4
X)- –{†
, ‡ô‘‡
, î–|††
, êõ‡‡
b
«? ìg¿ Ÿªú XÌ V Ùô™½b Š¤¡ ¡ò X‘‚ 54“(residual) bb ÙeÝ©“T, £¡
¡ò(cancellation error) X‘‚Ò•¯â0€¦A-”pbb’ìý°. Š¤¡¡ò‚¦¢‘g™/
Â Ÿª‚t©d¢†®°Û½!“§, £¡¡ò‚¦¢‘g™ÖQ©d£½!™‘g s
¦°.

¤¡ò‚¦©Ò•¯â0€¦Šª·q“™‘gX‘‚1960‘Â @X«“½¡
q™Šªi€êŸª‚‘îú£“w…÷T, 1970‘Â‚0qtŠÄú ©©õu ™“ª÷¿¦
Šªi€êŸªî‰X†™d‰ Œvýó‚˜ü¿t°è‘îú‹Qý°.
è¢% Šªi€ê‚Â¢b©êº°°. ¡š@Šªi€ê ìg¿XÌü™‘g™”¾Ÿ
gˆ5vtn ¥¦ŠÄ½±Ý ¢iÍ ÂÙÛŸX‘‚, ½¶Ûu|Å¢¦yõ •°. ½
¶ÛuùÙô™½b¡òõ¦Ÿæ¢Ds5†, eÝ¢xvý÷¿©d£½{™‘g0‚Â©Š
ªi€êŸªîÌ °™bú’` Ÿæ¢D°.
Šªi€êŸª¦¥«ŠÄ³q™/Â Ÿª¦¥«ŠÄ³q®ô °. H†t6.1 `
¦RÌú”Â¿Ì ŠŠªi€êŸª³¢¥¦ŠÄ§‚½¶ ™ƒ8úz`£½!°.
9.1 °°°¹¹¹¢¢¢°°°¨¨¨ééévvvòòòŸŸŸ
Šªi€êŸª¦¡³q‚t, ©e(i)™e(0) + Di¿ÙâxØüv, XDi™°ü‰ùÙÛ‡¢ú
y…•Ã…°.
Di = span{r(0), Ar(0), A2
r(0), · · · , Ai−1
r(0)}
= span{Ae(0), A2
e(0), A3
e(0), · · · , Ai
e(0)}.
®ù¾ ¿’(Krylov) ÙÛ‡¢ù¢ “ŸÛ”ù4ú •°. veýi‚Â©, ¡ò¨ù°
ü‰vÇý°.
e(0) =

I +
i
j=1
ψjAj

 e(0)
q½ ψj™ © α(i), β(i)® ‘qüT, eÝ¢ ‘qù ŠŸt |Å “ w°. |Å¢ Dù 7.3‚ 5® !™
’`, Œ, Šªi€êŸª||e(i)||Aõ/™Ü ™q½ψjõxØ¢°™€ì°.
æ é‚t ’Òu¦ vÇù °¨é÷¿ vÇþ ½ !°. Pi(λ)õ ò½ i¦ °¨é† %. Più %
¿ ©5 ±µ ¤ ½ !÷T, 0ù ô Q qƒý°. šõ 0q, § P2(λ) = 2λ2
+ 1†v V,
P2(A) = 2A2
+ I ý°. ¢õ !™vŸªùPi(A)v = Pi(λ)v(Av = λv, A2
v = λ2
v, · · · .)®
vî¯â‚tîÌ °.
§Pi(0) = 1üêÀ ²v V, ¡ò¨ù°ü‰vÇþ½!°.
e(i) = Pi(A)e(0),
43

4
X)- –{†
, ‡ô‘‡
, î–|††
, êõ‡‡
b
Šªi€êŸªùψj q½õxØ£X, °¨éúxØ¢°. °¨éúe(0)‚XÌ£X¦î‰‚Â©
ƒ€ %. /Â Ÿª¦Ûu‚t®¥ô “¿, e(0)õ”p³ævî¯â0¦xÍƒ¦÷¿vÇ¢°.
e(0) =
n
j=1
ξjvj,
”ýv°ü¦é0úqU½!°.
e(i) =
j
ξjPi(λj)vj
Ae(i) =
j
ξjPi(λj)λjvj
e(i)
2
A =
j
ξ2
j [Pi(λj)]2
λj.
Šª i€ê Ÿªù vÇéú /™Ü ™ °¨éú ü÷T, “ª¦ ½¶ šê™ sˆý ”sê /t
¦ vî¯â ½¶ ™ eêÃ° ”ú ½ {°. Λ(A) A¦ vî©0¦ š¦† V ¡ò¦ ‚g“
i(norm)ù°ü‰°.
e(i)
2
A ≤ min
Pi
max
λ∈Λ(A)
[Pi(λ)]2
j
ξ2
j λj
= min
Pi
max
λ∈Λ(A)
[Pi(λ)]2
e(0)
2
A (50)
”¡31ù vî© 2® 7ú “™ šg‚ Â© æ¦ vÇéú /™Ü ™ °¨éú a “ ‘ê¦ ò
½‚ Â© ÃŠsv !°. P0(0) = 1ú §„ ™ ò½ 0¦ °¨éù 5 ˆ‚ {÷T, ™ 31(a)‚t Ã
™ †® P0(λ) = 1°. ò½ 1¦ /X °¨éù P1(λ) = 1 − 2x/9v, ”¡31(b)‚t Ç ½ !°.
P1(2) = 5/9, P1(7) = −5/9v, Šª i€ê¦ ¥« ŠÄ ó ¡ò¨¦ ‚g“i #ŸX 5/9Ã° ¾
“wüúx½!°. ”¡31(c)™£¥¦ŠÄóé50¦d‰ 0ÿúÃŠu°. Dù2ò°¨éƒ
b(P2(0) = 1, P2(2) = 0, P2(7) = 0)ú“5êÀ£½!ŸX‘°. ŠX÷¿ò½n¦°¨éùn +1¦
b0ú“5¿À§0½!÷t¿n¦t¿°ôvî©0ú½Ì£½!°.
“š«“¦ f¦õ © Šªi€êŸª n¥¦ ŠÄó‚ eÝ¢ d‰õ u™°™ Dú Ì 0 x ½ !
°: ÌÍŸ ù vî©0 …8¢°V Šªi€êŸª Ì §òQ ½¶¢°™ D‚ Â¢ ’`°. ˆ¢
½u¦Ùô™½be}êõ •°v£X, eÝ¢©õqƒ Ÿæ©Åuü™ŠÄì½™ŸÊ©˜t¿
°ôvî©0¦½ ý°. (ô‘Ò‚Â¢¢ “°ô !°: x(0) A¦Ùvî¯â0‰
yA−”põØv!™iÍ°. §™x(0)õY£X5Í5“w™vî¯â0ù”‚©¾ ™vî
©0‹èé50‚5Í5“wúD°. ” 5ˆtiv¢†®, ¢vî¯â0‹èÙô™½
bŠ¤¡¡ò‚¦©°è5Í5QþD°.)
44

4
X)- –{†
, ‡ô‘‡
, î–|††
, êõ‡‡
b
[”¡ 31] i¥¦ ŠÄú ½±¢ ó Šª i€ê Ÿª v¥# ½¶°™“™ Pi(0) = 1†™ sq• g¢ ƒ8‚t i ò
°¨éPi ¡¡vî©‚tv¥#0‚ «Ï“‚µ²!°.
vî©0 λmin‰ λmax €‚ Ý‘Y Q Ûjüq !™ DÃ°, ”¡31(d)® –

‚ cŠ !™
iÍŠªi€êŸªÌÎý½·£½!üúx½!°. DùŠªi€êŸª‚té50¦©ú
Q§™°¨éúxØ ™DÌÎÑq“ŸX‘°.
§±µA¦vî©0¦4úxv!°V§ô½¶úqR™°¨éúgu£½ê!“§, Š
Ÿt™ 6ŠXiÍ, Œvî©0λmin‰λmax €‚vòQÛj v, |Äü™vî©¦½ X
q¨ù½¦t¿°ôvî©5Í5T, Ùô™½bŠ¤¡¡ò Œf ™iÍõ e¢°.
9.2 üüüËËË’’’(Chebyshev) °°°¨¨¨ééé
¢ “ îÌ¢ c–“ªù î¢ ¦ b‚ Â©t s¦† ©æ[λmin, λmax]‚t é50ú /™Ü ™ D
°. õ½±£½!™°¨é0ùüË’(Chebyshev) °¨éúŸŠ÷¿¢°.
ò½i¦üË’(Chebyshev) °¨éù°ü‰°.
Ti(ω) =
1
2
[(ω + ω2 − 1)i
+ (ω − ω2 − 1)i
].
(é°¨é

¤Ã“w™°V, i 152iÍ‚Â©qÃ†.) a “üË’(Chebyshev) °
¨é0 ”¡32‚ ”²u !°. üË’(Chebyshev) °¨é0ù e¦‹ ω ∈ [−1, 1]‚t |Ti(ω) ≤ 1| 4
ú “T(€ì-1‰1¦€‚t•ô¢°), c(°¨é‚!qt|Ti(ω)|¦©ùω /∈ [−1, 1]e¦‹‚
45

4
X)- –{†
, ‡ô‘‡
, î–|††
, êõ‡‡
b
[”¡32] ò½2, 5, 10, 49¦üË’(Chebyshev) °¨é0
t/ÂXõQý°. y} “wùvÇ÷¿˜Ÿ V, |Ti(ω)|¦©”¡‚5Í5!™’%¦ˆ‚
t ¢¢ 6§òQ’ ¢°.
½é50°ü‰ùPi(λ)õxØ¥‚¦©/™Üü™DùÙÀC3‚tz`ý°.
Pi(λ) =
Ti(λmax+λmin−2λ
λmax−λmin
)
Ti(λmax+λmin
λmax−λmin )
°¨éù –‹ λmin ≤ λ ≤ λmax‚t üË’(Chebyshev) °¨é¦ •ô 4ú •°(”¡33 ÷ƒ).
Ûc™ Pi(0) = 1†™ Åu€¨ú ?„ Q T, Û%™ λmin‰ λmax €¦ u¢‚t /Â© 1ú •
°. H†té50÷¿Ùâ°ü¦é¢¢°.
e(i) A ≤ Ti
λmax + λmin
λmax − λmin
−1
e(0) A
= Ti
κ + 1
κ − 1
−1
e(0) A
= 2
√
κ + 1
√
κ − 1
i
+
√
κ − 1
√
κ + 1
i −1
e(0) A. (51)
€¡Í’Òu¦£¥« ½(¤Õ, addend)™i ’ ¥‚H†0÷¿½¶¢°. H†tŠªi€ê¦½¶
ùˆÌ™¢Ù5é÷¿°ü‰vÇ ™DŠX°.
e(i) A ≤ 2
√
κ − 1
√
κ + 1
i
e(0) A (52)
46

4
X)- –{†
, ‡ô‘‡
, î–|††
, êõ‡‡
b
[”¡ 33] ŠX iÍ‚t –‹ λmin = 2® λmax = 7‚t é 50ú /™Ü ™ °¨é P2(λ). wxù ò½ 2¦
Chebyshev °¨é¦ ¾Ÿõ ºÍ¢ D°. £ ¥¦ ŠÄ ó¦ ¡ò¨¦ ‚C“ i(norm)ù #Ÿ©¦ 0.183•õ J“
M™°. 2¦vî©§…8 ™D÷¿yN²u!Ï”¡31(c)®üp †.
Šªi€ê¦¥«³q™/Â ¦¥«³q®ô °. é51‚ti = 1¿£V, /Â ‚‘
¢½¶d‰é28úu™°. Dù”¡31(b)‚”²•xÍ°¨é¦iÍ°.
”¡34™Šªi€ê¦ŠÄ¥°¦½¶‚Â¢êv°. ìg¿XÌ°úX, Šªi€ê™”ùvî
©Ûj5”ùèæX5¦îX‘‚Â¦iÍé52 è€ ™½¶šêÃ°Ì§òQ½¶¢°.
é52®é28úüp V, Šªi€ê(conjugate gradient) Ÿª/Â (steepest descent) ŸªÃ°Ì§
òQ½¶ ™°™D`Ý °(”¡35 ÷ƒ). ” 5Šªi€ê¦c(ŠÄ³q /Â ŸªÃ°
Ì §òQ ½¶ ™ Dù s¦°; šõ 0V, Šª i€ê Ÿª¦ ¥« ³q™ /Â Ÿª¦ ¥« ³
q®ô °. é52‚t…©u!™½2‚¦©tŠªi€êŸªÙŠÄ³q‚t™¢¦šêW
õÃ½!Qý°.
10 ÄÄÄ333êêê
/Â 5Šªi€êŸª¦¡³q‚t 6¨ùqƒè¢ú›Å¿ ™ƒù±µ-¯â…‡°.
ŠX÷¿, ±µ-¯â…‡ù±µ¦0s¨Ù™¦½õm†£iÍO(m)¦qƒè¢ú›Å¿¢°.
‘t¦1 `‚t5Žý°j¢‘g0‚tÃ A™2™±µvm ∈ O(n)°.
ε¦•½¿¡ò¦¾ŸõvŸæ©?Û¢ŠÄú½± ŸõÙ¢°v e %: Œ, e(i) ≤ ε e(0) .
47

4
X)- –{†
, ‡ô‘‡
, î–|††
, êõ‡‡
b
[”¡34] ’×½¦¥½¿t¦Šªi€ê(ŠÄ¥°)¦½¶. ”¡20‰üp †.
é28ù/Â Ÿªú€Ì Š¢qõ§„ Ÿæ©Åuü™/Â¦ŠÄì½ °ü‰üúÃ
Šu°.
i ≤
1
2
κ ln
1
,
¢–, é52‚¦ VŠªi€êŸªÅu ™/Â¦ŠÄì½ °ü‰°.
i ≤
1
2
√
κ ln
2
.
/Â ùO(mκ)¦è¢Ä3êõ “T, Šªi€ê™O(m
√
κ)¦è¢Ä3êõ •°™dÁ°. £
xvýc£‡¢Ä3ê™O(m)°.
d−òÙ e¦‹‚t ò ÍÙ iq© ‘g0ú î¢òÛ‰ î¢Å™ª÷¿ –€£ X¦ Ä3ê™ ‘‘
κ ∈ O(n2/d
) ý°. H†t, /Â Ÿªù òÙ ‘g0‚ Â© O(n2
)¦ è¢Ä3êõ ““§ Š
ªi€ê™O(n3/2
)°. ¢ˆòÙ‘g0‚Â©/Â ùO(n5/3
)¦Ä3ê“§Šªi€êŸªù
O(n4/3
)¦è¢Ä3êõ •°.
11 èèè‰‰‰‘‘‘ÒÒÒ
ˆtz`¢/Â ‰Šªi€êxvý‚t, a “ƒÙXD0fœü}°; 48, èbúqx
QxØ vsg‘Ò —a¦‘g°.
48

4
X)- –{†
, ‡ô‘‡
, î–|††
, êõ‡‡
b
[”¡35] Šªi€ê¦¢¥¦ŠÄ‚X Ÿæ©Åuü™/Â ¦ŠÄì½.
11.1 èèè
è‚‘ Šz`£Dù¨“w°. §x¦©‚Â©ÂœX8eX !°V, ”Dúè©x(0)¿
€Ì †. ”©“w°V, x(0) = 0÷¿£q†; xÍèßðú{™iÍ/Â 5Šªi€êŸªùd
v ½¶ Q üq !°. üxÍ /™Ü(14 `‚t z`)™ Š ¦ “‹/™ …8£ ½ !v è æX¦
xØ‚H†q—/™b‚½¶£“ deüT, qiiÍ‚™½¶Øq—“”©“wú“õde
ŸX‘‚«°¿Ï‘g ý°.
11.2 ‘‘‘ÒÒÒ
/Â 5Šªi€ê /™b‚êµ£X54“(residual)™0üv, §é11548ó¦¢
¥¦ŠÄúÌ Q¢°V, Ûc 0ý°. H†t54“(residual)0üVŒèqƒ‘Òüq˜¢
°. 54“(residual)¦ bÜé Í×(47) qƒ‚t Š¤¡ ¡ò €Xü™ iÍ‚™ 54“ 0 s¨Úê
0÷¿qƒþ½ !°; ‘g™é45õÌ Šqƒú”¿è¥÷¿t©dþ½!°.
Ã ¦iÍ½¶°Y8Øq“ŸY‚xvý‘ÒüŸõÙ¢°. ¡ò¨úÌ£½{ŸX
‘‚ 54“(residual)¦ ¾Ÿ €Y‚ `èý © ¿ R² V ‘Ò ™ D Ã °; ‘‘ ©÷¿
#Ÿ54“(residual) ©‚0Ã°ù©εú…©uùù©ú€Ì¢°. ( r(i) ε r(0) ). šg‘™
ÙÀB‚tÇ½!°.
49

4
X)- –{†
, ‡ô‘‡
, î–|††
, êõ‡‡
b
12 YYY

ý™±µ¦ƒ8½(condition number)õx Ÿæ¢Ÿª°. ±µM±µAõ–€ ™Âa
Vtj¦eÙÒ±µv, ‹±µúÖQqƒ£½!°v %. ”©°V°üéúqt¢cX÷¿
Ax = bõ½!°.
M−1
Ax = M−1
b. (53)
§κ(M−1
A) κ(A)65M−1
A¦vî©0A¦vî©0Ã°Ì0cŠ!°V, Ù’¦‘gÃ°
é53¦‘g ŠÄªú ©Ì0½¶¢°. ‘g™±µM5A Âavj¦eÙÒ±µ†
Ì†ê±µM−1
AùŠX÷¿”©“w°™D°.
ÂaTj¦eÙÒc(±µM‚Â©EET
= M4ú “™±µE (î¢Dùs¦“
§) …8 ŸX‘‚, q²Óù˜£½!°. (”¢±µE™ªßÅ(Cholesky) Û©®ù“ª÷¿u
£½!°.) ±µM−1
A®E−1
AE−T
™ô¢vî©0ú •°. D¢ ™î™v vî©λõ
“™±µM−1
A¦vî¯âX, ET
v™°ü‰vî©λõ “™±µE−1
AE−T
¦vî¯â
ŸX‘°.
(E−1
AE−T
)(ET
v) = (ET
E−T
)E−1
Av = ET
M−1
Av = λET
v.
xÍèßðAx = b™°ü¦‘g¿ºÍþ½!°.
E−1
AE−T
x = E−1
b, x = ET
x,
‘g‚tÍý™Íxx‚Â©v5tx‚Â©}°. ±µE−1
AE−T
ÂaVtj¦eÙÒŸ
X‘‚, x™ /Â 5 Šªi€ê‚ ¦© u£ ½ !°. Šª i€ê Ÿªú €Ì Š ‘gõ ©d
™‰eú“ºÞýY

ýŠªi€êŸª(Transformed preconditioned conjugate gradient method)”†Ùô
°.
d(0) = r(0) = E−1
b − E−1
AET
x(0),
α(i) =
rT
(i)r(i)
dT
(i)E−1AE−T d(i)
,
x(i+1) = x(i) + α(i)d(i),
r(i+1) = r(i) − α(i)E−1
AE−T
d(i),
β(i+1) =
rT
(i+1)r(i+1)
rT
(i)r(i)
,
d(i+1) = r(i+1) + β(i+1)d(i).
50

고뇌의 고통이 없는 켤레 경사도 기법 개론(1과 1/4판)

More Related Content

What's hot

Viewers also liked

Similar to 고뇌의 고통이 없는 켤레 경사도 기법 개론(1과 1/4판)

More from Changwon National University

Recently uploaded

고뇌의 고통이 없는 켤레 경사도 기법 개론(1과 1/4판)