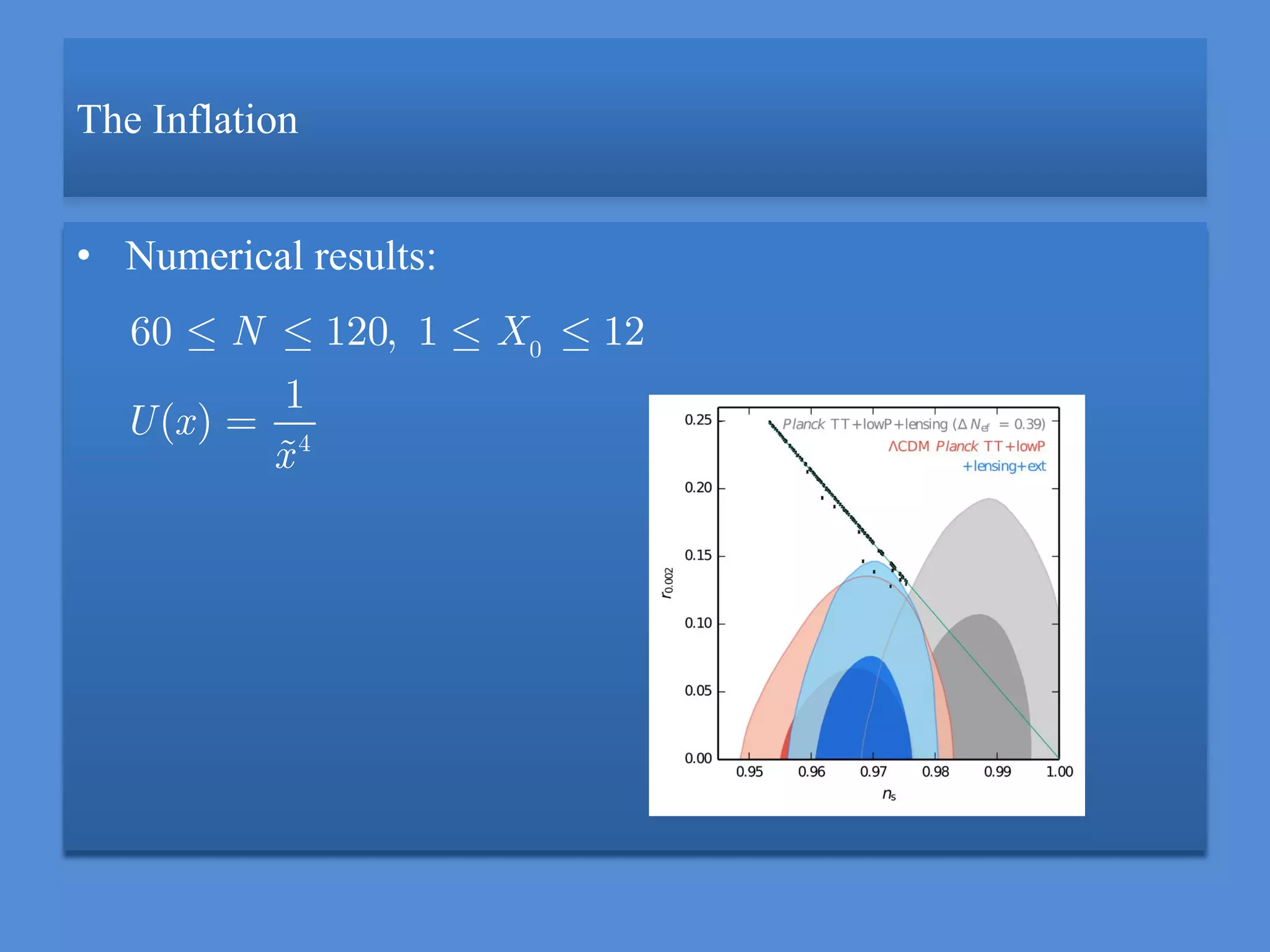
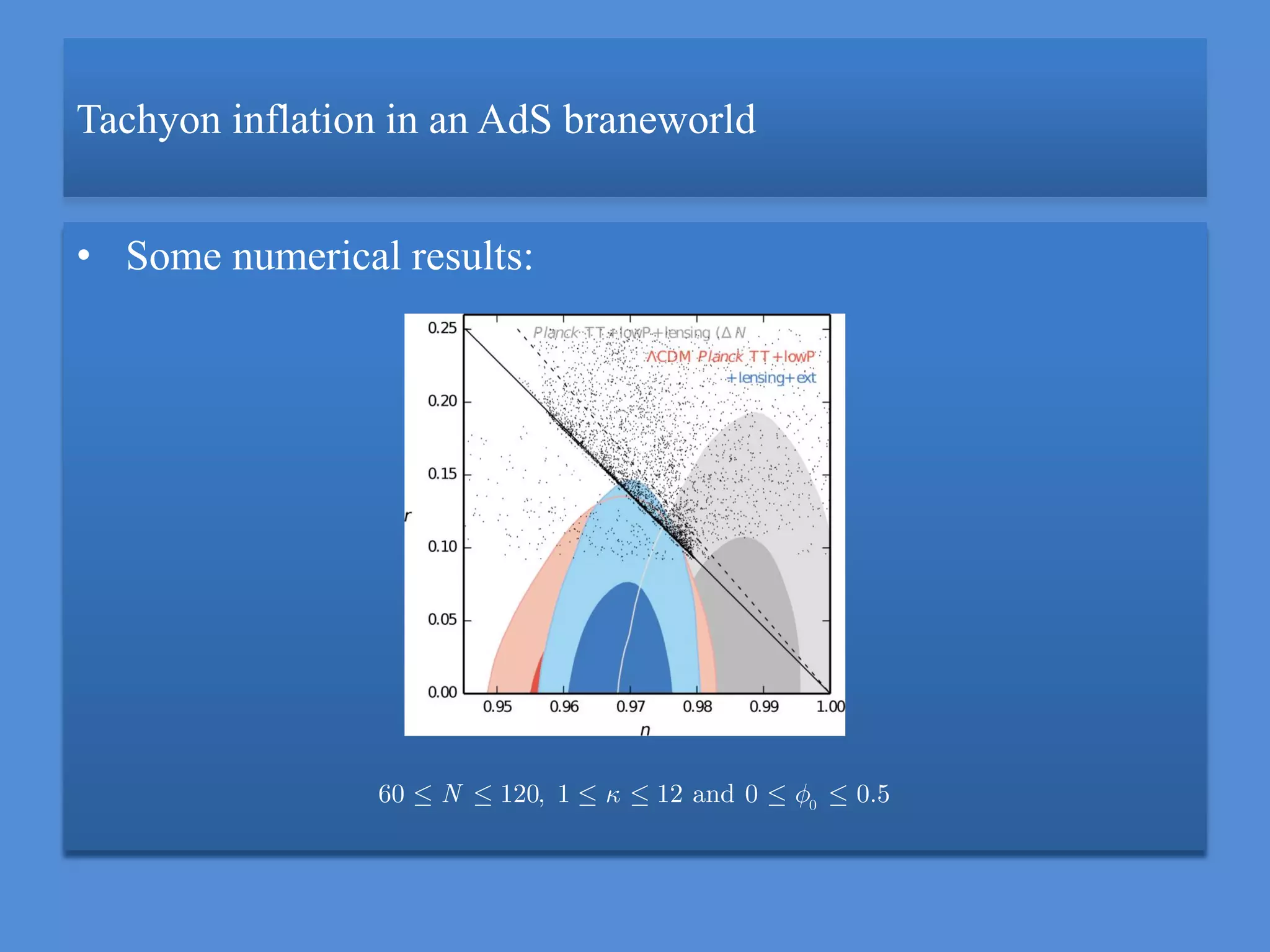
This document summarizes research on tachyon inflation in an anti-de Sitter (AdS) braneworld framework. The researchers study a tachyon field on a dynamical 3-brane embedded in a 5-dimensional AdS bulk spacetime. They derive the equations of motion for the tachyon field and radion field in this braneworld cosmology. Dimensionless equations are obtained and numerical results show that the model can produce over 60 e-folds of inflation with observable parameters consistent with current data. The analysis provides a novel mechanism for tachyon inflation distinct from standard 4D models, with predictions depending on only one free parameter related to the AdS curvature scale.

1. Dragoljub D. Dimitrijevic, Neven Bilic,
Goran Djordjevic, and Milan Milosevic
FSM, University of Nis, Serbia and RBI, Zagreb, Croatia
Tachyon Inflation in the RSII
Framework
SEENET-MTP Balkan Workshop BW2018:
Field Theory and the Early Universe
June 10-14, 2018, Niš, Serbia

2. 1 Introduction
2 Tachyon field cosmology
3 Tachyon inflation in an AdS braneworld
4 Final remarks

3. Introduction
• We study (real) scalar field in cosmological context.
• General Lagrangian action:
• Lagrangian (Lagrangian density) of the standard form:
• Non-standard Lagrangian:
( , ) ( ) 1 2 ( )tach T X V T X T   
( , ) ( ) ( )X V      
4
( ( ), )S d x g X    
1
2
X g T T
   

4. Introduction
• The action:
• In cosmology, scalar fields can be connected with a perfect
fluid which describes (dominant) matter in the Universe.
• Components of the energy-momentum tensor:
4
( , )S d x g X T 
2 S
T
gg
 


 

( )T P u u Pg     

5. Introduction
• Pressure, matter density and velocity 4-vector, respectively:
( , ) ( , )P X T X T
( , ) 2 ( , )X T X X T
X


 

2
T
u
X




( )T P u u Pg     

6. Introduction
• Total action: term which describes gravity (Ricci scalar,
Einstein-Hilbert action) plus term that describes cosmological
fluid (scalar field Lagrangian):
• Einstein equations:
 4
( , )S d x g R X T  
1
2
R Rg T   

7. Tachyon field cosmology
• Tachyon lagrangian:
• EoM:
( , ) ( ) 1tach T X V T g T T
     
2
2
1
(1 ( ) )
1 ( ) ( )
T T dV
g T T T
T V T dT
 

 
  
       
  

8. Tachyon field cosmology
• Tachyon lagrangian:
• Friedmann equations for spatially homogenous scalar field:
2
2
2 2 1/2
1
3 (1 )Pl
a V
H
a M T
( , ) ( ) 1tach T X V T g T T
     
2
3 0
1
T V
HT
VT

9. Tachyon field cosmology
• Rescaling:
• EoM:
• Hubble parameter rescaling:
0
T
x
T 0
1 ( )
( )
T V x
U x V
T 0
t
t
3 2
0
'( ) '( )
3 3 0
( ) ( )o
U x U x
x HT x x HT x
U x U x
0
H T H

10. Tachyon field cosmology
• Dimensionless equations:
2
2 0
2
2
2 3/2
0
( )
3 1
(1 ) ( )
3 ( )(1 ) 0
( )
X U x
H
x
x dU x
x X U x x x
U x dx
2 4
0
0 2 3
,
(2 )
s
Pl s
T M
X
M g

11. The Inflation
• Slow-roll regime, slow-roll parameters:
• Number of e-folds:
*
1 0
ln | |
, 0,i
i
d H
i
dN H
1 2 12
2
1 2
1
, 2
3
, 2
2
H H
H HH
x
x
Hx
( ) ( )
e
i
t
t
N t H t dt

12. The Inflation
• Number of e-folds:
• The scalar spectral index:
• The tensor-to-scalar ratio:
2
2
0 1
( )
( ) , where ( ) 1
| ( ) |
e
i
x
e
x
U x
N x X dx x
U x
1
16 ( )i
r x
1 2
1 2 ( ) ( )s i i
n x x

13. The Inflation
• Numerical results:
0
4
60 120, 1 12
1
( )
N X
U x
x

14. Tachyon inflation in an AdS braneworld
• Randall–Sundrum models (1999) imagine that the real world
is a higher-dimensional universe described by warped
geometry. More concretely, our universe is a five-dimensional
anti-de Sitter space and the elementary particles except for the
graviton are localized on a (3+1)-dimensional brane(s).
• A simple cosmological model of this kind is based on the RSII
model.

15. Tachyon inflation in an AdS braneworld
• Cosmology on the brane is obtained by allowing the brane to
move in the bulk. Equivalently, the brane is kept fixed at z=0
while making the metric in the bulk time dependent.
• The fluctuation of the interbrane distance implies the existence
of the radion.
• Radion – a massless scalar field that causes a distortion of the
bulk geometry.

16. Tachyon inflation in an AdS braneworld
• The bulk spacetime of the extended RSII model in Fefferman-
Graham coordinates is described by the metric
• Inverse of the AdS curvature radius – k
• Radion field –
• Fifth coordinate – z
 
 
2 2 2 2
(5) 22 2 2 2
1 1
1 ( )
1 ( )
a b
abds G dX dX k z x g dx dx dz
k z k z x
  


 
    
  
( )x

17. Tachyon inflation in an AdS braneworld
• Add dynamical 3-brane, i.e. tachyon field (in terms of induced
metric).
• The action, after integrating out fifth coordinate z:
• Radion field (canonical) –
• Tachyon field –
, ,4 4 2 2 2
, , 4 4 2 2 3
1
(1 ) 1
16 2 (1 )
gR
S d x g g d x g k
G k k

 
 


 
  
           
    


 2
sinh 4 / 3 G  

18. Tachyon inflation in an AdS braneworld
• In the absence of radion – tachyon condenzate:
• Going back, lagrangian we are playing with:
(0) 4
br , ,4
1S d x g g
2 2
1 k   
2
, ,
, , 4 3
1
1
2
g
g

 
 


 
    


19. Tachyon inflation in an AdS braneworld
• Hubble expansion rate H in standard cosmology (without
brane):
• Hubble expansion rate H in RS cosmology:
8
3
a G
H
a

 
2
8 2
1
3 3
a G G
H
a k
  
   
 

20. Tachyon inflation in an AdS braneworld
• Hamilton’s equation:
3
3
H
H

21. Tachyon inflation in an AdS braneworld
• Dimensionless:
2 4
/ , / ( ),
/ ( )), , / ( )
h H k k
k k k
4
8 2
8 2
2 8 2
10 2
5 8 2
1 /
4 3 /
3
2 1 /
4 3 /
3
1 /
h
h




 


 

 
 

  
  
  
   
  
 
   




  


  

2 2
( ) 1
2 6
h p
N h
 
 
 
    
 

2 2
8 Gk 

22. Tachyon inflation in an AdS braneworld
• Slow-roll parameters:
• Observational parameters:
1 i 1 i 2 i
2
s 1 i 2 i 1 i 1 i 2 i 2 i 3 i
1
16 ( ) 1 ( ) ( )
6
8
1 2 ( ) ( ) 2 ( ) 2 ( ) ( ) ( ) ( )
3
r C
n C C
  
      
 
    
  
        
  
22 2 2
1 2 4 4
2 12 2 2 2 2
2 2 4 4 4 4
8
1 1
6 12
8
1 1 1
12 4 6 6

23. Tachyon inflation in an AdS braneworld
• Some numerical results:
0
60 120, 1 12 and 0 0.5N

24. Final remarks
• The ns/r relation here is substantially different from the
standard one and is closer to the best observational value.
• The model is based on the brane dynamics which results in a
definite potential with one free parameter only.
• We have analized the simplest tachyon model. In principle, the
same mechanism could lead to a more general tachyon
potential if the AdS5 background metric is deformed by the
presence of matter in the bulk.

25. References
• N. Bilic, D.D. Dimitrijevic, G.S. Djordjevic and M. Milosevic, Int. J. Mod.
Phys. A32, 1750039 (2017).
• D.A. Steer and F. Vernizzi, Phys. Rev. D 70, 043527 (2004).
• A. Sen, JHEP 04, 048 (2002).
• L. Randall and R. Sundrum, Phys. Rev. Lett. 83, 4690 (1999).
• G.S. Djordjevic, D.D. Dimitrijevic and M. Milosevic, Rom. Rep. Phys. 68, No.
1, 1 (2016).
• M. Milosevic, D.D. Dimitrijevic, G.S. Djordjevic, M.D. Stojanovic, Serb.
Astron. J. 192, 1-8 (2016).
• N. Bilic, D.D. Dimitrijevic, G.S. Djordjevic, M. Milosevic, M. Stojanovic, AIP
Conf. Proc. 1722, 050002 (2016).
• N. Bilic, G.B. Tupper, AdS braneworld with backreaction, Cent. Eur. J. Phys.
12 (2014) 147–159.

26. • This work is supported by the SEENET-MTP
Network under the ICTP grant NT-03.
• The financial support of the Serbian Ministry for
Education and Science, Projects OI 174020 and OI
176021 is also kindly acknowledged.

27. T H A N K Y O U!
Х В А Л А !