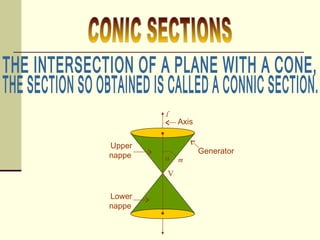
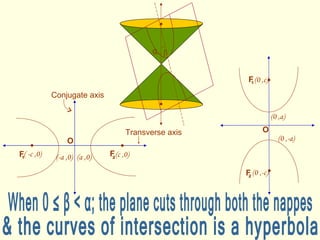
The document discusses different types of conic sections formed by the intersection of a plane with a cone. It defines a conic section as the section obtained from this intersection. It then explains that a circle is formed when the plane is perpendicular to the cone's axis. An ellipse is formed when the plane intersects at an angle between the circle and parabola. A parabola is formed when the plane is tangent to the cone. A hyperbola is formed when the plane intersects both nappes of the cone at different points.

1. PRESENTATION CONIC SECTIONS OF BY:- Sahil Soni

2. CONIC SECTIONS THE INTERSECTION OF A PLANE WITH A CONE, THE SECTION SO OBTAINED IS CALLED A CONNIC SECTION. α V m Lower nappe Upper nappe Axis l Generator

3. SECTIONS OF CONE Plane Cone β α α V m Lower nappe Upper nappe Axis l Generator

4. CIRCLE A CIRCLE IS THE SET OF ALL POINTS IN A PLANE THAT ARE EQUIDISTANT FROM A FIXED POINT IN THE PLANE. O P (x,y) Radius

5. When β = 90°, the section is a circle (h,k) C P (x,y) O (0,0) x² + y ² = r ² (x – h) ² + (y – k) ² α β

6. AN ELLIPSE IS THE SET OF ALL THE POINTS IN A PLANE, THE SUM OF WHOSE DISTANCES FROM TWO FIXED POINTS IN THE PLANE ELLIPSE P P P F F ¹ ³ ² ² ¹

7. When α < β < 90°, the section is an ellipse α β O (0,c) (0,-c) (-b,0) (b,0) (0,-a) (0,a) Y x² y² a ² b ² — — + = 1 x² y² b ² a² — — + = 1 (-c ,0) (c, 0)

8. PARABOLA A Parabola is the set of all points in a plane that are equidistant from a fixed point in the plane. Focus O X' X Y' Y • P (x,y) Directrix

9. When β = α, the section is a parabola α β F (a,0) O x = -a y ² = 4ax X' X Y' Y F (-a,0) O x = +a y ² = -4ax X' X Y ' Y F (0,-a) O y = a x ² = 4ay X' X Y ' Y F (0,a) O y = -a x ² = -4ay X' X Y ' Y

10. A hyperbola is the set of all points in a plane, the difference of whose distances from two fixed points in the plane is a constant. Transverse axis F Conjugate axis F Centre Vertex Vertex HYPERBOLA ² ¹

11. When 0 ≤ β < α; the plane cuts through both the nappes & the curves of intersection is a hyperbola α β Transverse axis F Conjugate axis F (c ,0) (a ,0) ( -c ,0) (-a ,0) O F F (0 ,c) (0 ,a) (0 ,-c) (0 ,-a) O ¹ ¹ ² ²