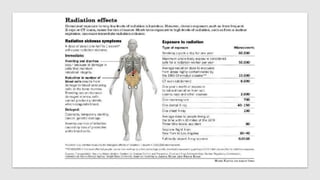
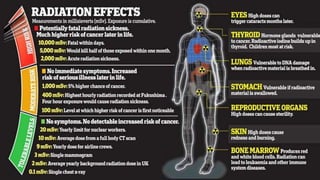
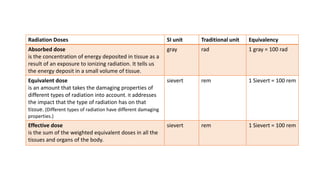
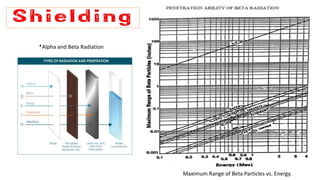
Radiation can cause both acute and chronic effects depending on the exposure level. Acute radiation poisoning occurs with high, short-term exposure and can cause gastrointestinal issues, falling blood counts, and even rapid death. Chronic radiation syndrome occurs after long-term, low-level exposure and may result in blood problems and neurological issues over time. Radiation dose is measured in grays or sieverts, and exposure can be reduced through increasing distance from the source, limiting exposure time, and using appropriate shielding materials like lead or concrete.

1. Radiation: Effects and Dose

2. Radiation effects shows two types of Poisoning
according to the exposure obtained:
Acute Radiation Poisoning
Chronic Radiation Poisoning

3. *Acute radiation syndrome (ARS) also known as radiation poisoning,
radiation sickness or radiation toxicity, is a constellation of health effects
which occur within several months of exposure to high amounts of ionizing
radiation.
Relatively smaller doses
results:
*gastrointestinal effects:
-nausea and vomiting
*symptoms related to falling
blood count:
-infection and bleeding.
Relatively larger
doses can result:
*neurological effects
*rapid death.
Treatment :
*blood transfusions
*antibiotics

4. Chronic radiation syndrome is a constellation of health effects that occur
after months or years of chronic exposure to high amounts of ionizing
radiation.
It may manifest with low
blood cell counts and
neurological problems.
Radiation exposure can also
increase the probability of
developing some other diseases,
mainly different types of cancers.

8. Radiation Doses SI unit Traditional unit Equivalency
Absorbed dose
is the concentration of energy deposited in tissue as a
result of an exposure to ionizing radiation. It tells us
the energy deposit in a small volume of tissue.
gray rad 1 gray = 100 rad
Equivalent dose
is an amount that takes the damaging properties of
different types of radiation into account. It addresses
the impact that the type of radiation has on that
tissue. (Different types of radiation have different damaging
properties.)
sievert rem 1 Sievert = 100 rem
Effective dose
is the sum of the weighted equivalent doses in all the
tissues and organs of the body.
sievert rem 1 Sievert = 100 rem

9. “RADIATION PROTECTION”
*EXTERNAL RADIATION PROTECTION
A.Time
B. Distance
C. Shielding

10. The amount of radiation an individual
accumulates will depend on how long the
individual stays in the radiation field.
Dose (mrem) = Dose Rate (mrem/hr) x Time (hr)
stay time- how long a person can stay in an area
without exceeding a prescribed limit.
Stay Time = DoseRate (mrem/hr) Limit (mrem)
Example:
How long can a radiation worker stay
in a 1.5 rem/hr radiation field if we
wish to limit his dose to 100 mrem?
Stay Time = 1500 mrem/hr 100 mrem
= 0.067 hr
= 4 minutes

11. The amount of radiation an individual receives
will also depend on how close the person is to
the source.
1. The Inverse Square Law
- Point sources of x- and gamma radiation
follow the inverse square law, which states that
the intensity of the radiation (I) decreases in
proportion to the inverse of the distance from the
source (d) squared:
 
 2
1
2
2
2
1
d
d
I
I


12. Example: Radiographer A receives 5 mR per second of scatter
radiation standing 3 feet from the patient. What rate of radiation
does radiographer B standing 7 feet away?
Given
Reqd:
Answer: 0.92 mR/sec
ftd
ftd
mR
I
7
3
sec
5
2
1
1



?2 I

13. Example: The exposure rate one foot from a source is 500 mR/hr.
What would be the exposure rate three feet from the source?
Given:
Reqd:
Answer: 55.56 mR/hr
ftd
ftd
hr
mR
I
3
1
500
2
1
1



?2 I

14. 2. Gamma Exposure Rate Formula
The exposure rate from a gamma point source can be approximated from the following
expression:
Where:
C is the activity of the gamma emitter, in Curies
E is the gamma ray energy in MeV
f is the fraction of disintegrations yielding the gamma of energy E
d is the distance from the source in feet or meter
When d is in feet When d is in meter
I= 6CEf /d2 I= 0.5CEf /d2

15. An individual walks into a room containing a 500-Curie 60Co beam type irradiator. All
indications are that the beam exit port is closed. The individual stands in the path of
the beam and performs work on a piece of medical equipment located approximately
one meter from the source. The individual works for about 5 minutes and then exits
the room. Upon exiting, the individual discovers that the beam port was open the
entire time. You are the resident expert. You are called at home and asked to estimate
the dose received. What is the individual’s estimated dose?
Given:
C= 500 Curie
d= 1 m
t = 5mins
E= 1.33 MeV (see table for Co 60)
f = 0.9998 (see table for Co 60)
Required:
Dose=?
Answer: 28 R

16. When reducing the time or increasing the distance may not be possible,
one can choose shielding material to reduce the external radiation hazard.
The proper material to use depends on the type of radiation and its
energy.
*Alpha and Beta Radiation
*X and Gamma Radiation
*Half Value Layer

17. *Alpha and Beta Radiation
Maximum Range of Beta Particles vs. Energy.

18. *X and Gamma Radiation
Monoenergetic x- or gamma rays collimated into a narrow beam are
attenuated exponentially through a shield according to the following
equation:
I = Ioe-μx
Where:
I is the intensity outside of a shield of thickness x
Io is the unshielded intensity
μ is the linear attenuation coefficient of the shielding material
x is the thickness of shielding material.

19. *X and Gamma Radiation
The linear attenuation coefficient, μ, is the sum of the probabilities of
interaction per unit path length by each of the three scattering and
absorption processes - photoelectric effect, Compton effect, and pair
production. Note that μ has dimensions of inverse length (1/cm).
Mass attenuation coefficient : μm =
μ
𝜌
Where
μm = cm2/g
𝜌 = density (g/cm3)

20. Example: What is the dose rate after shielding a source that emits only 1 MeV
photons if the unshielded dose rate is 100 mrem/h and the source is shielded
by 1/2 inch lead?
Given:
Io = 100 mrem/hr
X= 0.5 in Pb
From the table @ 1 MeV:
𝜌 = 11.35 g/cm3
μm=0.068 cm2/g
Required:
I = ?
Answer: 37mrem/hr

21. *Half Value Layer
The half value layer (HVL) is the thickness of a shielding material required
to reduce the intensity of radiation at a point to one half of its original
intensity. It can be calculated by setting I=0.5Io and solving the
attenuation equation for x:
From the equation:
I = Ioe-μx
Let I=0.5Io Thus,
0.5Io= Ioe-μx
0.5=e-μx
HVLX 

5.0ln
5.0

22. Determine the lead HVL for Cs-137 photons (0.662 MeV) using the shielding
equation.
Given:
E=0.662 MeV
From the Table:
μm=0.107 cm2/g
𝜌 = 11.35 g/cm3
Required:
HVL=?
Answer: 0.57 cm Pb