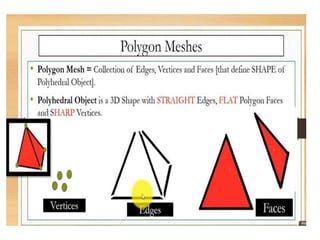
This document discusses different representations of surfaces in 3D modeling, including polygon meshes, parametric surfaces, and quadric surfaces. Polygon meshes represent surfaces as sets of connected planar polygons, and are suitable for boxes and buildings but not curved surfaces. Parametric surfaces represent points on 3D curves or surfaces as polynomial functions of parameters, allowing more accurate curved representations using fewer data points than polygon meshes. Higher-order parametric curves are more compact and easier to manipulate than polylines.

1. 1
Polygon Mesh

2. 2
• We need smooth curves and surfaces in
many applications:
– model real world objects
– computer-aided design (CAD)
– high quality fonts
– data plots
– artists sketches

3. 3
Introduction
• Most common representation for surfaces:
– polygon mesh
– parametric surfaces
– quadric surfaces
• Solid modeling
– don’t miss the next episode...

4. 4
Introduction
• Polygon mesh:
– set of connected planar surfaces bounded by
polygons
– good for boxes, cabinets, building exteriors
– bad for curved surfaces
– errors can be made arbitrarily small at the cost
of space and execution time
– enlarged images show geometric aliasing

5. 5
Introduction
• Parametric polynomial curves:
– point on 3D curve = (x(t), y(t), z(t))
– x(t), y(t), and z(t) are polynomials
– usually cubic: cubic curves

6. 6
Introduction
• Parametric bivariate (two-variable)
polynomial surface patches:
– point on 3D surface = (x(u,v), y(u,v), z(u,v))
– boundaries of the patches are parametric
polynomial curves
– many fewer parametric patches than
polynomial patches are needed to approximate
a curved surface to a given accuracy
– more complex algorithms though

7. 7
Parametric cubic curves
• Polylines and polygons:
– large amounts of data to achieve good accuracy
– interactive manipulation of the data is tedious
• Higher-order curves:
– more compact (use less storage)
– easier to manipulate interactively
• Possible representations of curves:
– explicit, implicit, and parametric

8. 8
Parametric cubic curves
• Polylines and polygons:
– large amounts of data to achieve good accuracy
– interactive manipulation of the data is tedious
• Higher-order curves:
– more compact (use less storage)
– easier to manipulate interactively
• Possible representations of curves:
– explicit, implicit, and parametric