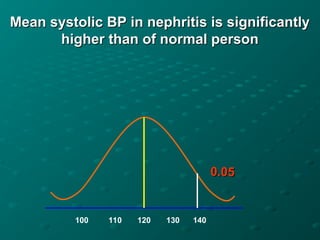
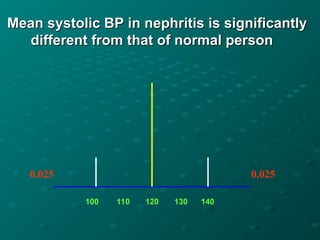
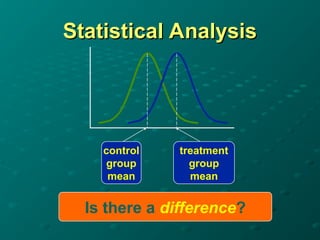
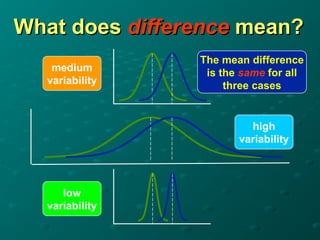
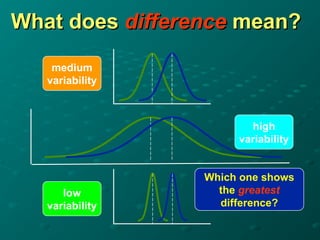
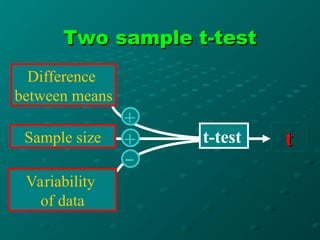
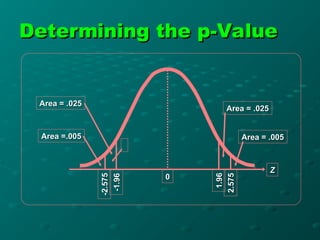
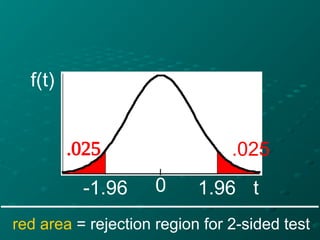
The document discusses the t-distribution and the t-test, which was invented by William Gosset, also known as 'Student', for analyzing small sample sizes particularly in quality control. It outlines different types of t-tests, including one-sample, unpaired, and paired tests, along with hypotheses setup and statistical analysis considerations like p-values and assumptions for validity. The conclusion emphasizes the appropriate scenarios for using the t-test, particularly when sample sizes are small and for comparing means.

1. The t-distribution
The t-distribution
William Gosset
lived from 1876 to 1937
Gosset invented the t -test to handle small samples for quality
control in brewing. He wrote under the name "Student".

2. t test-origin
t test-origin
Founder WS Gosset
Founder WS Gosset
Wrote under the pseudonym “Student”
Wrote under the pseudonym “Student”
Mostly worked in tea (t) time
Mostly worked in tea (t) time
? Hence known as Student's
? Hence known as Student's t
t test.
test.
Preferable when the n < 60
Preferable when the n < 60
Certainly if n
Certainly if n <
< 30
30

3. Types
Types
One sample
One sample
compare with population
compare with population
Unpaired
Unpaired
compare with control
compare with control
Paired
Paired
same subjects: pre-post
same subjects: pre-post

4. T-test
T-test
1.
1. Test for single mean
Test for single mean
Whether the sample mean is equal to the predefined
population mean ?
2. Test for difference in means
. Test for difference in means
Whether the CD4 level of patients taking treatment A is
equal to CD4 level of patients taking treatment B ?
3. Test for paired observation
Test for paired observation
Whether the treatment conferred any significant benefit ?

5. Test direction
Test direction
One tailed t test
One tailed t test
Two tailed test
Two tailed test

6. Developing the
Pooled-Variance t Test (Part 1)
•Setting Up the Hypothesis:
H0: 1 -2 = 0
H1: 1 - 2
 0
H0: 1 = 2
H1: 1  2
OR
Two
Tail

7. Mean systolic BP in nephritis is significantly
Mean systolic BP in nephritis is significantly
higher than of normal person
higher than of normal person
100 110 120 130 140
0.05
0.05

8. Mean systolic BP in nephritis is significantly
Mean systolic BP in nephritis is significantly
different from that of normal person
different from that of normal person
0.025 0.025
100 110 120 130 140

9. Statistical Analysis
Statistical Analysis
control
group
mean
treatment
group
mean
Is there a difference?

10. What does
What does difference
difference mean?
mean?
medium
variability
high
variability
low
variability
The mean difference
is the same for all
three cases

11. What does
What does difference
difference mean?
mean?
medium
variability
high
variability
low
variability
Which one shows
the greatest
difference?

12. What does
What does difference
difference mean?
mean?
a statistical difference is a function of the
a statistical difference is a function of the
difference between means
difference between means relative to the
relative to the
variability
variability
a small difference between means with
a small difference between means with
large variability could be due to
large variability could be due to chance
chance
like a
like a signal-to-noise
signal-to-noise ratio
ratio
low
variability
Which one shows
the greatest
difference?

13. So we estimate
So we estimate
low
variability
signal
noise
difference between group means
variability of groups
=
XT - XC
SE(XT - XC)
=
= t-value
_ _
_ _

14. Two sample t-test
Two sample t-test
Difference
between means
Sample size
Variability
of data
t-test t
t
+
+

15. Probability - p
Probability - p
With t we check the probability
With t we check the probability
Reject or do not reject Null hypothesis
Reject or do not reject Null hypothesis
You reject if p < 0.05 or still less
You reject if p < 0.05 or still less
Difference between means (groups) is
Difference between means (groups) is
more & more significant if p is less & less
more & more significant if p is less & less

16. -1.96
-1.96
0
0
Area = .025
Area = .025
Area =.005
Area =.005
Z
Z
-2.575
-2.575 Area = .025
Area = .025
Area = .005
Area = .005
1.96
1.96
2.575
2.575
Determining the p-Value
Determining the p-Value

17. .95
t
0
f(t)
-1.96 1.96
.025

red area = rejection region for 2-sided test

18. Assumptions
Assumptions
Normal distribution
Normal distribution
Equal variance
Equal variance
Random sampling
Random sampling

19. t-Statistic
t-Statistic
n
s
x
t
/



When the sampled population is normally
When the sampled population is normally
distributed, the t statistic is Student t
distributed, the t statistic is Student t
distributed with n-1 degrees of freedom.
distributed with n-1 degrees of freedom.

20. T- test for single mean
T- test for single mean
The following are the weight (mg) of each of 20
rats drawn at random from a large stock. Is it
likely that the mean weight of these 20 rats are
similar to the mean weight ( 24 mg) of the whole
stock ?
9 18 21 26
14 18 22 27
15 19 22 29
15 19 24 30
16 20 24 32

21. Steps for test for single mean
Steps for test for single mean
1. Questioned to be answered
Is the Mean weight of the sample of 20 rats is 24 mg?
N=20, =21.0 mg, sd=5.91 , =24.0 mg
2. Null Hypothesis
The mean weight of rats is 24 mg. That is, The
sample mean is equal to population mean.
3. Test statistics --- t (n-1) df
4. Comparison with theoretical value
if tab t (n-1) < cal t (n-1) reject Ho,
if tab t > cal t accept Ho,
n
s
x
t
/



x 

22. t –test for single mean
t –test for single mean
Test statistics
Test statistics
n=20, =21.0 mg, sd=5.91 ,
n=20, =21.0 mg, sd=5.91 ,
=24.0 mg
=24.0 mg
t
t
 = t
= t .05, 19
.05, 19 = 2.093
= 2.093 Accept H
Accept H0
0 if t < 2.093
if t < 2.093 Reject
Reject
H
H0
0 if t >= 2.093
if t >= 2.093
x
30
.
2
20
91
.
5
24
0
.
21




l
l
t

Inference :
Inference :
There is no evidence that the sample is taken
There is no evidence that the sample is taken
from the population with mean weight of 24 gm
from the population with mean weight of 24 gm

23. In Conclusion !
In Conclusion !
Student ‘s t-test will be used:
Student ‘s t-test will be used:
--- When Sample size is small
--- When Sample size is small
and for the following situations:
and for the following situations:
(1) to compare the single sample mean
(1) to compare the single sample mean
with the population mean
with the population mean
(2) to compare the sample means of
(2) to compare the sample means of
two indpendent samples
two indpendent samples
(3) to compare the sample means of
(3) to compare the sample means of
paired samples
paired samples