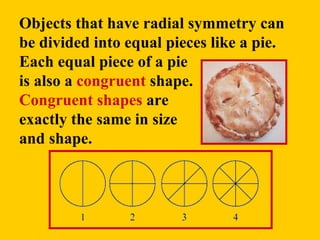
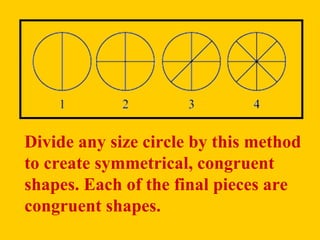
Radial symmetry is a type of balance where parts of an object are arranged around a central point. There are three types of balance: radial symmetry, mirror/bilateral symmetry, and asymmetry. Radial symmetry is seen in both natural objects like snowflakes and human-made objects like mandalas, kaleidoscopes, and rose windows in cathedrals. To create radial symmetry, a circle is divided into equal sections and the same pattern is repeated in each section.