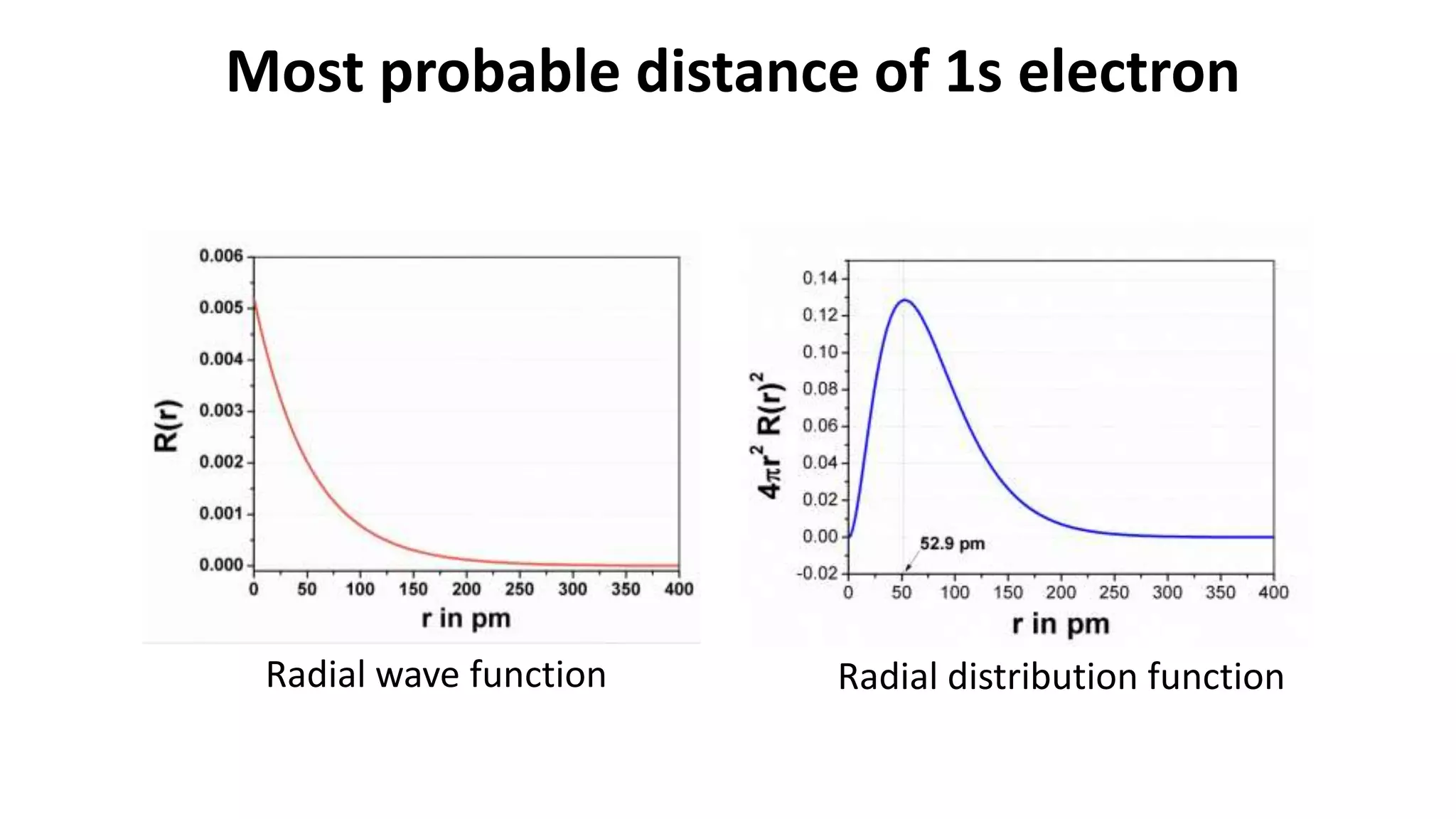
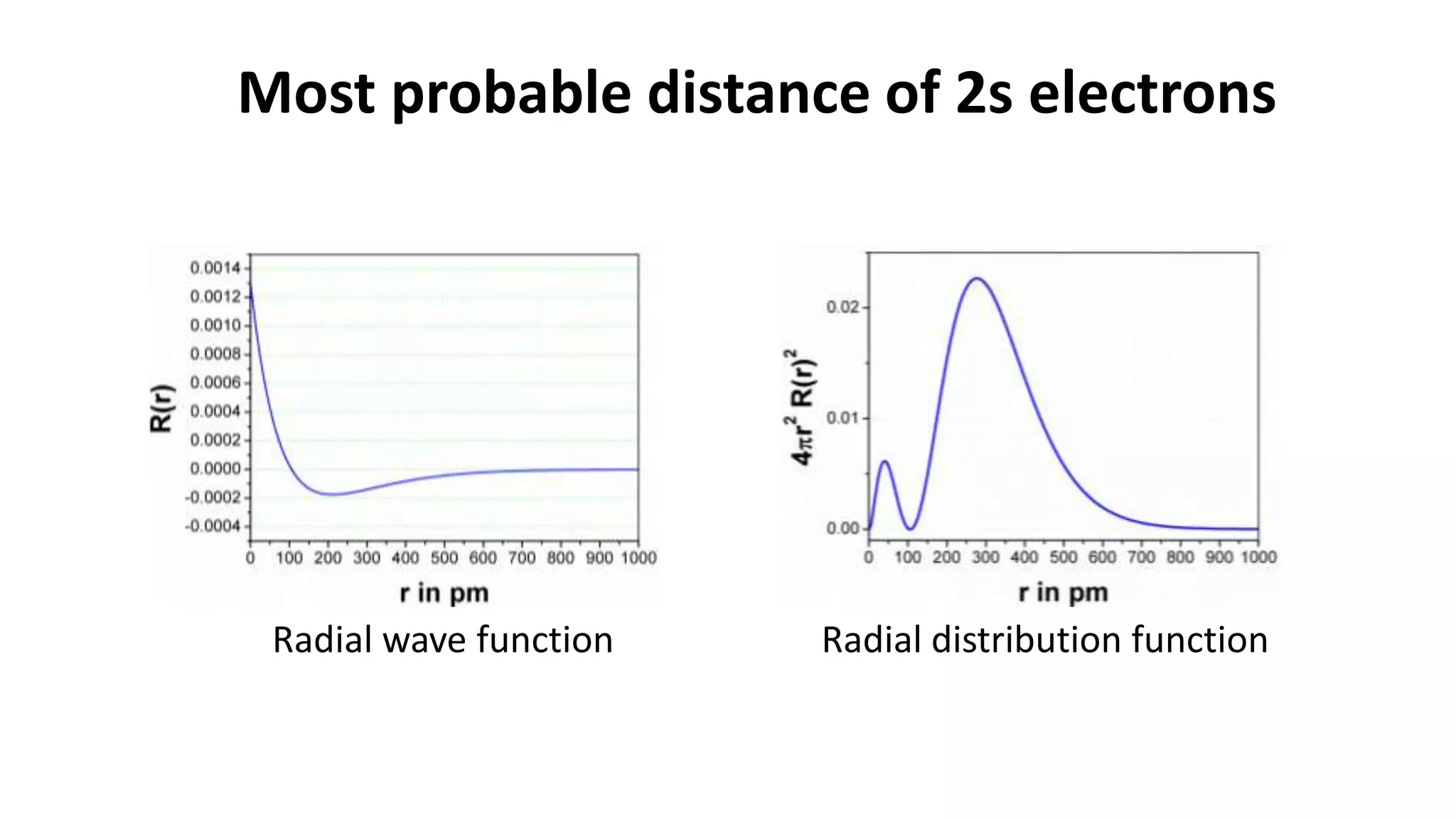
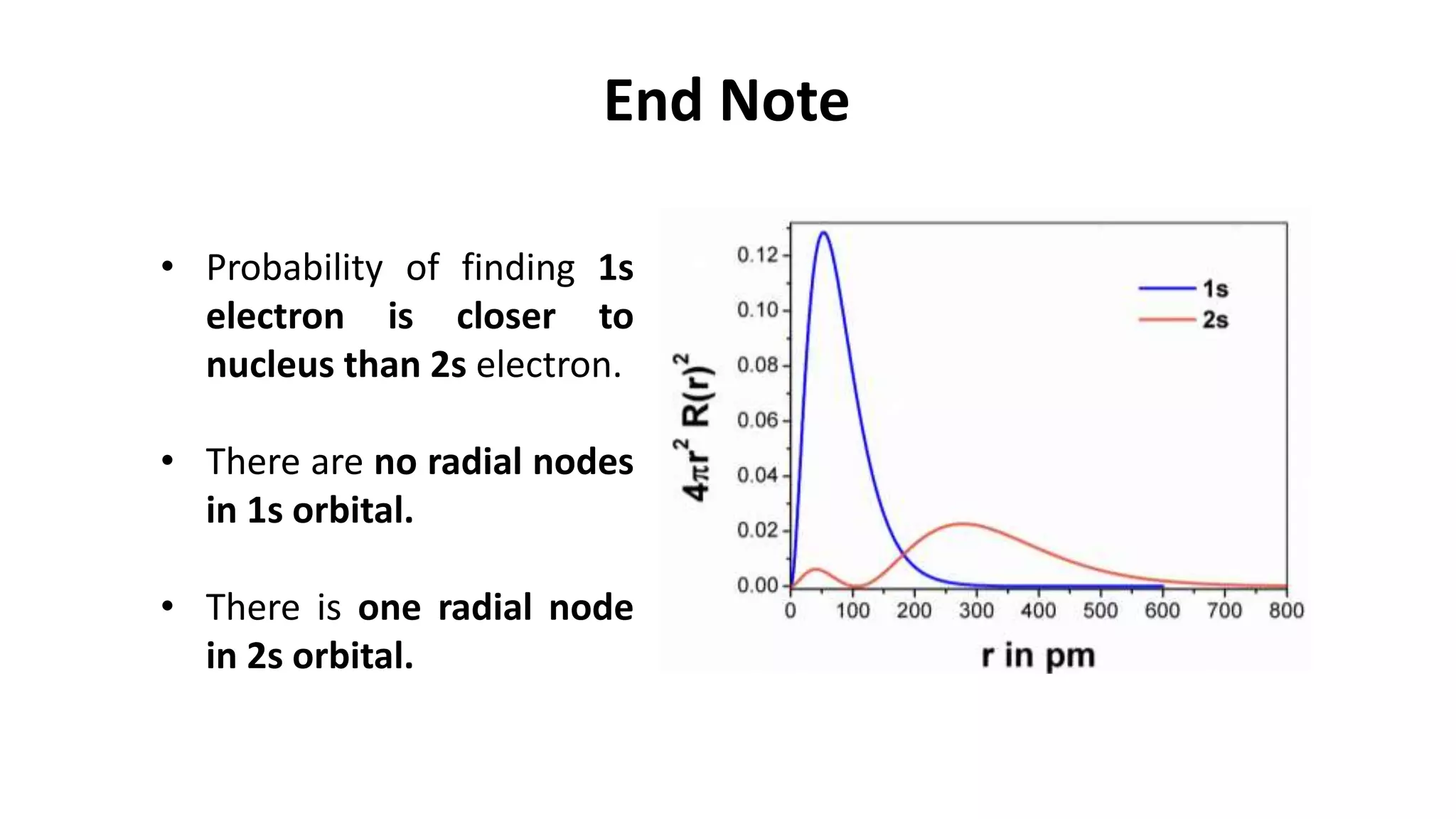
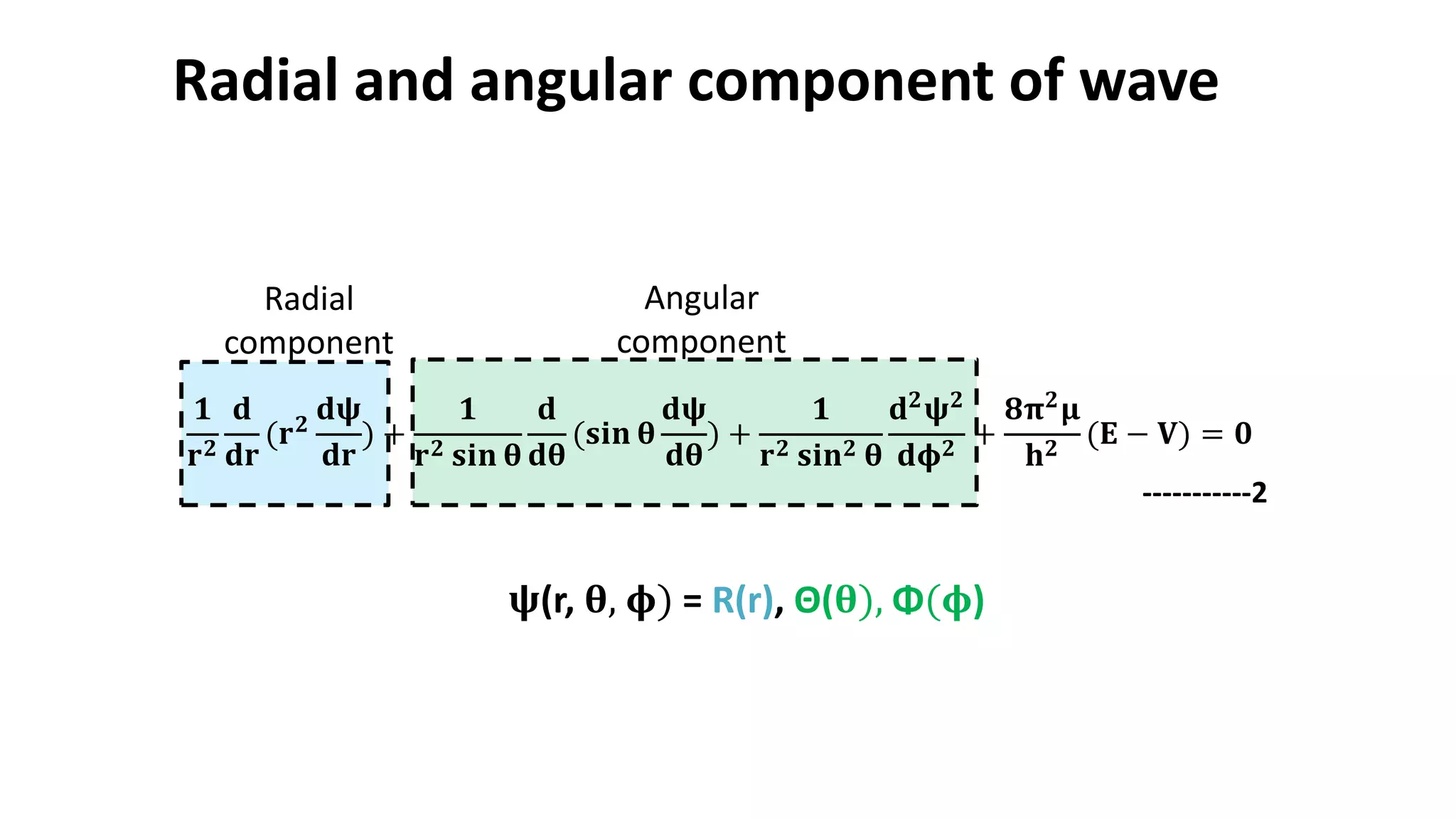
The document discusses the radial and angular parts of the hydrogenic wave functions. It shows how the Schrodinger equation can be written using both Cartesian and polar coordinates. The radial component R(r) of the wave function gives the distribution of electrons as a function of radius r from the nucleus. R(r) depends on the principal quantum number n and azimuthal quantum number l. Graphs and equations are provided to show the radial wave functions and most probable distances for 1s and 2s orbitals.

1. Radial and angular parts of the
hydrogenic wave functions

2. 𝐝𝟐𝛙
𝐝𝐱𝟐
+
𝐝𝟐𝛙
𝐝𝐲𝟐
+
𝐝𝟐𝛙
𝐝𝐳𝟐
+
𝟖𝛑𝟐𝐦
𝐡𝟐
(𝐄 − 𝐕) = 𝟎
-----------1
Schrodinger equation with Cartesian coordinates

3. Cartesian coordinates and polar
coordinates
θ
φ r
(x, y, z) or (r, θ, φ)
x axis
z
axis
x = r sin θ cos ϕ
y = r sin θ sin ϕ
z = r cos θ
m = μ

4. 𝟏
𝐫𝟐
𝐝
𝐝𝐫
(𝐫𝟐
𝐝𝛙
𝐝𝐫
) +
𝟏
𝐫𝟐 𝐬𝐢𝐧 𝛉
𝐝
𝐝𝛉
(𝐬𝐢𝐧 𝛉
𝐝𝛙
𝐝𝛉
) +
𝟏
𝐫𝟐 𝐬𝐢𝐧𝟐 𝛉
𝐝𝟐
𝛙𝟐
𝐝𝛟𝟐
+
𝟖𝛑𝟐
𝛍
𝐡𝟐
(𝐄 − 𝐕) = 𝟎
-----------2
Schrodinger equation with polar
coordinates
We have,

5. 𝟏
𝐫𝟐
𝐝
𝐝𝐫
(𝐫𝟐
𝐝𝛙
𝐝𝐫
) +
𝟏
𝐫𝟐 𝐬𝐢𝐧 𝛉
𝐝
𝐝𝛉
(𝐬𝐢𝐧 𝛉
𝐝𝛙
𝐝𝛉
) +
𝟏
𝐫𝟐 𝐬𝐢𝐧𝟐 𝛉
𝐝𝟐
𝛙𝟐
𝐝𝛟𝟐
+
𝟖𝛑𝟐
𝛍
𝐡𝟐
(𝐄 − 𝐕) = 𝟎
-----------2
𝛙(r, 𝛉, 𝛟) = R(r), Θ(𝛉), Φ(𝛟)
Radial and angular component of wave
Angular
component
Radial
component

6. Radial component ‘R(r)’ of wave function ′𝛙’ gives the distribution
of electron as a function of radius ‘r’(distance from the nucleus)
Radial wave function = R(r)
Radial component of wave function

7. Radial wave function depends on principle quantum number ‘𝒏’
and azimuthal quantum number ‘l’ and have a common function
𝐞−𝒁𝒓/𝒏𝒂°
Where,
r = distance from nucleus
e = base of natural logarithm
Z = atomic number
𝑎°= Bohr radius (52.9 pm)
𝑛 = principal quantum number
Distribution curves for the Radial wave function

8. Orbital
Quantum
number
Radial component of wave function
‘R(r)’
1s n = 1, l = 0 2(
𝑧
𝑎°
)3/2
𝑒−𝑍𝑟/𝑛𝑎°
2s n = 2, l = 0
1
8
1
2
𝑧
𝑎°
3
2
2 −
2𝑍r
n𝑎°
𝑒−𝑍𝑟/𝑛𝑎°
‘[R(r)]2’ gives the probability of finding electron.
Distribution curves for the Radial wave function

9. r in pm R(r) [R(r)]2 4πr2 [R(r)]2
0 0.005198122 2.70205E-05 0
52.5 0.001926797 3.71255E-06 0.128522758
52.9 0.001912282 3.65682E-06 0.128530144
53.5 0.001890715 3.5748E-06 0.128513735
224.8 7.41823E-05 5.50301E-09 0.003492872
R(r) =2(
𝑧
𝑎°
)3/2
𝑒−𝑍𝑟/𝑛𝑎°
Most probable distance of 1s electron

10. Radial wave function Radial distribution function
Most probable distance of 1s electron

11. R(r) =
𝟏
𝟖
𝟏
𝟐
𝒛
𝒂°
𝟑
𝟐
𝟐 −
𝟐𝒁𝒓
𝒏𝒂°
𝒆−𝐙𝐫/𝐧𝒂°
Most probable distance of 2s electrons

12. Radial distribution function
Radial wave function
Most probable distance of 2s electrons

13. • Probability of finding 1s
electron is closer to
nucleus than 2s electron.
• There are no radial nodes
in 1s orbital.
• There is one radial node
in 2s orbital.
End Note

14. You can read more always
• Lee, J. D., (2018), Concise Inorganic Chemistry, Fifth Edition, New
Delhi, Wiley India.
• Huheey, J. E., Keiter, E. A., Keiter, R. L., Medhi, O. K., (2019) Inorganic
Chemistry: Principle of structure and reactivity, Fourth Edition, Noida,
Pearson Education India.
• Atkins, P., Overton T., Rourke, J., Weller, M., Armstrong F., (2006)
Shriver and Atkin’s Inorganic Chemistry, Fourth Edition, Great Britain,
Oxford University Press.