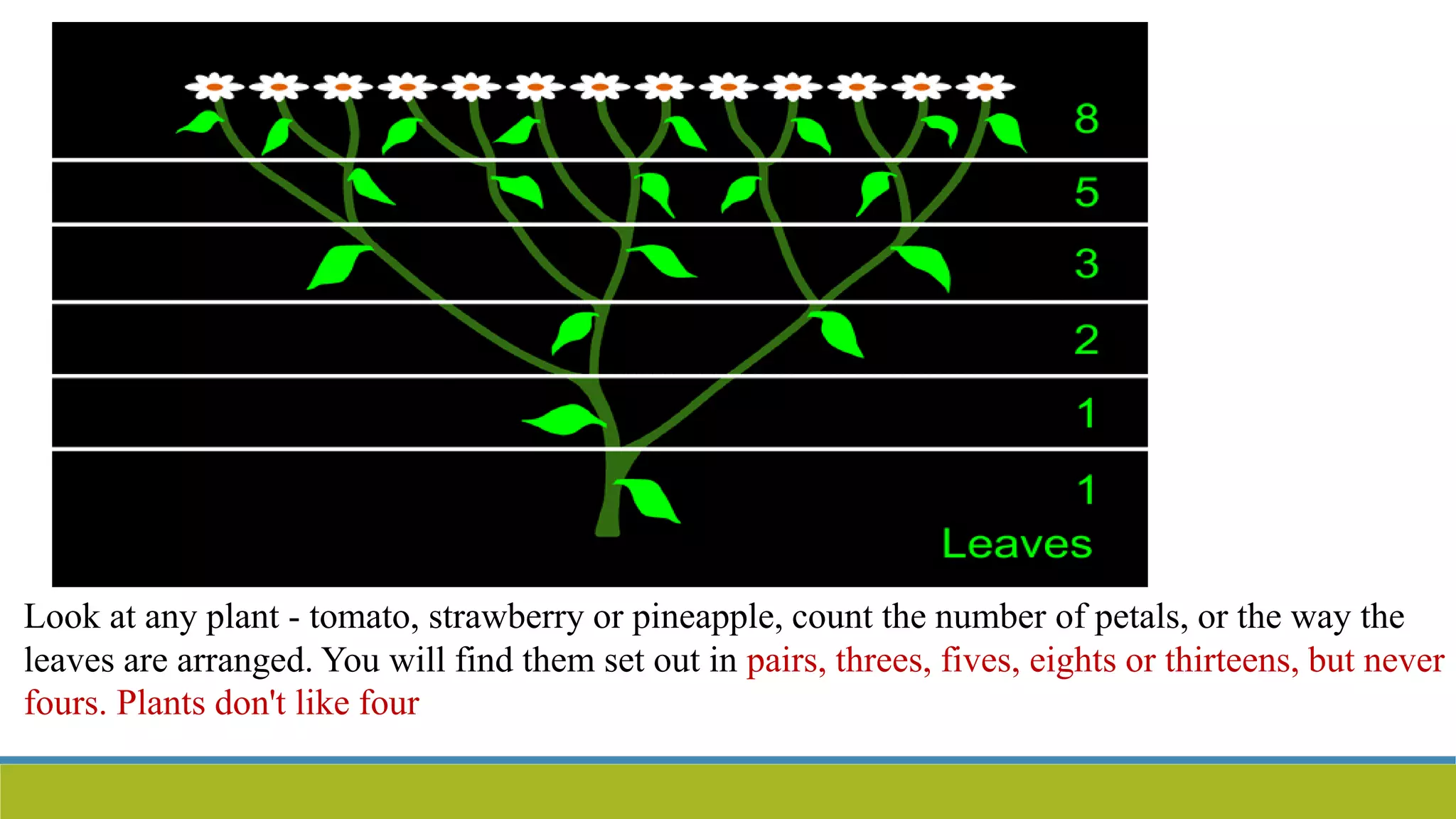
The document discusses the Fibonacci sequence, which is a series of numbers where each subsequent number is the sum of the previous two. This sequence appears frequently in nature, such as the arrangement of petals and leaves in plants. The document provides the formula to calculate any term in the Fibonacci sequence and works through examples of computing specific terms like F17 and F20. It also gives very large values for later terms like F153 and F260.

3. 1, 1, 2, 3, 5, 8, 13, 21, 34

4. Look at any plant - tomato, strawberry or pineapple, count the number of petals, or the way the
leaves are arranged. You will find them set out in pairs, threes, fives, eights or thirteens, but never
fours. Plants don't like four

5. Fibonacci Sequence
The Fibonacci Sequence is the series of numbers:
F1 F2 F3 F4 F5 F6 F7 F8 F9 F10 F 11 F 12 F 13 F 14….F15
1, 1, 2, 3, 5, 8, 13, 21, 34, 55 89 144 233 377 610
The next number is found by adding up the two numbers before it.
 The 2 is found by adding the two numbers before it (1+1)
 The 3 is found by adding the two numbers before it (1+2),
 And the 5 is (2+3),

6. Example: the 8th term is
the 7th term plus the 6th term:
x8 = x7 + x6
F1 F2 F3 F4 F5 F6 F7 F8 F9 F10 F 11 F 12 F 13 F 14….F15
1, 1, 2, 3, 5, 8, 13, 21, 34, 55 89 144 233 377 610

7. The Fibonacci Sequence is the series of numbers:
F1 F2 F3 F4 F5 F6 F7 F8 F9 F10 F 11 F 12 F 13 F 14 F 15
1, 1, 2, 3, 5, 8, 13, 21, 34, 55 89 144 233 377 610
Compute for
F 16 =
F17 =
F 18 =
F 100 =

8. Binet's Formula
Binet's formula is an explicit formula used to find the nth term
of the Fibonacci sequence.
It is so named because it was derived by mathematician
Jacques Philippe Marie Binet

9. F n = 1 + √ 5 n
2
√ 5
Using scientific calculator
Press the following keys 1 + √ 5 = / 2 = ^ 17 = / √ 5 =
• Use the appropriate key for division
• F 17 = ?
• F 17 = 1596.99 or 1597
• F 20 = ?
• F 20 = 6765 1 + √ 5 = / 2 = ^ 20 / √ 5 =

10. 1.345678 x 10 ^ 10
1.3457 x 10 ^ 10
2.3942468 E – 8
2.3942 x 10 ^ 8
F153 = 4.2230 x 10 ^ 31
F 260 = 9.7118 x 10 ^ 53
F162 = 3.2101 x 10 ^ 33
F33 = 3,524,578
F 79 = 1.4472 x 10 ^ 16
F 143 = 3.4336 x 10 ^ 29