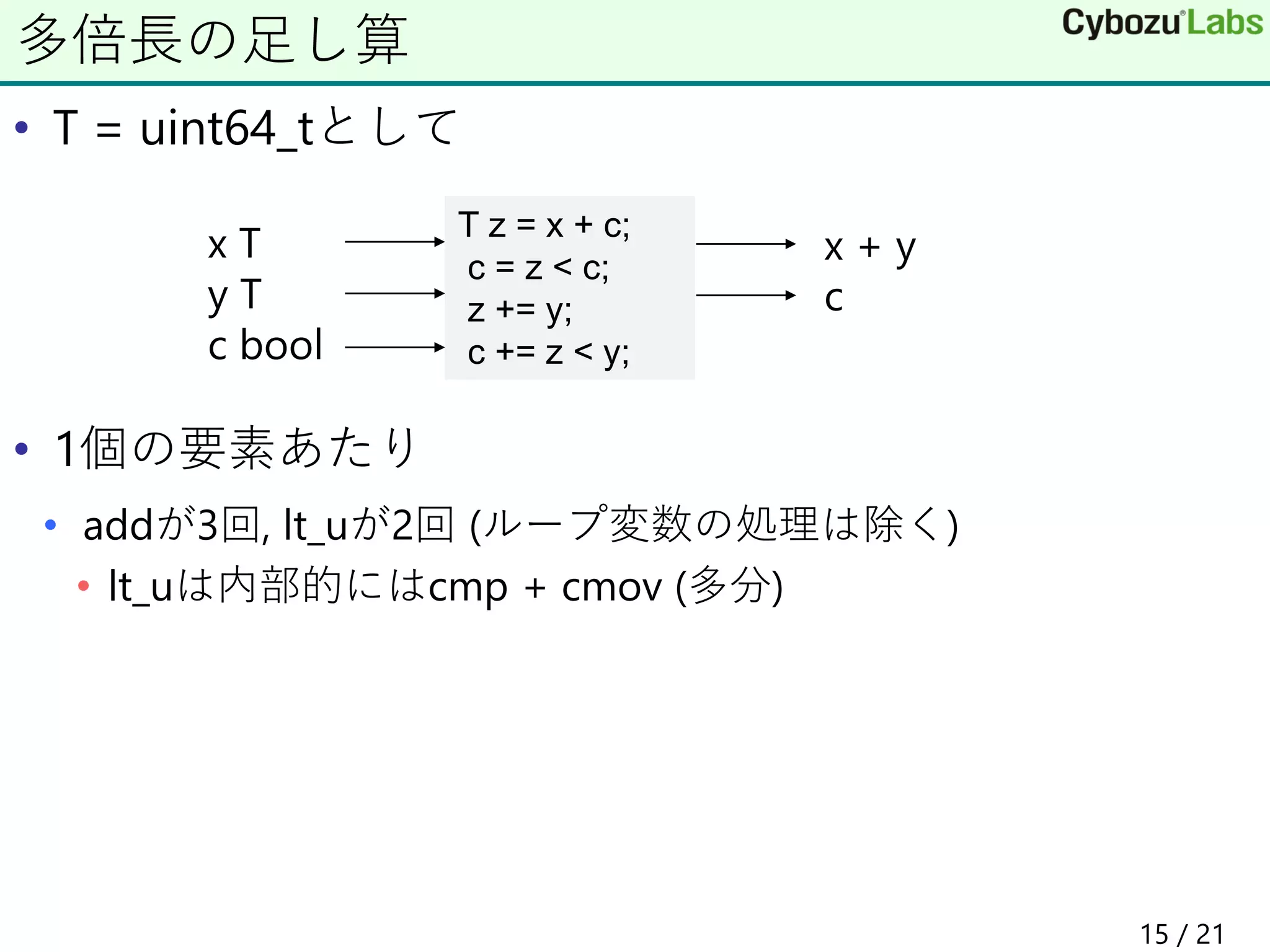
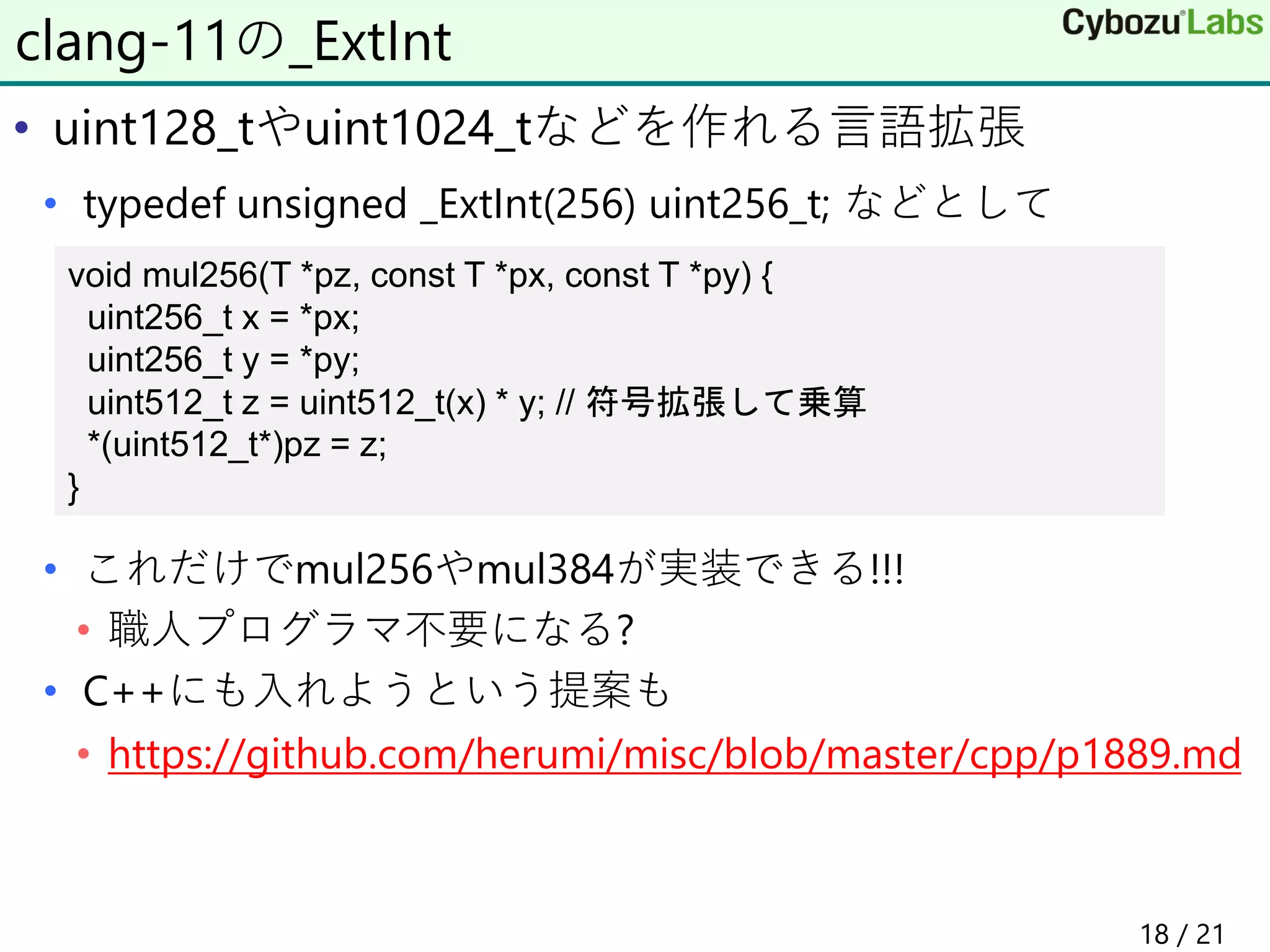
The document discusses implementing multiple-precision arithmetic in WebAssembly. It describes how carry operations are important for multiple-precision addition and multiplication but are not supported natively in WebAssembly. It proposes some strategies for emulating carry operations in WebAssembly using instructions like add, lt_u, and select to add multiples of 64-bit elements with carry propagation. Benchmark results show that 32-bit element processing can outperform 64-bit element processing for some operations like multiplication in WebAssembly. Overall, implementing efficient multiple-precision arithmetic in WebAssembly requires emulating carry operations that are supported directly in x64 processors.




![• ペアリングには楕円曲線が必要だ
• 楕円曲線には拡大体や有限体が必要だ
• 有限体には固定多倍長演算が必要だ
• 𝑥, 𝑦, 𝑝を384bit (or 256bit)整数として
• 𝑥 ± 𝑦 % 𝑝, 𝑥 ∗ 𝑦 % 𝑝 の計算を多数行う
• 足し算や掛け算ってどうやってするの? ← 今日の本題
• しばらくx86-64で解説
• 後半wasmでの方針を解説
• その前に記号
• 𝑥 = [𝑥3: 𝑥2: 𝑥1: 𝑥0]と書くと𝑥0, … , 𝑥3は符号無し64bit整数で
𝑥 = 𝑥3 ∗ 2192 + 𝑥2 ∗ 2128 + 𝑥1 ∗ 264 + 𝑥0を表すことにする
ブレイクダウン
7 / 21](https://image.slidesharecdn.com/kernelvm-20210320-210320074736/75/WebAssembly-7-2048.jpg)
![• 64bitのレジスタ𝑎, 𝑏の和は65bit
• Intel CPUでadd 𝑎, 𝑏は𝑎 += 𝑏;の意味
• 残り1bitはCarryフラグ (CF)で表す ; [CF:a] = a+b
• [𝑦1: 𝑦0] + [𝑥1: 𝑥0]は
• add 𝑦0, 𝑥0 ; 𝑦0 += 𝑥0, CF= 0 or 1
• adc 𝑦1, 𝑥1 ; 𝑦1 += 𝑥1 +CF ; carryつきのadd
• AArch64ではaddsとadcs
2桁の足し算36 + 47 = ?
3 6
+ 4 7
-----
1 3
3
4
-----
8 3
繰り上がり
8 / 21](https://image.slidesharecdn.com/kernelvm-20210320-210320074736/75/WebAssembly-8-2048.jpg)
![• 𝑦3: 𝑦2: 𝑦1: 𝑦0 += [𝑥3: 𝑥2: 𝑥1: 𝑥0]
• では73 * 7 = ?
• x64のmul命令は64x64→128
mul x ; [rdx:rax] ← x * rax
AArch64は上位・下位64bit取得のmul
mulとumulh
mulしてからcarryつきadd
4桁の足し算
add 𝑦0, 𝑥0
adc 𝑦1, 𝑥1
adc 𝑦2, 𝑥2
adc 𝑦3, 𝑥3
7 3 𝑦1 𝑦0
* 7 𝑥0
----- -------
2 1 |𝑦0 𝑥0|
4 9 |𝑦1 𝑥0|
----- ---------
5 1 1
繰り上がり
9 / 21](https://image.slidesharecdn.com/kernelvm-20210320-210320074736/75/WebAssembly-9-2048.jpg)

![• CFを破壊しない
• mov rdx, x / mulx H, L, y ; [H:L] = x * y
mulx登場 (from Haswell)
mov rdx, x ; rdx ← x
mulx z1, z0, y0
mulx z2, t, y1
add z1, t
mulx z3, t, y2
adc z2, t
mulx z4, t, y3
adc z3, t
adc z4, 0
[y3:y2:y1:y0]
* x
----------------------
[z1:z0]
[z2: t]
[z3: t]
[z4: t]
-----------------------
[z4:z3:z2:z1:z0]
11 / 21](https://image.slidesharecdn.com/kernelvm-20210320-210320074736/75/WebAssembly-11-2048.jpg)
![• 途中に「𝑦𝑥𝑖−1 += 𝑦𝑥𝑖」
• 問題発生!
• 𝑦𝑥𝑖を計算するときにCFを使う
• 𝑦𝑥1の計算が終わらないと𝑦𝑥0に𝑦𝑥1を足せない
• レジスタ圧迫
[𝑦3: 𝑦2: 𝑦1: 𝑦0]*[𝑥3: 𝑥2: 𝑥1: 𝑥0]
[y3:y2:y1:y0]
x [x3:x2:x1:x0]
---------------------------------
[ y x0 ]
[ y x 1 ]
[ y x2 ]
[ y x3 ]
-----------------------------------
[z7:z6:z5:z4:z3:z2:z1:z0]
12 / 21](https://image.slidesharecdn.com/kernelvm-20210320-210320074736/75/WebAssembly-12-2048.jpg)
![• 問題点はCFが1個しかないこと
• 2個あれば𝑦𝑥1を計算しながら𝑦𝑥0に足せる
• adcx ; CFつきの加算
• adox ; OFつきの加算
• CFとOFを独立した1bitレジスタとして扱う
• [z] += [y] * x
• [y] * xの計算にCFを使う
• [z] += の計算にOFを使う
• 中間レジスタ数低減
• BroadwellやRyzenで対応
adcx, adox登場
[ z ]
[y0 x1]
[y1 x1]
[y2 x1]
[y3 x1]
-----------------------------------
[z5:z4:z3:z2:z1:z0]
adcx
adox
13 / 21](https://image.slidesharecdn.com/kernelvm-20210320-210320074736/75/WebAssembly-13-2048.jpg)