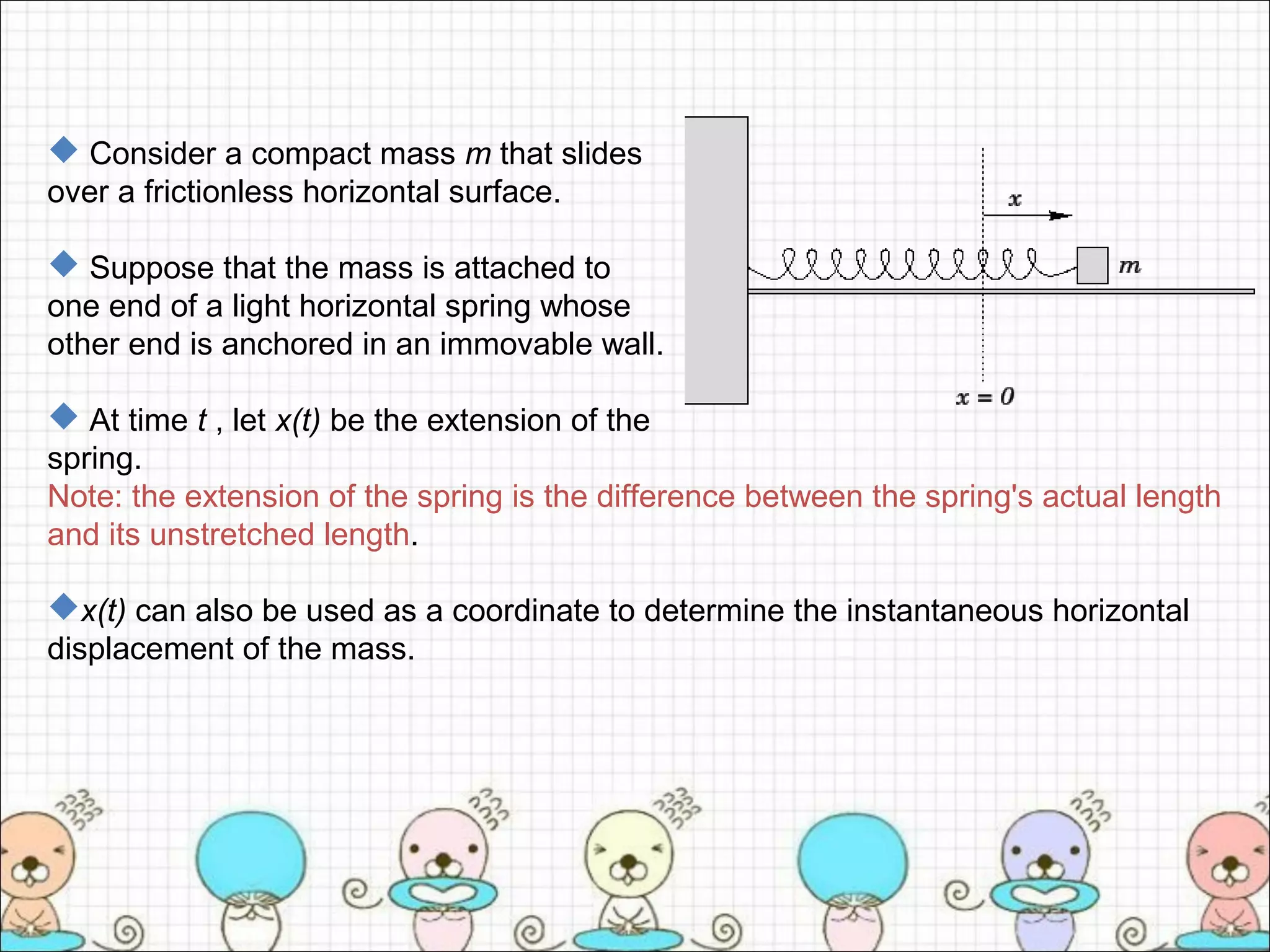
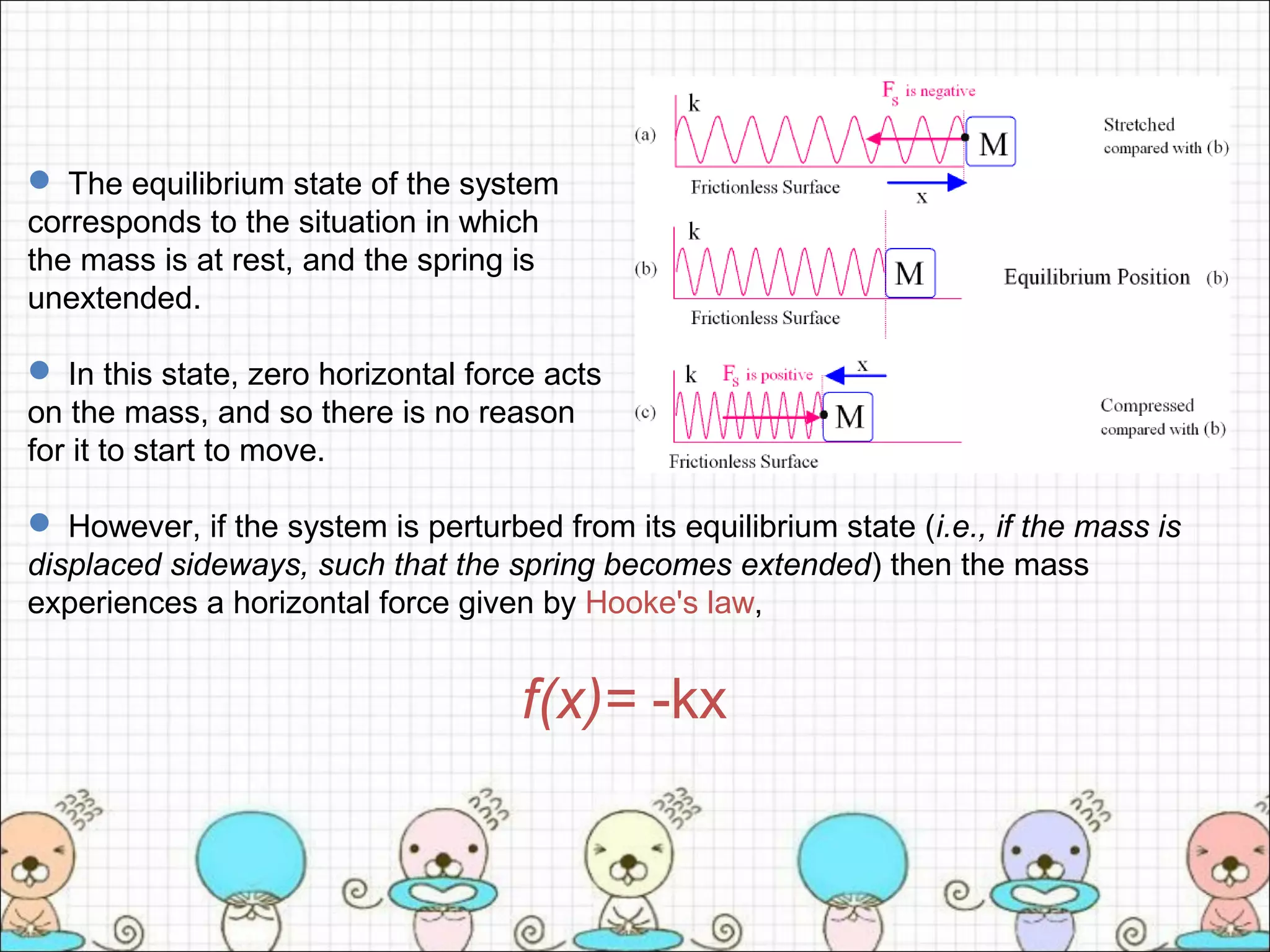
- A mass m is attached to one end of a horizontal spring, while the other end is anchored to a wall. The extension x(t) of the spring from its unstretched length determines the horizontal displacement of the mass. - When undisturbed, the mass is at rest and the spring is unextended. But if displaced from this equilibrium, the spring exerts a restoring force f(x) = -kx on the mass according to Hooke's law, where k is the spring constant. 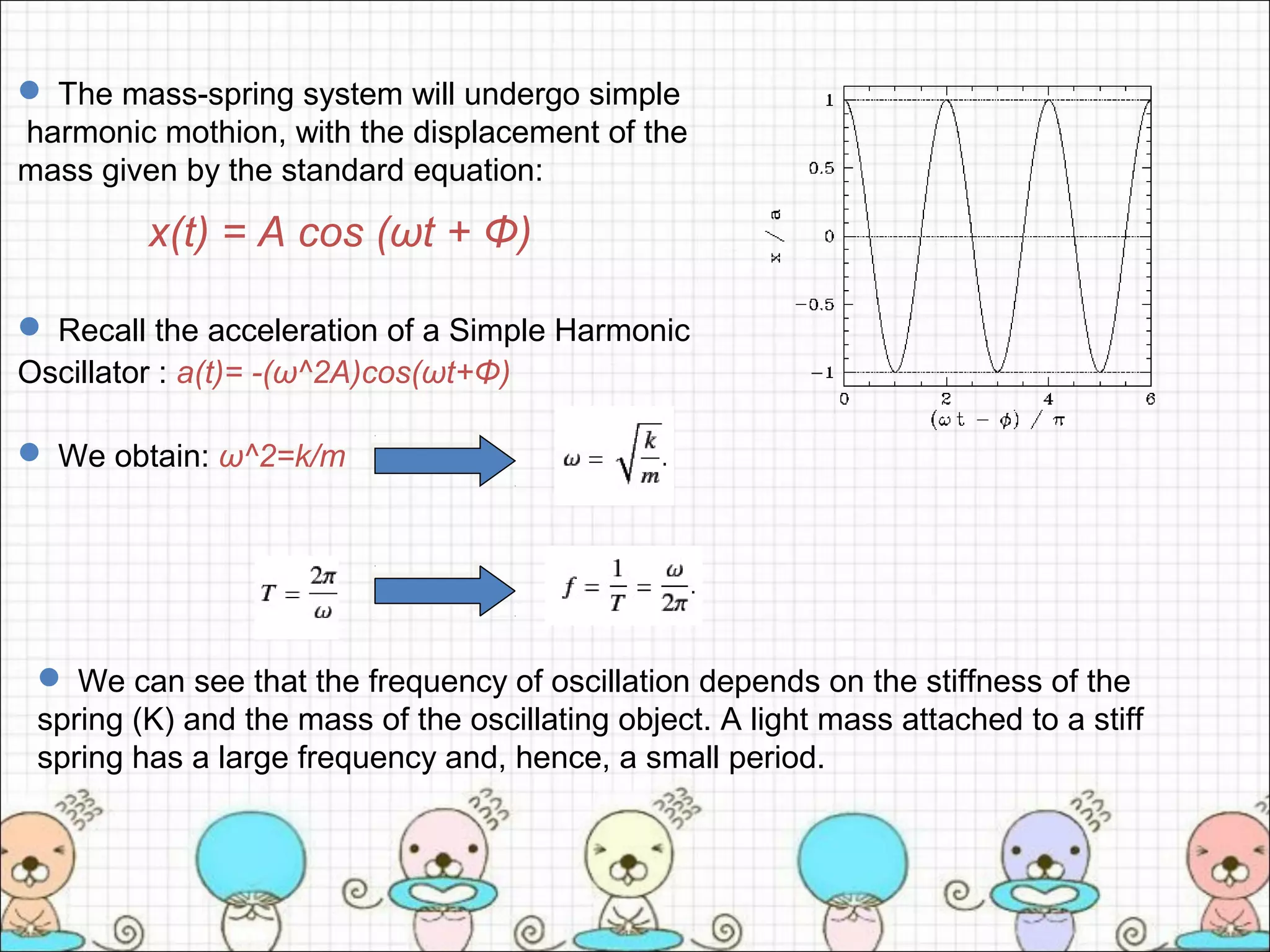- Using Newton's second law, F=ma, this results in the mass undergoing simple harmonic motion described by the equation x(t) = A cos(ωt + Φ), where the frequency

1. Horizontal Mass
Spring System
By: Yueyan Li
section: LE2
Learning objective 1

2.  Consider a compact mass m that slides
over a frictionless horizontal surface.
 Suppose that the mass is attached to
one end of a light horizontal spring whose
other end is anchored in an immovable wall.
 At time t , let x(t) be the extension of the
spring.
Note: the extension of the spring is the difference between the spring's actual length
and its unstretched length.
x(t) can also be used as a coordinate to determine the instantaneous horizontal
displacement of the mass.

3.  The equilibrium state of the system
corresponds to the situation in which
the mass is at rest, and the spring is
unextended.
 In this state, zero horizontal force acts
on the mass, and so there is no reason
for it to start to move.
 However, if the system is perturbed from its equilibrium state (i.e., if the mass is
displaced sideways, such that the spring becomes extended) then the mass
experiences a horizontal force given by Hooke's law,
f(x)= -kx

4. • f(x)= -kx
• Here, k>0 is the so-called force constant of the spring.
• The negative sign in the preceding expression indicates that f(x) is a restoring
force (i.e., if the displacement is positive then the force is negative, and vice
versa).
• The magnitude of this restoring force is directly proportional to the displacement
of the mass from its equilibrium position. Hooke's law only holds for relatively
small spring extensions.
• Newton's second law of motion leads to the following time evolution equation for
the system,
F = ma = -kx
a= -(k/m)x

5.  The mass-spring system will undergo simple
harmonic mothion, with the displacement of the
mass given by the standard equation:
x(t) = A cos (ωt + Φ)
 Recall the acceleration of a Simple Harmonic
Oscillator : a(t)= -(ω^2A)cos(ωt+Φ)
 We obtain: ω^2=k/m
 We can see that the frequency of oscillation depends on the stiffness of the
spring (K) and the mass of the oscillating object. A light mass attached to a stiff
spring has a large frequency and, hence, a small period.

6. Thank you !

7. Thank you !