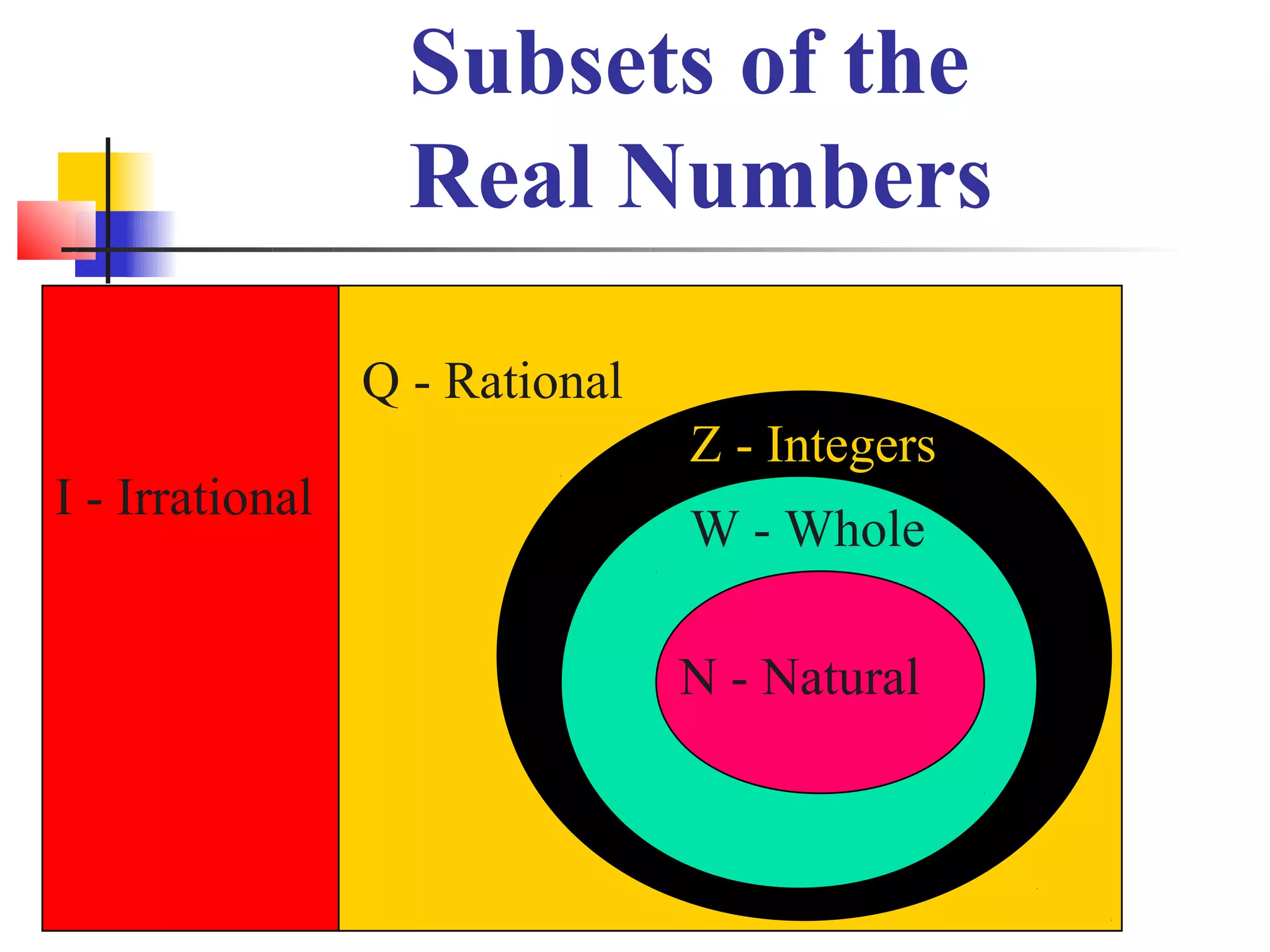
1. The document discusses real numbers and their properties, including subsets such as rational and irrational numbers. 2. Key topics covered include using a number line to graph and order real numbers, properties of number operations like closure and commutativity, and defining operations like addition, subtraction, multiplication and division. 3. Unit analysis is also introduced to check that units make sense when performing number operations for real-life applications.

1. 1-1 REAL NUMBERS
& NUMBER
OPERATIONS
Today’s Objectives:
I will use a number line to graph and
order real numbers.
I will identify properties of and use
operations with real numbers.

2. Number
Classifications
 Real:
 Rational: can be written as a ratio
(fractions: ½, ¼, 1/5)

Natural: counting #s
(1,2,3,4,5…)
 Whole: natural #s and 0
(0,1,2,3,4,5…)
 Integer: whole #’s and their opposites
(...-3,-2,-1,0,1,2,3…)
 Irrational: can not be written as a ratio because their
decimals do not terminate or repeat
 Imaginary:

3. Subsets of the
Real Numbers
Q - Rational
Z - Integers
I - Irrational
W - Whole
N - Natural

4. Classify each number
-1 real, rational, integer
6 real, rational, integer, whole,
natural
7 real, irrational
1
2 real, rational
0 real, rational, integer, whole
-2.222 real, rational

5. Number Lines
 Real #s can be pictured as points on a line called a
REAL NUMBER LINE .
 Numbers increase from left to right
 Point labeled 0 is the ORIGIN .
 The point on a # line that corresponds to a real # is
the GRAPH of the number.
 Drawing the point is called GRAPHING the
number or PLOTTING the point .
 The # that corresponds to a point on a line is the
COORDINATE of the point.

6. Ordering Real
Numbers
 A number line can be used to order real
numbers.
 The inequality symbols <, >, ≤, and ≥
can be used to show the order of two
numbers.

7. Decide which number is greater
using < or >. Then graph the
numbers on a number line.
1) 4 ___ 4/3 2) -3/2 ___ -11/3
0 0
– – – – –│ – – – – – – – – – –│ – – – – –
3) -2 ___ √2 4) -4.5 ___ -√24
0 0
– – – – –│ – – – – – – – – – –│ – – – – –

8. Properties of
Real Numbers
 Let a, b, and c be real numbers.
Property Addition Multiplication
Closure a + b is a real # ab is a real #
Commutative a+b=b+a ab = ba
Associative (a + b) + c = a + (b + c) (ab)c = a(bc)
Identity a+0=a a • 1 = a, 1 • a = a
Inverse a + (-a) = 0 a • 1/a = 1, a≠0
Distributive a(b + c) = ab + ac

9. Name the Property
1) 5 = 5+0 1) Additive Identity
2) 5(2 x +7) = 10x+35 2) Distributive
3) Commutative for
3) 8 • 7 = 7 • 8 Multiplication
4) (7+8)+2 = 2+(7+8) 4) Commutative for
Addition
5) 7+(8+2) = (7+8)+2
5) Associative for
6) 5 • 1/5 = 1 Addition
6) Multiplicative
Inverse

10. Operations with
Real Numbers
 Sum:
the answer to an addition problem
 Difference:
the answer to a subtraction problem
 Product:
the answer to a multiplication problem
 Quotient:
the answer to a division problem

11. Identifying
Properties of Real
Numbers
 The opposite, or additive inverse , of
any number a is –a.
 The reciprocal, or multiplicative
inverse , of any nonzero number a is 1/a.
 Subtraction is defined as adding the
opposite .
 Division is defined as multiplying by
the reciprocal .

12. Unit Analysis
 When you use the operations of addition,
subtraction, multiplication, and division in real
life, you should use unit analysis to check
that your units make sense.