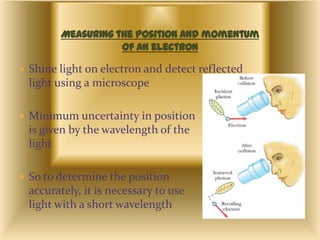
This document discusses the uncertainty principle as stated by Werner Heisenberg in 1927. It provides Heisenberg's background and contributions to physics. The principle states that the momentum and position of a particle cannot be simultaneously measured with perfect precision due to inherent uncertainties. There is a minimum for the product of the uncertainties in these two measurements. The document explains this concept and provides the formula for the uncertainty principle.