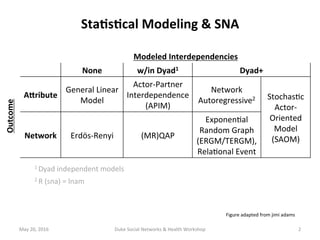
This document provides an introduction to Stochastic Actor-Oriented Models (SAOMs), also known as SIENA models. It discusses when SAOMs are appropriate to use, provides an overview of the general SAOM form, and covers key components like the network and behavior objective functions and rate functions. The presentation also outlines how SAOMs are estimated and fitted to data, provides an empirical example, and discusses extensions. SAOMs model how networks and behaviors change over time as actors make micro-level decisions to maximize their objective functions.