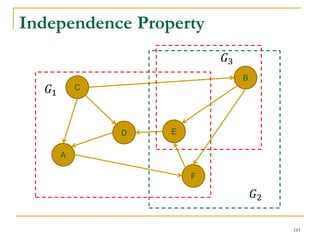
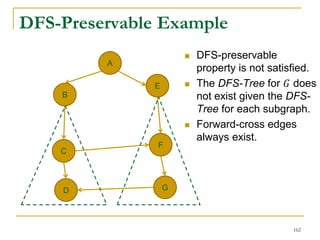
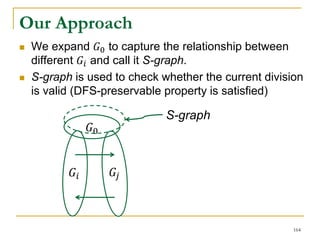
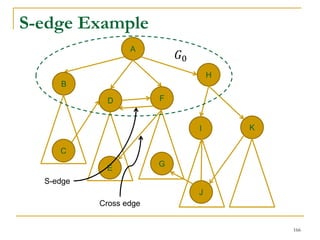
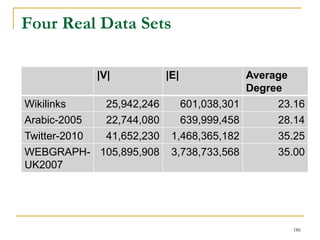
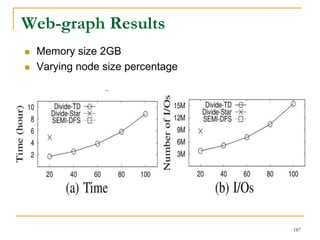
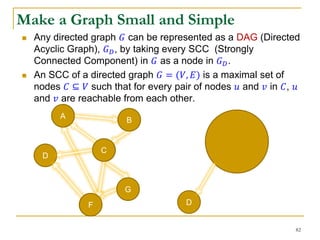
This document discusses influenceability estimation in social networks. It describes the independent cascade model of influence diffusion, where each node has an independent probability of influencing its neighbors. The problem is to estimate the expected number of nodes reachable from a given seed node. The document presents the naive Monte Carlo (NMC) approach, which samples possible graphs and averages the number of reachable nodes over the samples. While NMC provides an unbiased estimator, it has high variance. The document aims to reduce the variance to improve estimation accuracy.

1. Large Graph Processing
Jeffrey Xu Yu (于旭)
Department of Systems Engineering and
Engineering Management
The Chinese University of Hong Kong
yu@se.cuhk.edu.hk, http://www.se.cuhk.edu.hk/~yu

2. 2

3. Social Networks
3

4. Social Networks
4

5. Facebook Social Network
 In 2011, 721 million users, 69 billion friendship links. The
degree of separation is 4. (Four Degrees of Separation by
Backstrom, Boldi, Rosa, Ugander, and Vigna, 2012)
5

6. The Scale/Growth of Social Networks
 Facebook statistics
 829 million daily active users on average in June 2014
 1.32 billion monthly active users as of June 30, 2014
 81.7% of daily active users are outside the U.S. and
Canada
 22% increase in Facebook users from 2012 to 2013
 Facebook activities (every 20 minutes on Facebook)
 1 million links shared
 2 million friends requested
 3 million messages sent
http://newsroom.fb.com/company-info/
http://www.statisticbrain.com/facebook-statistics/
6

7. The Scale/Growth of Social Networks
 Twitter statistics
 271 million monthly active users in 2014
 135,000 new users signing up every day
 78% of Twitter active users are on mobile
 77% of accounts are outside the U.S.
 Twitter activities
 500 million Tweets are sent per day
 9,100 Tweets are sent per second
https://about.twitter.com/company
http://www.statisticbrain.com/twitter-statistics/
7

8. Location Based Social Networks
8

9. Financial Networks
 We borrow £1.7 trillion, but
we're lending £1.8 trillion.
Confused? Yes, inter-nation
finance is complicated..." 9

10. US Social Commerce --
Statistics and Trends
10

11. Activities on Social Networks
 When all functions are integrated ….
11

12. Graph Mining/Querying/Searching
 We have been working on many graph problems.
 Keyword search in databases
 Reachability query over large graphs
 Shortest path query over large graphs
 Large graph pattern matching
 Graph clustering
 Graph processing on Cloud
 ……
12

13. Part I: Social Networks
13

14. Some Topics
 Ranking over trust networks
 Influence on social networks
 Influenceability estimation in Social Networks
 Random-walk domination
 Diversified ranking
 Top-k structural diversity search
14

15. Ranking over Trust Networks
15

16.  Real rating systems (users and objects)
 Online shopping websites (Amazon) www.amazon.com
 Online product review websites (Epinions) www.epinions.com
 Paper review system (Microsoft CMT)
 Movie rating (IMDB)
 Video rating (Youtube)
Reputation-based Ranking
16

17. The Bipartite Rating Network
 Two entities: users and objects
 Users can give rating to objects
 If we take the average as the ranking score of an object,
o1 and o3 are the top.
 If we consider the user’s reputation, e.g., u4, …
Objects
Users
Ratings
17

18. Reputation-based Ranking
 Two fundamental problems
 How to rank objects using the ratings?
 How to evaluate users’ rating reputation?
 Algorithmic challenges
 Robustness
 Robust to the spamming users
 Scalability
 Scalable to large networks
 Convergence
 Convergent to a unique and fixed ranking vector
18

19. Signed/Unsigned Trust Networks
 Signed Trust Social Networks (users): A user can
express their trust/distrust to others by positive/negative
trust score.
 Epinions (www.epinions.com)
 Slashdot (www.slashdot.org)
 Unsigned Trust Social Networks (users): A user can only
express their trust.
 Advogato (www.advogato.org)
 Kaitiaki (www.kaitiaki.org.nz)
 Unsigned Rating Networks (users and objects)
 Question-Answer systems
 Movie-rating systems (IMDB)
 Video rating systems in Youtube
19

20. The Trustworthiness of a User
 The final trustworthiness of a user is determined by how
users trust each other in a global context and is
measured by bias.
 The bias of a user reflects the extend up to which his/her
opinions differ from others.
 If a user has a zero bias, then his/her opinions are 100%
unbaised and 100% taken.
 Such a user has high trustworthiness.
 The trustworthiness, the trust score, of a user is
1 – his/her bias score.
20

21. An Existing Approach
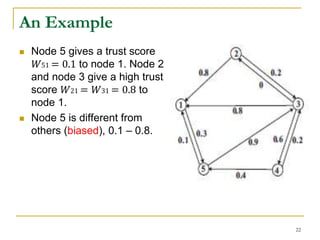
 MB [Mishra and Bhattacharya, WWW’11]
 The trustworthiness of a user cannot be trusted,
because MB treats the bias of a user by relative
differences between itself and others.
 If a user gives all his/her friends a much higher trust
score than the average of others, and gives all his/her
foes a much lower trust score than the average of
others, such differences cancel out. This user has
zero bias and can be 100% trusted.
21

22. An Example
 Node 5 gives a trust score
𝑊51 = 0.1 to node 1. Node 2
and node 3 give a high trust
score 𝑊21 = 𝑊31 = 0.8 to
node 1.
 Node 5 is different from
others (biased), 0.1 – 0.8.
22

23. MB Approach
 The bias of a node 𝑖 is 𝑏𝑖.
 The prestige score of node 𝑖 is 𝑟𝑖.
 The iterative system is
23

24. An Example
 Consider 51, 21, 31.
 A trust score = 0.1 – 0.8 = -0.7.
 Consider 23, 43, 53.
 A trust score = 0.9 – 0.2 = 0.7
 Node 5 has zero bias.
 The bias scores by MB.
24

25. Our Approach
 To address it, consider a contraction mapping.
 Given a metric space 𝑋 with a distance function 𝑑().
 A mapping 𝑇 from 𝑋 to 𝑋 is a contraction mapping if
there exists a constant c where 0 ≤ 𝑐 < 1 such that
𝑑(𝑇(𝑥), 𝑇(𝑦)) ≤ 𝑐 × 𝑑(𝑥, 𝑦).
 The 𝑇 has a unique fixed point.
25

26. Our Approach
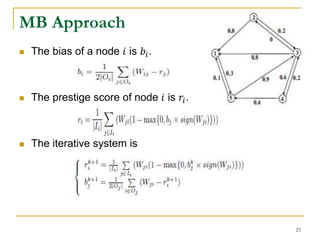
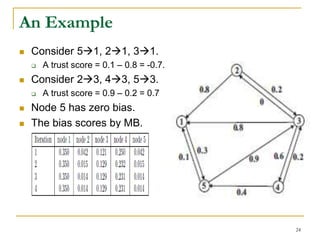
 We use two vectors, 𝑏 and 𝑟, for bias and prestige.
 The 𝑏𝑗 = (𝑓(𝑟)) 𝑗 denotes the bias of node 𝑗, where 𝑟 is
the prestige vector of the nodes, and 𝑓(𝑟) is a vector-
valued contractive function. (𝑓 𝑟 ) 𝑗 denotes the 𝑗-th
element of vector 𝑓(𝑟).
 Let 0 ≤ 𝑓(𝑟) ≤ 𝑒, and 𝑒 = [1, 1, … , 1] 𝑇
 For any 𝑥, 𝑦 ∈ 𝑅 𝑛, the function 𝑓: 𝑅 𝑛 → 𝑅 𝑛 is a vector-
valued contractive function if the following condition
holds,
𝑓 𝑥 – 𝑓 𝑦 ≤ 𝜆 ∥ 𝑥 − 𝑦 ∥∞ 𝑒
where 𝜆 ∈ [0,1) and ∥∙∥∞ denotes the infinity norm.
26

27. The Framework
 Use a vector-valued contractive function, which is a
generalization of the contracting mapping in the fixed
point theory.
 MB is a special case in our framework.
 The iterative system can converges into a unique fixed
prestige and bias vector in an exponential rate of
convergence.
 We can handle both unsigned and singed trust social
networks.
27

28. Influence on Social Networks
28

29. Diffusion in Networks
 We care about the decisions made by friends and
colleagues.
 Why imitating the behavior of others
 Informational effects: the choices made by others can
provide indirect information about what they know.
 Direct-benefit effects: there are direct payoffs from
copying the decisions of others.
 Diffusion: how new behaviors, practices, opinions,
conventions, and technologies spread through a social
network.
29

30. A Real World Example
 Hotmail’s viral climb to
the top spot (90’s):
8 million users in
18 months!
 Far more effective than
conventional advertising
by rivals and far cheaper
too!
30

31. Stochastic Diffusion Model
 Consider a directed graph 𝐺 = (𝑉, 𝐸).
 The diffusion of information (or influence) proceeds in
discrete time steps, with time 𝑡 = 0, 1, …. Each node 𝑣
has two possible states, inactive and active.
 Let 𝑆𝑡 ⊆ 𝑉 be the set of active nodes at time 𝑡 (active set
at time 𝑡). 𝑆0 is the seed set (the seeds of influence
diffusion).
 A stochastic diffusion model (with discrete time steps) for
a social graph 𝐺 specifies the randomized process of
generating active sets 𝑆𝑡 for all 𝑡 ≥ 1 given the initial 𝑆0.
 A progressive model is a model 𝑆𝑡−1 ⊆ 𝑆𝑡 for 𝑡 > 1.
31

32. Influence Spread
 Let Φ(𝑆0) be the final active set (eventually stable
active set) where 𝑆0 is the initial seed set.
 Φ(𝑆0) is a random set determined by the stochastic
process of the diffusion model.
 To maximize the expected size of the final active set.
 Let 𝔼(𝑋) denote the expected value of a random
variable 𝑋.
 The influence spreed of seed set 𝑆0 is defined as
𝜎 𝑆0 = 𝔼(|Φ(𝑆0)|). Here the expectation is taken
among all random events leading to Φ(𝑆0).
32

33. Independent Cascade Model (IC)
 IC takes 𝐺 = (𝑉, 𝐸), the influence probability 𝑝 on all
edges, and initial seed set 𝑆0 as the input, and generates
the active sets 𝑆𝑡 for all 𝑡 ≥ 1.
 At every time step 𝑡 ≥ 1, first set 𝑆𝑡 = 𝑆𝑡−1.
 Next for every inactive node 𝑣 ∉ 𝑆𝑡−1, for node 𝑢 ∈
𝑁𝑖𝑛 𝑣 ∩ 𝑆𝑡−1𝑆𝑡−2 , 𝑢 executes an activation attempt
with success probability 𝑝(𝑢, 𝑣). If successful, 𝑣 is
added into 𝑆𝑡 and it is said 𝑢 activates 𝑣 at time 𝑡. If
multiple nodes active 𝑣 at time 𝑡, the end effect is the
same.
33

34. An Example
34

35. Another Example
35

36. Influenceability Estimation in Social Networks
 Applications
 Influence maximization for viral marketing
 Influential nodes discovery
 Online advertisement
 The fundamental issue
 How to evaluate the influenceability for a give node
in a social network?
36

37.  The independent cascade model.
 Each node has an independent probability to
influence his neighbors.
 Can be modeled by a probabilistic graph, called
influence network, 𝐺 = (𝑉, 𝐸, 𝑃).
 A possible graph 𝐺 𝑃 = (𝑉𝑃, 𝐸 𝑃) has probability
Pr 𝐺 𝑃 = 𝑒∈𝐸 𝑃
𝑝 𝑒 𝑒∈𝐸 𝐸 𝑃
(1 − 𝑝 𝑒)
 There are 2|𝐸| possible graphs (Ω).
Reconsider IC Model
37

38. An Example
38

39.  Independent cascade model.
 Given a probabilistic graph 𝐺 𝑃 = (𝑉𝑃, 𝑉𝑃)
 Pr 𝐺 𝑃 = 𝑒∈𝐸 𝑃
𝑝 𝑒 𝑒∈𝐸 𝐸 𝑃
(1 − 𝑝 𝑒)
 Given a graph 𝐺 = (𝑉, 𝐸, 𝑃), and a node 𝑠, estimate the
expected number of nodes that are reachable from 𝑠.
 𝐹𝑠(𝐺) = 𝐺 𝑃∈Ω
Pr 𝐺 𝑃 𝑓𝑠(𝐺 𝑃) where 𝑓𝑠(𝐺 𝑃) is the
number of nodes that are reachable from the seed
node 𝑠.
The Problem
39

40. Reduce the Variance
 The accuracy of an approximate algorithm is measured
by the mean squared error 𝔼 ( 𝐹𝑠 𝐺 − 𝐹𝑠 𝐺 )2
 By the variance-bias decomposition
𝔼 ( 𝐹𝑠 𝐺 − 𝐹𝑠 𝐺 )2 = Var 𝐹𝑠 𝐺 + 𝔼( 𝐹𝑠 𝐺 − 𝐹𝑠 𝐺 )
2
 Make an estimator unbiased  the 2nd term will be
cancelled out.
 Make the variance as small as possible.
40

41. Naïve Monte-Carlo (NMC)
 Sampling 𝑁 possible graphs 𝐺1, 𝐺2, … , 𝐺 𝑁.
 For each sampled possible graph 𝐺𝑖, compute the
number of nodes that are reachable from 𝑠.
 𝑁𝑀𝐶 Estimator: Average of the number of reachable
nodes over 𝑁 possible graphs. 𝐹 𝑁𝑀𝐶 = 𝑖=1
𝑁
𝑓𝑠(𝐺 𝑖)
𝑁
 𝐹 𝑁𝑀𝐶 is an unbiased estimator of 𝐹𝑠(𝐺) since
𝔼 𝐹 𝑁𝑀𝐶 = 𝐹𝑠 𝐺 .
 𝑁𝑀𝐶 is the only existing algorithm used in the influence
maximization literature.
41

42. Naïve Monte-Carlo (NMC)
 𝑁𝑀𝐶 Estimator: Average of the number of reachable
nodes over 𝑁 possible graphs. 𝐹 𝑁𝑀𝐶 = 𝑖=1
𝑁
𝑓𝑠(𝐺 𝑖)
𝑁
 𝐹 𝑁𝑀𝐶 is an unbiased estimator of 𝐹𝑠(𝐺)
since 𝔼 𝐹 𝑁𝑀𝐶 = 𝐹𝑠(𝐺).
 The variance of 𝑁𝑀𝐶 is
𝑉𝑎𝑟 𝐹 𝑁𝑀𝐶 =
𝔼 𝑓𝑠(𝐺)2 − (𝔼 𝑓𝑠(𝐺) )2
𝑁
=
𝐺 𝑃∈Ω 𝑃𝑟 𝐺 𝑝 𝑓𝑠(𝐺)2−𝐹𝑠(𝐺)2
𝑁
 Computing the variance is extreme expensive, because
it needs to enumerate all the possible graphs.
42

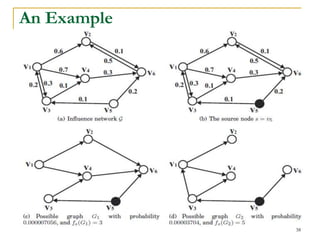
43. Naïve Monte-Carlo (NMC)
 In practice, it resorts to an unbiased estimator of 𝑉𝑎𝑟( 𝐹 𝑁𝑀𝐶).
 The variance of 𝑁𝑀𝐶 is
𝑉𝑎𝑟 𝐹 𝑁𝑀𝐶 =
𝑖=1
𝑁
(𝑓𝑠 𝐺𝑖 − 𝐹 𝑁𝑀𝐶)2
𝑁 − 1
 But, 𝑉𝑎𝑟 𝐹 𝑁𝑀𝐶 may be very large, because 𝑓𝑠 𝐺𝑖 fall into
the interval [0, 𝑛 − 1].
 The variance can be up to 𝑂(𝑛2).
43

44. Stratified Sampling
 Stratified is to divide a set of data items into subsets
before sampling.
 A stratum is a subset.
 The strata should be mutually exclusive, and should
include all data items in the set.
 Stratified sampling can be used to reduce variance.
44

45. A Recursive Estimator [Jin et al. VLDB’11]
 Randomly select 1 edge to partition the probability
space (the set of all possible graphs) into 2 strata
(2 subsets)
 The possible graphs in the first subset include
the selected edge.
 The possible graphs in the second subset do
not include the selected edge.
 Sample possible graphs in each stratum 𝑖 with a
sample size 𝑁𝑖 proportioning to the probability of
that stratum.
 Recursively apply the same idea in each stratum.
45

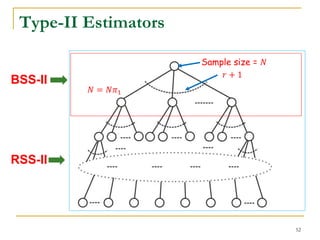
46. A Recursive Estimator [Jin et al. VLDB’11]
 Advantages:
 unbiased estimator with a smaller variance.
 Limitations:
 Select only one edge for stratification, which is not
enough to significantly reduce the variance.
 Randomly select edges, which results in a possible
large variance.
46

47. More Effective Estimators
 Four Stratified Sampling (SS) Estimators
 Type-I basic SS estimator (BSS-I)
 Type-I recursive SS estimator (RSS-I)
 Type-II basic SS estimator (BSS-II)
 Type-II recursive SS estimator (RSS-II)
 All are unbiased and their variances are significantly
smaller than the variance of NMC.
 Time and space complexity of all are the same as
NMC.
47

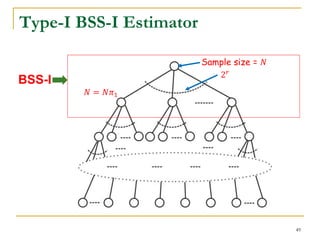
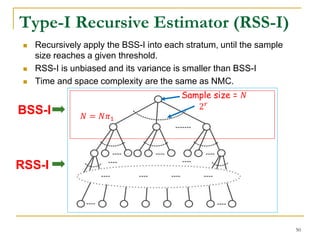
48. Type-I Basic Estimator (BSS-I)
 Select 𝑟 edges to partition the probability space (all the
possible graphs) into 2 𝑟
strata.
 Each stratum corresponds to a probability subspace
(a set of possible graphs).
 Let 𝜋𝑖 = Pr[𝐺 𝑃 ∈ Ω𝑖].
 How to select 𝑟 edges: BFS or random
48

49. Type-I BSS-I Estimator
Sample size = 𝑁
2 𝑟
𝑁 = 𝑁𝜋1
BSS-I
49

50. Type-I Recursive Estimator (RSS-I)
 Recursively apply the BSS-I into each stratum, until the sample
size reaches a given threshold.
 RSS-I is unbiased and its variance is smaller than BSS-I
 Time and space complexity are the same as NMC.
Sample size = 𝑁
BSS-I
RSS-I
𝑁 = 𝑁𝜋1
50

51. Type-II Basic Estimator (BSS-II)
 Select 𝑟 edges to partition the probability space (all the
possible graphs) into 𝑟 + 1 strata.
 Similarly, each stratum corresponds to a probability
subspace (a set of possible graphs).
 How to select 𝑟 edges: BFS or random
51

52. Type-II Estimators
Sample size = 𝑁
𝑟 + 1
BSS-II
RSS-II
𝑁 = 𝑁𝜋1
52

53. Random-walk Domination
53

54.  Social browsing: a process that users in a social network find
information along their social ties.
 photo-sharing Flickr, online advertisements
 Two issues:
 Problem-I: How to place items on 𝑘 users in a social
network so that the other users can easily discover by
social browsing?
 To minimize the expected number of hops that every
node hits the target set.
 Problem-II: How to place items on 𝑘 users so that as many
users as possible can discover by social browsing?
 To maximize the expected number of nodes that hit the
target set.
Social Browsing
54

55.  The two problems are a random walk problem.
 𝐿-length random walk model where the path length of
random walks is bounded by a nonnegative number 𝐿.
 A random walk in general can be considered as 𝐿 = ∞.
 Let 𝑍 𝑢
𝑡
be the position of an 𝐿-length random walk,
starting from node 𝑢, at discrete time 𝑡.
 Let 𝑇𝑢𝑣
𝐿 be a random walk variable.
 𝑇𝑢𝑣
𝐿
≜ min{min 𝑡: 𝑍 𝑢
𝑡
= v, t ≥ 0}, 𝐿
 The hitting time ℎ 𝑢𝑣
𝐿 can be defined as the expectation
of 𝑇𝑢𝑣
𝐿 .
 ℎ 𝑢𝑣
𝐿
= 𝔼[𝑇𝑢𝑣
𝐿
]
The Random Walk
55

56. The Hitting Time
 Sarkar and Moore in UAI’07 define the hitting time of the
𝐿-length random walk in a recursive manner.
ℎ 𝑢𝑣
𝐿 =
0, 𝑢 = 𝑣
1 +
𝑤∈𝑉
𝑝 𝑢𝑤ℎ 𝑤𝑣
𝐿−1, 𝑢 ≠ 𝑣
 Our hitting time can be computed by the recursive
procedure.
 Let 𝑑 𝑢 be the degree of node 𝑢 and 𝑁(𝑢) be the set of
neighbor nodes of 𝑢.
 𝑝 𝑢𝑤 = 1/𝑑 𝑢 be the transition probability for 𝑤 ∈
𝑁(𝑢) and 𝑝 𝑢𝑤 = 0 otherwise.
56

57. The Random-Walk Domination
 Consider a set of nodes 𝑆. If a random walk from 𝑢
reaches 𝑆 by an 𝐿-length random walk, we say
𝑆 dominates 𝑢 by an 𝐿-length random walk.
 Generalized hitting time over a set of nodes, 𝑆. The
hitting time ℎ 𝑢𝑆
𝐿
can be defined as the expectation of a
random walk variable 𝑇𝑢𝑆
𝐿
.
 𝑇𝑢𝑆
𝐿
≜ min{min 𝑡: 𝑍 𝑢
𝑡
∈ 𝑆, t ≥ 0}, 𝐿
 ℎ 𝑢𝑆
𝐿
= 𝔼[𝑇𝑢𝑆
𝐿
]
 It can be computed recursively.
 ℎ 𝑢𝑆
𝐿
=
0, 𝑢 ∈ 𝑆
1 + 𝑤∈𝑉 𝑝 𝑢𝑤ℎ 𝑤𝑆
𝐿−1
, 𝑢 ∉ 𝑆
57

58.  How to place items on 𝑘 users in a social network so that
the other users can easily discover by social browsing?
 To minimize the total expected number of hops of which
every node hits the target set.
Problem-I
or
58

59.  How to place items on 𝑘 users so that as many users as
possible can discover by social browsing? To maximize the
expected number of nodes that hit the target set.
 Let 𝑋 𝑢𝑆
𝐿
be an indicator random variable such that if 𝑢 hits
any one node in 𝑆, then 𝑋 𝑢𝑆
𝐿
= 1, and 𝑋 𝑢𝑆
𝐿
= 0 otherwise by an
𝐿-length random walk.
 Let 𝑝 𝑢𝑆
𝐿
be the probability of an event that an 𝐿-length random
walk starting from 𝑢 hits a node in 𝑆.
 Then, 𝔼 𝑋 𝑢𝑆
𝐿
= 𝑝 𝑢𝑆
𝐿
.
 𝑝 𝑢𝑆
𝐿
=
1, 𝑢 ∈ 𝑆
𝑤∈𝑉 𝑝 𝑢𝑤 𝑝 𝑤𝑆
𝐿−1
, 𝑢 ∉ 𝑆
Problem-II
59

60. Influence Maximization vs Problem II
 Influence maximization is to select 𝑘 nodes to maximize
the expected number of nodes that are reachable from
the nodes selected.
 Independent cascade model
 Probability associated with the edges are independent
 A target node can influence multiple immediate neighbors
at a time.
 Problem II is to select 𝑘 nodes to maximize the
expected number of nodes that reach a node in the
nodes selected.
 𝐿-length random walk model
60

61.  The submodular set function maximization subject to
cardinality constraint is 𝑁𝑃-hard.

𝑎𝑟𝑔 max
𝑆⊆𝑉
𝐹(𝑆)
𝑠. 𝑡. 𝑆 = 𝐾
 The greedy algorithm
 There is a 1 −
1
𝑒
approximation algorithm.
 Linear time and space complexity w.r.t. the size of the
graph.
 Submodularity: 𝐹(𝑆) is submodular and non-decreasing.
 Non-decreasing: 𝑓(𝑆) ≤ 𝑓(𝑇) for 𝑆 ⊆ 𝑇 ⊆ 𝑉.
 Submodular: Let 𝑔𝑗(𝑆) = 𝑓(𝑆 ∪ {𝑗}) – 𝑓(𝑆) be the marginal gain. Then,
𝑔𝑗(𝑆) ≥ 𝑔𝑗(𝑇), for j ∈ V T and 𝑆 ⊆ 𝑇 ⊆ 𝑉.
Submodular Function Maximization
61

62.  The submodular set function maximization subject to
cardinality constraint is 𝑁𝑃-hard.

𝑎𝑟𝑔 max
𝑆⊆𝑉
𝐹(𝑆)
𝑠. 𝑡. 𝑆 = 𝐾
 Both Problem I and Problem II use a submodular set
function.
 Problem-I: 𝐹1 S = nL − 𝑢∈𝑉𝑆 ℎ 𝑢𝑆
𝐿
 Problem-II: 𝐹2(𝑆) = 𝑤∈𝑉 𝔼[𝑋 𝑤𝑆
𝐿
] = 𝑤∈𝑉 𝑝 𝑤𝑆
𝐿
Submodular Function Maximization
62

63. The Algorithm
 Let 𝜎 𝑢 S = F(𝑆 ∪ {𝑢}) − 𝐹(𝑆)
 It implies dynamic programming (DP) is needed to
compute the marginal gain.
Marginal gain
63

64. Diversified Ranking
64

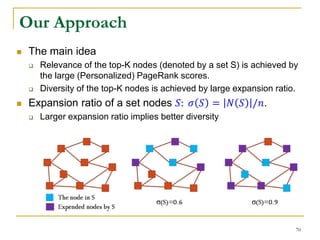
65. Diversified Ranking [Li et al, TKDE’13]
 Why diversified ranking?
 Information requirements diversity
 Query incomplete
PAKDD09-65

66. Problem Statement
 The goal is to find K nodes in a graph that are relevant to
the query node, and also they are dissimilar to each
other.
 Main applications
 Ranking nodes in social network, ranking papers, etc.
66

67. Challenges
 Diversity measures
 No wildly accepted diversity measures on graph in the
literature.
 Scalability
 Most existing methods cannot be scalable to large
graphs.
 Lack of intuitive interpretation.
67

68. Grasshopper/ManiRank
 The main idea
 Work in an iterative manner.
 Select a node at one iteration by random walk.
 Set the selected node to be an absorbing node, and
perform random walk again to select the second node.
 Perform the same process 𝐾 iterations to get 𝐾 nodes.
 No diversity measure
 Achieving diversity only by intuition and experiments.
 Cannot scale to large graph (time complexity O(𝐾𝑛2
))
68

69. Grasshopper/ManiRank
 Initial random walk with no absorbing states
 Absorbing random walk after ranking the first item
69

70. Our Approach
 The main idea
 Relevance of the top-K nodes (denoted by a set S) is achieved by
the large (Personalized) PageRank scores.
 Diversity of the top-K nodes is achieved by large expansion ratio.
 Expansion ratio of a set nodes 𝑆: 𝜎 𝑆 = 𝑁 𝑆 /𝑛.
 Larger expansion ratio implies better diversity
70

71.  The submodular set function maximization subject to
cardinality constraint is 𝑁𝑃-hard.

𝑎𝑟𝑔 max
𝑆⊆𝑉
𝐹(𝑆)
𝑠. 𝑡. 𝑆 = 𝐾
 The greedy algorithm
 There is a 1 −
1
𝑒
approximation algorithm.
 Linear time and space complexity w.r.t. the size of the
graph.
 Submodularity: 𝐹(𝑆) is submodular and non-decreasing.
 Non-decreasing: 𝑓(𝑆) ≤ 𝑓(𝑇) for 𝑆 ⊆ 𝑇 ⊆ 𝑉.
 Submodular: Let 𝑔𝑗(𝑆) = 𝑓(𝑆 ∪ {𝑗}) – 𝑓(𝑆) be the marginal gain. Then,
𝑔𝑗(𝑆) ≥ 𝑔𝑗(𝑇), for j ∈ V T and 𝑆 ⊆ 𝑇 ⊆ 𝑉.
Submodular Function Maximization
71

72. Top-k Structural Diversity
Search
72

73.  Social contagion is a process of information (e.g. fads,
news, opinions) diffusion in the online social networks
 Traditional biological contagion model, the affected
probability depends on degree.
MarketingOpinions Diffusion Social Network
Social Contagion
73

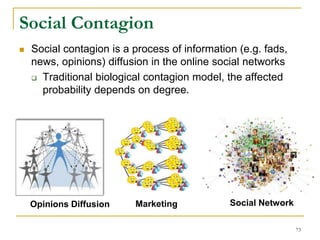
74. Facebook Study [Ugander et al., PNAS’12]
 Case study: The process of a user joins Facebook in
response to an invitation email from an existing
Facebook user.
 Social contagion is not like biological contagion.
74

75.  Structural diversity of an
individual is the number of
connected components in
one’s neighborhood.
 The problem: Find 𝑘
individuals
with highest structural
diversity. Connected components in the
neighborhood of “white center”
Structural Diversity
75

76. Part II: I/O Efficiency
76

77. Big Data: The Volume
 Consider a dataset 𝐷 of 1 PetaByte (1015 bytes).
A linear scan of 𝐷 takes 46 hours with a fastest
Solid State Drive (SSD) of speed of 6GB/s.
 PTIME queries do not always serve as a good yardstick
for tractability in “Big Data with Preprocessing” by Fan.
et al., PVLDB”13.
 Consider a function 𝑓 𝐺 . One possible way is to
make 𝐺 small to be 𝐺’, and find the answers from
𝐺’ as it can be answered by 𝐺, 𝑓’(𝐺’) ≈ 𝑓(𝐺).
 There are many ways we can explore.
77

78. Big Data: The Volume
 Consider a function 𝑓 𝐺 . One possible way is to make 𝐺
small to be 𝐺’, and find the answers from 𝐺’ as it can be
answered by 𝐺, 𝑓’(𝐺’) ≈ 𝑓(𝐺).
 There are many ways we can explore.
 Make data simple and small
 Graph sampling, Graph compression
 Graph sparsification, Graph simplification
 Graph summary
 Graph clustering
 Graph views
78

79. More Work on Big Data
 We also believe that there are many things we need to
do on Big Data.
 We are planning explore many directions.
 Make data simple and small
 Graph sampling, graph simplification, graph
summary, graph clustering, graph views.
 Explore different computing approaches
 Parallel computing, distributed computing,
streaming computing, semi-external/external
computing.
79

80. I/O Efficient Graph Computing
 I/O Efficient: Computing SCCs in Massive Graphs by
Zhiwei Zhang, Jeffrey Xu Yu, Lu Qin, Lijun Chang, and
Xuemin Lin, SIGMOD’13.
 Contract & Expand: I/O Efficient SCCs Computing by
Zhiwei Zhang, Lu Qin, and Jeffrey Xu Yu.
 Divide & Conquer: I/O Efficient Depth-First Search,
Zhiwei Zhang, Jeffrey Xu Yu, Lu Qin, and Zechao
Shang.
80

81. Reachability Query
 Two possible but infeasible solutions:
 Traverse 𝐺(𝑉, 𝐸) to answer a reachability query
 Low query performance: 𝑂(|𝐸|) query time
 Precompute and store the transitive closure
 Fast query processing
 Large storage requirement: 𝑂(|𝑉|2)
 The labeling approaches:
 Assign labels to nodes in a
preprocessing step offline.
 Answer a query using the labels
assigned online.
81

82. A
B
D
C
F
G
A
B
C
G
F D
Make a Graph Small and Simple
 Any directed graph 𝐺 can be represented as a DAG (Directed
Acyclic Graph), 𝐺 𝐷, by taking every SCC (Strongly
Connected Component) in 𝐺 as a node in 𝐺 𝐷.
 An SCC of a directed graph 𝐺 = (𝑉, 𝐸) is a maximal set of
nodes 𝐶 ⊆ 𝑉 such that for every pair of nodes 𝑢 and 𝑣 in 𝐶, 𝑢
and 𝑣 are reachable from each other.
82

83. A
B
D
C
I
E
F
G
H
A
B
C
G
F
D
E
H
I
The Reachability Queries
 Reachability queries can be answered by DAG.
83

84. The Issue and the Challenge
 It needs to convert a
massive directed graph 𝐺
into a DAG 𝐺 𝐷 in order to
process it efficiently
because
 𝐺 cannot be held in main
memory, and 𝐺 𝐷 can be
much smaller.
 It is assumed that it can be
done in the existing works.
 But, it needs a large
main memory to convert.
84

85. The Issue and the Challenge
 The Dataset uk-2007
 Nodes: 105,896,555
 Edges: 3,738,733,648
 Average degree: 35
 Memory:
 400 MB for nodes, and
 28 GB for edges.
85

86. In Memory Algorithm?
 In Memory Algorithm: Scan 𝐺 twice
 DFS(G) to obtain a decreasing order for each node of 𝐺
 Reverse every edge to obtain 𝐺 𝑇, and
 DFS(𝐺 𝑇) according to the same decreasing order to find all
SCCs.
86

87. 4
7
2 3
51
9
68
In Memory Algorithm?
 DFS(G) to obtain a decreasing order for each node of 𝐺
87

88. 4
7
2 3
51
9
68
4
7
2 3
51
9
68
In Memory Algorithm?
 Reverse every edge to obtain 𝐺 𝑇
.
88

89. 4
7
2 3
51
9
68
In Memory Algorithm?
 DFS(𝐺 𝑇
) according to the same decreasing order to find all
SCCs. (A subtree (in black edges) form an SCC.)
89

90. (Semi)-External Algorithms
 In Memory Algorithm: Scan 𝐺 twice
 The in memory algorithm cannot handle a large graph that
cannot be held in memory.
 Why? No locality. A large number of random I/Os.
 Consider external algorithms and/or semi-external
algorithms. Let 𝑀 be the size of main memory.
 External algorithm: 𝑀 < |𝐺|
 Semi-external algorithm: 𝑘 ∙ |𝑉| ≤ 𝑀 < |𝐺|
 It assumes that a tree can be held in memory.
90

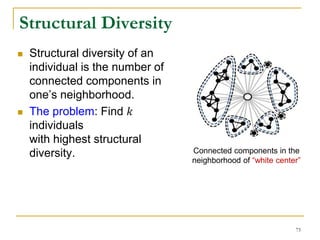
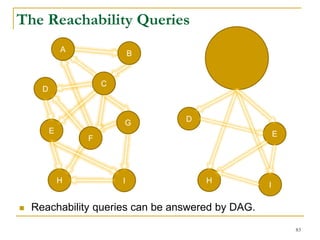
91. A
B
D
C
I
E
F
G
H
A
B
C
G
F
Main Memory
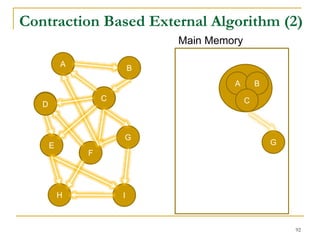
Contraction Based External Algorithm (1)
 Load in a subgraph and merge SCCs
in it in main memory in every iteration
[Cosgaya-Lozano et al. SEA'09]
91

92. A
B
D
C
I
E
F
G
H
A
B
C
G
F
A B
C
G
D
Main Memory
Contraction Based External Algorithm (2)
92

93. A
B
D
C
I
E
F
G
H
A
B
C
G
F
A B
C GD FD
H
E
Cannot Find All SCCs Always!
Main Memory
DAG! And memory is full!Cannot load in “I” into memory!
Contraction Based External Algorithm (3)
93

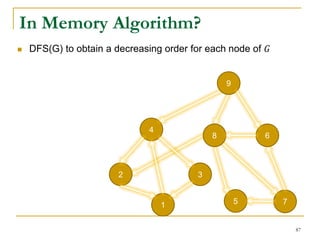
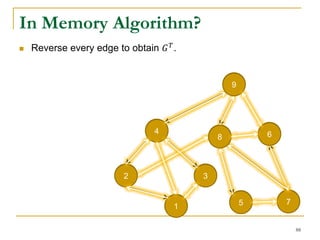
94. 2
8
3
4
7
5
1
9
6
Tree-Edge
Forward-Cross-Edge
Backward-Edge
Forward-Edge
Backward-Cross-Edgedelete old tree edge
New tree edge
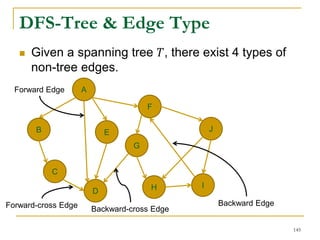
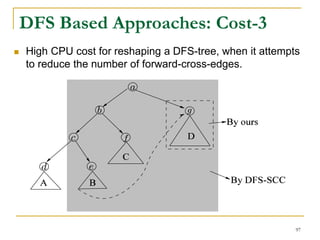
DFS Based Semi-External Algorithm
 Find a DFS-tree without
forward-cross-edges
[Sibeyn et al. SPAA’02].
 For a forward-cross-
edge (𝑢, 𝑣), delete tree
edge to 𝑣, and (𝑢, 𝑣) as
a new tree edge.
94

95. DFS Based Approaches: Cost-1
 DFS-SCC uses sequential I/Os.
 DFS-SCC needs to traverse a graph 𝐺 twice using DFS
to compute all SCCs.
 In each DFS, in the worst case it needs the number of
𝑑𝑒𝑝𝑡ℎ(𝐺) ∙ |𝐸(𝑉)|/𝐵 I/Os, where 𝐵 is the block size.
95

96. DFS Based Approaches: Cost-2
 Partial SCCs cannot be contracted to save space while
constructing a DFS tree.
 Why?
 DFS-SCC needs to traverse a graph 𝐺 twice using DFS to
compute all SCCs.
 DFS-SCC uses a total order of nodes (decreasing postorder)
in the second DFS, which is computed in the first DFS.
 SCCs cannot be partially contracted in the first DFS.
 SCCs can be partially contracted in the second DFS, but we
have to remember which nodes belongs to which SCCs with
extra space. Not free!
96

97. DFS Based Approaches: Cost-3
 High CPU cost for reshaping a DFS-tree, when it attempts
to reduce the number of forward-cross-edges.
97

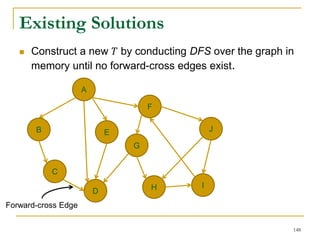
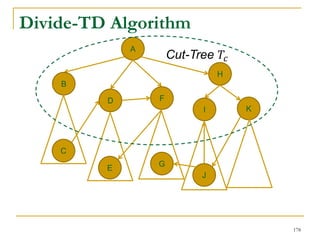
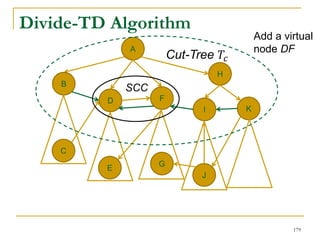
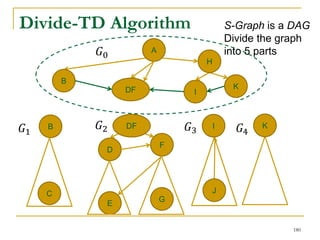
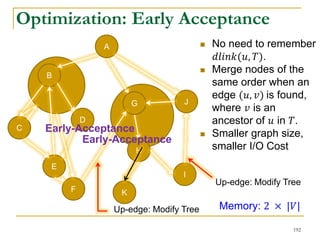
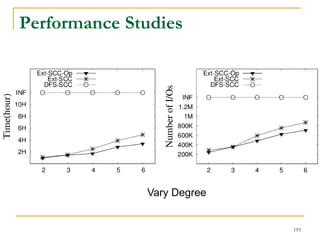
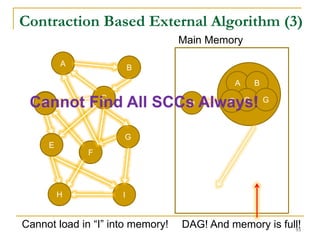
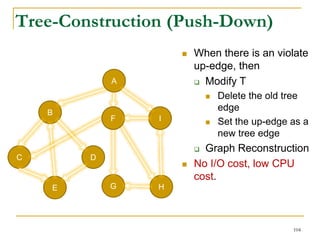
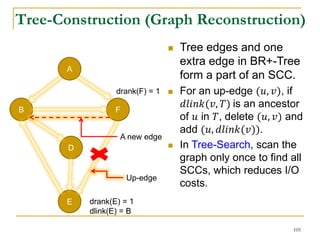
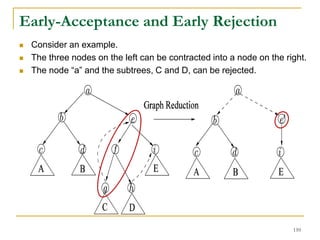
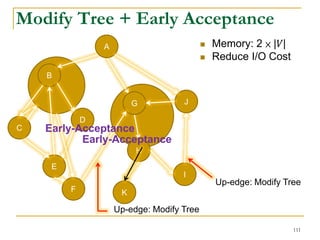
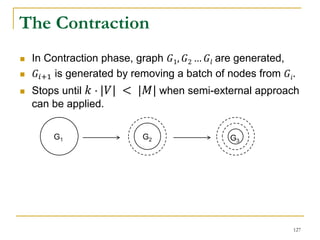
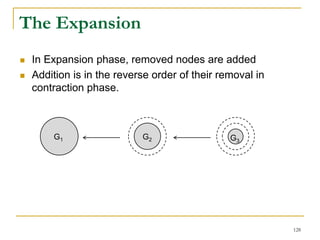
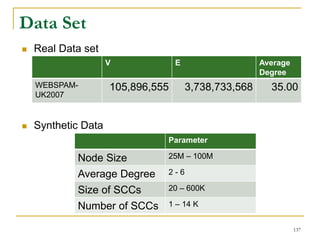
98. Our New Approach [SIGMOD’13]
 We propose a new two phase algorithm, 2P-SCC:
 Tree-Construction and Tree-Search.
 In Tree-Construction phase, we construct a tree-like
structure.
 In Tree-Search phase, we scan the graph only once.
 We further propose a new algorithm, 1P-SCC, to
combine Tree-Construction and Tree-Search with new
optimization techniques, using a tree.
 Early-Acceptance
 Early-Rejection
 Batch Edge Reduction
A joint work by Zhiwei Zhang, Jeffrey Yu, Qin Lu, Lijun Chang, and Xuemin Lin
98

99. A New Weak Order
 The total order used in DFS-SCC is too strong and there
is no obvious relationship between the total order and
the SCCs per se, in order to reduce I/Os.
 The total order cannot help to reduce I/O costs.
 We introduce a new weak order.
 For an SCC, there must exist at least one cycle.
 While constructing a tree 𝑇 for 𝐺, a cycle will appear to
contain at least one edge (𝑢, 𝑣) that links to a higher
level node in 𝑇. 𝑑𝑒𝑝𝑡ℎ(𝑢) > 𝑑𝑒𝑝𝑡ℎ(𝑣).
 There are two cases when 𝑑𝑒𝑝𝑡ℎ(𝑢) > 𝑑𝑒𝑝𝑡ℎ(𝑣).
 A cycle: 𝑣 is an ancestor of 𝑢 in 𝑇
 Not a cycle (up-edge): 𝑣 is not an ancestor of 𝑢 in 𝑇.
 We reduce the number of up-edges iteratively.
99

100.  Let 𝑅𝑠𝑒𝑡(𝑢, 𝐺, 𝑇) be the set of nodes including 𝑢 and nodes that
𝑣 can reach by a tree 𝑇 of 𝐺.
 𝑑𝑒𝑝𝑡ℎ(𝑢, 𝑇): The length of the longest simple
path from root to 𝑢.
 𝑑𝑟𝑎𝑛𝑘(𝑢, 𝑇) = min{𝑑𝑒𝑝𝑡ℎ(𝑣, 𝑇) | 𝑣 ∈ 𝑅𝑠𝑒𝑡(𝑢, 𝐺, 𝑇)}
 drank is used as the weak order!
 𝑑𝑙𝑖𝑛𝑘 𝑢, 𝑇 = 𝑎𝑟𝑔𝑚𝑖𝑛 𝑣 𝑑𝑒𝑝𝑡ℎ 𝑣, 𝑇 𝑣 ∈ 𝑅𝑠𝑒𝑡(𝑢, 𝐺, 𝑇)}
 Nodes do not need to have a unique order.
B
H
C
D
G
E
A
IF
 depth(B) = 1
 drank(B) = 1
 dlink(B) = B
 depth(E) = 3
 drank(E) = 1
 dlink(E) = B
The Weak Order: drank
100

101. 2P-SCC
 To reduce Cost-1, we use a BR+-tree to compute all
SCCs in the Tree-Construction phase. We compute all
SCCs by traversing 𝐺 only once using the BR+-tree
constructed in the Tree-Search phase.
 To reduce Cost-3, we have shown that we only need to
update the depth of nodes locally.
101

102. B
H
C D
G
E
A
IF
 BR-Tree is a spanning
tree of G.
 BR+-Tree is a BR-Tree
plus some additional
edges (𝑢, 𝑣) such that 𝑣
is an ancestor of 𝑢.
BR-Tree and BR+-Tree
 In Memory: Black edges
102

103. B
H
C D
GE
A
IF
drank(I) = 1
drank(H) = 2
Up-edge
Tree-Construction: Up-edge
 An edge (𝑢, 𝑣) is an up-edge on
the conditions:
 𝑣 is not an ancestor of 𝑢 in 𝑇
 𝑑𝑟𝑎𝑛𝑘(𝑢, 𝑇) ≥ 𝑑𝑟𝑎𝑛𝑘(𝑣, 𝑇)
 Up-edges violate the existing
order
103

104.  When there is an violate
up-edge, then
 Modify T
 Delete the old tree
edge
 Set the up-edge as a
new tree edge
 Graph Reconstruction
 No I/O cost, low CPU
cost.
B
H
C D
GE
A
IF
Tree-Construction (Push-Down)
104

105. B
D
E
A
F
drank(E) = 1
dlink(E) = B
drank(F) = 1
Up-edge
Tree-Construction (Graph Reconstruction)
 Tree edges and one
extra edge in BR+-Tree
form a part of an SCC.
 For an up-edge (𝑢, 𝑣), if
𝑑𝑙𝑖𝑛𝑘(𝑣, 𝑇) is an ancestor
of 𝑢 in 𝑇, delete (𝑢, 𝑣) and
add (𝑢, 𝑑𝑙𝑖𝑛𝑘(𝑣)).
 In Tree-Search, scan the
graph only once to find all
SCCs, which reduces I/O
costs.
A new edge
105

106. Tree-Construction
 When a BR+-tree is completely constructed, there are no
up-edges.
 There are only two kinds of edges in G.
 The BR+-tree edges, and
 The edges (𝑢, 𝑣) where 𝑑𝑟𝑎𝑛𝑘(𝑢, 𝑇) < 𝑑𝑟𝑎𝑛𝑘(𝑣, 𝑇).
 Such edges do not play in any role in determining an
SCC.
106

107. B
H
C D
G
E
A
IF
In memory for each node u:
 TreeEdge(u)
 dlink(u)
 drank(u)
In total: 3 × |𝑉|
Search Procedure:
 If an edge (𝑢 , 𝑣) points
to an ancestor, merge
all nodes from 𝑣 to 𝑢 in
the tree
Only need to scan the
graph once.
Tree-Search
107

108. From 2P-SCC To 1P-SCC
 With 2P-SCC:
 In Tree-Construction phase, we construct a tree by an
approach similar to DFS-SCC, and
 In Tree-Search phase, we scan the graph only once.
 The memory used for BR+-tree is 3 × |𝑉|.
 With 1P-SCC: We combine Tree-Construction and Tree-
Search with new optimization techniques to reduce Cost-2
and Cost-3:
 Early-Acceptance
 Early-Rejection
 Batch Edge Reduction
 Only need to use a BR-tree with memory of 2 × |𝑉|.
108

109. Early-Acceptance and Early Rejection
 Early acceptance: we contract a partial SCC into a
node in an early stage while constructing a BR-tree.
 Early rejection: we identify necessary conditions to
remove nodes that will not participate in any SCCs
while constructing a BR-tree.
109

110. Early-Acceptance and Early Rejection
 Consider an example.
 The three nodes on the left can be contracted into a node on the right.
 The node “a” and the subtrees, C and D, can be rejected.
110

111. B
I
C
D
H
E
A
JG
 Memory: 2 × |𝑉|
 Reduce I/O Cost
KF
Up-edge: Modify Tree
Up-edge: Modify Tree
Early-Acceptance
Early-Acceptance
Modify Tree + Early Acceptance
111

112. DFS Based vs Ours Approaches
 I/O cost for DFS is high
 Use a total order
 Cannot merge SCCs
when found earlier
 Total order cannot be
changed. Large # of
I/Os.
 Cannot prune non-SCC
nodes
 Total order cannot be
changed
 Smaller I/O Cost
 Use a weaker order
 Merge SCCs as early as
possible
 Merge nodes with the
same order. Small size,
small # of I/Os.
 prune non-SCC nodes as
early as possible
 Weaker order is flexible
112

113. Optimization: Batch Edge Reduction
 With 1PC-SCC, CPU cost is still high.
 In order to determine whether (𝑢, 𝑣) is a backward-
edge/up-edge, it needs to check the ancestor
relationships between 𝑢 and 𝑣 over a tree.
 The tree is frequently updated.
 The average depth of nodes in the tree becomes
larger with frequently push-down operation.
113

114. Optimization: Batch Edge Reduction
 When memory can hold more edges, there is no need to
contract partial SCCs edge by edge.
 Find all SCCs in the main memory at the same time
 Read all edges that can be read into memory.
 Construct a graph with the edges of the tree
constructed in memory already plus the edges newly
read into memory.
 Construct a DAG in memory using the existing memory
algorithm, which finds all SCCs in memory.
 Reconstruct the BR-Tree according to the DAG.
114

115. Performance Studies
 Implement using visual C++ 2005
 Test on a PC with Intel Core2 Quard 2.66GHz CPU
and 3.43GB memory running Windows XP
 Disk Block Size: 64𝐾𝐵
 Memory Size: 3 × |𝑉(𝐺)| × 4𝐵 + 64 𝐾𝐵
115

116. |V| |E| Average
Degree
cit-patent 3,774,768 16,518,947 4.70
go-uniprot 6,967,956 34,770,235 4.99
citeseerx 6,540,399 15,011,259 2.30
WEBSPAM-
UK2002
105,896,555 3,738,733,568 35.00
Four Real Data Sets
116

117. Parameter Range Default
Node Size 30M - 70M 30M
Average Degree 3 - 7 5
Size of Massive SCCs 200K – 600K 400K
Size of Large SCCs 4K - 12K 8K
Size of Small SCCs 20 - 60 40
# of Massive SCCs 1 1
# of Large SCCs 30 - 70 50
# of Small SCCs 6K – 14K 10K
Synthetic Data Sets
 We construct a graph G by (1) randomly selecting all
nodes in SCCs first, (2) adding edges among the
nodes in an SCC until all nodes form an SCC, and (3)
randomly adding nodes/edges to the graph.
117

118. 1PB-SCC 1P-SCC 2P-SCC DFS-SCC
cit-patent(s) 24s 22s 701s 840s
go-uniprot(s) 22s 21s 301s 856s
citeseerx(s) 10s 8s 517s 669s
cit-patent(I/O) 16,031 13,331 133,467 667,530
go-uniprot(I/O) 26,034 47,947 471,540 619,969
citeseerx(I/O) 15,472 13,482 104,611 392,659
Performance Studies
118

119. WEBSPAM-UK2007: Vary Node Size
119

120. WEBSPAM-UK2007: Vary Memory
120

121. Synthetic Data Sets: Vary SCC Sizes
121

122. Synthetic Data Sets: Vary # of SCCs
122

123. From Semi-External to External
 Existing semi-external solutions work under the condition
that it can held a tree in main-memory 𝑘∙ |𝑉| ≤ |𝑀|, and
generate a large I/Os.
 We study an external algorithm by removing the
condition of 𝑘 ∙ |𝑉| ≤ |𝑀|.
123
A joint work by Zhiwei Zhang, Qin Lu, and Jeffrey Yu

124. The New Approach: The Main Idea
 DFS based approaches generate random accesses
 Contraction based semi-external approach
reduces |𝑉| and |𝐸| together at the same time.
 Cannot find all SCCs.
 The main idea of our external algorithm:
 Work on a small graph 𝐺’ of 𝐺 by reducing 𝑉 because 𝑀
can be small.
 Find all SCCs in 𝐺’.
 Add removed nodes back to find SCCs in 𝐺.
124

125. The New Approach: The Property
 Reducing the given graph
 𝐺 𝑉, 𝐸 → 𝐺′
𝑉′
, 𝐸′
, 𝑉 < |𝑉′
|.
 If 𝑢 can reach 𝑣 in 𝐺, 𝑢 can also reach 𝑣 in 𝐺′.
 Maintaining this property may generate a large
number of random I/O access.
 Reason: several nodes on the path from 𝑢 to 𝑣 may
be removed from 𝐺 in the previous iterations.
125

126. The New Approach: The Approach
 We introduce a new Contraction & Expansion approach.
 Contraction phase:
 Reduce nodes iteratively, 𝐺1, 𝐺2 … 𝐺𝑙.
 It decreases |𝑉(𝐺𝑖)|, but may increase |𝐸(𝐺𝑖)|.
 Expansion phase:
 In the reverse order in contraction phase,
𝐺𝑙, 𝐺𝑙−1 … 𝐺1.
 Find all SCCs in 𝐺𝑙 using a semi-external
algorithm.
 The semi-external algorithm deals with edges.
 Expand 𝐺𝑖 back to 𝐺𝑖−1.
126

127. The Contraction
 In Contraction phase, graph 𝐺1, 𝐺2 … 𝐺𝑙 are generated,
 𝐺𝑖+1 is generated by removing a batch of nodes from 𝐺𝑖.
 Stops until 𝑘 ∙ |𝑉| < |𝑀| when semi-external approach
can be applied.
G1 G2 G3
127

128. The Expansion
 In Expansion phase, removed nodes are added
 Addition is in the reverse order of their removal in
contraction phase.
G1 G2 G3
128

129. The Contraction Phase
 Compared with 𝐺𝑖, 𝐺𝑖+1should have the following
properties
 Contractable:
 |𝑉(𝐺𝑖+1)| < |𝑉(𝐺𝑖)|
 SCC-Preservable:
 𝑆𝐶𝐶(𝑢, 𝐺𝑖) = 𝑆𝐶𝐶(𝑣, 𝐺𝑖) ⟺ 𝑆𝐶𝐶(𝑢, 𝐺𝑖+1) = 𝑆𝐶𝐶(𝑣, 𝐺𝑖+1)
 Recoverable:
 𝑣 ∈ 𝑉𝑖 − 𝑉𝑖+1 ⟺ 𝑛𝑒𝑖𝑔ℎ𝑏𝑜𝑢𝑟 𝑣, 𝐺𝑖 ⊆ 𝐺𝑖+1
129

130. Contract Vi+1
 Recoverable:
 𝑣 ∈ 𝑉𝑖 − 𝑉𝑖+1 ⟺ 𝑛𝑒𝑖𝑔ℎ𝑏𝑜𝑢𝑟(𝑣, 𝐺𝑖) ⊆ 𝐺𝑖+1
 𝐺𝑖+1 is recoverable if and only if 𝑉𝑖+1 is a vertex cover of
𝐺𝑖.
 At this condition, we can determine which SCCs the
nodes in 𝐺𝑖 belong to by scanning 𝐺𝑖 once.
 For each edge, we select the node with a higher degree
or a higher order.
130

131. Contract Vi+1
c
d
h
a
b
e
f
g
i
ID1 ID2 Deg1 Deg2
a b 3 3
a d 3 4
b c 3 2
c d 2 4
d e 4 4
d g 4 4
e b 4 3
e g 4 4
f g 2 4
g h 4 2
h i 2 2
i f 2 2
DISK
For each edge, we select the node with
a higher degree or a higher order.
131

132. Construct Ei+1
 SCC-Preservable:
 𝑆𝐶𝐶(𝑢, 𝐺𝑖) = 𝑆𝐶𝐶(𝑣, 𝐺𝑖) ⟺ 𝑆𝐶𝐶(𝑢, 𝐺𝑖+1) = 𝑆𝐶𝐶(𝑣, 𝐺𝑖+1)
 If 𝑣 ∈ 𝑉𝑖 – 𝑉𝑖+1, remove (𝑣𝑖𝑛, 𝑣) and (𝑣, 𝑣 𝑜𝑢𝑡) and add (𝑣𝑖𝑛, 𝑣 𝑜𝑢𝑡).
 Although |𝐸| may be larger, |𝑉| is sure to be smaller.
 Smaller |𝑉| implies semi-external approach can be applied.
132

133. ID1 ID2
e d
b d
i g
g i
Construct Ei+1
c
d
h
a
b
e
f
g
i
ID1 ID2
d e
d g
e b
e g
DISK
If 𝑣 ∈ 𝑉𝑖 – 𝑉𝑖+1, remove (𝑣, 𝑣𝑖𝑛) and
(𝑣, 𝑣 𝑜𝑢𝑡) and add (𝑣𝑖𝑛, 𝑣 𝑜𝑢𝑡)
Existing Edges
New Edges
133

134. The Expansion Phase
 𝑆𝐶𝐶(𝑢, 𝐺𝑖) = 𝑆𝐶𝐶(𝑣, 𝐺𝑖) = 𝑆𝐶𝐶(𝑤, 𝐺𝑖) (𝑢, 𝑤 ∈ 𝑉𝑖+1)
⟺ 𝑢 → 𝑣 & 𝑣 → 𝑤 in 𝐺𝑖
 For any node 𝑣 ∈ 𝑉𝑖+1 − 𝑉𝑖, 𝑆𝐶𝐶(𝑣, 𝐺𝑖) can be
computed using
𝑛𝑒𝑖𝑔ℎ𝑏𝑜𝑢𝑟𝑖𝑛 (𝑣, 𝐺𝑖) and 𝑛𝑒𝑖𝑔ℎ𝑏𝑜𝑢𝑟𝑜𝑢𝑡(𝑣, 𝐺𝑖) only.
a
b
c
134

135. ID1 ID2
a b
a d
b c
c d
d e
d g
e b
e g
f g
g h
h i
i f
Expansion Phase
c
d
h
a
b
e
f
g
i
DISK
𝑆𝐶𝐶 𝑢, 𝐺𝑖 = 𝑆𝐶𝐶 𝑣, 𝐺𝑖 = 𝑆𝐶𝐶 𝑤, 𝐺𝑖
(𝑢, 𝑤 ∈ 𝑉𝑖+1) ⟺ 𝑢 → 𝑣 & 𝑣 → 𝑤 in 𝐺𝑖
135

136. Performance Studies
 Implement using visual C++ 2005
 Test on a PC with Intel Core2 Quard 2.66GHz CPU and 3.5GB
memory running Windows XP
 Disk Block Size: 64KB
 Default memory Size: 400𝑀
136

137. Data Set
 Real Data set
 Synthetic Data
V E Average
Degree
WEBSPAM-
UK2007
105,896,555 3,738,733,568 35.00
Parameter
Node Size 25M – 100M
Average Degree 2 - 6
Size of SCCs 20 – 600K
Number of SCCs 1 – 14 K
137

138. Performance Studies
Vary Memory Size
138

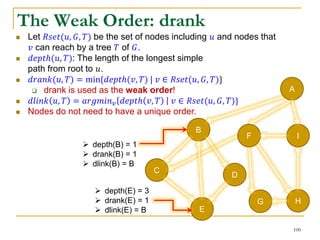
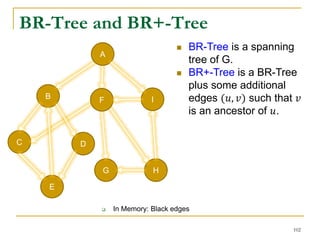
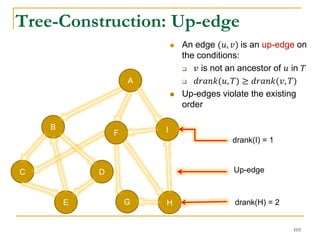
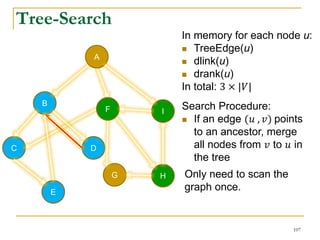
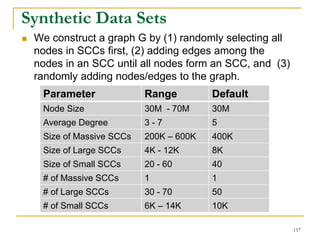
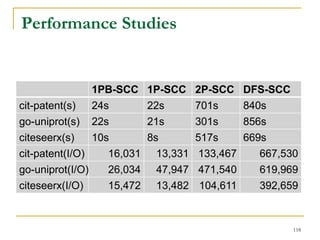
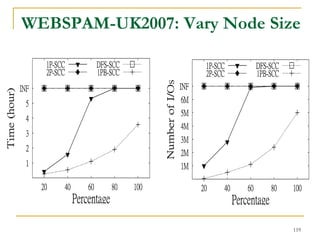
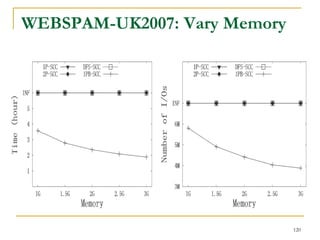
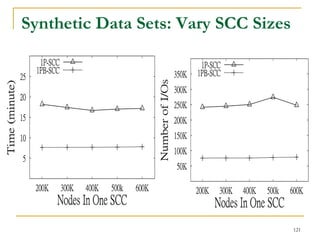
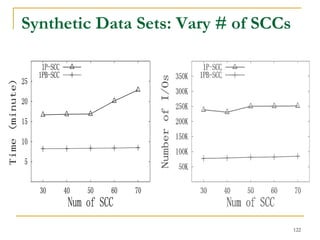
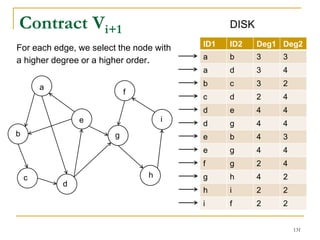
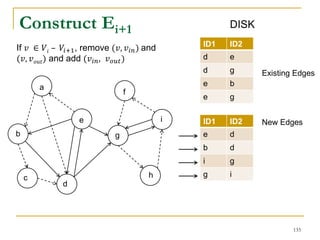
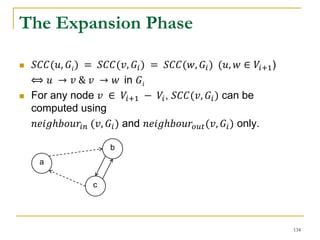
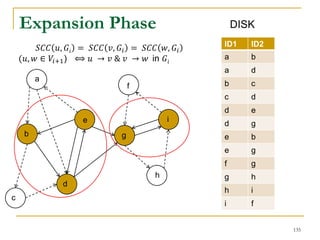
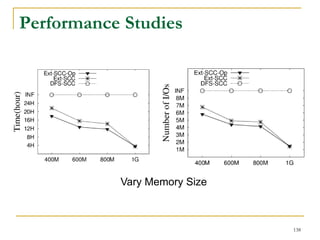
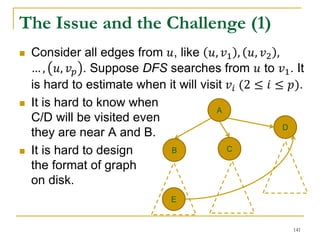
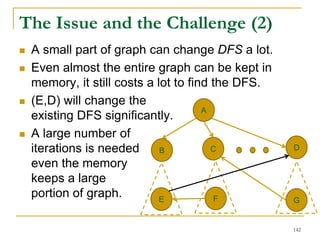
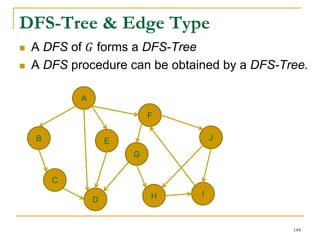
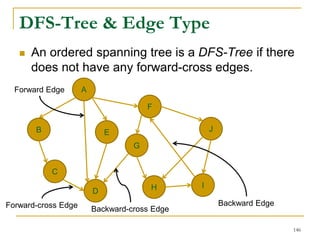
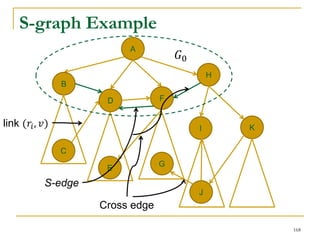
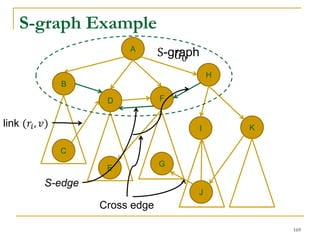
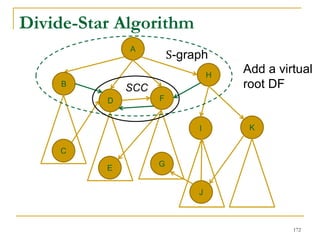
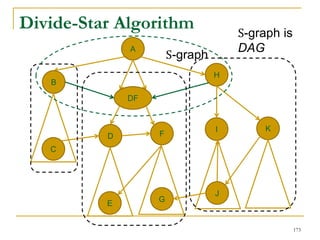
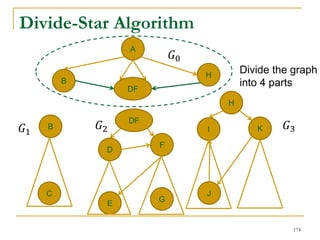
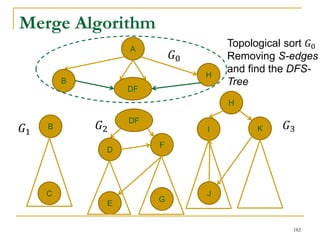
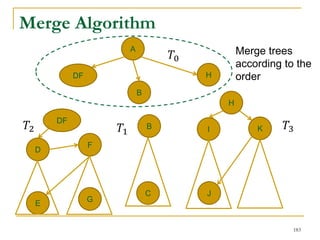
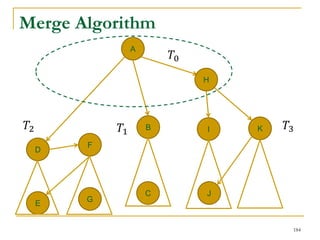
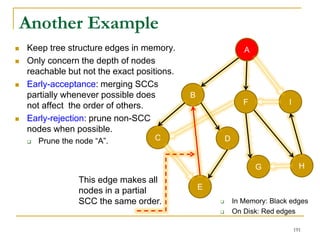
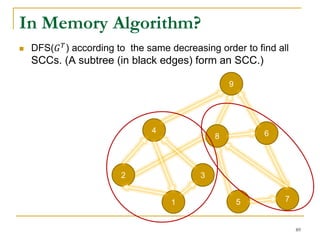
139. DFS [SIGMOD’15]
 Given a graph 𝐺(𝑉, 𝐸), depth-first search is to
search 𝐺 following the depth-first order.
A
B E
D
C
F
IH
J
G
A joint work by Zhiwei Zhang, Jeffrey Yu, Qin Lu, and Zechao Shang
139

140. The Challenge
 It needs to DFS a
massive directed graph
𝐺, but it is possible that
𝐺 cannot be entirely
held in main memory.
 Our work only keeps
nodes in memory,
which is much smaller.
140

141. The Issue and the Challenge (1)
 Consider all edges from 𝑢, like 𝑢, 𝑣1 , 𝑢, 𝑣2 ,
… , 𝑢, 𝑣 𝑝 . Suppose DFS searches from 𝑢 to 𝑣1. It
is hard to estimate when it will visit 𝑣𝑖 (2 ≤ 𝑖 ≤ 𝑝).
 It is hard to know when
C/D will be visited even
they are near A and B.
 It is hard to design
the format of graph
on disk.
A
B C
D
E
141

142. The Issue and the Challenge (2)
 A small part of graph can change DFS a lot.
 Even almost the entire graph can be kept in
memory, it still costs a lot to find the DFS.
 (E,D) will change the
existing DFS significantly.
 A large number of
iterations is needed
even the memory
keeps a large
portion of graph.
A
B C D
E F G
142

143. Problem Statement
 We study a semi-external algorithm that
computes a DFS-Tree by which DFS can be
obtained.
 The limited memory 𝑘 𝑉 ≤ 𝑀 ≤ |𝐺|
 𝑘 is a small constant number.
 𝐺 = 𝑉 + |𝐸|
143

144. DFS-Tree & Edge Type
 A DFS of 𝐺 forms a DFS-Tree
 A DFS procedure can be obtained by a DFS-Tree.
A
B E
D
C
F
IH
J
G
144

145. DFS-Tree & Edge Type
 Given a spanning tree 𝑇, there exist 4 types of
non-tree edges.
A
B E
D
C
F
IH
J
G
Forward Edge
Forward-cross Edge Backward-cross Edge
Backward Edge
145

146. DFS-Tree & Edge Type
 An ordered spanning tree is a DFS-Tree if there
does not have any forward-cross edges.
A
B E
D
C
F
IH
J
G
Forward Edge
Forward-cross Edge Backward-cross Edge
Backward Edge
146

147. Existing Solutions
 Iteratively remove the forward-cross edges.
 Procedure:
 If there exists a forward-cross edge
 Construct a new 𝑇 by conducting DFS over the
graph in memory
147

148. Existing Solutions
 Construct a new 𝑇 by conducting DFS over the graph in
memory until no forward-cross edges exist.
A
B E
D
C
F
IH
J
G
Forward-cross Edge
148

149. The Drawbacks
 D-1: A total order in 𝑉(𝐺) needs to be
maintained in the whole process.
 D-2: A large number of I/Os is produced
 Need to scan all edges in every iteration.
 D-3: A large number of iterations is needed.
 The possibility of grouping the edges near each
other in DFS is not considered.
149

150. Why Divide & Conquer
 We aim at dividing the graph into several
subgraphs 𝐺1, 𝐺2 , … , 𝐺 𝑝 with possible overlaps
among them.
 Goal: The DFS-Tree for 𝐺 can be computed by
the DFS-Trees for all 𝐺𝑖.
 Divide & Conquer approach can overcome the
existing drawbacks.
150

151. Why Divide & Conquer
 To address D-1
 A total order in 𝑉(𝐺) needs to be maintained in
the whole process.
 After dividing the graph 𝐺 into 𝐺0 , 𝐺1 , … , 𝐺 𝑝, we
only need to maintain the total order in 𝑉(𝐺𝑖).
151

152. Why Divide & Conquer
 To address D-2
 A large number of I/Os is produced.
 It needs to scan all edges in each iterations.
 After dividing the graph 𝐺 into 𝐺0 , 𝐺1 , … , 𝐺 𝑝, we
only need to scan the edges in 𝐺𝑖 to eliminate
forward-cross edges.
152

153. Why Divide & Conquer
 To address D-3
 A large number of iterations is needed.
 It cannot group the edges together that are near
each other in DFS visiting sequence.
 After dividing the graph 𝐺 into 𝐺0 , 𝐺1 , … , 𝐺 𝑝, the
DFS procedure can be applied to 𝐺𝑖 independently.
153

154. Valid Division
A
B
F
C
D
E
𝐺1
𝐺2
A
B
F
C
D
E
𝐺1
𝐺2
The left is not a DFS-tree The right is a DFS-tree
154

155. Invalid Division
 An example:
A
B
F
C
D
E
𝐺1
𝐺2
No matter how the DFS-
Trees for 𝐺1 and 𝐺2 are
ordered, the merged tree
cannot be a DFS-Tree for 𝐺.
155

156. How to Cut: Challenges
 Challenge-1: uneasy to check whether a division
is valid.
 Need to make sure a DFS-Tree for a divided subgraph
will not affect the DFS-Tree of others.
 Challenge-2: finding a good division is non-trivial.
 The edge types between different subgraphs are
complicated.
 Challenge-3: The merge procedure needs to
make sure that the result is the DFS-Tree for 𝐺.
156

157. Our New Approach
 To address Challenge-1:
 Compute a light-weight summary graph (S-graph)
denoted as 𝐺.
 Check whether a division is valid by searching 𝐺
 To address Challenge-2:
 Recursively divide & conquer.
 To address Challenge-3:
 The DFS-Tree for 𝐺 is computed only by 𝑇𝑖 and 𝐺.
157

158. Four Division Properties
 Node-Coverage: 1 ≤ 𝑖 ≤ 𝑝 𝑉 𝐺𝑖 = 𝐺
 Contractible: 𝑉 𝐺𝑖 < |V(𝐺)|
 Independence: any pair of nodes in
𝑉 𝑇𝑖 ∩ 𝑉(𝑇𝑗) are consistent.
 𝑇𝑖 and 𝑇𝑗 can be dealt with independently
(𝑇𝑖 and 𝑇𝑗 are DFS-Tree for 𝐺𝑖 and 𝐺𝑗)
 DFS-Preservable: there exists a DFS-Tree 𝑇 for
graph 𝐺 such that 𝑉 𝑇 = 1≤𝑖≤𝑝 𝑉(𝑇𝑖) and
E 𝑇 = 1≤𝑖≤𝑝 𝐸(𝑇𝑖)
 DFS-Tree for 𝐺 can be computed by 𝑇𝑖
158

159. DFS-Preservable Property
 DFS-Tree for 𝐺 can be computed by 𝑇𝑖.
 DFS∗
-Tree: A spanning tree with the same edge
set of a DFS-Tree (without order).
 Suppose the independence property is satisfied,
then the DFS-preservable property is satisfied if
and only if the spanning tree T with 𝑉 𝑇 =
1≤𝑖≤𝑝 𝑉(𝑇𝑖) and 𝐸 𝑇 = 1≤𝑖≤𝑝 𝐸(𝑇𝑖) is a 𝐷𝐹𝑆∗-
Tree.
159

160. Independence Property
 Any pair of nodes in 𝑉 𝑇𝑖 ∩ 𝑉(𝑇𝑗) are consistent
(𝑇𝑖 and 𝑇𝑗 are DFS-Tree for 𝐺𝑖 and 𝐺𝑗).
 𝑇𝑖 , 𝑇𝑗 can be dealt with independently.
 This may not hold: 𝑢 is an ancestor of 𝑣 in 𝑇𝑖, but
is a sibling in 𝑇𝑗.
 Theorem:
 Given a division 𝐺0, 𝐺1, … , 𝐺 𝑝 of 𝐺, the
independence property is satisfied if and only if for
any subgraphs 𝐺𝑖 and 𝐺𝑗, 𝐸 𝐺𝑖 ∩ 𝐸 𝐺𝑗 = ∅.
160

161. Independence Property
C
A
ED
B
F
𝐺1
𝐺3
𝐺2
161

162. DFS-Preservable Example
A
B
D
C
E
F
G
 DFS-preservable
property is not satisfied.
 The DFS-Tree for 𝐺 does
not exist given the DFS-
Tree for each subgraph.
 Forward-cross edges
always exist.
162

163. Our Approach
 Root based division: independence is satisfied.
 For each 𝐺𝑖, it has a spanning tree 𝑇𝑖.
 For a division 𝐺0, 𝐺1, …, 𝐺 𝑝, 𝐺0 ∩ 𝐺𝑖 = 𝑟𝑖.
 𝑟𝑖 is the root of 𝑇𝑖 and the leaf of 𝑇0
𝐺0
𝐺𝑖 𝐺𝑗
163

164. Our Approach
 We expand 𝐺0 to capture the relationship between
different 𝐺𝑖 and call it S-graph.
 S-graph is used to check whether the current division
is valid (DFS-preservable property is satisfied)
𝐺0
𝐺𝑖 𝐺𝑗
S-graph
164

165. S-edge
 S-edge: given a spanning tree 𝑇 of 𝐺, (𝑢′
, 𝑣′
) is the
S-edge of 𝑢, 𝑣 if
 𝑢′ is ancestor of 𝑢 and 𝑣′ is ancestor of 𝑣 in 𝑇,
 Both 𝑢′, 𝑣′ are the children of 𝐿𝐶𝐴(𝑢, 𝑣), where
𝐿𝐶𝐴(𝑢, 𝑣) is the lowest common ancestor of 𝑢, 𝑣 in 𝑇.
165

166. S-edge Example
A
B
D
H
I
E
K
F
C
J
𝐺0
Cross edge
S-edge
G
166

167. S-graph
 For a division 𝐺0, 𝐺1, …, 𝐺 𝑝 and 𝑇0 is the DFS-Tree
for 𝐺0, S-graph 𝐺 is constructed in the following:
 Remove all backward and forward edges w.r.t. 𝑇0
 Replace all cross-edges (𝑢, 𝑣) with their
corresponding S-edge if the S-edge is between nodes
in 𝐺0,
 For edge (𝑢, 𝑣), if 𝑢 ∈ 𝐺𝑖 and 𝑣 ∈ 𝐺0, add edge (𝑟𝑖, 𝑣)
and do the same for 𝑣.
167

168. S-graph Example
A
B
D
H
I
E
K
F
C
J
𝐺0
Cross edge
S-edge
G
link (𝑟𝑖, 𝑣)
168

169. S-graph Example
A
B
D
H
I
E
K
F
C
J
𝐺0
Cross edge
S-edge
G
link (𝑟𝑖, 𝑣)
S-graph
169

170. Division Theorem
 Consider a division 𝐺0, 𝐺1, …, 𝐺 𝑝 and suppose 𝑇0 is
the DFS-Tree for 𝐺0, the division is DFS-preservable
if and only if the S-graph 𝐺 is a DAG.
170

171. Divide-Star Algorithm
 Divide 𝐺 according to the children of the root 𝑅 of 𝐺.
 If the corresponding S-graph 𝐺 is a DAG, each
subgraph can be computed independently.
 Deal with strongly connected component:
 Modify 𝑇: add a virtual node RS representing a SCC S.
 Modify 𝐺:
 For any edge (𝑢, 𝑣) in S-graph 𝐺, if 𝑢 ∉ 𝑆 and 𝑣 ∈ 𝑆,
add edge (𝑢, 𝑅𝑆). Do the same for 𝑣.
 Remove all nodes in S and corresponding edges.
 Modify Division: create a new tree 𝑇′ rooted at the
virtual root RS and connect to the roots in the SCC.
171

172. Divide-Star Algorithm
A
B
D
H
I
E
K
F
C
J
G
S-graph
SCC
Add a virtual
root DF
172

173. Divide-Star Algorithm
A
B
D
H
I
E
K
F
C
J
G
S-graph
DF
S-graph is
DAG
173

174. Divide-Star Algorithm
A
B
D
H
I
E
K
F
J
G
𝐺0
DF
Divide the graph
into 4 parts
B
C
DF
H
𝐺1
𝐺2 𝐺3
174

175. Divide-TD Algorithm
 Divide-Star algorithm divides the graph according to
the children of the root.
 The depth of 𝑇0 is 1.
 The max number of subgraphs after dividing will not
be larger than the number of children.
 Divide-TD algorithm enlarges 𝑇0 and the
corresponding S-graph.
 It can result in more subgraphs than that Divide-Star
can provide.
175

176. Divide-TD Algorithm
 Divide-TD algorithm enlarges 𝑇0 to a Cut-Tree.
 Cut-Tree: Given a tree 𝑇 with root 𝑡0, a cut-tree 𝑇𝑐 is
a subtree of 𝑇 which satisfies two conditions.
 The root of 𝑇𝑐 is 𝑡0.
 For any node 𝑣 ∈ 𝑇 with child nodes 𝑣1, 𝑣2, … , 𝑣 𝑘, if 𝑣 ∈
𝑇𝑐, then either 𝑣 is a leaf node or a node in 𝑇𝑐 with all
child nodes 𝑣1, 𝑣2, … , 𝑣 𝑘.
 With such conditions, for any S-edge (𝑢, 𝑣), only two
situations exist.
 𝑢, 𝑣 ∈ 𝑇𝑐
 𝑢, 𝑣 ∉ 𝑇𝑐
176

177. Cut-Tree Construction
 Given a tree T with root 𝑟0.
 Initially 𝑇𝑐 contains only the root 𝑟0.
 Iteratively pick a leaf node 𝑣 in 𝑇𝑐 and all the child nodes
of 𝑣 in 𝑇.
 The process stops until the memory cannot hold it after
adding the next nodes.
177

178. Divide-TD Algorithm
A
B
D
H
I
E
K
F
C
J
G
Cut-Tree 𝑇𝑐
178

179. Divide-TD Algorithm
A
B
D
H
I
E
K
F
C
J
G
Add a virtual
node DF
SCC
Cut-Tree 𝑇𝑐
179

180. Divide-TD Algorithm
A
B
D
I
E
K
F
J
G
DF
S-Graph is a DAG
Divide the graph
into 5 parts
B
C
DF
H
𝐺1
𝐺2 𝐺3 I K𝐺4
𝐺0
180

181. Merge Algorithm
 According to the properties, the DFS-Tree for
subgraphs are 𝑇0 , 𝑇1 ,…,𝑇𝑝, there exists a DFS-Tree T
with 𝑉 𝑇 = 1≤𝑖≤𝑝 𝑉(𝑇𝑖) and 𝐸 𝑇 = 1≤𝑖≤𝑝 𝐸(𝑇𝑖).
 Only need to organize 𝑇𝑖 in the merged tree such that
the result tree 𝑇 is a DFS-Tree.
 Since S-graph 𝐺 is a DAG in the division procedure,
we can topological sort 𝐺 and organize 𝑇𝑖 according to
the topological order.
 Remove virtual nodes 𝑣 and add edges from the father
of 𝑣 to the children of 𝑣.
 It can be proven that the result tree is a DFS-Tree.
181

182. Merge Algorithm
A
B
D
H
I
E
K
F
J
G
𝐺0
DF
B
C
DF
H
𝐺1
𝐺2 𝐺3
Topological sort 𝐺0
Removing S-edges
and find the DFS-
Tree
182

183. Merge Algorithm
A
B
D
H
I
E
K
F
J
G
𝑇0
DF
B
C
DF
H
𝑇1
𝑇2 𝑇3
Merge trees
according to the
order
183

184. Merge Algorithm
A
B
D
I
E
K
F
J
G
𝑇0
C
H
𝑇1
𝑇2 𝑇3
184

185. Performance Studies
 Implement using visual C++ 2010
 Test on a PC with Intel Core2 Quard 2.66GHz
CPU and 4GB memory running Windows 7
Enterprise
 Disk Block Size: 64KB
185

186. |V| |E| Average
Degree
Wikilinks 25,942,246 601,038,301 23.16
Arabic-2005 22,744,080 639,999,458 28.14
Twitter-2010 41,652,230 1,468,365,182 35.25
WEBGRAPH-
UK2007
105,895,908 3,738,733,568 35.00
Four Real Data Sets
186

187. Web-graph Results
 Memory size 2GB
 Varying node size percentage
187

188.  We study the I/O efficient DFS algorithms for a large
graph.
 We analyze the drawbacks of existing semi-external
DFS algorithm.
 We discuss the challenges and four properties in
order to find a divide & conquer approach.
 Based on the properties, we design two novel graph
division algorithms and a merge algorithm to reduce
the cost to DFS the graph.
 We have conducted extensive performance studies to
confirm the efficiency of our algorithms.
Conclusion
188

189.  We also believe that there are many things we need
to do on large graphs or big graphs.
 We know what we have known on graph processing.
 We do not know yet what we do not know on graph
processing.
 We need to explore many directions such as
 parallel computing
 distributed computing
 streaming computing
 semi-external/external computing.
Some Conclusion Remarks
189

190. I/O Cost Minimization
 If there does not exist node 𝑢 for 𝑣 that 𝑆𝐶𝐶(𝑢, 𝐺𝑖) =
𝑆𝐶𝐶(𝑣, 𝐺𝑖), 𝑣 can be removed from 𝐺𝑖+1.
 For a node 𝑣, if 𝑛eigh𝑏𝑜𝑢𝑟(𝑣, 𝐺𝑖) ⊆ 𝑉𝑖+1, 𝑣 can be
removed from 𝑉𝑖+1.
 The I/O complexity is
𝑂(𝑠𝑜𝑟𝑡 𝑉𝑖 + 𝑠𝑜𝑟𝑡 𝐸𝑖 + 𝑠𝑐𝑎𝑛(|𝐸𝑖|))
190

191. B
H
C D
G
E
A
IF
This edge makes all
nodes in a partial
SCC the same order.
Another Example
 Keep tree structure edges in memory.
 Only concern the depth of nodes
reachable but not the exact positions.
 Early-acceptance: merging SCCs
partially whenever possible does
not affect the order of others.
 Early-rejection: prune non-SCC
nodes when possible.
 Prune the node “A”.
 In Memory: Black edges
 On Disk: Red edges
191

192. B
I
C
D
H
E
A
JG
 No need to remember
𝑑𝑙𝑖𝑛𝑘(𝑢, 𝑇).
 Merge nodes of the
same order when an
edge (𝑢, 𝑣) is found,
where 𝑣 is an
ancestor of 𝑢 in 𝑇.
 Smaller graph size,
smaller I/O Cost
KF
Up-edge: Modify Tree
Up-edge: Modify Tree
Memory: 2 × |𝑉|
Early-Acceptance
Early-Acceptance
Optimization: Early Acceptance
192

193. Performance Studies
Vary Degree
193