Recommended
PPTX
PPTX
PDF
10分で分かるr言語入門ver2.10 14 1101
PDF
10分で分かるr言語入門ver2 upload用
PPTX
PPTX
PPTX
PDF
PDF
10分で分かるr言語入門ver2.14 15 0905
PDF
10分で分かるr言語入門ver2.15 15 1010
PDF
R入門(dplyrでデータ加工)-TokyoR42
PPTX
PDF
PPTX
PDF
10分で分かるr言語入門ver2.9 14 0920
PDF
PDF
PDF
Tokyor60 r data_science_part1
PDF
PDF
2017年3月版データマエショリスト入門(誤植修正版)
PDF
PDF
PDF
PDF
PDF
PPTX
20161127 doradora09 japanr2016_lt
PDF
PDF
PPTX
PPTX
More Related Content
PPTX
PPTX
PDF
10分で分かるr言語入門ver2.10 14 1101
PDF
10分で分かるr言語入門ver2 upload用
PPTX
PPTX
PPTX
PDF
What's hot
PDF
10分で分かるr言語入門ver2.14 15 0905
PDF
10分で分かるr言語入門ver2.15 15 1010
PDF
R入門(dplyrでデータ加工)-TokyoR42
PPTX
PDF
PPTX
PDF
10分で分かるr言語入門ver2.9 14 0920
PDF
PDF
PDF
Tokyor60 r data_science_part1
PDF
PDF
2017年3月版データマエショリスト入門(誤植修正版)
PDF
PDF
PDF
PDF
PDF
PPTX
20161127 doradora09 japanr2016_lt
PDF
PDF
Viewers also liked
PPTX
PPTX
PDF
PDF
東京R非公式おじさんが教える本当に気持ちいいパッケージ作成法
PDF
PDF
PDF
RとJavaScript Visualizationを俯瞰しよう
ODP
PDF
R言語で始めよう、データサイエンス(ハンズオン勉強会) 〜機会学習・データビジュアライゼーション事始め〜
PDF
[データマイニング+WEB勉強会][R勉強会] R言語によるクラスター分析 - 活用編
PDF
[データマイニング+WEB勉強会][R勉強会] はじめてでもわかる R言語によるクラスター分析 - 似ているものをグループ化する-
PDF
PDF
20170923 excelユーザーのためのr入門
PDF
PDF
RとStanでクラウドセットアップ時間を分析してみたら #TokyoR
PDF
PPT
PDF
20140625 rでのデータ分析(仮) for_tokyor
PDF
PPTX
Similar to Tokyo r33 beginner
PPTX
PDF
R language definition3.1_3.2
PDF
PPT
12-11-30 Kashiwa.R #5 初めてのR Rを始める前に知っておきたい10のこと
PPT
PDF
PDF
PPT
PDF
PDF
PDF
PPTX
PDF
PPTX
PPTX
PDF
PDF
PDF
PDF
DOCX
More from Takashi Minoda
PDF
PPTX
RStudioでRをはじめよう(R for Beginner using RStudio)
PPTX
RからGoogle Cloud Vision API を利用する
PPTX
PPTX
PPTX
PPTX
PPTX
Tokyo r24 r_graph_tutorial
PPTX
PDF
PDF
PDF
ODP
PPT
ODP
PDF
Tokyo r33 beginner 1. 2. 3. • 名前 :簑田 高志
• Twitter :aad34210
• ブログ :http://pracmper.blogspot.com/
• 出身地 :熊本県
• 出身学部 :法学部
• 仕事 :インターネット広告のビジネスアナリ
スト
自己紹介
4. 5. 6. 7. 8. 9. 10. 11. 12. 条件分岐
• SWITCH文
• 複数の条件で分岐させたい場合
• switch(データ,ケース1 , ケース2 , 一致する場合がないケース)
• 例えば…
• Tokyoから売上が上がっている場合は、Japanを。それ以外はOther
city <- "Tokyo”
switch(city ,"Tokyo" = print("Japan") , print("Other"))
13. 14. 15. FOR文
• For文
• ある処理を繰り返し行いたい場合に利用する。
• for (ループ変数 in リスト) {処理}
• 例えば…
• 1〜5までを合計する。
• ベクトルを表示させる。
x <- 0
for (i in 1:5) {x <- x +1}
x
x <- c(10000 , 20000 , 30000)
for (i in 1:length(x)){print(x[i])}
16. 17. 18. 例題(2)
• 前のページの問題は意外とすぐにとける
• 問題
• 1〜100までの数字の中で、
• 3の倍数 :“Aho” と表示
• 5 の倍数 :“アホ” と表示
• 回答
• For文で1:100までをベクトル生成
• 3の倍数:“%%”で余りを計算し割り切れる数を判定
• 5の倍数:“%%”で余りを計算し割り切れる数を判定
• それぞれIF文で“Aho”か“アホ”か判定
• Print文で表示
• では、世界のナベアツでやってみよう。
19. 例題(3)
for( i in 1:100) {
if (i%%3 == 0 ) {print("Aho")}
else if (i%%5 == 0) {print("アホ")}
else {print(i)}
}
nabeatsu <- function(n , baisuu1 , baisuu2) {
for( i in 1:n) {
if (i%%baisuu1 == 0 ) {print("Aho")}
else if (i%%baisuu2 == 0) {print("アホ")}
else {print(i)}
}
}
関数化(Function)にしてみよう。
利用する変数
・ベクトル数 :n
・Ahoと表示する倍数 :baisuu1
・アホと表示する倍数 :baisuu2
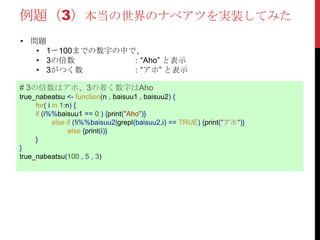
20. 21. 例題(3)本当の世界のナベアツを実装してみた
# 3の倍数はアホ、3の着く数字はAho
true_nabeatsu <- function(n , baisuu1 , baisuu2) {
for( i in 1:n) {
if (i%%baisuu1 == 0 ) {print("Aho")}
else if (!i%%baisuu2|grepl(baisuu2,i) == TRUE) {print("アホ")}
else {print(i)}
}
}
true_nabeatsu(100 , 5 , 3)
• 問題
• 1〜100までの数字の中で、
• 3の倍数 :“Aho” と表示
• 3がつく数 :“アホ” と表示
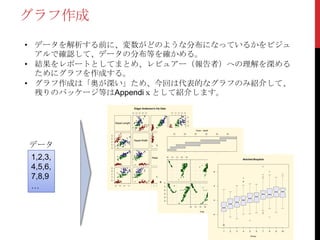
22. 23. グラフ作成
• データを解析する前に、変数がどのような分布になっているかをビジュ
アルで確認して、データの分布等を確かめる。
• 結果をレポートとしてまとめ、レビュアー(報告者)への理解を深める
ためにグラフを作成する。
• グラフ作成は「奥が深い」ため、今回は代表的なグラフのみ紹介して、
残りのパッケージ等はAppendixとして紹介します。
1,2,3,
4,5,6,
7,8,9
…
データ
Sepal.Length
2.0 2.5 3.0 3.5 4.0 0.5 1.0 1.5 2.0 2.5
4.55.56.57.5
2.02.53.03.54.0
Sepal.Width
Petal.Length
1234567
4.5 5.5 6.5 7.5
0.51.01.52.02.5
1 2 3 4 5 6 7
Petal.Width
Edgar Anderson's Iris Data
-35-30-25-20-15-10
165 170 175 180 185
165 170 175 180 185 165 170 175 180 185
-35-30-25-20-15-10
long
lat
100 200 300 400 500 600
Given : depth
1 2 3 4 5 6 7 8 9 10
0246
Notched Boxplots
Group
24. 散布図
• データがどのような散らばり具合をしているのかを調査したい場合、散
布図を描きます。
• plot(x , y)
#ベクトルの表示
data <- c(1:100)
plot(data)
#irisのSepal.lengthとSepal.Widthの散布図
plot(iris[,1] , iris[,2])
0 20 40 60 80 100
020406080100
Index
data
#ベクトルの表示
4.5 5.0 5.5 6.0 6.5 7.0 7.5 8.0
2.02.53.03.54.0
iris[, 1]
iris[,2]
#irisのSepal.lengthと
Sepal.Widthの散布図
25. 26. Sepal.Length
2.0 2.5 3.0 3.5 4.0 0.5 1.0 1.5 2.0 2.5
4.55.56.57.5
2.02.53.03.54.0
Sepal.Width
Petal.Length
1234567
4.5 5.5 6.5 7.5
0.51.01.52.02.5
1 2 3 4 5 6 7
Petal.Width
散布図
Sepal.Length
2.0 2.5 3.0 3.5 4.0 0.5 1.0 1.5 2.0 2.5
4.55.56.57.5
2.02.53.03.54.0
Sepal.Width
Petal.Length
1234567
4.5 5.5 6.5 7.5
0.51.01.52.02.5
1 2 3 4 5 6 7
Petal.Width
#複数変数の散布図組合せ(対散布図) #複数変数の対散布図(種類による色分け)
27. 28. 29. 30. aho
01020304050
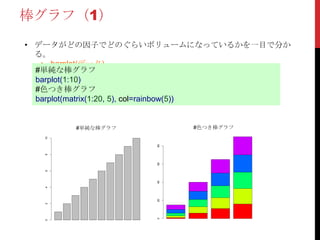
棒グラフ(3)
• 先ほどの“Aho”、“アホ”をそれぞれカウントして棒グラフを作ってみま
しょう。
#データフレームの作成
aho_data <- data.frame(1:100)
#グラフ用データの作成
aho_data$hantei <- ifelse(aho_data[,1]%%3 == 0,"aho",ifelse(aho_data[,1]%%5 == 0 ,"アホ","天才
"))
#Barplotの作成
barplot(table(aho_data[,2]) , col = c("green" , "blue" , "red"))
31. 32. 33. 34. 35. 36. 37. まとめ
• IF文
• 条件分岐をさせたい時に利用する。ifelse も使えるよ
• For文
• 繰り返し処理を行いたい場合に利用する。
• 条件が正の場合に繰り返し処理をするWhileもある。
• FizzBuzz
• IF文とFor文を使って、FizzBuzz問題を解く。
• 世界のナベアツもできるよ!
• グラフ作成
• 奥の深い世界…
• demo(graphics)で試してみよう。
• plot,barplot
• ggplot2など様々なパッケージがある。
• 統計解析
• 簡単な関数で、統計量を計算することができる。
• max,min,range,quantile,summary
38. 39.











![FOR文
• For文
• ある処理を繰り返し行いたい場合に利用する。
• for (ループ変数 in リスト) {処理}
• 例えば…
• 1〜5までを合計する。
• ベクトルを表示させる。
x <- 0
for (i in 1:5) {x <- x +1}
x
x <- c(10000 , 20000 , 30000)
for (i in 1:length(x)){print(x[i])}](https://image.slidesharecdn.com/tokyor33beginner-130831013206-phpapp01/85/Tokyo-r33-beginner-15-320.jpg)






![散布図
• データがどのような散らばり具合をしているのかを調査したい場合、散
布図を描きます。
• plot(x , y)
#ベクトルの表示
data <- c(1:100)
plot(data)
#irisのSepal.lengthとSepal.Widthの散布図
plot(iris[,1] , iris[,2])
0 20 40 60 80 100
020406080100
Index
data
#ベクトルの表示
4.5 5.0 5.5 6.0 6.5 7.0 7.5 8.0
2.02.53.03.54.0
iris[, 1]
iris[,2]
#irisのSepal.lengthと
Sepal.Widthの散布図](https://image.slidesharecdn.com/tokyor33beginner-130831013206-phpapp01/85/Tokyo-r33-beginner-24-320.jpg)
![散布図
• 変数が多くある場合、変数の1つずつの組み合わせだと手間がかかるので、
一気に組み合わせてみてみたい場合。
• plot(dataframe)
• pars(dataframe)
#複数変数の散布図組合せ(対散布図)
plot(iris[-5])
#複数変数の対散布図(種類による色分け)
pairs(iris[1:4], pch = 21,bg = c("red" , "green3" ,
"blue")[unclass(iris$Species)])](https://image.slidesharecdn.com/tokyor33beginner-130831013206-phpapp01/85/Tokyo-r33-beginner-25-320.jpg)

![線グラフ(折れ線グラフ)
• データがどのように変化しているのかを分かるようにする。
• 実は折れ線グラフは散布図にラインを引いただけなので比較的簡単に作
成できます。(type = “l”を指定)
• plot(データ , type = “l”)
#aho_dataを使って折れ線グラフ
plot(aho_data[,1] , type = "l”)
0 20 40 60 80 100
020406080100
Index
aho_data[,1]](https://image.slidesharecdn.com/tokyor33beginner-130831013206-phpapp01/85/Tokyo-r33-beginner-27-320.jpg)
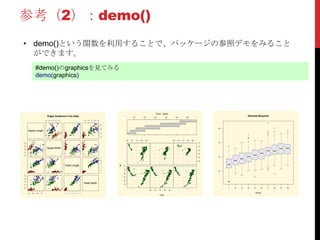
![棒グラフ(2)
• データがどの因子でどのぐらいボリュームになっているかを一目で分か
る。
• barplot(データ)
#種類ごとでの棒グラフ
barplot(table(iris[,5]))
#色を付けたい場合
barplot(table(iris[,5]),col = c("red" , "green" ,"yellow"))
#単純な棒グラフ #色つき棒グラフ
setosa versicolor virginica
01020304050
setosa versicolor virginica
01020304050](https://image.slidesharecdn.com/tokyor33beginner-130831013206-phpapp01/85/Tokyo-r33-beginner-29-320.jpg)
![aho
01020304050
棒グラフ(3)
• 先ほどの“Aho”、“アホ”をそれぞれカウントして棒グラフを作ってみま
しょう。
#データフレームの作成
aho_data <- data.frame(1:100)
#グラフ用データの作成
aho_data$hantei <- ifelse(aho_data[,1]%%3 == 0,"aho",ifelse(aho_data[,1]%%5 == 0 ,"アホ","天才
"))
#Barplotの作成
barplot(table(aho_data[,2]) , col = c("green" , "blue" , "red"))](https://image.slidesharecdn.com/tokyor33beginner-130831013206-phpapp01/85/Tokyo-r33-beginner-30-320.jpg)



![統計解析
• グラフ作成と同様に奥のふかーい分野。
• 今回はデータ全体がどのような分布になっているかを簡単に調査するための関数を紹
#最大値
max(aho_data[,1])
#最小値
min(aho_data[,1])
#レンジ(最大値、最小値)
range(aho_data[,1])
#平均
mean(aho_data[,1])
#中央値
median(aho_data[,1])
#四分位点
quantile(aho_data[,1] )
#サマリ(平均値、中央値、四分位点)
summary(aho_data[,1])
各種統計パッケージの話は、過去や今後のTokyoRで見てみてください!](https://image.slidesharecdn.com/tokyor33beginner-130831013206-phpapp01/85/Tokyo-r33-beginner-35-320.jpg)