TokyoR

1. Rによるやさしい統計学
分散分析
（後半の後半）
TOKYO.R #31
簑田 高志

2. 目次
1.自己紹介
2.前回のおさらい
3.二元配置分散分析（二要因とも対応あり）
4.二元配置分散分析（一要因のみ対応あり）
5.まとめ
※ スクリーンショットや機能等はMac版となります。
基本的にはWindowsも同じものがあるはずです。

3. 目次【前回】
1.自己紹介
2.分散分析（おさらい）
3.二元配置分散分析（対応なし）
4.二元配置分散分析（二要因とも対応あり）
5.二元配置分散分析（一要因のみ対応あり）
6.まとめ
※ スクリーンショットや機能等はMac版となります。
基本的にはWindowsも同じものがあるはずです。

4. 目次【前回】
1.自己紹介
2.分散分析（おさらい）
3.二元配置分散分析（対応なし）
4.二元配置分散分析（二要因とも対応あり）
5.二元配置分散分析（一要因のみ対応あり）
6.まとめ
※ スクリーンショットや機能等はMac版となります。
基本的にはWindowsも同じものがあるはずです。
今回はここ↓から

5. 目次
1.自己紹介
2.前回のおさらい
3.二元配置分散分析（二要因とも対応あり）
4.二元配置分散分析（一要因のみ対応あり）
5.まとめ
※ スクリーンショットや機能等はMac版となります。
基本的にはWindowsも同じものがあるはずです。

6. • 名前 :簑田 高志
• Twitter :aad34210
• ブログ :http://pracmper.blogspot.com/
• 仕事 :ビジネスアナリスト
• R歴 ：3年程度
自己紹介

7. 目次
1.自己紹介
2.前回のおさらい
3.二元配置分散分析（二要因とも対応あり）
4.二元配置分散分析（一要因のみ対応あり）
5.まとめ
※ スクリーンショットや機能等はMac版となります。
基本的にはWindowsも同じものがあるはずです。

8. 分散分析【前回】
• 分散分析
3つ以上の平均値を比較するための統計的方法
2つの平均値を比較する方法は「t検定」
テキスト160p~から
• Rにおける関数
 oneway.test
 aov
 anova

9. 二元配置分散分析（対応なし）【前回】
うちのミネラルウォーター商品って、銘柄ごとに温度が違えば、
おいしさって違うのかな。おーい、ちょっとしらべてくれー
はいはい、了解しましたっ
と。
データのフォーマットはこれでよさそうだな。
これで分析にかけてみよう。

10. 二元配置分散分析（対応なし）【前回】
• 主効果：それぞれの要因ごとの効果
 “温度の違い”（冷蔵か常温に違いがある）
• 交互作用効果：2つ以上の要因が組み合わされ
た場合に生じる効果。単純に2つの要因の足し
算ではない
 温度が冷たい場合、5点押し上げる
 ビビッテルは温度が低いと美味しくない
→ 単純な足し算ではない
主効果
交互作用効果

11. 二元配置分散分析（対応なし）【前回】
• まとめ
1.主効果と交互作用効果
2.仮説の立て方
3.aov関数
4.Interaction.plot
5.交互作用が起こっているグラフの見方

12. 交互作用があって、温度によって差がありそうだってことはわ
かった
げ・・・
でもさー、もしかして評価した人のバイアスってかかってな
い？？
そこも評価してみてよー

13. 目次（前回）
1.自己紹介
2.分散分析（おさらい）
3.二元配置分散分析（対応なし）
4.二元配置分散分析（二要因とも対応あり）
5.二元配置分散分析（一要因のみ対応あり）
6.まとめ
やるかもね
↑いまココ

14. 目次
1.自己紹介
2.前回のおさらい
3.二元配置分散分析（二要因とも対応あり）
4.二元配置分散分析（一要因のみ対応あり）
5.まとめ
※ スクリーンショットや機能等はMac版となります。
基本的にはWindowsも同じものがあるはずです。

15. 二元配置分散分析（二要因とも対応あり）
課題：自社商品は銘柄ごとに温度が変わると
美味しさがかわるのか? ヒトごとに評価をし
てもらった。
このデータを使って、温度（冷蔵庫、常温）や銘柄の違いによっ
美味しさの評定の母平均は異なるといえるか？

16. 二元配置分散分析（二要因とも対応あり）
• 実際に分析
1. 帰無仮説と対立仮説の設定
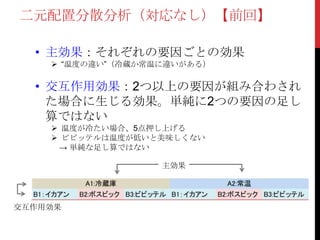
• これまでの検定と同じように1つの仮説では無く、「主効果」、「交
互作用効果の設定が必要
• 要因A（温度）の主効果
− 帰無仮説：温度が違っても美味しさの得点の母平均は等しい
− 対立仮説：温度の違いによって美味しさ得点の母平均は異なる
• 要因B（銘柄）の主効果
− 帰無仮説：銘柄が違ってもおいしさ得点の母平均は等しい
− 対立仮説：銘柄の違いによって、母平均は異なる
• 要因Aと要因Bの交互作用効果
− 帰無仮説：温度と銘柄の組み合わせに相性の良し悪しはない
− 対立仮説：温度と銘柄の組み合わせに相性の良し悪しがある
2. 有意水準
• 5%

17. 二元配置分散分析（二要因とも対応あり）
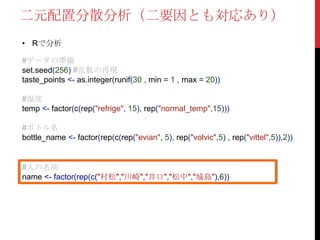
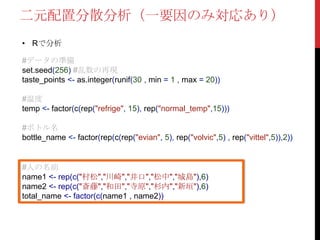
• Rで分析
#データの準備
set.seed(256) #乱数の再現
taste_points <- as.integer(runif(30 , min = 1 , max = 20))
#温度
temp <- factor(c(rep("refrige", 15), rep("normal_temp",15)))
#ボトル名
bottle_name <- factor(rep(c(rep("evian", 5), rep("volvic",5) , rep("vittel",5)),2))
#人の名前
name <- factor(rep(c("村松","川崎","井口","松中","城島"),6))

18. • Rで分析
summary(aov(taste_points~temp*bottle_name
+Error(name+name:temp+name:bottle_name+name:temp:bottle_name)))
温度、銘柄の主効果には違
いがなく、交互作用効果に
違いが見られる。
（5％水準で有意）
二元配置分散分析（二要因とも対応あり）

19. 目次
1.自己紹介
2.前回のおさらい
3.二元配置分散分析（二要因とも対応あり）
4.二元配置分散分析（一要因のみ対応あり）
5.まとめ
※ スクリーンショットや機能等はMac版となります。
基本的にはWindowsも同じものがあるはずです。

20. 二元配置分散分析（一要因のみ対応あり）
 前回のアンケートでは、一人に6本の水を評
価してもらった。
 しかし、6本の水を飲むのは大変だ！
というご意見があったため、一人3本の水を
飲んで もらうことにした。
（･ω･´#）<ﾉﾐｽｷﾞｼﾞｬ

21. 二元配置分散分析（一要因のみ対応あり）
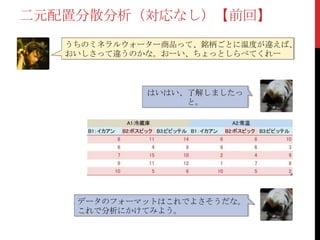
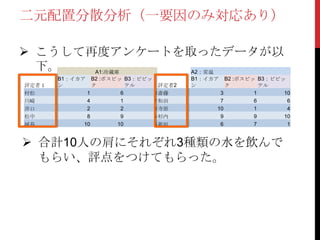
 こうして再度アンケートを取ったデータが以
下。 A1:冷蔵庫 A2：常温
評定者１
B1：イカア
ン
B2 :ボスビッ
ク
B3：ビビッ
テル 評定者2
B1：イカア
ン
B2 :ボスビッ
ク
B3：ビビッ
テル
村松 1 6 8 斎藤 3 1 10
川崎 4 1 2 和田 7 6 6
井口 2 2 8 寺原 10 1 4
松中 8 9 5 杉内 9 9 10
城島 10 10 3 新垣 6 7 1
 合計10人の肩にそれぞれ3種類の水を飲んで
もらい、評点をつけてもらった。

22. • Rで分析
#データの準備
set.seed(256) #乱数の再現
taste_points <- as.integer(runif(30 , min = 1 , max = 20))
#温度
temp <- factor(c(rep("refrige", 15), rep("normal_temp",15)))
#ボトル名
bottle_name <- factor(rep(c(rep("evian", 5), rep("volvic",5) , rep("vittel",5)),2))
#人の名前
name1 <- rep(c("村松","川崎","井口","松中","城島"),6)
name2 <- rep(c("斎藤","和田","寺原","杉内","新垣"),6)
total_name <- factor(c(name1 , name2))
二元配置分散分析（一要因のみ対応あり）

23. • Rで分析
summary(aov(taste_points~temp*bottle_name
+Error(total_name:temp+total_name:temp:bottle_name)))
二元配置分散分析（一要因のみ対応あり）
• ちょっと引数が足りなくないか？
• +Error(name+name:temp+name:bottle_name+name:temp:bottle_name)))
• 前回は人と人×温度、人×銘柄、人×温度×銘柄と3種類指定したのに
なぜ2種類で済んでいるのか？

24. • Rで分析
二元配置分散分析（一要因のみ対応あり）
A1:冷蔵庫 A2：常温
評定者１
B1：イカア
ン
B2 :ボスビッ
ク
B3：ビビッ
テル 評定者2
B1：イカア
ン
B2 :ボスビッ
ク
B3：ビビッ
テル
村松 1 6 8 斎藤 3 1 10
川崎 4 1 2 和田 7 6 6
井口 2 2 8 寺原 10 1 4
松中 8 9 5 杉内 9 9 10
城島 10 10 3 新垣 6 7 1
• 各評価者は同じ温度で3種類の銘柄を飲んでいます。つまり、人に対
して一貫して評価が高かったり、低かったする個人差の要因が現れ
ます。
• 個人差の要因である評定者と温度の違いの要因を表す温度がかかる
組みあわせだけ指定します。
⇛ でも、2要因とも対応ありの指定方法でも同じ結果が得られます。

25. • Rで分析
summary(aov(taste_points~temp*bottle_name
+Error(total_name:temp+total_name:temp:bottle_name)))
二元配置分散分析（一要因のみ対応あり）
人、温度、銘柄による違い
はなかった。
(温度・銘柄による違いは
5％に近い値）

26. 二元配置分散分析
• まとめ
1.二要因とも対応ありは＋Error（）で
要因の組合せを指定。
2.一要因のみ対応ありは、組合せを考え
ることで、＋Errorsの内容を減らせる。
（1.のやり方でも同じ結果）

27. ご静聴ありがとうございました