Recommended
PPTX
PPTX
PDF
PPTX
PDF
Cmdstanr入門とreduce_sum()解説
PDF
相関と因果について考える:統計的因果推論、その(不)可能性の中心
PDF
PPTX
PDF
PPTX
勾配ブースティングの基礎と最新の動向 (MIRU2020 Tutorial)
PPTX
PDF
PDF
PDF
PPTX
マルコフ連鎖モンテカルロ法 (2/3はベイズ推定の話)
PPTX
PDF
PDF
PDF
PDF
PDF
StanとRでベイズ統計モデリング読書会 導入編(1章~3章)
PPTX
PPTX
PDF
PDF
PPTX
Rで因子分析 商用ソフトで実行できない因子分析のあれこれ
PDF
PPTX
(実験心理学徒だけど)一般化線形混合モデルを使ってみた
PDF
PDF
More Related Content
PPTX
PPTX
PDF
PPTX
PDF
Cmdstanr入門とreduce_sum()解説
PDF
相関と因果について考える:統計的因果推論、その(不)可能性の中心
PDF
PPTX
What's hot
PDF
PPTX
勾配ブースティングの基礎と最新の動向 (MIRU2020 Tutorial)
PPTX
PDF
PDF
PDF
PPTX
マルコフ連鎖モンテカルロ法 (2/3はベイズ推定の話)
PPTX
PDF
PDF
PDF
PDF
PDF
StanとRでベイズ統計モデリング読書会 導入編(1章~3章)
PPTX
PPTX
PDF
PDF
PPTX
Rで因子分析 商用ソフトで実行できない因子分析のあれこれ
PDF
PPTX
(実験心理学徒だけど)一般化線形混合モデルを使ってみた
Viewers also liked
PDF
PDF
PDF
PDF
MCMCサンプルの使い方 ~見る・決める・探す・発生させる~
ODP
PDF
PPTX
PDF
スパースモデリング、スパースコーディングとその数理(第11回WBA若手の会)
PDF
PDF
Similar to MCMCによる回帰分析@ベイズセミナー
PDF
PPTX
PDF
データ解析のための統計モデリング入門9章後半
PDF
データ解析のための統計モデリング入門9章後半
PPTX
PDF
PDF
PDF
PDF
RBM、Deep Learningと学習(全脳アーキテクチャ若手の会 第3回DL勉強会発表資料)
PDF
RStanとShinyStanによるベイズ統計モデリング入門
PDF
Monte Carlo Methods (Chapter 17 in Deep learning by Ian Goodfellow)
PDF
PPTX
第7回 KAIM 金沢人工知能勉強会 回帰分析と使う上での注意事項
PDF
PDF
ベイズ推定でパラメータリスクを捉える&優れたサンプラーとしてのMCMC
PDF
東京都市大学 データ解析入門 6 回帰分析とモデル選択 1
PDF
PPTX
MCMC and greta package社内勉強会用スライド
PDF
東京都市大学 データ解析入門 7 回帰分析とモデル選択 2
PPTX
【DBDA勉強会2013】Doing Bayesian Data Analysis Chapter 16: Metric Predicted Variab...
More from Takashi Yamane
PPTX
PPTX
DiagrammeRと仲良くなった話ーグラフィカルモデルのためのDiagrammeR速習ー
PPTX
PPTX
PPTX
PDF
PDF
PPTX
PPTX
PPTX
PPT
PDF
PDF
MCMCによる回帰分析@ベイズセミナー 1. 2. 自己紹介
氏名 : 山根 嵩史
所属 : 広島大学大学院 教育学研究科
教育人間科学専攻 学習心理学研究室 (D2)
研究テーマ : メタ記憶,読解方略
Mail : t.yamane1969@gmail.com
Twitter : @T_Yamane
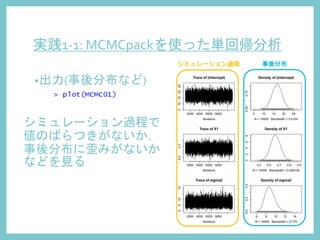
3. 4. 5. 6. 実践1-1: MCMCpackを使った単回帰分析
•MCMCpackのMCMCregress()関数を使用
MCMCregress(formula, data, burnin = 1000, mcmc = 10000,
thin = 1, verbose = 0, seed = NA, beta.start = NA,
b0 = 0, B0 = 0, c0 = 0.001, d0 = 0.001,
sigma.mu = NA, sigma.var = NA,
marginal.likelihood = c("none", "Laplace", "Chib95"), ...)
formula: 回帰モデル, data: データの指定
burnin: バーンイン期間, mcmc: 繰り返し回数
7. 実践1-1: MCMCpackを使った単回帰分析
•MCMCpackのMCMCregress()関数を使用
MCMCregress(formula, data, burnin = 1000, mcmc = 10000,
thin = 1, verbose = 0, seed = NA, beta.start = NA,
b0 = 0, B0 = 0, c0 = 0.001, d0 = 0.001,
sigma.mu = NA, sigma.var = NA,
marginal.likelihood = c("none", "Laplace", "Chib95"), ...)
thin: 推定に用いる値のサンプリング間隔
verbose: 途中経過を表示するタイミング
seed: シード値の設定
8. 実践1-1: MCMCpackを使った単回帰分析
•MCMCpackのMCMCregress()関数を使用
MCMCregress(formula, data, burnin = 1000, mcmc = 10000,
thin = 1, verbose = 0, seed = NA, beta.start = NA,
b0 = 0, B0 = 0, c0 = 0.001, d0 = 0.001,
sigma.mu = NA, sigma.var = NA,
marginal.likelihood = c("none", "Laplace", "Chib95"), ...)
b0: 事前分布の平均, B0: 事前分布の分散
c0: 逆ガンマ分布のshapeパラメータ
d0: 逆ガンマ分布のscaleパラメータ
(その他の引数については参考文献[1]を参照)
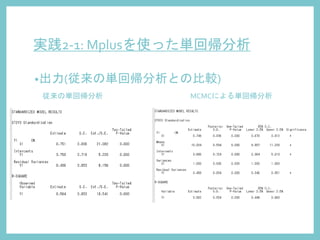
9. 10. 11. 12. 13. 14. 15. 16. 17. 18. 19. 20. 実践2-1: Mplusを使った単回帰分析
•入力 従来の単回帰分析 MCMCによる単回帰分析
ANALYSISコマンドにおいて
“ESTIMATOR = BAYS”でベイズ推定を指定
“POINT = MEDIAN” で推定する値を指定
“CHAIN = 3”でマルコフ連鎖の数を指定
“BITERATIONS = (10000)”でシミュレーション回数を指定
21. 22. 23. 24. 25. 26. 27. Let’s
Bayes!
参考文献
[1]Martin,A. A. D., Quinn, K. M., Park, J. H., Jong, M., & Park, H.
(2013). Package “ MCMCpack ”, (Mcmc).
[2]小杉考司・清水裕士 (編著) (2014). MplusとRによる
構造方程式モデリング入門 北大路書房, pp. 245-261
Editor's Notes #3 ・声量確認 #5 ・当然Rとmplusをお使いですよね?







![実践1-1: MCMCpackを使った単回帰分析
•MCMCpackのMCMCregress()関数を使用
MCMCregress(formula, data, burnin = 1000, mcmc = 10000,
thin = 1, verbose = 0, seed = NA, beta.start = NA,
b0 = 0, B0 = 0, c0 = 0.001, d0 = 0.001,
sigma.mu = NA, sigma.var = NA,
marginal.likelihood = c("none", "Laplace", "Chib95"), ...)
b0: 事前分布の平均, B0: 事前分布の分散
c0: 逆ガンマ分布のshapeパラメータ
d0: 逆ガンマ分布のscaleパラメータ
(その他の引数については参考文献[1]を参照)](https://image.slidesharecdn.com/mcmc-140609001607-phpapp01/85/MCMC-8-320.jpg)












![実践2-1: Mplusを使った単回帰分析
•出力(シミュレーション過程と事後分布)
出力画面で[plot]→[view plot]からチェック
シミュレーション過程
(Bayesian posterior parameter trace plots)
事後分布
(Bayesian posterior parameter distributions)](https://image.slidesharecdn.com/mcmc-140609001607-phpapp01/85/MCMC-22-320.jpg)


![Let’s
Bayes!
参考文献
[1]Martin,A. A. D., Quinn, K. M., Park, J. H., Jong, M., & Park, H.
(2013). Package “ MCMCpack ”, (Mcmc).
[2]小杉考司・清水裕士 (編著) (2014). MplusとRによる
構造方程式モデリング入門 北大路書房, pp. 245-261](https://image.slidesharecdn.com/mcmc-140609001607-phpapp01/85/MCMC-27-320.jpg)