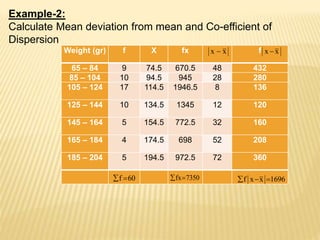
This document provides examples and formulas for calculating mean absolute deviation and coefficient of dispersion. Mean absolute deviation is a measure of how far data points deviate from the mean. It is calculated by taking the average of the absolute differences between each data point and the mean. Coefficient of dispersion is calculated by dividing the mean absolute deviation by the mean and multiplying by 100 to express it as a percentage. Two examples are provided to demonstrate calculating mean absolute deviation and coefficient of dispersion using data sets and frequency distributions.

1. Mean absolute deviation from mean
NADEEM UDDIN
ASSOCIATE PROFESSOR
OF STATISTICS

2. Mean Absolute Deviation:
A good measure of dispersion should consider
differences of all observations from the mean.
If we simply average all differences from the
mean, the positives and the negatives will
cancel out, even though they both contribute
to dispersion, and the resulting average will
equal zero. The mean absolute
deviation (MAD) is an average of the absolute
differences between the observations and
central value such as mean median or mode.

3. Formula Mean Absolute Deviation about mean:
Coefficient of Mean Deviation( x )
  100
.

x
xDM

4. Example-1: 2, 4, 6, 8, 10
(a) Find Mean absolute deviation from mean.
(b) Find Co-efficient of Dispersion.
Solution: First find mean
6
5
108642





n
x
X
2
4
6
8
10
X XX 
462 
264 
066 
268 
4610 
12XX 

5. DO YOURSELF
1-For the following data
6, 12, 18, 24, 30
(i)Calculate mean absolute deviation about
mean.(7.2)
(ii) Calculate coefficient of dispersion.(40%)
2-For the following set of data
7, 2, 9, 11, 12, 4, 5
(i)Calculate mean absolute deviation about
mean.(3.02)
(ii) Calculate coefficient of dispersion.(42.30%)

6. (a) 4.2
5
12
n
XX
)X(D.M 


100
x
)x(D.M

100
6
4.2

%40
(b)Co-efficient of Dispersion =
=
=

7. Example-2:
Calculate Mean deviation from mean and Co-efficient of
Dispersion
Weight (gr) f X fx f
65 – 84 9 74.5 670.5 48 432
85 – 104 10 94.5 945 28 280
105 – 124 17 114.5 1946.5 8 136
125 – 144 10 134.5 1345 12 120
145 – 164 5 154.5 772.5 32 160
165 – 184 4 174.5 698 52 208
185 – 204 5 194.5 972.5 72 360
xx  xx 
60f  7350fx 1696xxf 

8. First find mean
g5.122
60
7350
f
fx
x 



1696
. ( ) 28.27
60
. ( )
100
28.27
100 23.08%
122.5
f x x
M D x g
f
M D x
Coefficient of Dispersion
x
 
  

 
  

9. Time(secon
d)
10-14 15-19 20-24 25-29
F 3 5 10 7
Height
(Inch)
60 61 62 63 64 65 66 67 68 69 70
No.of
Student
2 4 9 10 12 20 18 12 9 6 5
DO YOURSELF
1. Time taken by a group of 25 students to solve a problem.
(i)Calculate mean absolute deviation about mean.(3.89)
(ii) Calculate coefficient of dispersion.(18.35%)
2. From the following frequency distribution, find out mean height
Of the students.
(i)Calculate mean absolute deviation about mean.(1.92)
(ii) Calculate coefficient of dispersion.(2.94%)