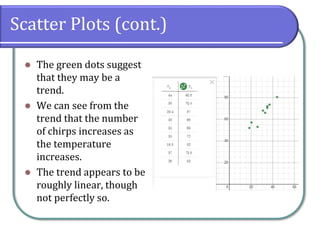
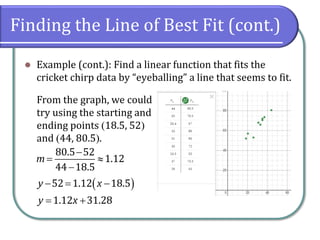
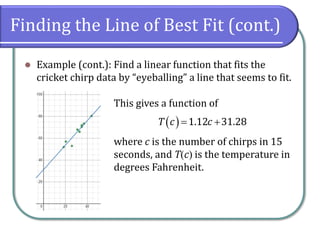
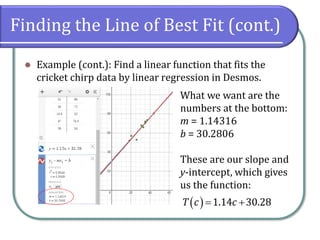
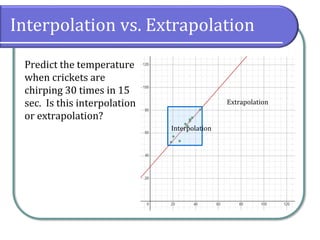
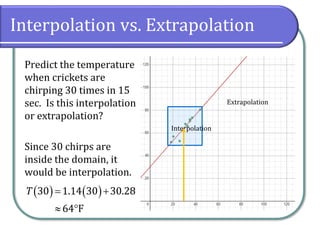
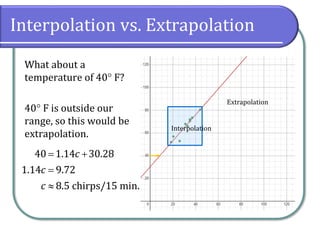
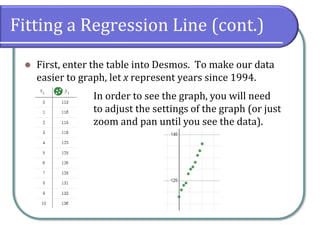
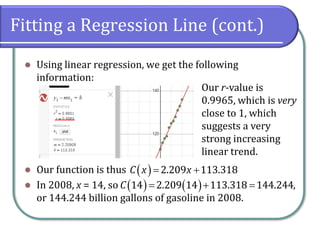
This document discusses fitting linear models to data, including how to create and interpret scatter plots, find the line of best fit, and differentiate between interpolation and extrapolation. It provides examples using cricket chirping data and gasoline consumption trends, emphasizing the importance of correlation coefficients in assessing linearity. Additionally, it includes instructions for using graphing utilities like Desmos to model data and make predictions.