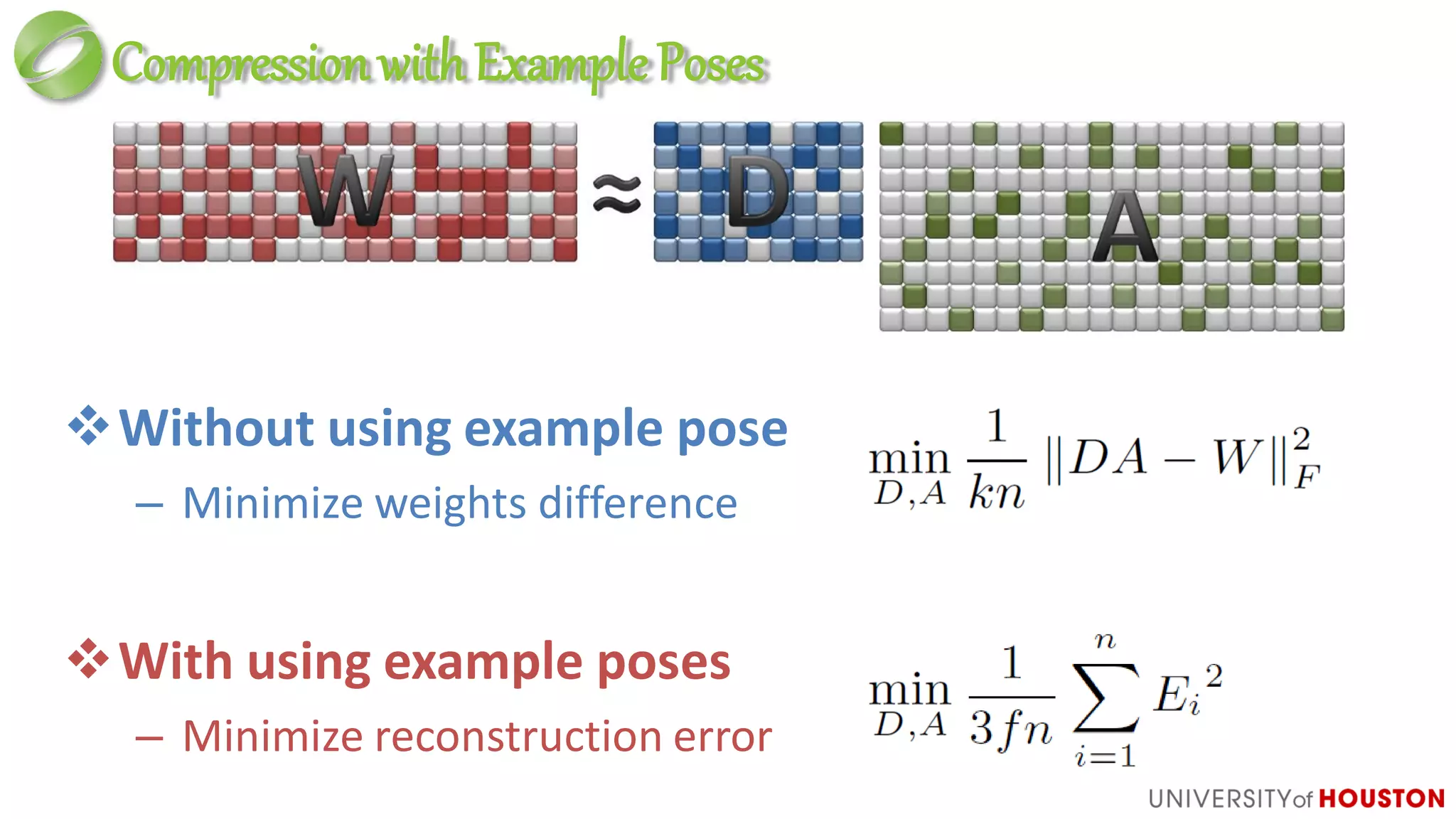
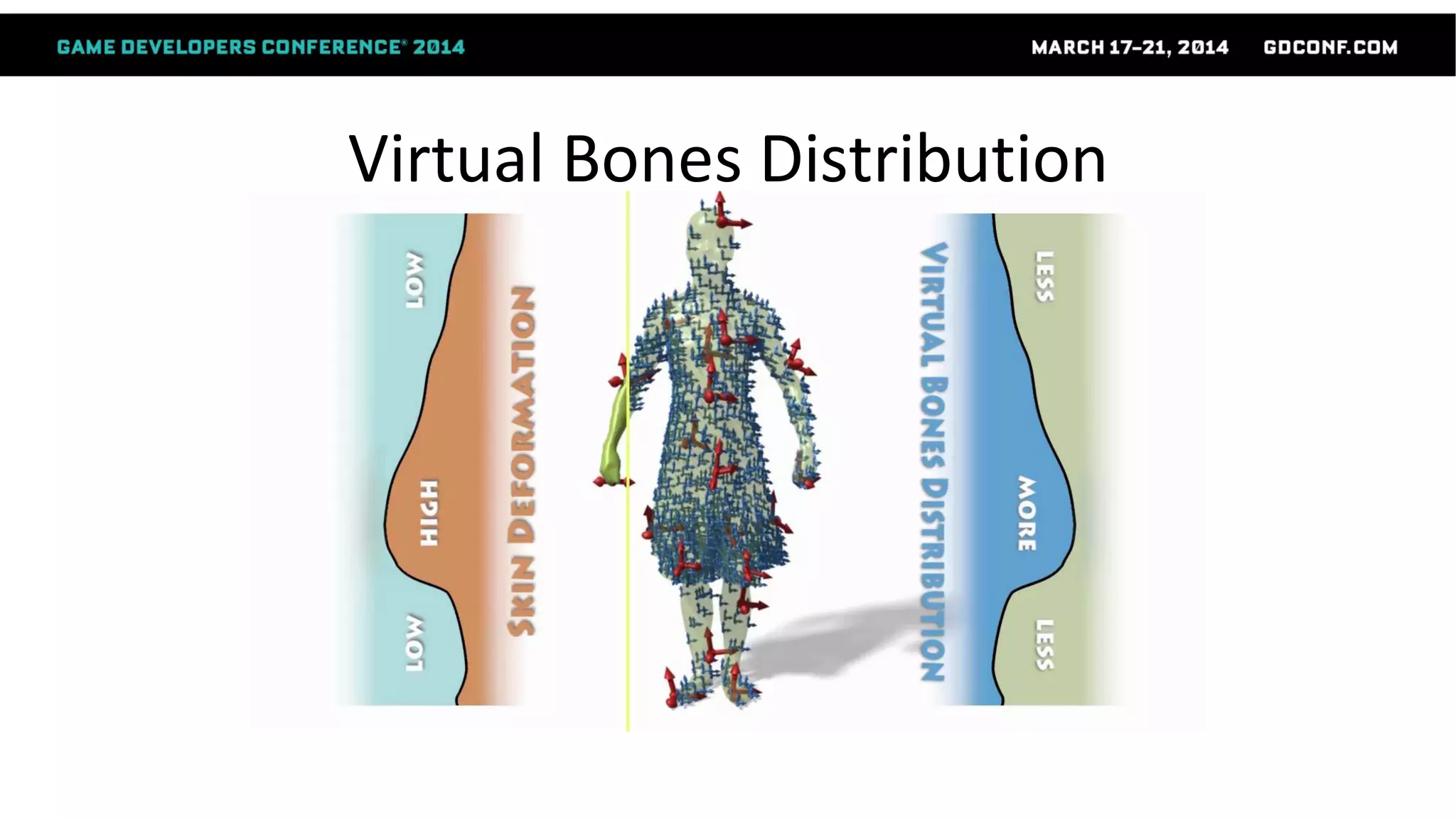
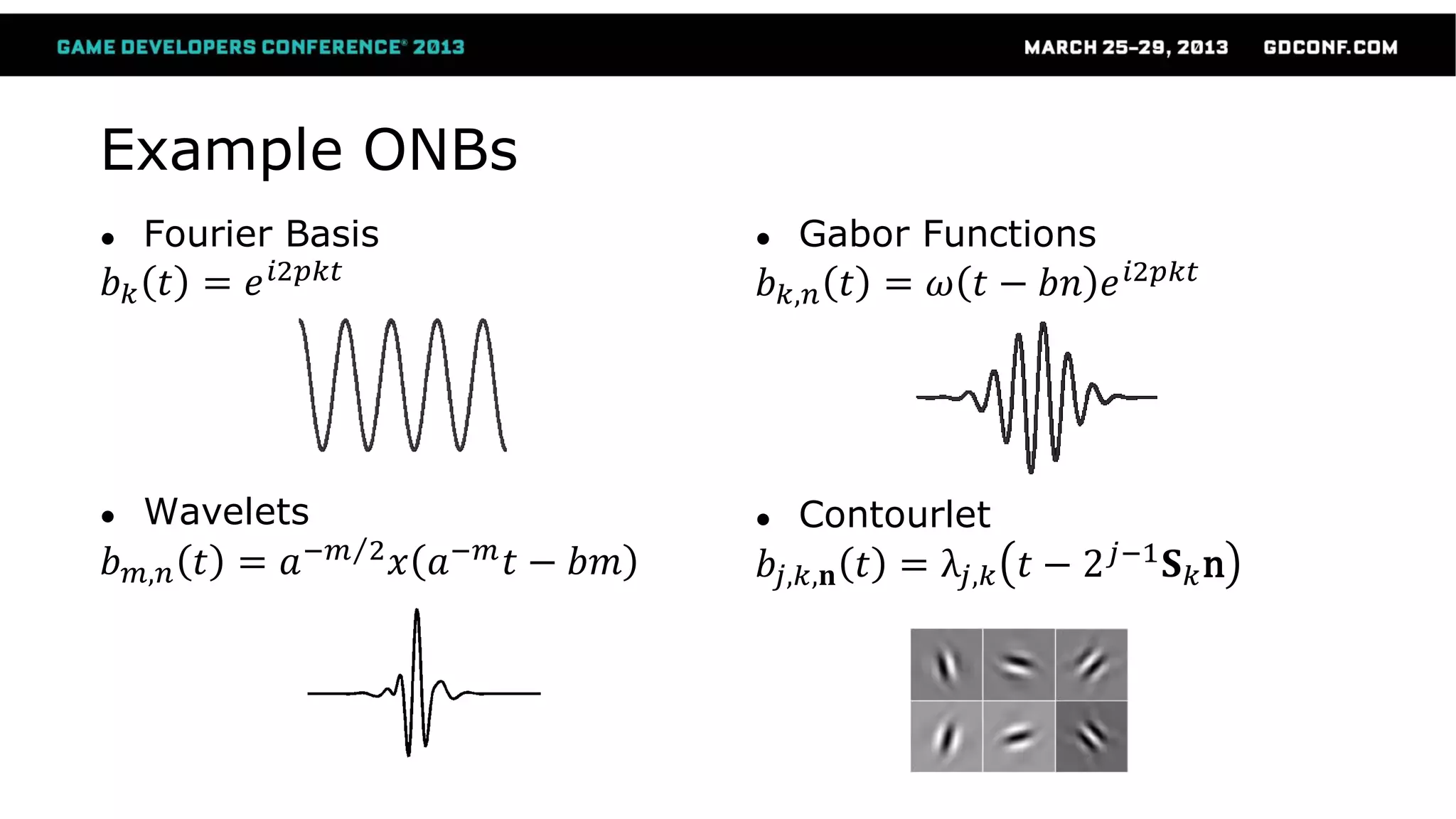
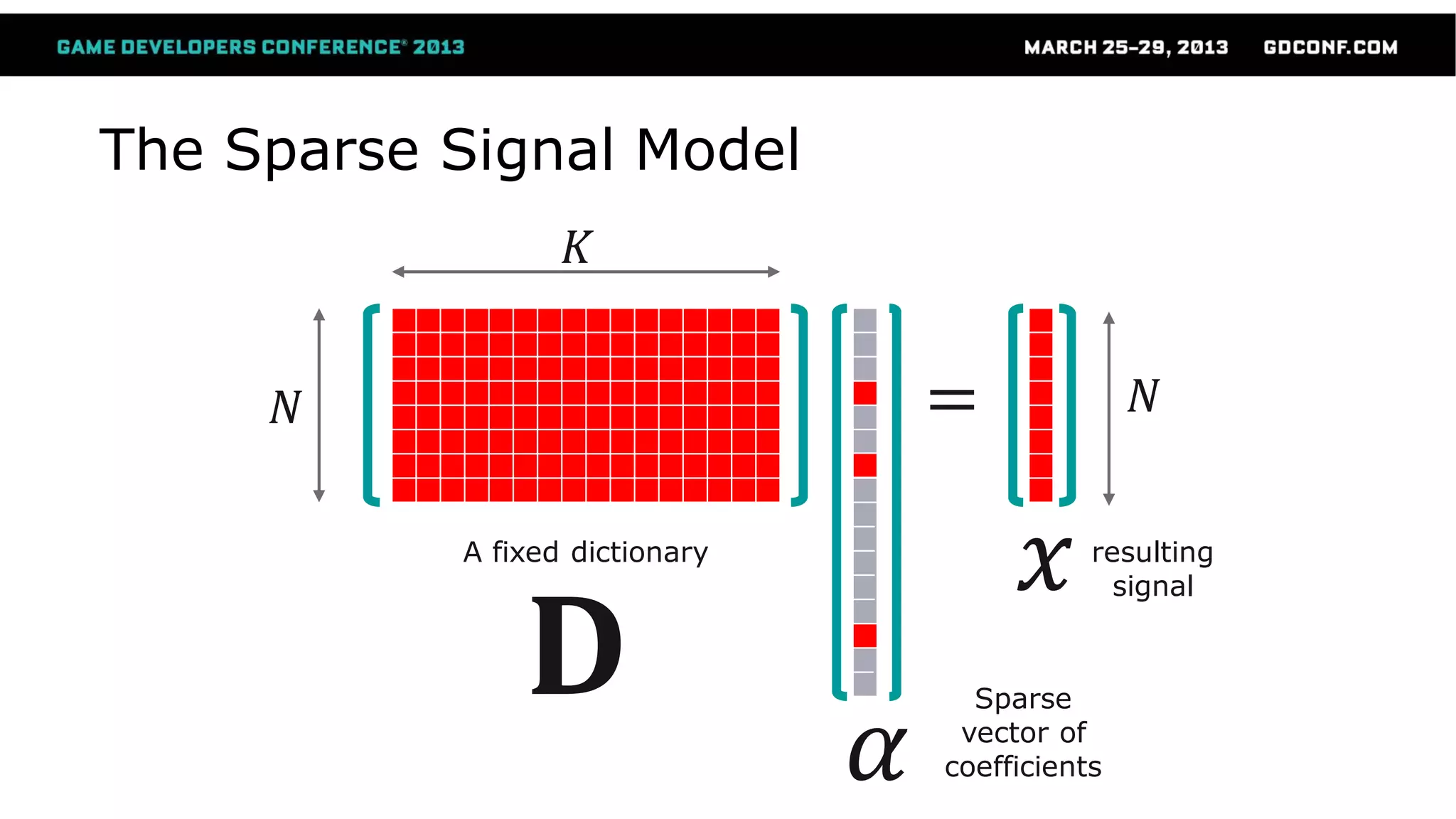
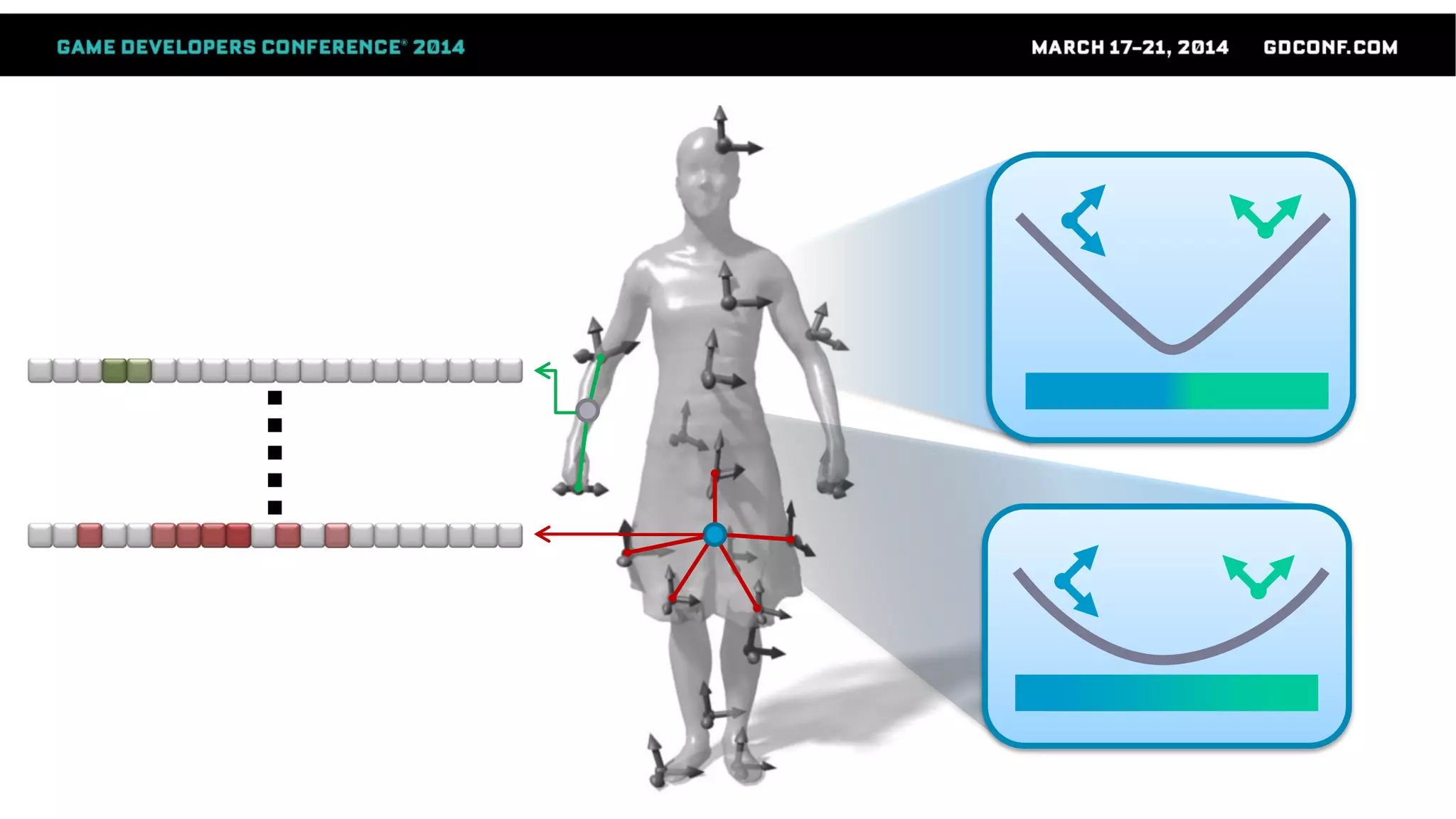
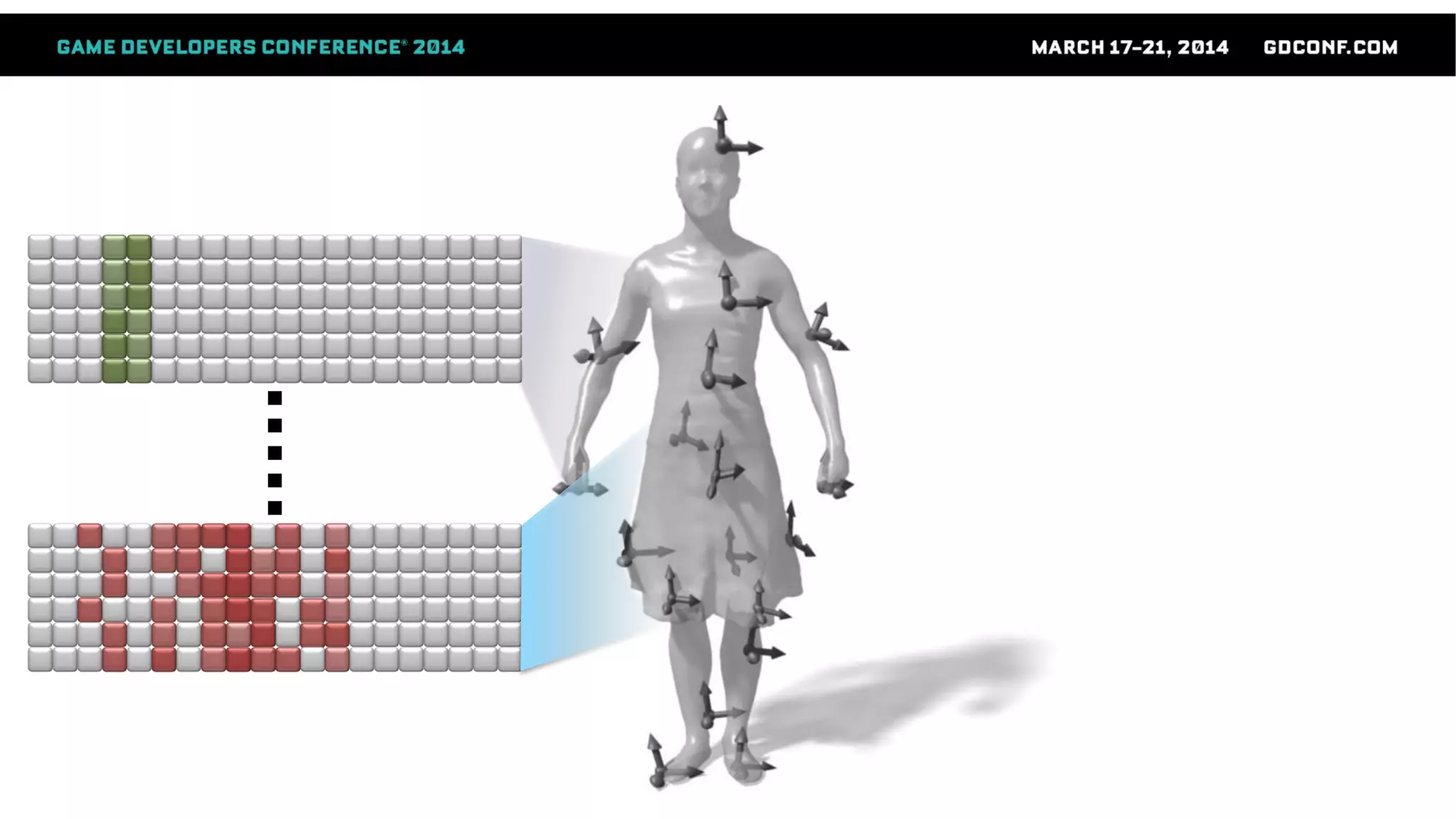
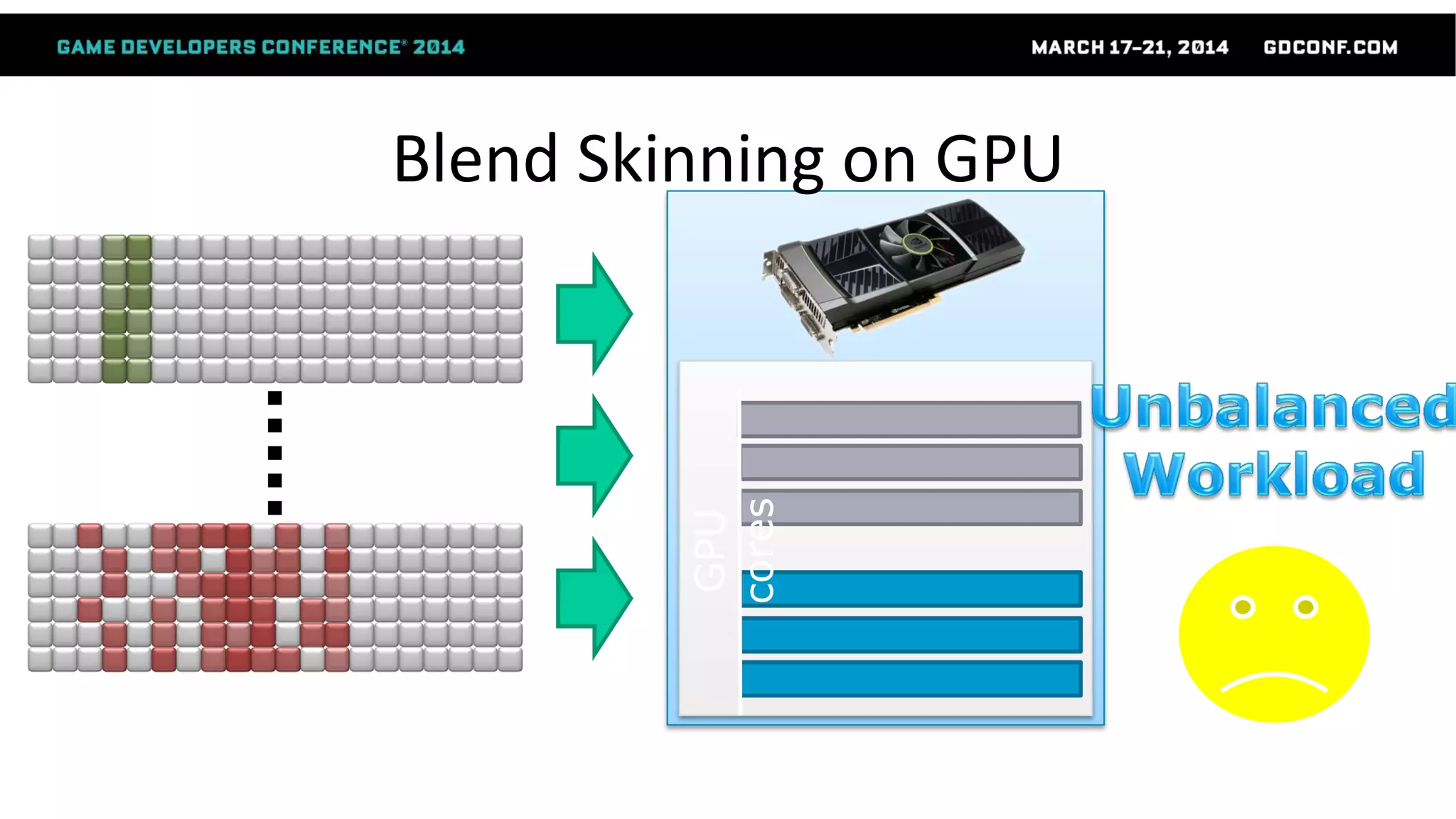
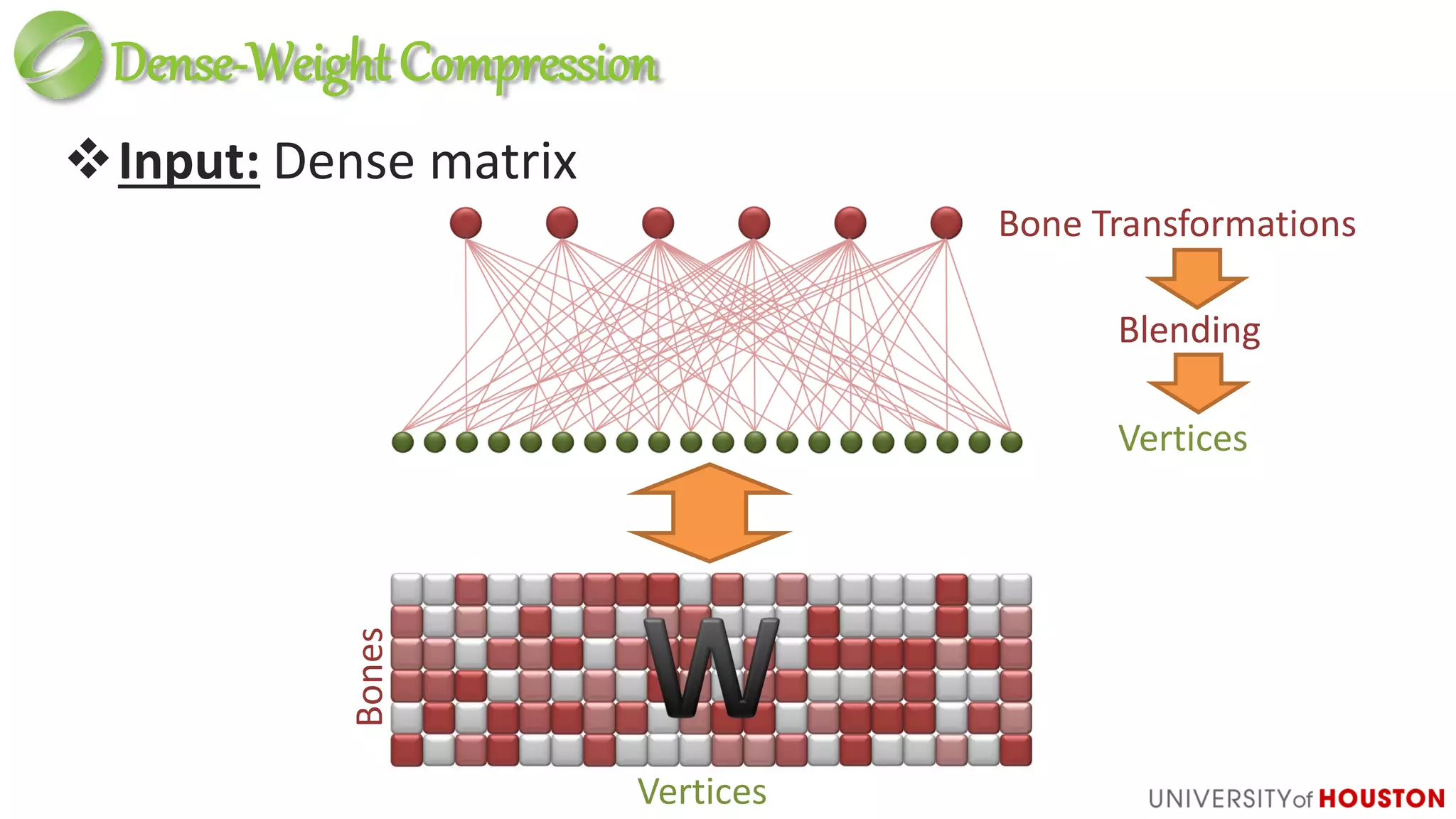
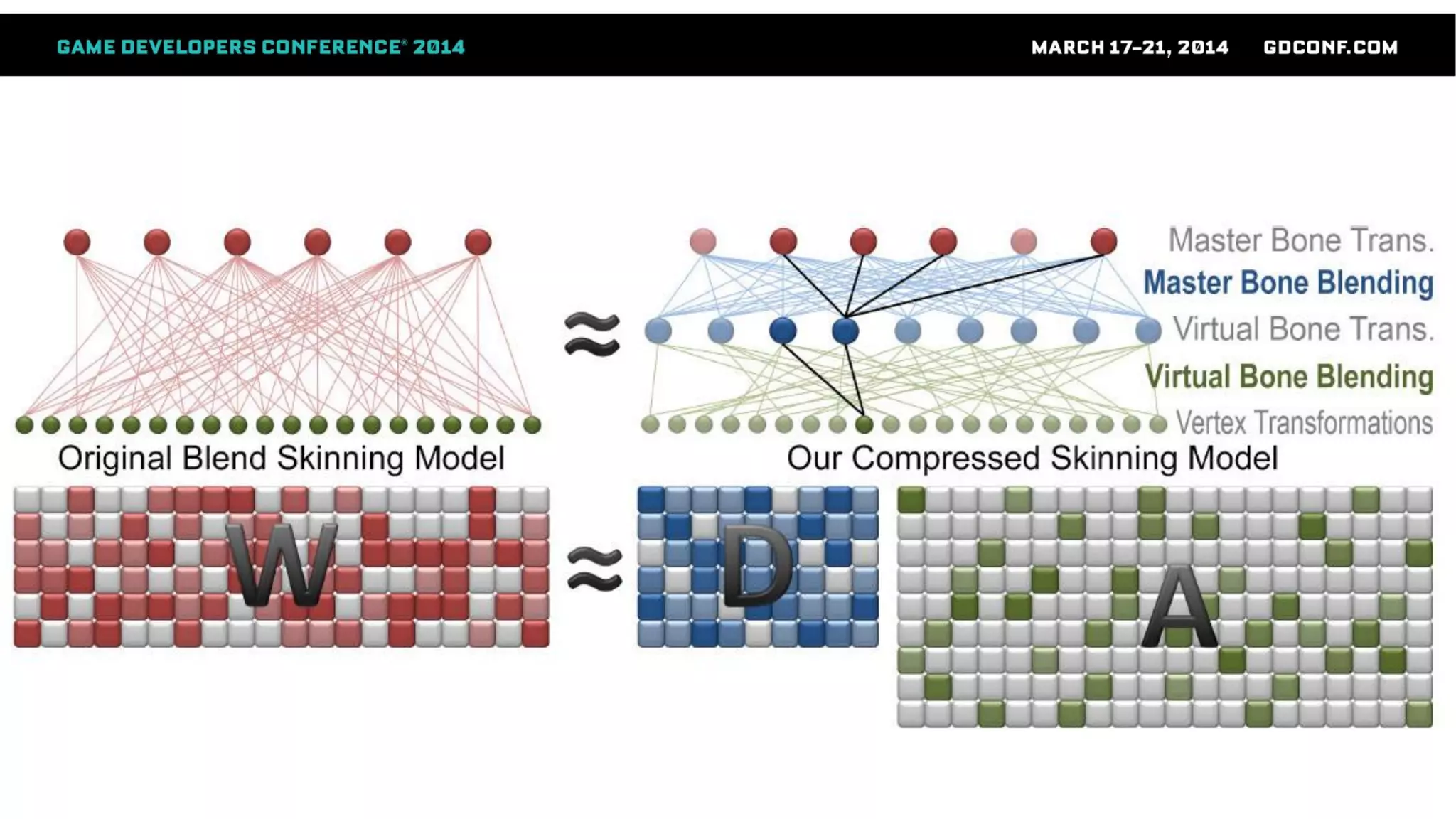
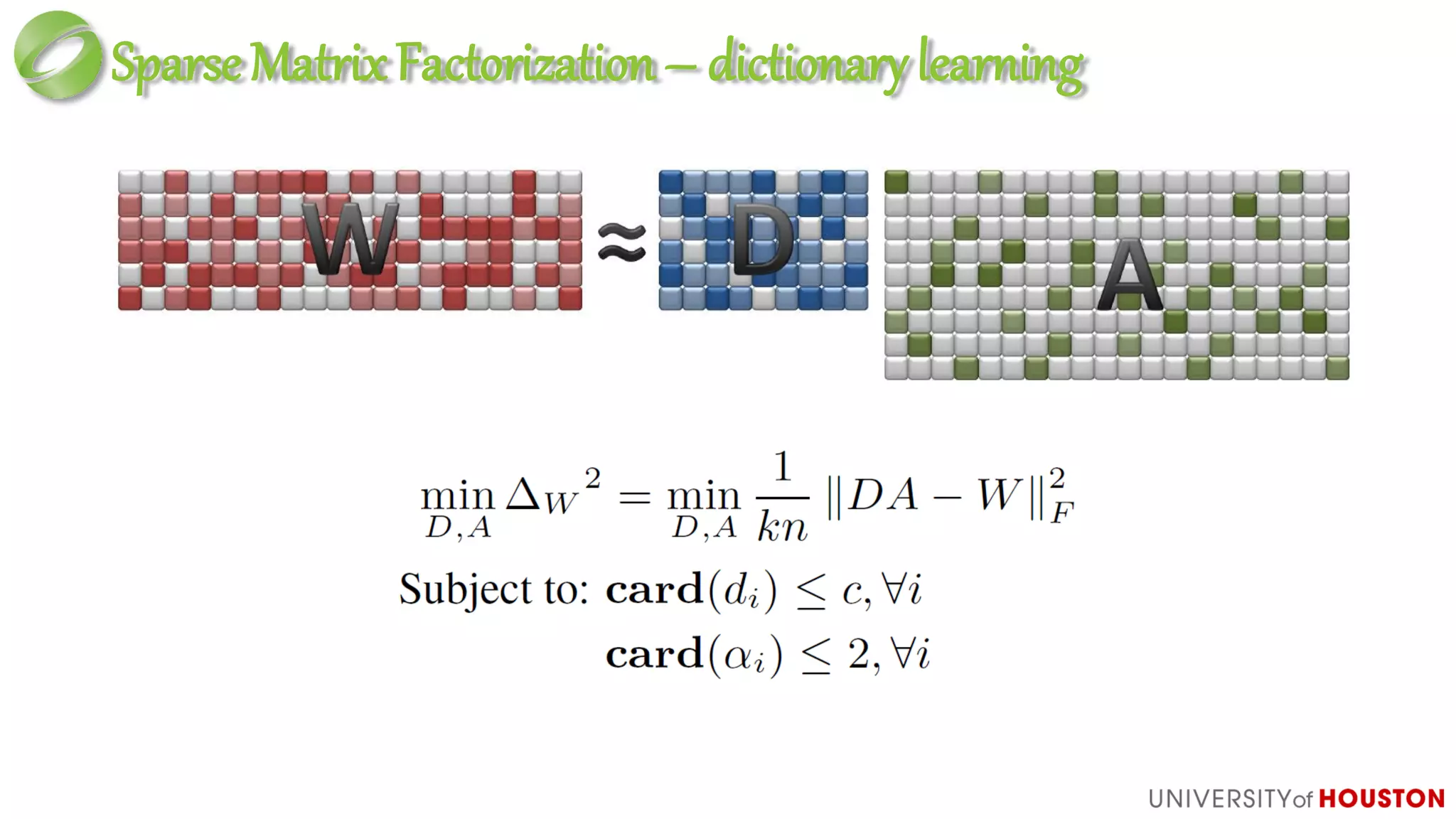
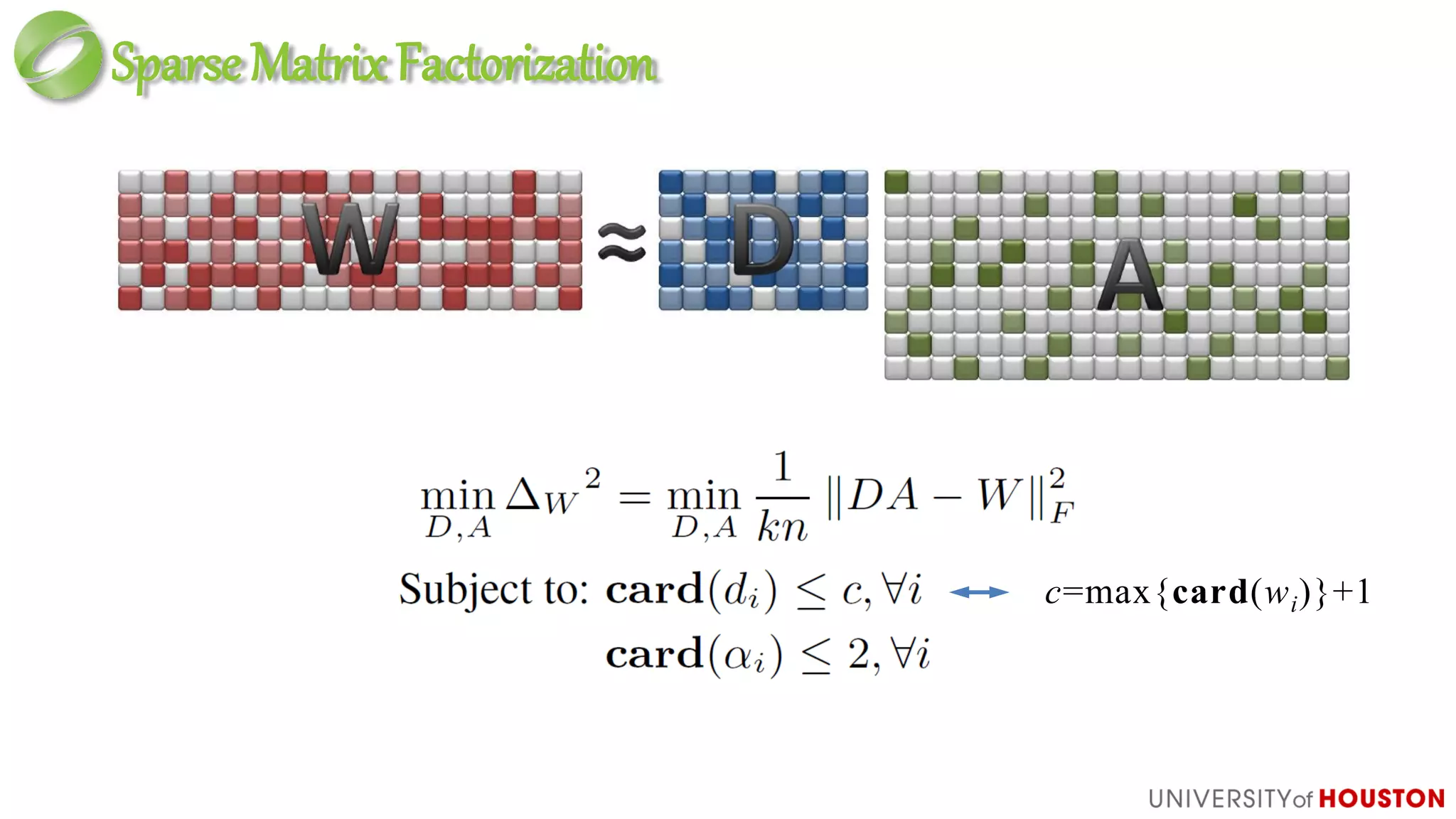
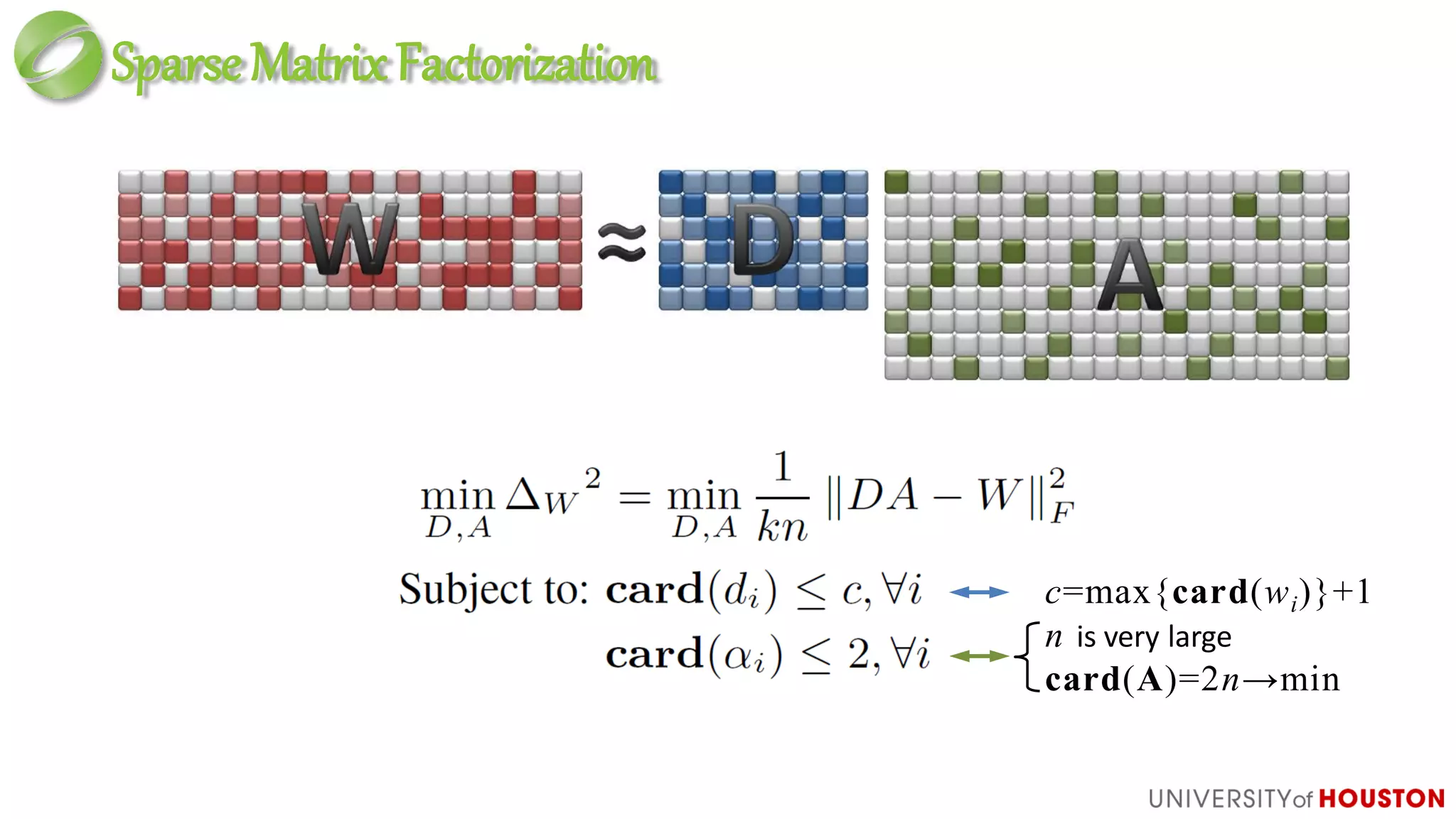
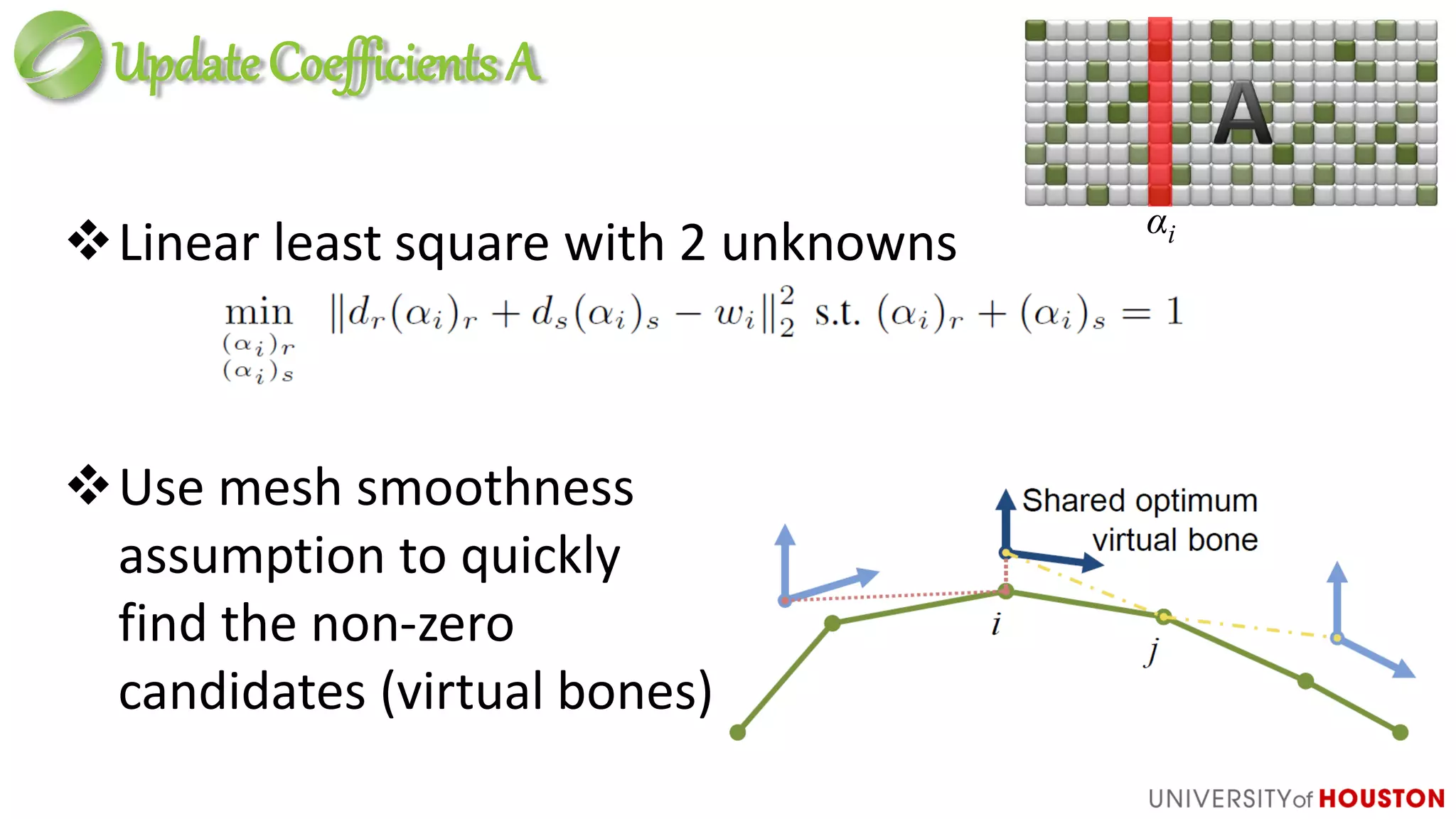
This document discusses advanced techniques in compressing skinned animations for games, focusing on methods like K-SVD and dictionary learning. It outlines the benefits of using overcomplete dictionaries for sparse representation and introduces a two-layer sparse compression approach that leverages virtual bones to enhance animation efficiency. The presentation also emphasizes the importance of modern sparsity methods and their applications in improving animation quality while maintaining low computational costs.























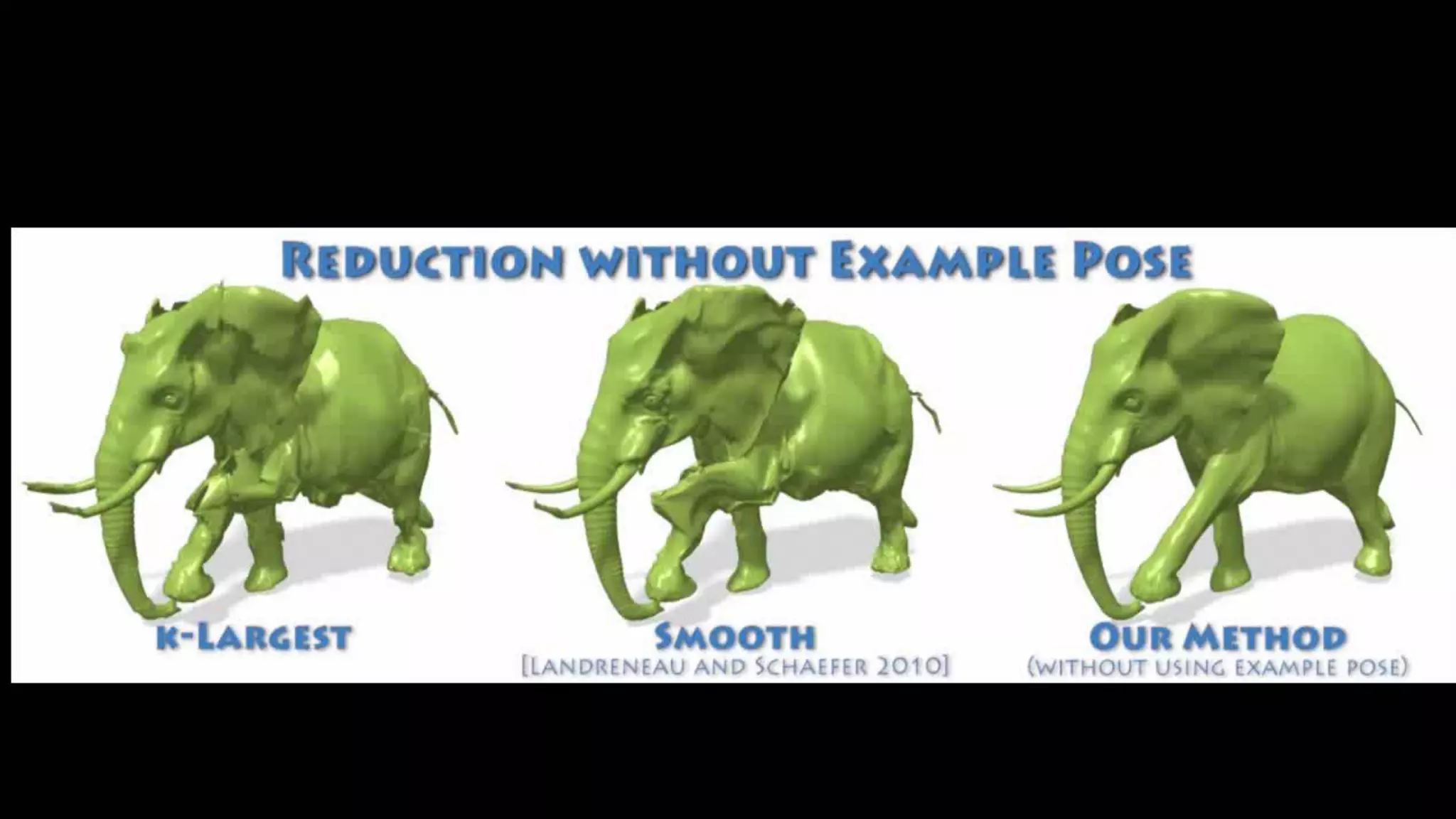
![WeightsReduction
Poisson-based Weight Reduction of Animated Meshes [Landreneau and Schaefer 2010]
Discrete optimization:
– Impossible to find optimum solution
– Very high cost for non-optimum solution
• Fracture
• Significant increase of computing cost: nK non-zero n(K+1) non-zero](https://image.slidesharecdn.com/dictionarylearningingames-ko-draft7-gdc14mathforgames-140316150414-phpapp02/75/Dictionary-Learning-in-Games-GDC-2014-29-2048.jpg)












![Atom Updates
Atom update:
foreach vertex
● update each atom to minimize error for the set of vertices that
reference it (this is like K-SVD)
● Miral’s Online Dictionary Learning [Miral09]](https://image.slidesharecdn.com/dictionarylearningingames-ko-draft7-gdc14mathforgames-140316150414-phpapp02/75/Dictionary-Learning-in-Games-GDC-2014-49-2048.jpg)