The document provides an analysis and design of algorithms focusing on linear time sorting methods, specifically bucket sort, radix sort, and counting sort. It describes the mechanisms, time complexities, pros, and cons of each sorting algorithm. Each method is evaluated based on its assumptions, implementation steps, and performance considerations.

1. Subject : Analysis and design of algorithms(2150703)
Branch : Information Technology Batch : 1D16
Academic Year : 2018-2019(Odd)
Topic : Sorting in linear time(Bucket,radix,counting sort)
Prepared by:-
Prakshal Trivedi (160110116055)
Tejoy Vachhrajani (160110116057)
Bhavik vashi (160110116061)
G. H. Patel College of
Engineering & Technology

2. Radix Sort
• Radix sort is non comparative sorting
method
• Two classifications of radix sorts are least
significant digit (LSD) radix sorts and most
significant digit (MSD) radix sorts.
• LSD radix sorts process the integer
representations starting from the least digit
and move towards the most significant digit.
MSD radix sorts work the other way around.

3. 329 720 720 329
457 355 329 355
657 436 436 436
839 457 839 457
436 657 355 657
720 329 457 720
355 839 657 839
Radix Sort
In input array A, each element is a number of d digit.
Radix -Sort(A,d)
for i  1 tod
do"use a stable sort to sort array Aon digit i”;

4. Time Complexity Analysis
Given n d-digit number in which each digit can
take up to k possible values, RADIX-SORT
correctly sorts these numbers in Ө(d(n+k))
time if the stable sort it uses takes Ө(n+k)
time.

5. Radix Sort Review
•
•
•
•
Assumption: input taken from large set of numbers
Basic idea:
– Sort the input on the basis of digits starting from unit’s
place.
– This gives the position of that number – similar to selection
sort.
Pro’s:
– Fast
– Asymptotically fast - O(d(n+k))
–Simple to code
Con’s:
– Doesn’t sort in place.

6. Bucket Sort
 Bucket sort assumes that the input is generated by a random
process and drawn from a uniform distribution.
 In other words the elements are distributed uniformly and
independently over the interval [0,1].
 Bucket sort divides the interval [0,1] into n equal sized
subintervals or buckets. Then distributes the n inputs into
these buckets.
 After that the elements of each buckets are sorted using a
sorting algorithm generally using insertion or quick sort.
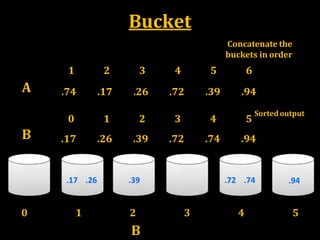
 Finally the buckets are concatenated together in order.
 Consider that the input is an n-element array A and each
element A[i] in the array satisfies the 0<=A[i]<1

7. Bucket Sort Algorithm
 Bucket-Sort(A)
1. Let B[0….n-1] be a new array
2. n = length[A]
3. for i = 0 to n-1
4. make B[i] an empty list
5. for i = 1 to n
6. do insert A[i] into list B[  n A[i]  ]
7. for i = 0 to n-1
8. do sort list B[i] with Insertion-Sort
9. Concatenate lists B[0], B[1],…,B[n-1] together in
order

8. Bucket
A
1 2 3 4 5 6
.74 .17 .26 .72 .39 .94

9. Bucket: Loop 1
A
n=6
1 2 3 4 5 6
.74 .17 .26 .72 .39 .94
0 1 2
B
3 4 5

10. Bucket: Loop 2
A
2 3 4 5 6
.17 .26 .72 .39 .94
B[  n A[i]  ] = B[  6X.74  ]=B[  4.44  ]=B[4]
0 1 2
B
3 4 5
FOR n=6, i=1
1
.74

11. Bucket: Loop 2
A
1
.74
3 4 5 6
.26 .72 .39 .94
B[  n A[i]  ] = B[  6X.17  ]=B[  1.02  ]=B[1]
FOR n=6, i=2
.74
2
.17
0 1 2
B
3 4 5

12. Bucket: Loop 2
A
1 2
.74 .17
4 5 6
.72 .39 .94
B[  n A[i]  ] = B[  6X.26  ]=B[  1.56  ]=B[1]
FOR n=6, i=3
.74
3
.26
.17
0 1 2
B
3 4 5

13. Bucket: Loop 2
A
1 2 3
.74 .17 .26
5 6
.39 .94
B[  n A[i]  ] = B[  6X.72  ]=B[  4.32  ]=B[4]
FOR n=6, i=4
.74
4
.72
.26
.17
0 1 2
B
3 4 5

14. Bucket: Loop 2
A
1 2 3 4
.74 .17 .26 .72
6
.94
B[  n A[i]  ] = B[  6X.39  ]=B[  2.34  ]=B[2]
FOR n=6, i=5
5
.39
.17
.26 .74
.72
0 1 2
B
3 4 5

15. Bucket: Loop 2
A
1 2 3 4 5
.74 .17 .26 .72 .39
B[  n A[i]  ] = B[  6X.94  ]=B[  5.64  ]=B[5]
FOR n=6, i=6
6
.94
.17
.26 .74
.72.39
0 1 2
B
3 4 5

16. Bucket: End of Loop 2
A
1 2 3 4 5 6
.74 .17 .26 .72 .39 .94
.17
.26 .74
.72.39 .94
0 1 2
B
3 4 5

17. Bucket: Loop 3
A
Apply insertion sort
on each bucket
1 2 3 4 5 6
.74 .17 .26 .72 .39 .94
0 1 2
B
3 4 5
.17 .26 .72 .74 .94.39

18. Bucket
A
Concatenate the
buckets in order
1 2 3 4 5 6
.74 .17 .26 .72 .39 .94
0 1 2
B
3 4 5
.17 .26 .72 .74 .94.39
B
0 1 2 3 4 5
Sortedoutput
.17 .26 .39 .72 .74 .94

19. Analysis of Bucket Sort
1. Let B[0….n-1] be a new array
2. n = length[A]
3. for i = 0 to n-1
4. make B[i] an empty list
5. for i = 1 to n
6. do insert A[i] into list B[ floor of n A[i] ]
7. for i = 0 to n-1
 Bucket-Sort(A)
8. do sort list B[i] with Insertion-Sort
9. Concatenate lists B[0], B[1],…,B[n-1] together in
order
Step 5 and 6
takes O(n)
time
Step 7 and 8
takes O(n
log(n/k) time
Step 9 takes
O(k) time
In total Bucket sort takes : O(n) (if k=Θ(n))

20. Bucket Sort Review
•
•
•
•
Assumption: input is uniformly distributed across a range
Basic idea:
–Partition the range into a fixed number of buckets.
–Toss each element into its appropriate bucket.
–Sort each bucket.
Pro’s:
– Fast
– Asymptotically fast (i.e., O(n) when distribution is uniform)
– Simple to code
–Good for a rough sort.
Con’s:
– Doesn’t sort in place.

21. Counting sort
 Counting sort assumes that each of the n input elements is an
integer in the range 0 to k. that is n is the number of elements and
k is the highest value element.
 Consider the input set : 4, 1, 3, 4, 3. Then n=5 and k=4
 Counting sort determines for each input element x, the number of
elements less than x. And it uses this information to place
element x directly into its position in the output array. For
example if there exits 17 elements less that x then x is placed into
the 18th position into the output array.
 The algorithm uses three array:
Input Array: A[1..n] store input data where A[j]  {1, 2, 3, …, k}
Output Array: B[1..n] finally store the sorted data
Temporary Array: C[1..k] store data temporarily

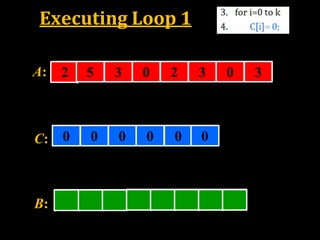
22. Counting Sort
1. Counting-Sort(A, B, k)
2. Let C[0…..k] be a new array
3. for i=0 to k
4. C[i]= 0;
5. for j=1 to A.length or n
6. C[ A[j] ] = C[ A[j] ] + 1;
7. for i=1 to k
8. C[i] = C[i] + C[i-1];
9. for j=n or A.length down to 1
10. B[ C[ A[j] ] ] = A[j];
11. C[ A[j] ] = C[ A[j] ] - 1;

23. Counting-sort example
A:
1 2 3 4 5
C:
1 2 3 4
6 7 8
5 3 0 2 3 0 35 3 0 2 3 0 3
0 5
B:
1 2 3 4 5 6 7 8

24. Executing Loop 1
A:
1 2 3 4 5
C:
1 2 3 4
6 7 8
5 3 0 2 3 0 35 3 0 2 3 0 3
0 0 0 0 0
0
00 0 0 0 0 0
5
1 2 3 4 5 6 7 8
B:

25. Executing Loop 2
A:
1 2 3 4 5
C:
1 2 3 4
6 7 8
5 3 0 2 3 0 35 3 0 2 3 0 3
0 0 0 0
0
00 0 1 0 0 0
5
1 2 3 4 5 6 7 8
B:

26. End of Loop 2
A:
1 2 3 4 5
C:
1 2 3 4
6 7 8
5 3 0 2 3 0
2 0 2 0
0
1
5
1 2 3 4 5 6 7 8
32 0 2 3 0 1
35 3 0 2 3 0 3
B:

27. End of Loop 3
A:
B:
1 2 8
5 3 0 2 3 0
1 2 3 4 5 6 7 8
3
3 4 5 6 7
5 3 0 2 3 0 3
C: 2 4
1 2 3 40 5
22 2 4 77 7 87 8

28. End of Loop 4
A:
B:
1 2 3 8
1 2 3 4 5 6 7 8
C:
1 2 3 40 5
2 7
3
3
0
0
3
30 2
3
3
0
5
4 5 6 7
5 3 0 3 0 3
4
5
2 70 2 2 4 7 7
20 0 2 2 3 3 3 5
Sorted data in Array B

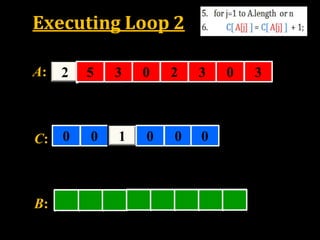
29. Time Complexity Analysis
[Loop 1]
[Loop 2]
[Loop 3]
[Loop 4]
1. Counting-Sort(A, B, k)
2. Let C[0…..k] be a new array
3.for i=0 to k
4. C[i]= 0;
5. for j=1 to A.length or n
6. C[ A[j] ] = C[ A[j] ] + 1;
7. for i=1 to k
8. C[i] = C[i] + C[i-1];
9. for j=n or A.length down to 1
10. B[ C[ A[j] ] ] = A[j];
11. C[ A[j] ] = C[ A[j] ] - 1;
Loop 2 and 4
takes O(n) time
Loop 1 and 3
takes O(k) time

30. Time Complexity Analysis
• So the counting sort takes a total time of: O(n + k)
• Counting sort is called stable sort.
– A sorting algorithm is stable when numbers with
the same values appear in the output array in the
same order as they do in the input array.

31. Counting Sort Review
•
•
•
•
Assumption: input taken from small set of numbers of size k
Basic idea:
– Count number of elements less than you for each element.
– This gives the position of that number – similar to selection
sort.
Pro’s:
– Fast
– Asymptotically fast - O(n+k)
–Simple to code
Con’s:
– Doesn’t sort in place.
– Requires O(n+k) extra storage.

32. Thank You
•
•
•
•