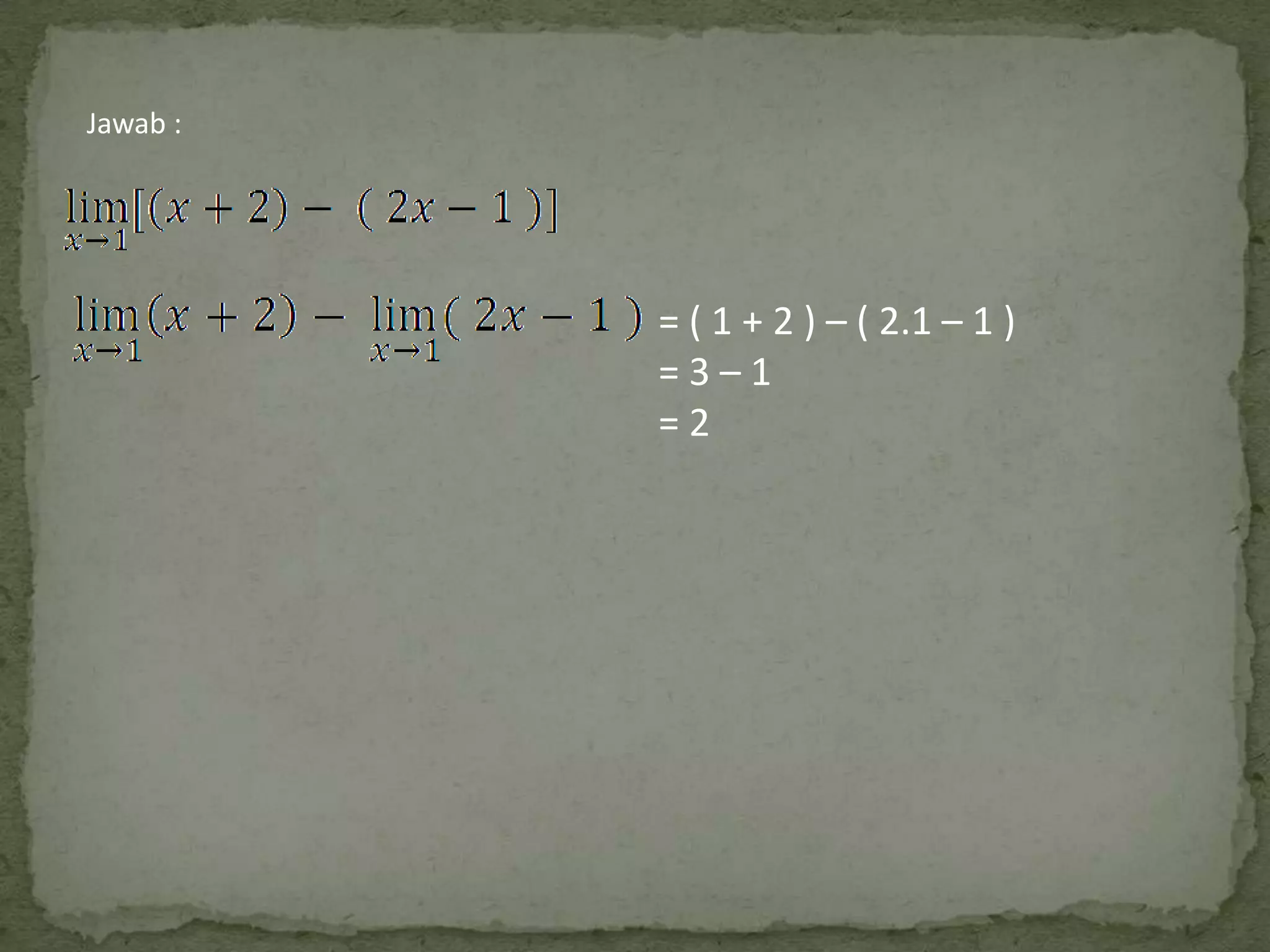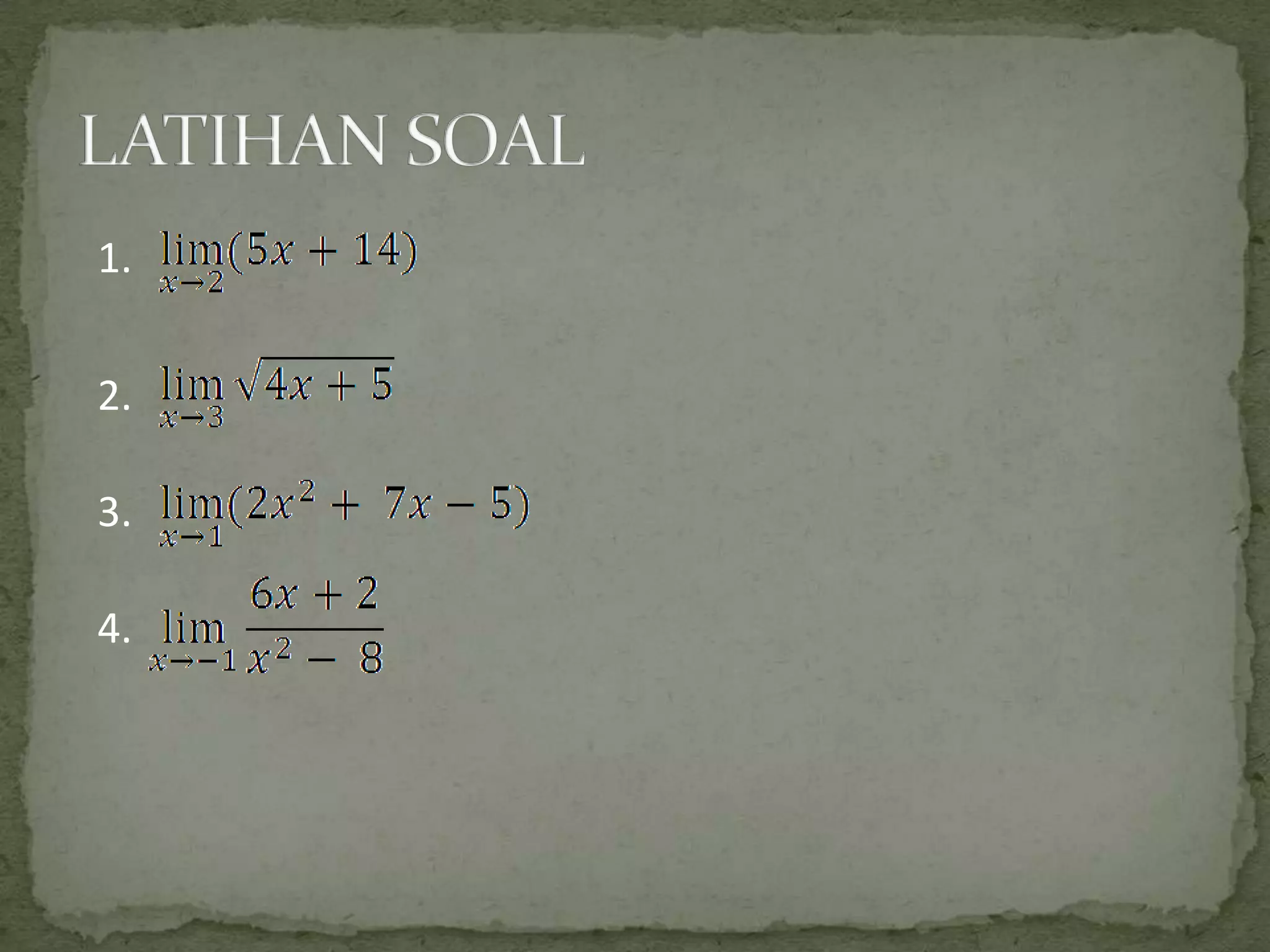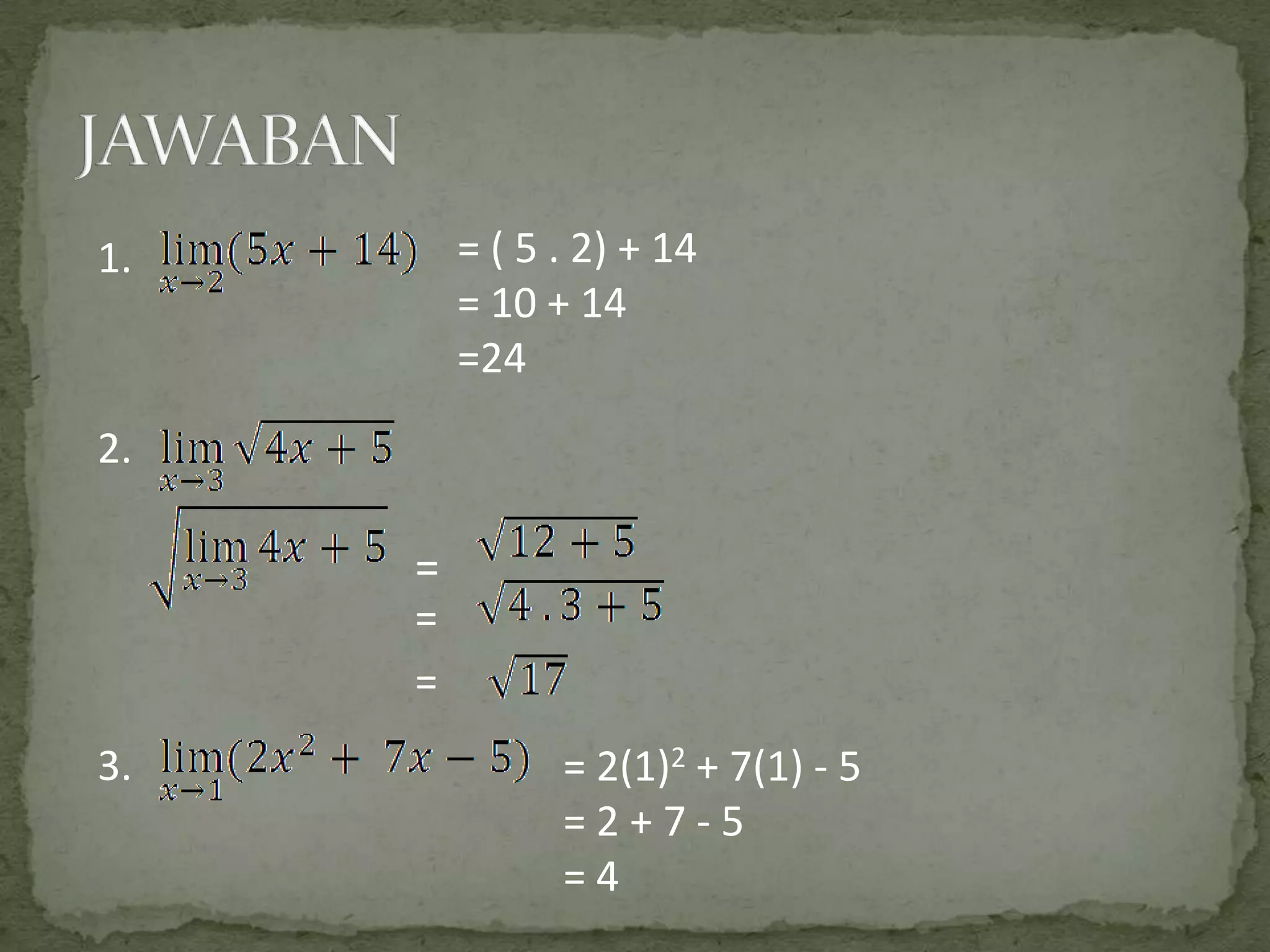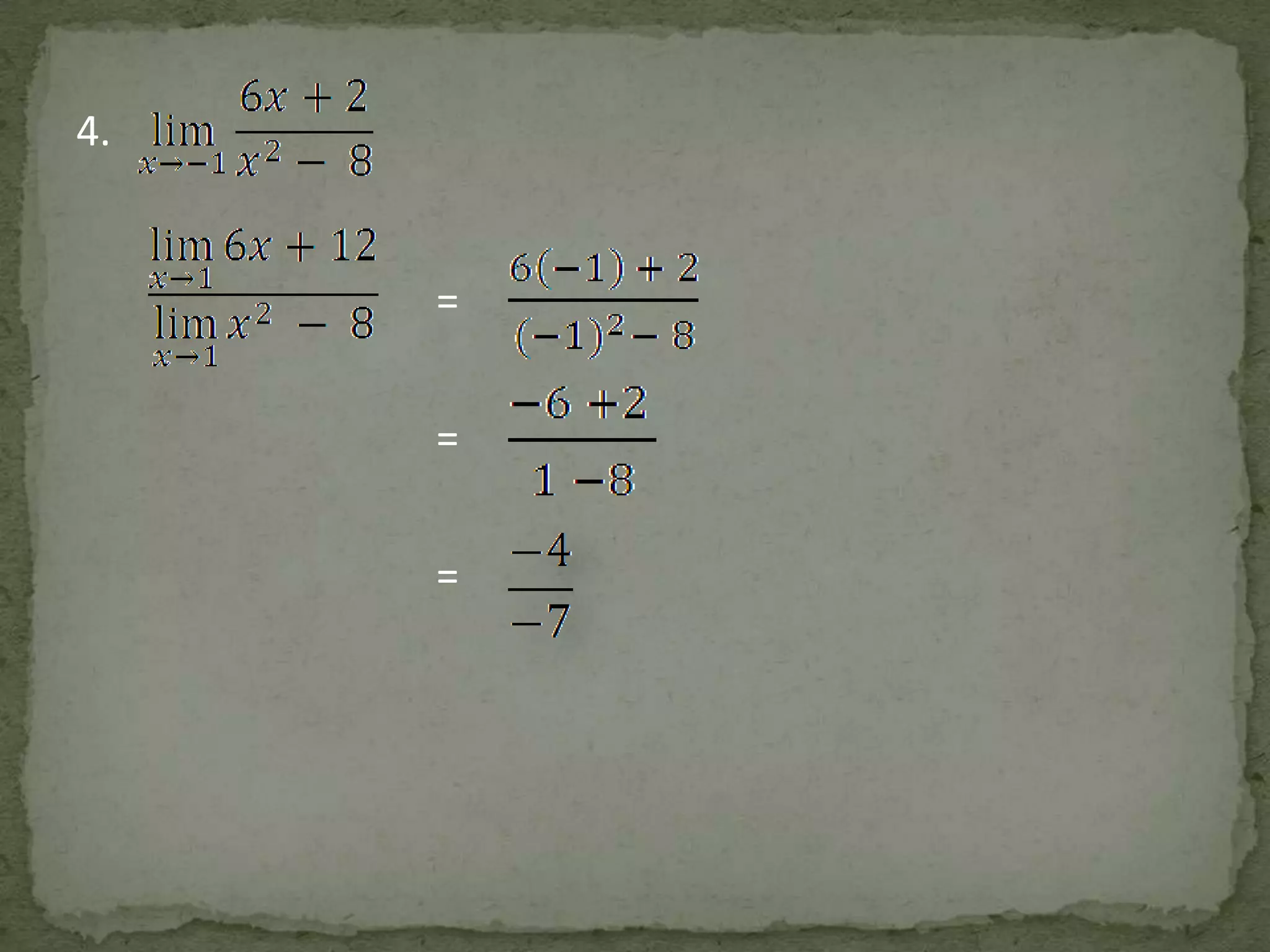Dokumen ini membahas teorema limit dalam menghitung limit fungsi dengan menyederhanakan rumus-rumus yang kompleks. Terdapat delapan sifat limit yang dijelaskan dengan contoh-contoh yang konkret. Tujuan dari dokumen ini adalah memberikan pemahaman yang lebih jelas mengenai cara menghitung limit di suatu titik.

1. OM SWASTYASTU

2. Nama Kelompok :
1. Putri Widya Arsani Silvia (31)
2.Riska Prasetyo Utami
(32)
3.Saniska Widayanti
(33)
4.Sugi Almantara
(34)
5.Sukrianingsih
(35)
6.Teresa Giovana
(36)

3. TEOREMA LIMIT

4. Menghitung limit fungsi di suatu titik
dengan menggunakan definisi dan
pembuktian seperti yang telah diuraikan
sebelumnya adalah pekerjaan rumit.
Semakin rumit bentuk fungsinya, semakin
rumit pula masalah yang dihadapi. Untuk
itu berikut ini diberikan suatu rangkaian
rumus-rumus menghitung limit di suatu
titik dengan cara sederhana.

5. Sifat Pertama
1.
Jika limit sebuah konstanta, untuk x mendekati a maka hasilnya adalah
konstanta itu sendiri.
Contoh Pertama:
1.
Jadi
Contoh Kedua:
2.
Jadi

6. Sifat Kedua
2.
Jika limit sebuah variabel, untuk x mendekati a maka hasilnya mendekati a.
Contoh :
1.
2.
Jadi
Jadi

7. Sifat Ketiga
3.
Jika limit sebuah konstanta dikali sebuah fungsi f(x) untuk x mendekati a,
maka sama dengan sebuah konstanta dikali limit sebuah fungsi f(x) untuk x mendekati a.
Contoh :
a.
Jawab
5
= 5.(2.2+2)
= 5(4+2)
= 5(6)
= 30

8. b.
Jawab
= 4 (2)
=8
Jadi hasilnya
mendekati 8

9. Sifat Keempat
4.
Jika limit sebuah fungsi f(x) ditambah fungsi g(x) , untuk x mendekati a,
maka sama dengan limit fungsi f(x) untuk x mendekati a ditambah limit fungsi g(x)
untuk x mendekati a.
Contoh:
Dit:
f(x) = x+2
g(x) = 2x-1

10. Jawab
= (1+2) + ( 2 . 1 – 1)
Jadi hasil
= 3+1
=4

11. Sifat Kelima
5.
Jika limit sebuah fungsi f(x) dikurang fungsi g(x), untuk x mendekati a,
maka sama dengan limit fungsi f(x) untuk x mendekati a dikurang limit
fungsi g(x) untuk x mendekati a .
Contoh :
5) f(x) = x +2 , g(x) = 2x-1

12. Jawab :
= ( 1 + 2 ) – ( 2.1 – 1 )
=3–1
=2

13. Sifat Keenam
6.
Jika limit sebuah fungsi f(x) dibagi dengan fungsi g(x) untuk x mendekati a sama dengan
limit sebuah fungsi f(x) untuk x mendekati a dibagi limit sebuah fungsi g(x)
untuk x mendekati a.
Contoh
f(x) =
-1
g(x) =
-1

14. =
=
=

15. ᶰ
Sifat Ketujuh
7.
Jika limit
, untuk x mendekati a, sama dengan
Contoh :
= 7 (3)²
= 7 (9)
= 63

16. Sifat Kedelapan
8.
untuk x mendekati a sama dengan
Contoh
=
=
=

17. 1.
2.
3.
4.

18. = ( 5 . 2) + 14
= 10 + 14
=24
1.
2.
=
=
=
3.
= 2(1)2 + 7(1) - 5
=2+7-5
=4

19. 4.
=
=
=