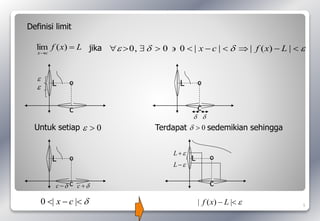
Dokumen ini membahas konsep limit dan kekontinuan dalam fungsi matematis, termasuk definisi limit, cara menghitung limit di titik tertentu, serta membedakan limit kiri dan kanan. Contoh-contoh yang diberikan menunjukkan bagaimana limit dapat dihitung dalam berbagai kondisi, termasuk limit terhadap tak hingga. Selain itu, terdapat penjelasan mengenai sifat-sifat limit pada fungsi trigonometri dan limit yang tidak ada.

1. 3. LIMIT DAN KEKONTINUAN
1

2. 1
1
)
(
2



x
x
x
f
2
3.1 Limit Fungsi di Satu Titik
Pengertian limit secara intuisi
Perhatikan fungsi
Fungsi diatas tidak terdefinisi di x=1, karena di titik tersebut f(x) berbentuk
0/0. Tapi masih bisa ditanyakan berapa nilai f(x) jika x mendekati 1
Dengan bantuan kalkulator dapat diperoleh nilai f(x) bila x mendekati 1,
seperti pada tabel berikut
x
f(x)
0.9 0.99 0.999 1.1
1.01
1.001
0.9999 1.0001
1
2
1.9 1.99 1.999 1.9999 2.0001 2.001 2.01 2.1

3. 3
1
º
2
x x
f(x)
f(x)
Secara grafik
Dari tabel dan grafik disamping
terlihat bahwa f(x) mendekati 2
jika x mendekati 1
Secara matematis dapat dituliskan
Sebagai berikut
2
1
1
lim
2
1



 x
x
x
Dibaca “ limit dari untuk x mendekati
1 adalah 2 1
1
2


x
x
Definisi(limit secara intuisi). Untuk mengatakan bahwa berarti
bahwa
L
x
f
c
x


)
(
lim
bilamana x dekat, tetapi berlainan dengan c, maka f(x) dekat ke L

4. 2
)
2
)(
1
2
(
lim
2
2
3
2
lim
2
2
2 







 x
x
x
x
x
x
x
x
5
1
2
lim
2




x
x
3
3
3
9
lim
3
9
lim
9
9









x
x
x
x
x
x
x
x
9
)
3
)(
9
(
lim
9 



 x
x
x
x
4
8
5
3
lim
1



x
x
Contoh
1.
2.
6
3
lim
9




x
x
3.
4. )
/
1
sin(
lim
0
x
x
Ambil nilai x yang mendekati 0, seperti pada tabel berikut
x
)
/
1
sin( x

/
2 
2
/
2 
3
/
2 
4
/
2 
5
/
2 
6
/
2 
7
/
2 
8
/
2
1 0 -1 0 1 0 -1 0
0
?
Dari tabel terlihat bahwa bila x menuju 0, sin(1/x) tidak menuju ke
satu nilai tertentu sehingga limitnya tidak ada

5. 5
L
x
f
c
x


)
(
lim 


 









 |
)
(
|
|
|
0
0
,
0 L
x
f
c
x
Definisi limit
jika
c
º
Untuk setiap 0


L


c
º
L


L


L
 
Terdapat sedemikian sehingga
0


c
º
L



 |
|
0 c
x 

 |
)
(
| L
x
f


c 

c c
º
L

6. )
(
lim x
f
c
x 

L
x
f
L
x
f
L
x
f
c
x
c
x
c
x



 




)
(
lim
dan
)
(
lim
)
(
lim
6
Limit Kiri dan Limit Kanan
c
x
Jika x menuju c dari arah kiri (dari arah
bilangan yang lebih kecil dari c, limit disebut
limit kiri,
)
(
lim x
f
c
x 

Jika x menuju c dari arah kanan (dari arah
bilangan yang lebih besar dari c, limit disebut
limit kanan,
c x
Hubungan antara limit dengan limit sepihak(kiri/kanan)
notasi
notasi
Jika )
(
lim x
f
c
x 


)
(
lim x
f
c
x 

maka tidak ada
)
(
lim x
f
c
x

7. )
(
lim
1
x
f
x
)
(
lim
2
x
f
x
7











1
,
2
1
0
,
0
,
)
(
2
2
x
x
x
x
x
x
x
f
)
(
lim
0
x
f
x
Contoh Diketahui
a. Hitung
d. Gambarkan grafik f(x)
Jawab
a. Karena aturan fungsi berubah di x=0, maka perlu dicari limit
kiri dan limit kanan di x=0
c. Hitung
b. Hitung Jika ada
1.

8. 0
)
(
lim
0


x
f
x
)
(
lim
2
x
f
x
8
)
(
lim
0
x
f
x 

0
lim 2
0

 

x
x
)
(
lim
0
x
f
x 

0
lim
0

 

x
x
b. Karena aturan fungsi berubah di x=1, maka perlu dicari limit
kiri dan limit kanan di x=1
)
(
lim
1
x
f
x 

1
lim
1

 

x
x
)
(
lim
1
x
f
x 

3
2
lim 2
1


 

x
x
)
(
lim
)
(
lim
1
1
x
f
x
f
x
x 



 )
(
lim
1
x
f
x
6
2
lim 2
2




x
x
Karena Tidak ada
c. Karena aturan fungsi tidak berubah di x=2, maka tidak perlu dicari limit
kiri dan limit kanan di x=2

9. 2
2
)
( x
x
f 

9
Untuk x 0

2
)
( x
x
f 
Grafik: parabola
Untuk 0<x<1
f(x)=x
Grafik:garis lurus
Untuk x 1

Grafik: parabola
1
3
º
di x=1 limit tidak
ada
Grafik f(x)

10. 10
2. Tentukan konstanta c agar fungsi










1
,
1
,
3
)
( 2
x
c
x
x
cx
x
f
mempunyai limit di x=-1
Jawab
Agar f(x) mempunyai limit di x=-1, maka limit kiri harus sama dengan
limit kanan
)
(
lim
1
x
f
x 


c
cx
x



 


3
3
lim
1
)
(
lim
1
x
f
x 


c
c
x
x



 


1
lim 2
1
Agar limit ada 3+ c=1-c
C=-1

11. 11
)
(
lim
3
x
f
x 

)
(
lim
1
x
f
x 

)
(
lim
1
x
f
x
)
(
lim
1
x
f
x 

)
(
lim
1
x
f
x 

A. Diberikan grafik suatu fungsi f seperti gambar berikut .
Cari limit /nilai fungsi berikut, atau nyatakan bahwa limit /nilai
fungsi tidak ada.
f(-3)
f(-1)
f(1)
1.
2.
3.
4.
5.
6.
7.
8.
Soal Latihan

12.   LG
x
g
x
f
x
g
x
f
a
x
a
x
a
x





)
(
lim
)
(
lim
)
(
)
(
lim
0
,
)
(
lim
)
(
lim
)
(
)
(
lim 





G
bila
G
L
x
g
x
f
x
g
x
f
a
x
a
x
a
x
n
n
a
x
n
a
x
L
x
f
x
f 



)
(
lim
)
(
lim
12
G
x
g
L
x
f
a
x
a
x




)
(
lim
dan
)
(
lim
  G
L
x
g
x
f
x
g
x
f
a
x
a
x
a
x








)
(
lim
)
(
lim
)
(
)
(
lim
Sifat limit fungsi
Misal
(limit dari f , g ada dan berhingga)
maka
2.
3.
4.
n
a
x
n
a
x
x
f
x
f ))
(
lim
(
))
(
(
lim


 ,n bilangan bulat positif
5. bila n genap L harus positif
1.

13. 2
2
2
)
1
(
1
1
sin
)
1
(
)
1
( 





 x
x
x
x
)
(
)
(
)
( x
h
x
g
x
f 

0
1
1
sin
)
1
(
lim 2
1



 x
x
x 13
L
x
h
L
x
f
c
x
c
x




)
(
lim
serta
)
(
lim
L
x
g
c
x


)
(
lim
1
1
sin
)
1
(
lim 2
1 

 x
x
x
Prinsip Apit
Misal untuk x disekitar c dan
maka
Contoh Hitung
Karena 1
)
1
1
sin(
1 



x
dan
0
)
1
(
lim 2
1




x
x
0
)
1
(
lim
, 2
1



x
x
maka

14. 14
Limit Fungsi Trigonometri
1
sin
lim
.
1
0

 x
x
x
1
cos
lim
.
2
0


x
x
1
tan
lim
.
3
0

 x
x
x
Contoh
2
.
2
2
tan
5
4
.
4
4
sin
3
lim
2
tan
5
4
sin
3
lim
0
0
x
x
x
x
x
x
x
x
x
x







2
.
2
2
tan
lim
5
4
.
4
4
sin
lim
3
0
0
x
x
x
x
x
x





3
7
2
.
2
2
tan
lim
5
4
.
4
4
sin
lim
3
0
2
0
4






x
x
x
x
x
x
x  0 ekivalen dgn 4x  0

15. atas
arah
dari
0
)
(
dan
0
jika
,
)
( 


 x
g
L
i
15
Limit Tak Hingga dan Limit di Tak Hingga
Limit Tak Hingga
maka
,
0
)
(
lim
dan
0
)
(
lim
Misal 




x
g
L
x
f
a
x
a
x

 )
(
)
(
lim
x
g
x
f
a
x
bawah
arah
dari
0
)
(
dan
0
jika
,
)
( 


 x
g
L
ii
bawah
arah
dari
0
)
(
dan
0
jika
,
)
( 


 x
g
L
iii
atas
arah
dari
0
)
(
dan
0
jika
,
)
( 


 x
g
L
iv
Ctt : g(x)  0 dari arah atas maksudnya g(x) menuju 0 dari nilai g(x)
positif.
g(x)  0 dari arah bawah maksudnya g(x) menuju 0 dari nilai g(x)
negatif.

16. 0
2
1
lim 2
1






x
x






 1
1
lim 2
2
1 x
x
x
16
Contoh Hitung
1
1
lim
2
1 


 x
x
x
a.
1
1
lim 2
2
1 



 x
x
x
b.
Jawab
a. 0
2
1
lim 2
1





x
x
,g(x)=x-1 akan menuju 0 dari arah bawah, karena
x  1 dari kiri berarti x lebih kecil dari 1, akibatnya
x-1 akan bernilai negatif
Sehingga





 1
1
lim
2
1 x
x
x
b. akan menuju 0 dari arah atas, karena
x  -1 dari kiri berarti x lebih kecil dari -1, tapi
bilangan negatif yang lebih kecil dari -1 jika dikuadrat
kan lebih besar dari 1 sehingga bernilai positif
1
)
( 2

 x
x
g
1
2

x
Sehingga

17. L
x
f
x



)
(
lim
17
Limit di Tak Hingga
a. jika 
 







 |
)
(
|
0
0 L
x
f
M
x
M
atau f(x) mendekati L jika x menuju tak hingga
L
x
Contoh Hitung
4
2
5
2
lim 2
2




 x
x
x
x
Jawab
)
2
(
)
1
(
lim
2
2
4
2
5
2
2
x
x
x
x x
x






4
2
5
2
lim 2
2




 x
x
x
x
2
2
4
2
5
2
1
lim
x
x
x
x






= 1/2

18. 18
L
x
f
x



)
(
lim jika 
 







 |
)
(
|
0
0 L
x
f
M
x
M
atau f(x) mendekati L jika x menuju minus tak hingga
b.
L
x
Contoh Hitung
4
2
5
2
lim 2



 x
x
x
4
2
5
2
lim 2



 x
x
x
Jawab
)
2
(
)
(
lim
2
2
4
2
5
2
2
x
x
x
x x
x





)
2
(
)
(
lim
2
2
4
5
2
x
x
x
x 




= 0

19.  


x
x
x
x





3
lim 2
)
3
3
(
3
lim
2
2
2
x
x
x
x
x
x
x
x
x
x












19
Contoh Hitung
x
x
x
x





3
lim 2
Jawab :
Jika x  , limit diatas adalah bentuk ( )
x
x
x
x
x
x
x









3
3
lim
2
2
2
x
x
x
x
x







3
3
lim
2
x
x
x
x
x
x
x







)
1
(
)
1
(
lim
2
3
1
2
3
|
|
2
x
x 
x
x
x
x
x
x
x 







2
3
1
3
1
)
1
(
lim
2
1
)
1
1
(
1
lim
2
3
1
3










x
x
x
x

20. ada
)
(
lim x
f
a
x
)
(
)
(
lim a
f
x
f
a
x


20
Kekontinuan Fungsi
Fungsi f(x) dikatakan kontinu pada suatu titik x = a jika
(i) f(a) ada
(ii)
(iii)
Jika paling kurang salah satu syarat diatas tidak dipenuhi maka f dikatakan
tidak kontinu di x=a
a
(i)
º
f(a) tidak ada
f tidak kontinu di x=a

21. 21
a
(ii)
1
L
2
L
Karena limit kiri(L1) tidak
sama dengan limit kanan(L2)
maka f(x) tidak mempunyai limit
di x=a
Fungsi f(x) tidak kontinu di x=a
(iii)
a
●
º
f(a)
f(a) ada
)
(
lim x
f
a
x
L ada
Tapi nilai fungsi tidak sama dengan
limit fungsi
Fungsi f(x) tidak kontinu di x=a

22. 22
(iv)
a
f(a)
f(a) ada
)
(
lim x
f
a
x
ada
)
(
)
(
lim a
f
x
f
a
x


f(x) kontinu di x=a
Ketakkontinuan terhapus
Ketakkontinuan kasus (i) bisa dihapus
dengan cara mendefinisikan nilai fungsi
dititik tersebut = limit fungsi
a
º

23. 23
contoh
Periksa apakah fungsi berikut kontinu di x=2, jika tidak sebutkan
alasannya
2
4
)
(
2



x
x
x
f










2
,
3
2
,
2
4
)
(
2
x
x
x
x
x
f
a. b.








2
,
1
2
,
1
)
( 2
x
x
x
x
x
f
c.
Jawab :
a. Fungsi tidak terdefinisi di x=2 (bentuk 0/0) f(x) tidak kontinu
di x=2
b. - f(2) = 3
4
2
lim
)
2
(
)
2
)(
2
(
lim
2
4
lim
2
2
2
2












x
x
x
x
x
x
x
x
x
)
2
(
)
(
lim
2
f
x
f
x


-
-
Karena limit tidak sama dengan nilai fungsi, maka f(x) tidak
kontinu di x=2

24. 24
c. 3
1
2
)
2
( 2



f
-
- 3
1
lim
)
(
lim
2
2


 



x
x
f
x
x
3
1
lim
)
(
lim 2
2
2


 



x
x
f
x
x
3
)
(
lim
2


x
f
x
)
2
(
)
(
lim
2
f
x
f
x


-
Karena semua syarat dipenuhi  f(x) kontinu di x=2

25. 25
Kontinu kiri dan kontinu kanan
Fungsi f(x) disebut kontinu kiri di x=a jika
)
(
)
(
lim a
f
x
f
a
x



Fungsi f(x) disebut kontinu kanan di x=a jika
)
(
)
(
lim a
f
x
f
a
x



Fungsi f(x) kontinu di x=a jika kontinu kiri dan kontinu kanan di x=a
Contoh : Tentukan konstanta a agar fungsi








2
,
1
2
,
)
( 2
x
ax
x
a
x
x
f
Kontinu di x=2

26. )
2
(
)
(
lim
2
f
x
f
x



1
4
1
2
)
2
( 2



 a
a
f
26
Jawab :
Agar f(x) kontinu di x=2, haruslah
f kontinu kiri di x=2
)
2
(
)
(
lim
2
f
x
f
x



a
a
x
x
f
x
x



 



2
lim
)
(
lim
2
2
1
4
1
2
)
2
( 2



 a
a
f
2 + a = 4a – 1
-3a = -3
a = 1
f kontinu kanan di x=2
1
4
1
lim
)
(
lim 2
2
2



 



a
ax
x
f
x
x
Selalu
dipenuhi

27. 27
1. Diketahui










1
,
2
2
1
,
1
)
(
2
x
x
x
x
x
f
selidiki kekontinuan fungsi f(x) di x = -1
Soal Latihan
2. Agar fungsi












2
,
3
2
1
,
1
,
1
)
(
x
x
x
b
ax
x
x
x
f
kontinu pada R, maka berapakah a + 2b ?
3. Tentukan a dan b agar fungsi












2
,
4
2
2
,
2
4
)
(
2
x
x
x
x
bx
ax
x
f
kontinu di x = 2

28. Kekontinuan pada interval
 Fungsi f(x) dikatakan kontinu pada interval buka ( a,b ) bila
f(x) kontinu pada setiap titik di dalam interval tersebut.
 Sedangkan f(x) dikatakan kontinu pada interval tutup [ a,b ]
bila :
28
1. f(x) kontinu pada ( a,b )
2. f(x) kontinu kanan di x = a
3. f(x) kontinu kiri di x = b
Bila f(x) kontinu untuk setiap nilai x  R maka dikatakan
f(x) kontinu ( dimana-mana ).

29.  Teorema 3.2
 Fungsi Polinom kontinu dimana-mana
 Fungsi Rasional kontinu pada Domainnya
 Misalkan , maka
◦ f(x) kontinu di setiap titik di R jika n ganjil
◦ f(x) kontinu di setiap R positif jika n genap.
Contoh : tentukan selang kekontinuan
Dari teorema diatas diperoleh f(x) kontinu untuk x-4>0 atau x>4.
f(x) kontinu kanan di x=4
Sehingga f(x) kontinu pada [4, )
29
n
x
x
f 
)
(
4
)
( 
 x
x
f
)
4
(
0
4
lim
)
(
lim
4
4
f
x
x
f
x
x



 





30. Limit dan Kekontinuan Fungsi Komposisi
 Teorema Limit Fungsi Komposisi:
Jika dan f(x) kontinu di L, maka
 Teorema kekontinuan fungsi komposisi:
Jika g(x) kontinu di a, f(x) kontinu di g(a), maka fungsi
kontinu di a.
Bukti
karena f kontinu di g(a)
= f(g(a)) karena g kontinu di a
= (fog)(a)
30
L
x
g
a
x


)
(
lim
)
(
))
(
lim
(
))
(
(
lim L
f
x
g
f
x
g
f
a
x
a
x




)
)(
( x
g
f 
))
(
(
lim
)
)(
(
lim x
g
f
x
g
f
a
x
a
x 



))
(
lim
( x
g
f
a
x


31. 31













4
3
1
3
cos
)
( 2
4
x
x
x
x
x
f
)
)(
(
)
( x
h
g
x
f 

4
3
1
3
)
( 2
4





x
x
x
x
x
h dan g(x) = cos x
Contoh Tentukan dimana fungsi
kontinu
Jawab :
Fungsi f(x) dapat dituliskan sebagai komposisi dua fungsi atau
dengan
Karena h(x) kontinu di R-{-4,1} dan g(x) kontinu dimana-mana maka
fungsi f(x) kontinu di R-{-4,1}