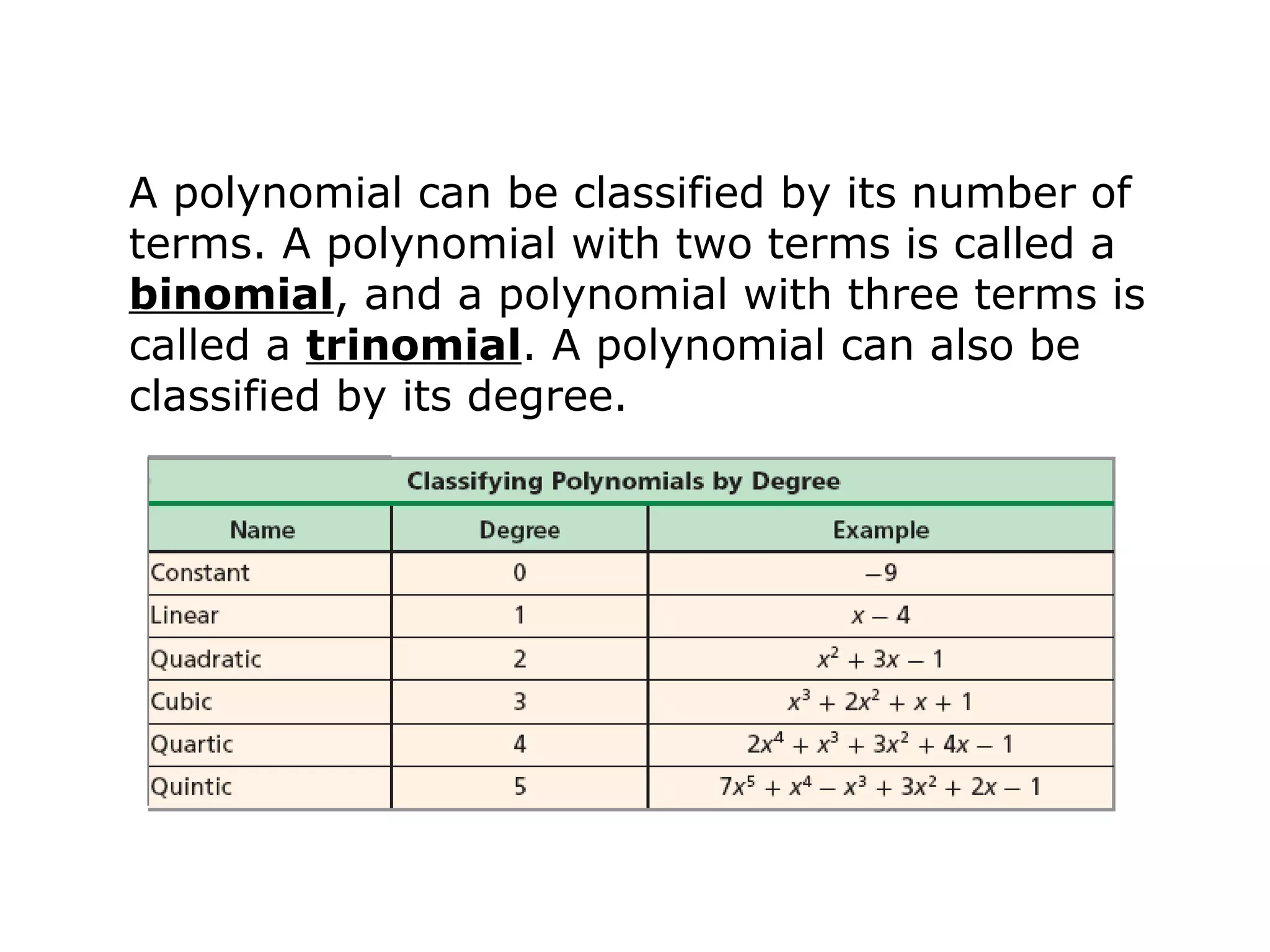
The document discusses polynomials. It defines a monomial as a number or product of numbers and variables with whole number exponents, and a polynomial as a sum or difference of monomials. It explains that the degree of a monomial or polynomial is determined by summing the exponents of its variables. The document provides examples of identifying the degree of monomials, classifying polynomials by their leading coefficient, degree, and number of terms, and adding or subtracting polynomials.

1. Objectives
Identify, classify, evaluate,
polynomials.
Add, and subtract polynomials.

2. A monomial is a number or a product of numbers
and variables with whole number exponents. A
polynomial is a monomial or a sum or difference of
monomials. Each monomial in a polynomial is a
term. Because a monomial has only one term, it is
the simplest type of polynomial.
Polynomials have no variables in denominators or
exponents, no roots or absolute values of variables,
and all variables have whole number exponents.
Polynomials: 3x4 2z12 + 9z3 1
2 a7 0.15x101 3t2 – t3
Not polynomials: 3x |2b3 – 6b| 8
1
2 x
5y2 m0.75 – m
The degree of a monomial is the sum of the
exponents of the variables.

3. Example 1: Identifying the Degree of a Monomial
Identify the degree of each monomial.
A. z6
z6 5.6 = 5.6x0 Identify the
Identify the
exponent.
B. 5.6
The degree is 6.
exponent.
The degree is 0.
C. 8xy3
8x1y3 a2b1c3 Add the
Add the
exponents.
D. a2bc3
The degree is 4.
exponents.
The degree is 6.

4. Check It Out! Example 1
Identify the degree of each monomial.
a. x3
x3 7 = 7x0 Identify the
Identify the
exponent.
b. 7
The degree is 3.
exponent.
The degree is 0.
c. 5x3y2
5x3y2 a6b1c2 Add the
Add the
exponents.
d. a6bc2
The degree is 5.
exponents.
The degree is 9.

5. The degree of a monomial is the sum
of the exponents of the variables.
Find the degree of each monomial.
1) 5x2
2
2) 4a4b3c
8
3) -3
0

6. An degree of a polynomial is given by the
term with the greatest degree. A polynomial with
one variable is in standard form when its terms
are written in descending order by degree. So, in
standard form, the degree of the first term
indicates the degree of the polynomial, and the
leading coefficient is the coefficient of the first
term.

7. A polynomial can be classified by its number of
terms. A polynomial with two terms is called a
binomial, and a polynomial with three terms is
called a trinomial. A polynomial can also be
classified by its degree.

8. Example 2: Classifying Polynomials
Rewrite each polynomial in standard form.
Then identify the leading coefficient, degree,
and number of terms. Name the polynomial.
A. 3 – 5x2 + 4x B. 3x2 – 4 + 8x4
Write terms in
descending order by
degree.
–5x2 + 4x + 3
Leading coefficient: –5
Degree: 2
Terms: 3
Name: quadratic trinomial
Write terms in
descending order by
degree.
8x4 + 3x2 – 4
Leading coefficient: 8
Degree: 4
Terms: 3
Name: quartic trinomial

9. State whether each
expression is a polynomial. If
it is, identify it.
1) 7y - 3x + 4
trinomial
2) 10x3yz2
monomial
3)
not a polynomial
5 7
2
2
y
y
+

10. A polynomial is normally put in
ascending or descending order.
What is ascending order?
Going from small to big exponents.
What is descending order?
Going from big to small exponents.

11. Put in descending order:
1) 8x - 3x2 + x4 - 4
x4 - 3x2 + 8x - 4
2) Put in descending order in terms of
x:
12x2y3 - 6x3y2 + 3y - 2x
-6x3y2 + 12x2y3 - 2x + 3y

12. 3) Put in ascending order in terms of
y:
12x2y3 - 6x3y2 + 3y - 2x
-2x + 3y - 6x3y2 + 12x2y3
4) Put in ascending order:
5a3 - 3 + 2a - a2
-3 + 2a - a2 + 5a3

13. Write in ascending order in terms of
y:
x4 – x3y2 + 4xy – 2x2y3
1. x4 + 4xy – x3y2– 2x2y3
2. – 2x2y3 – x3y2 + 4xy + x4
3. x4 – x3y2– 2x2y3 + 4xy
4. 4xy – 2x2y3 – x3y2 + x4

14. Example 3: Adding and Subtracting Polynomials
Add or subtract. Write your answer in
standard form.
B. (3 – 2x2) – (x2 + 6 – x)
Add the opposite horizontally.
(3 – 2x2) – (x2 + 6 – x)
Write in standard form.
Group like terms.
Add.
(–2x2 + 3) + (–x2 + x – 6)
(–2x2 – x2) + (x) + (3 – 6)
–3x2 + x – 3