This document provides information about the Laplace transform of periodic functions. It discusses the Laplace transform of periodic square waves, triangular waves, sawtooth waves, and staircase functions. It also discusses the Laplace transform of full-wave and half-wave rectification of a sine wave. Examples are provided to show how to calculate the Laplace transform of each of these periodic and rectified functions.








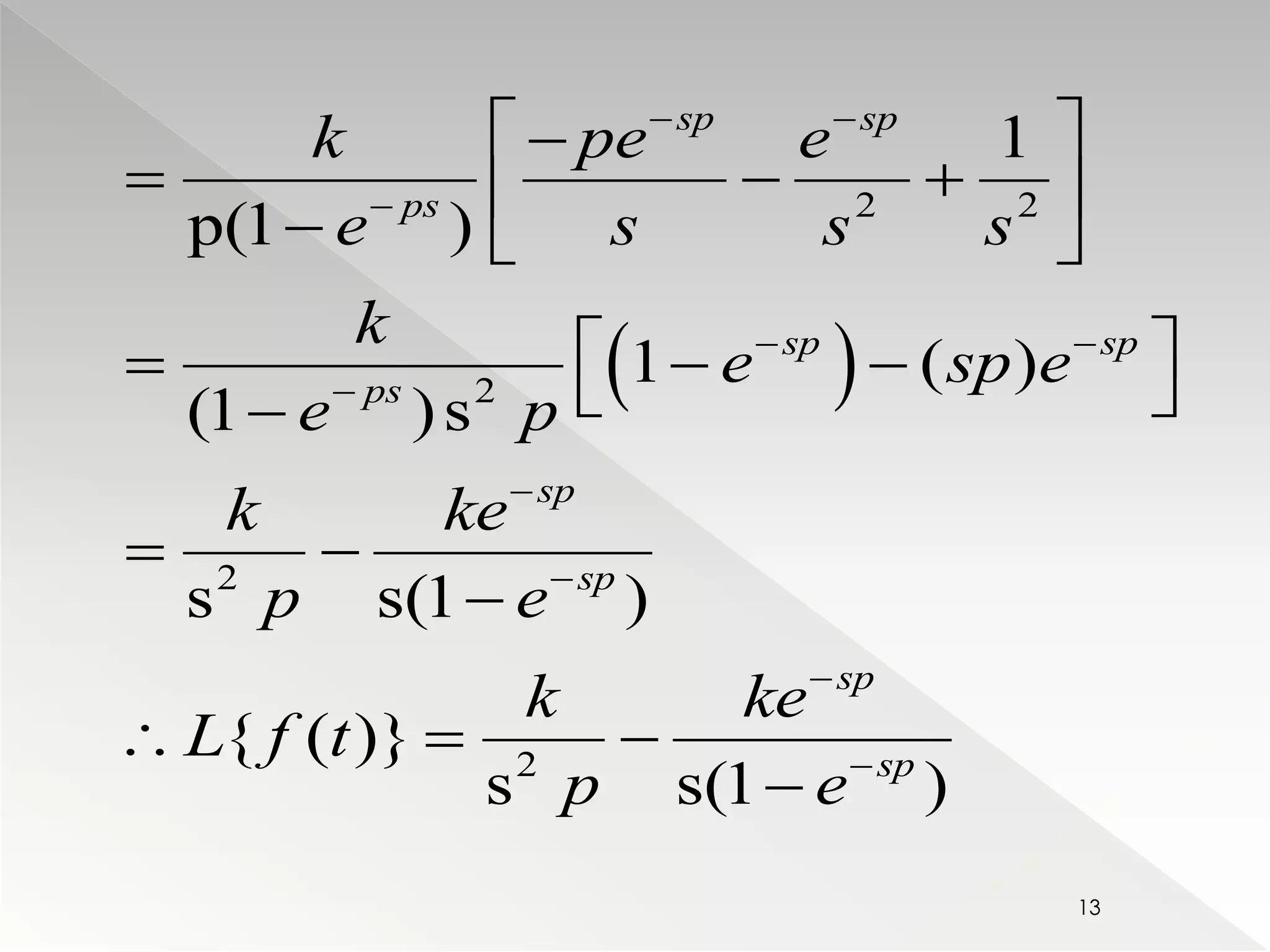


![
[g(t)] { ( )}
2 2
[g(t)]
1
[g(t)]
1
sp
sp
sp
sp
kt
L L L h t
p
k k ke
L
ps s p s e
ke
L
s e
16](https://image.slidesharecdn.com/mathesppt-141012085025-conversion-gate02/75/Laplace-periodic-function-with-graph-16-2048.jpg)

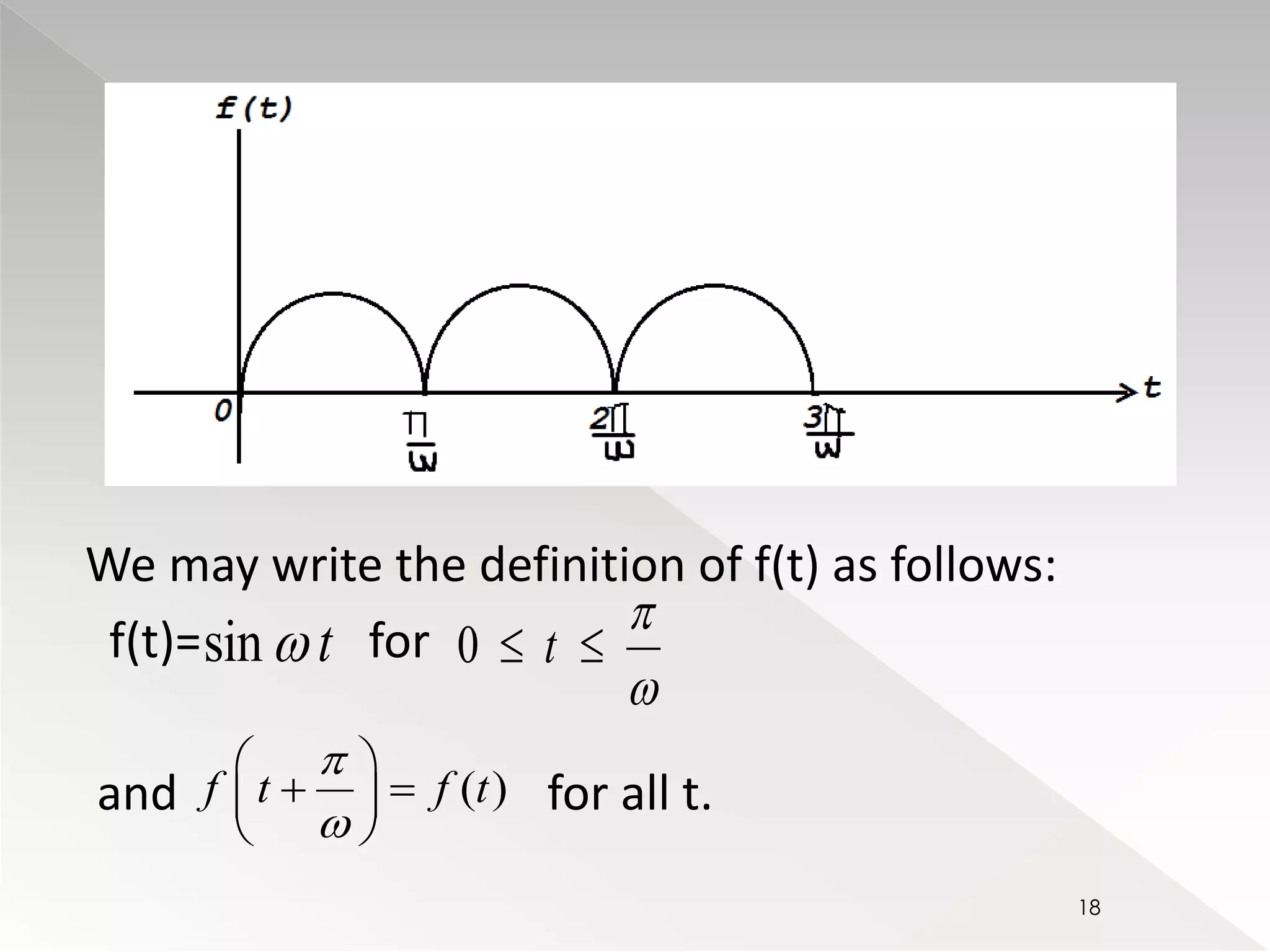
![
L f t e tdt
0
st
st
2 2
s
st
0 0
2 2
0
2 2
0
1
[ ( )] sin
1
sin ( .sin cos )
1
sin
sin 1
s
st
s
st
e
e
Now e tdt s t t
s
e tdt e
s
e tdt e
s
19](https://image.slidesharecdn.com/mathesppt-141012085025-conversion-gate02/75/Laplace-periodic-function-with-graph-19-2048.jpg)
![
L f t e
[ ( )] . 1
2 2
2
1
2 2
2
2 2
1
1
[ ( )] .
1
[ ( )] coth
2
s
s
s s
s s
s
e
e e
L f t
s
e e
s
L f t
s
20](https://image.slidesharecdn.com/mathesppt-141012085025-conversion-gate02/75/Laplace-periodic-function-with-graph-20-2048.jpg)

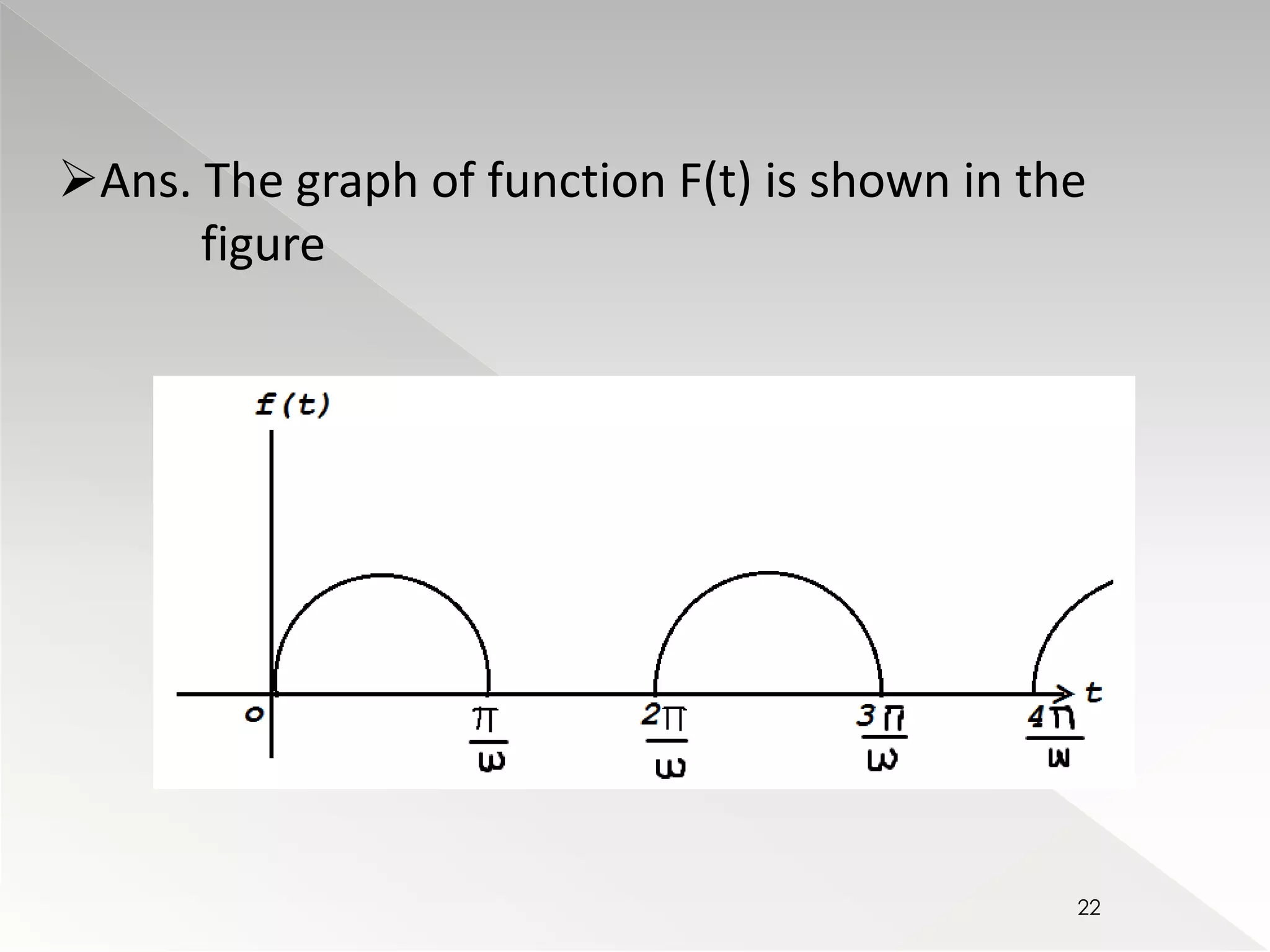
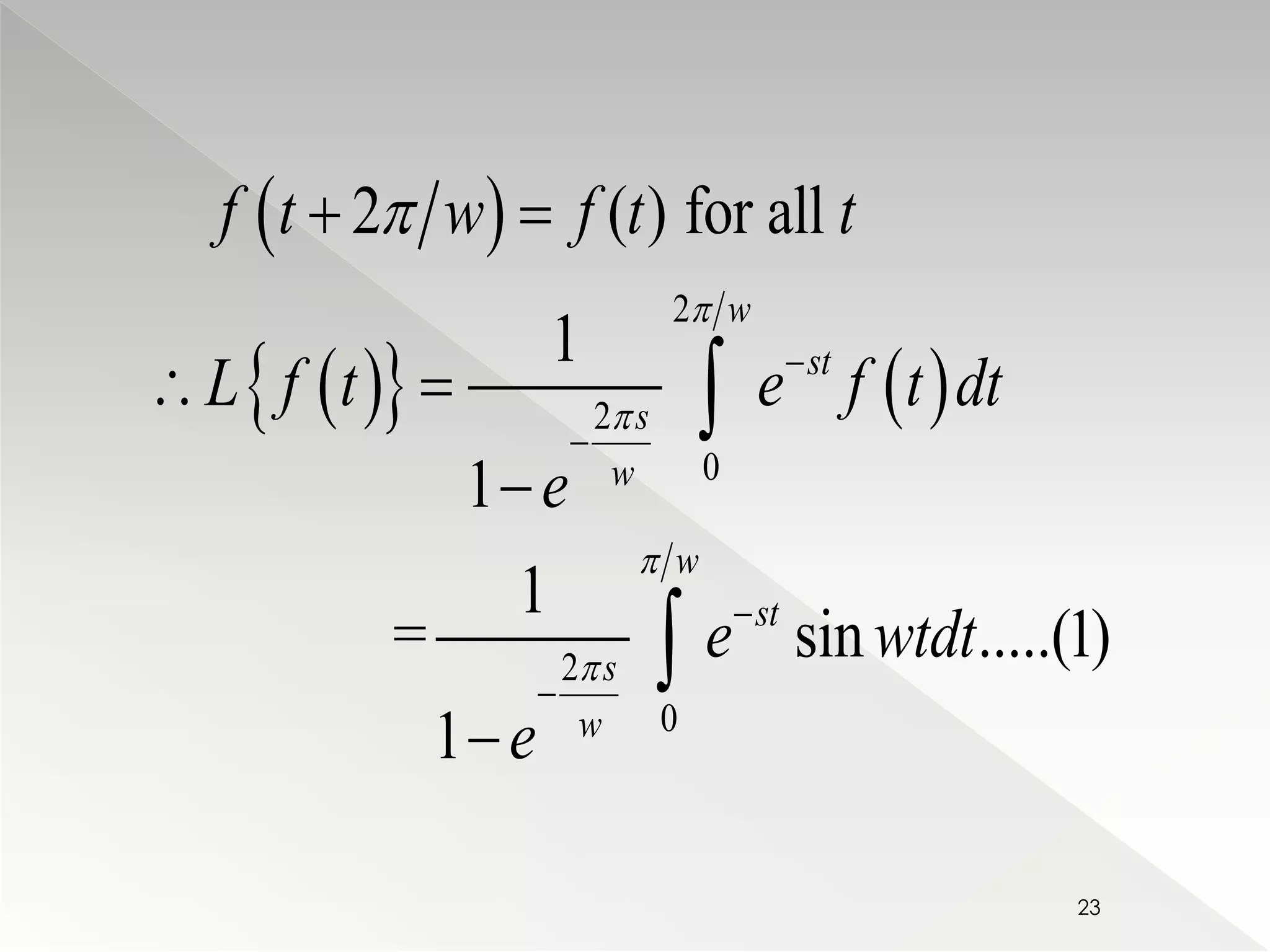







![st
s a r
( )
a
0
as sr as
0
1
(u )) ,
(r)
(r) ( )
as as
{ ( ) u(t a)} ( ) [ ( )]
[ as
( )] ( ) ( )
e f a dt Substituting t a r
e f dr
e e f dr e f s
L f t a e f s e L f t
L e
f s f t a u t a
31](https://image.slidesharecdn.com/mathesppt-141012085025-conversion-gate02/75/Laplace-periodic-function-with-graph-31-2048.jpg)
![as
Cor L f t u t a e L f t a
.1: { ( ) ( )} [ ( )]
(alternative form of second shifting theorem)
as
Cor L u t a L u t a e L
.2 : [ ( )] [1. ( )] (1)
Cor L u t a u t b
.3 : [ ( ) ( )]
as
as bs
e
s
e e
as bs
s
Cor L f t u t a u t b e L f t a e L f t b
.4 : [ ( ) { ( ) ( )] { ( )} { (
)}
32](https://image.slidesharecdn.com/mathesppt-141012085025-conversion-gate02/75/Laplace-periodic-function-with-graph-32-2048.jpg)

