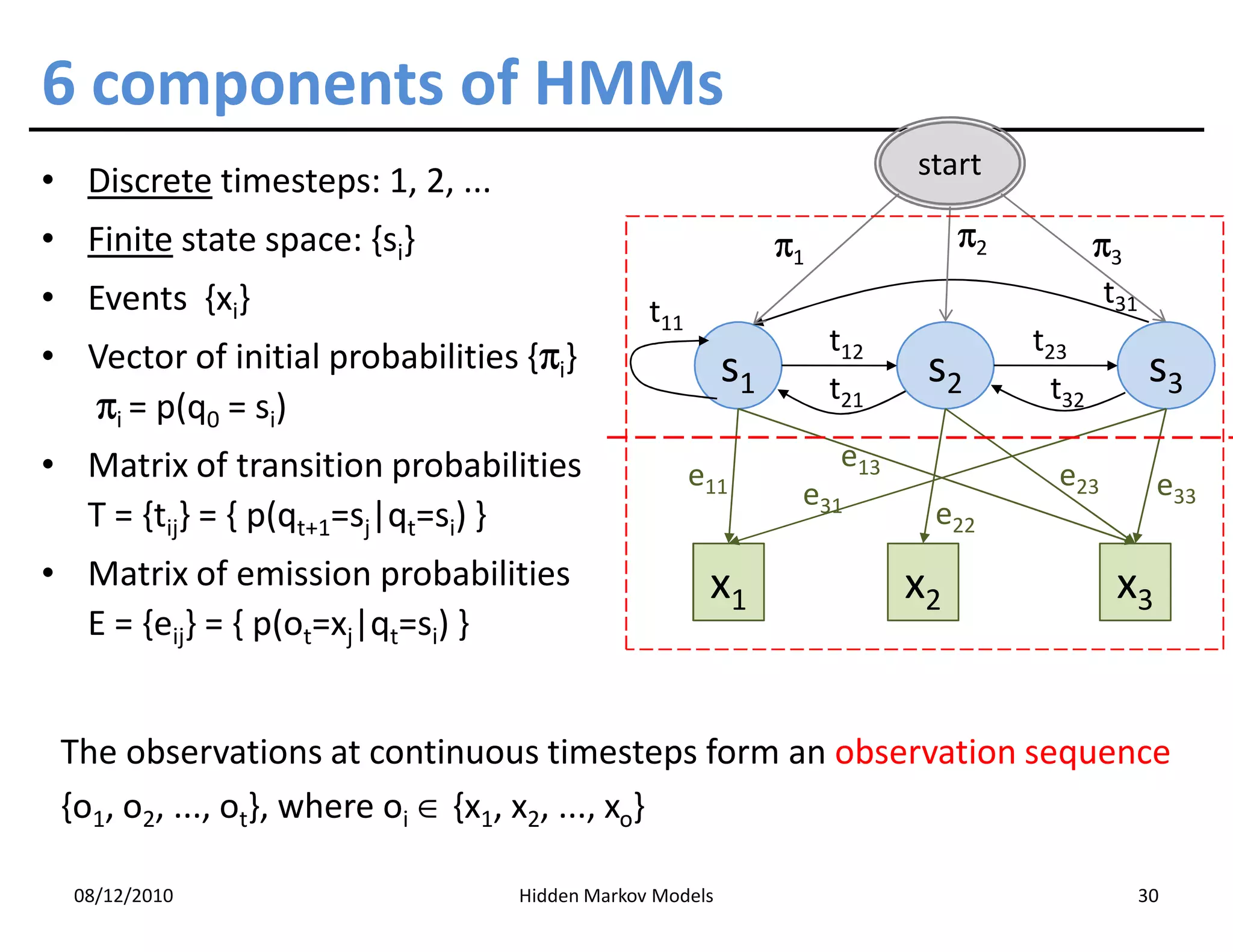
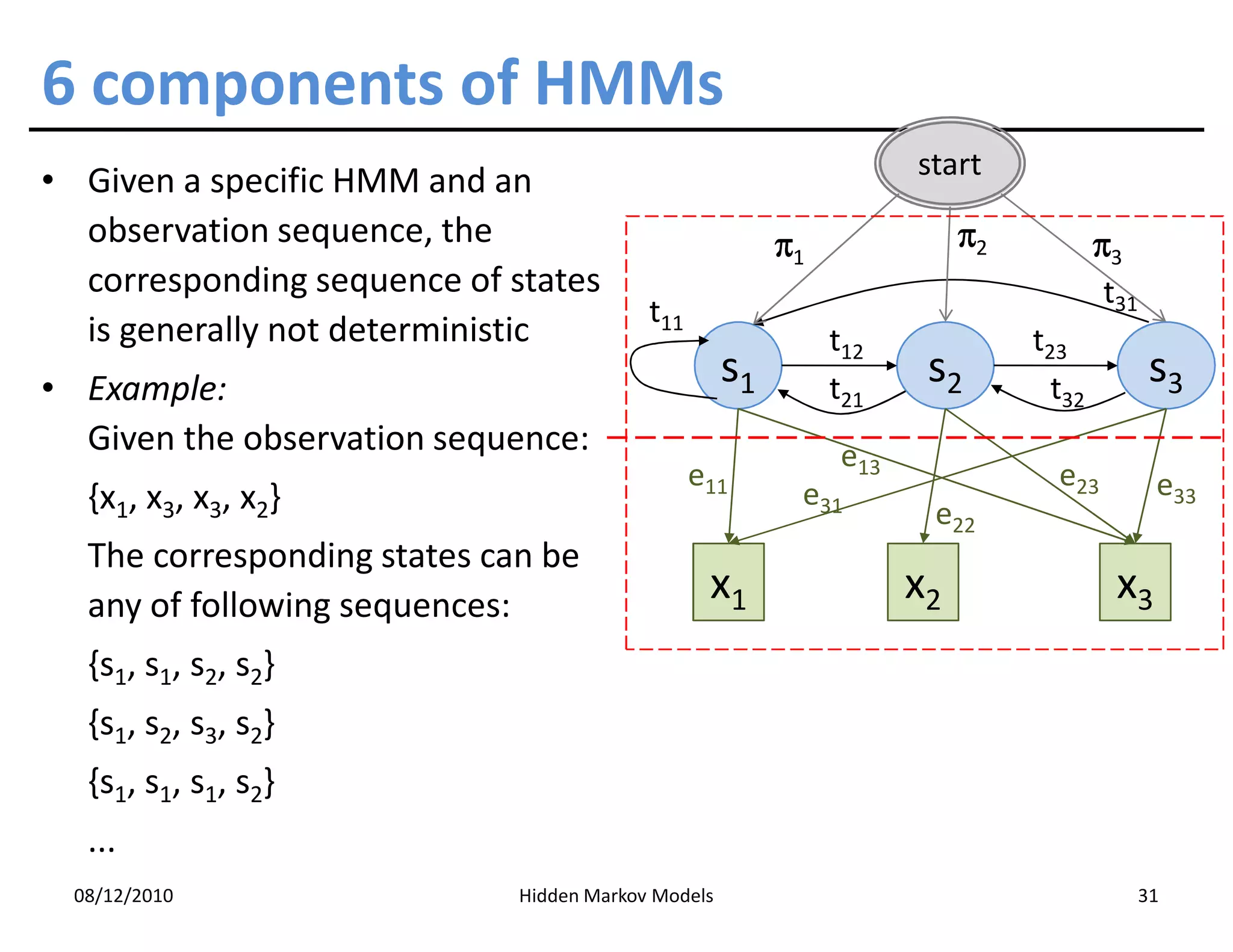
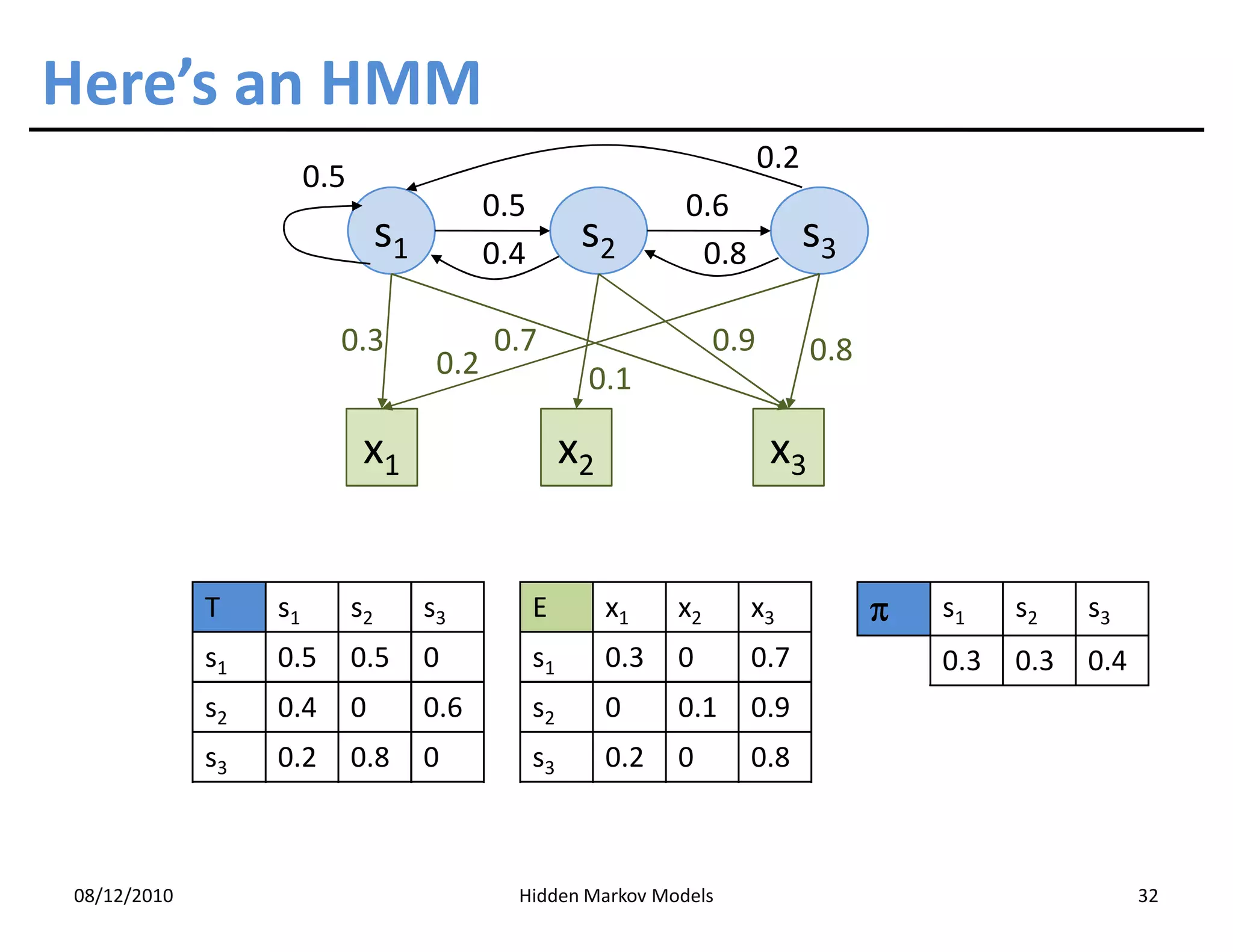
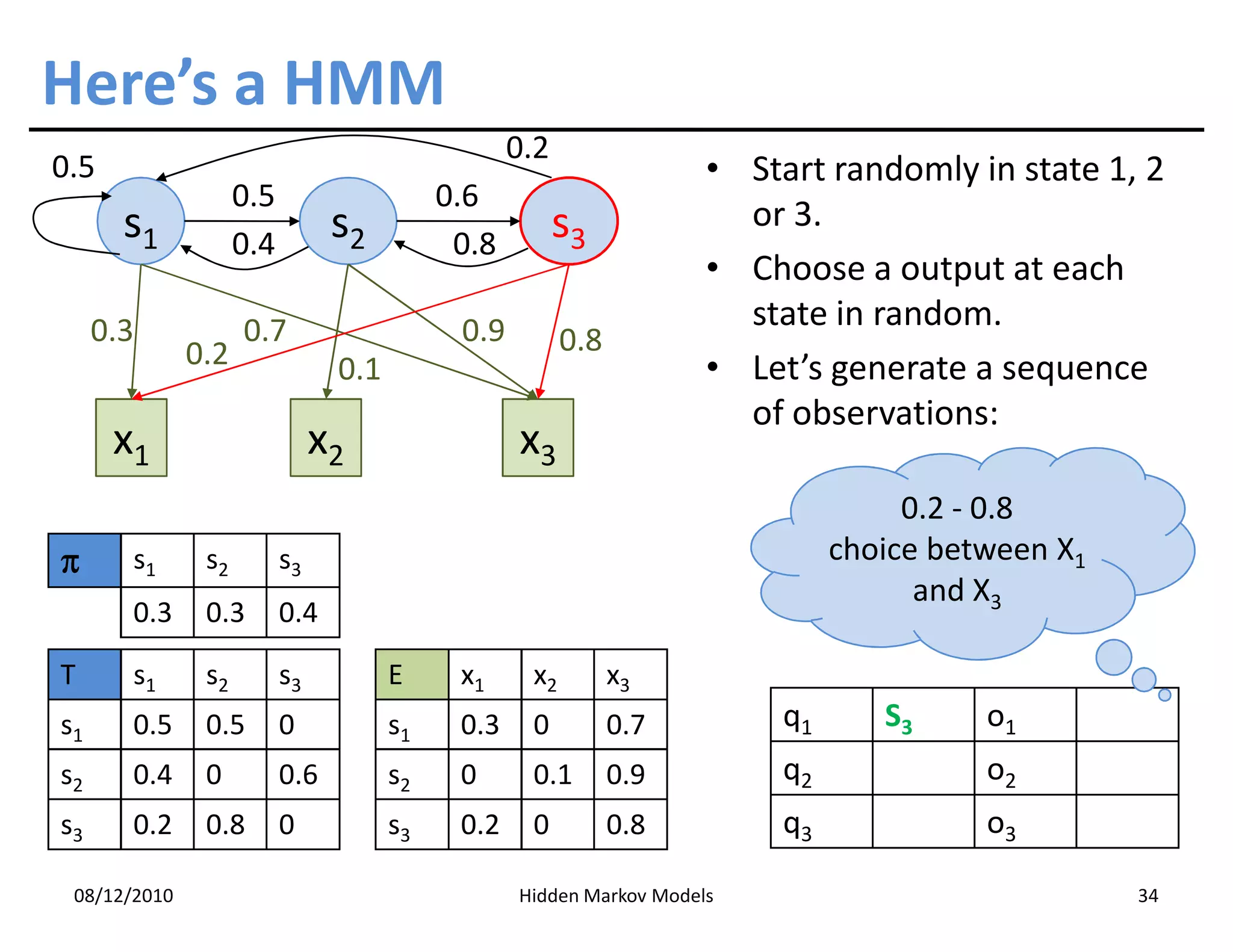
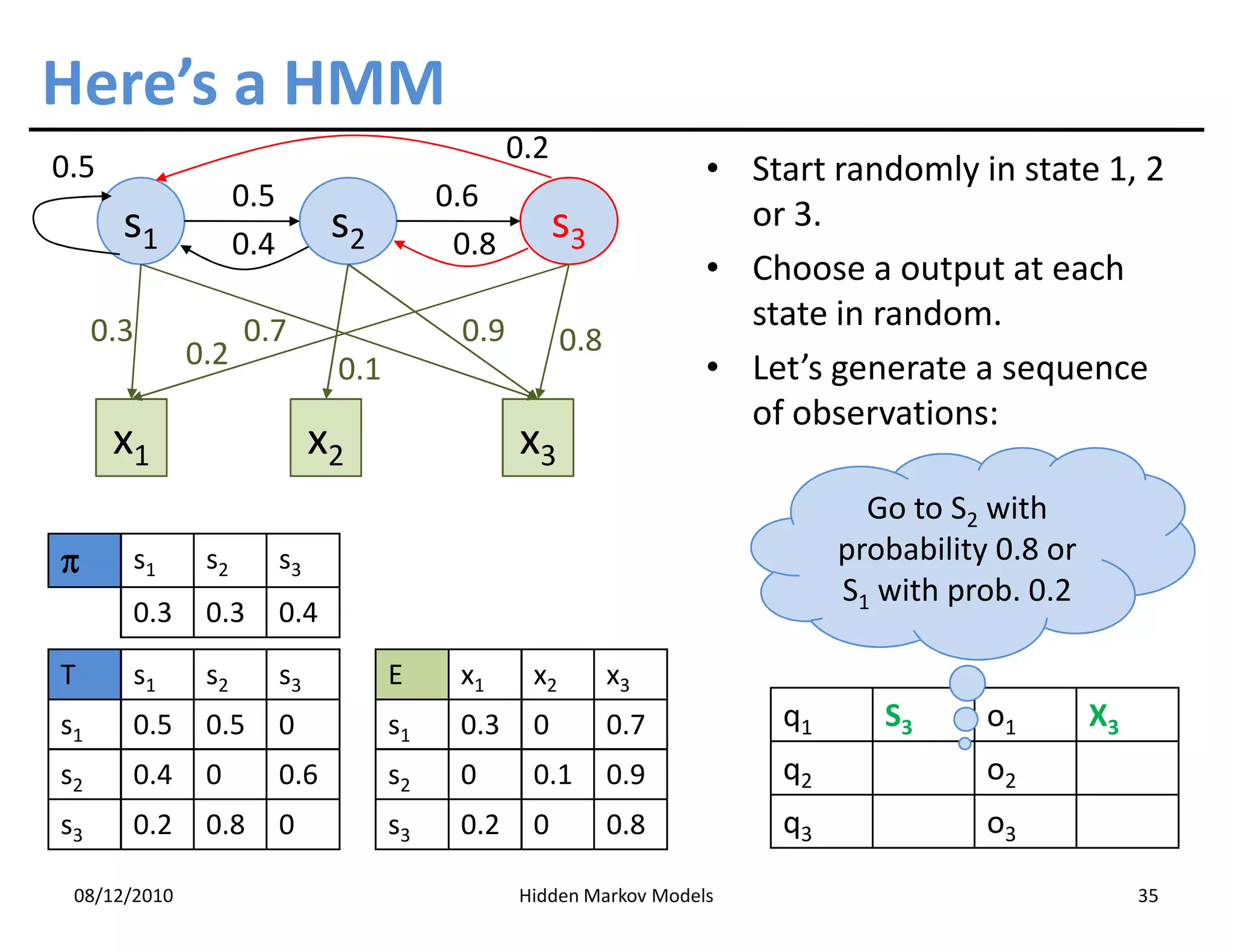
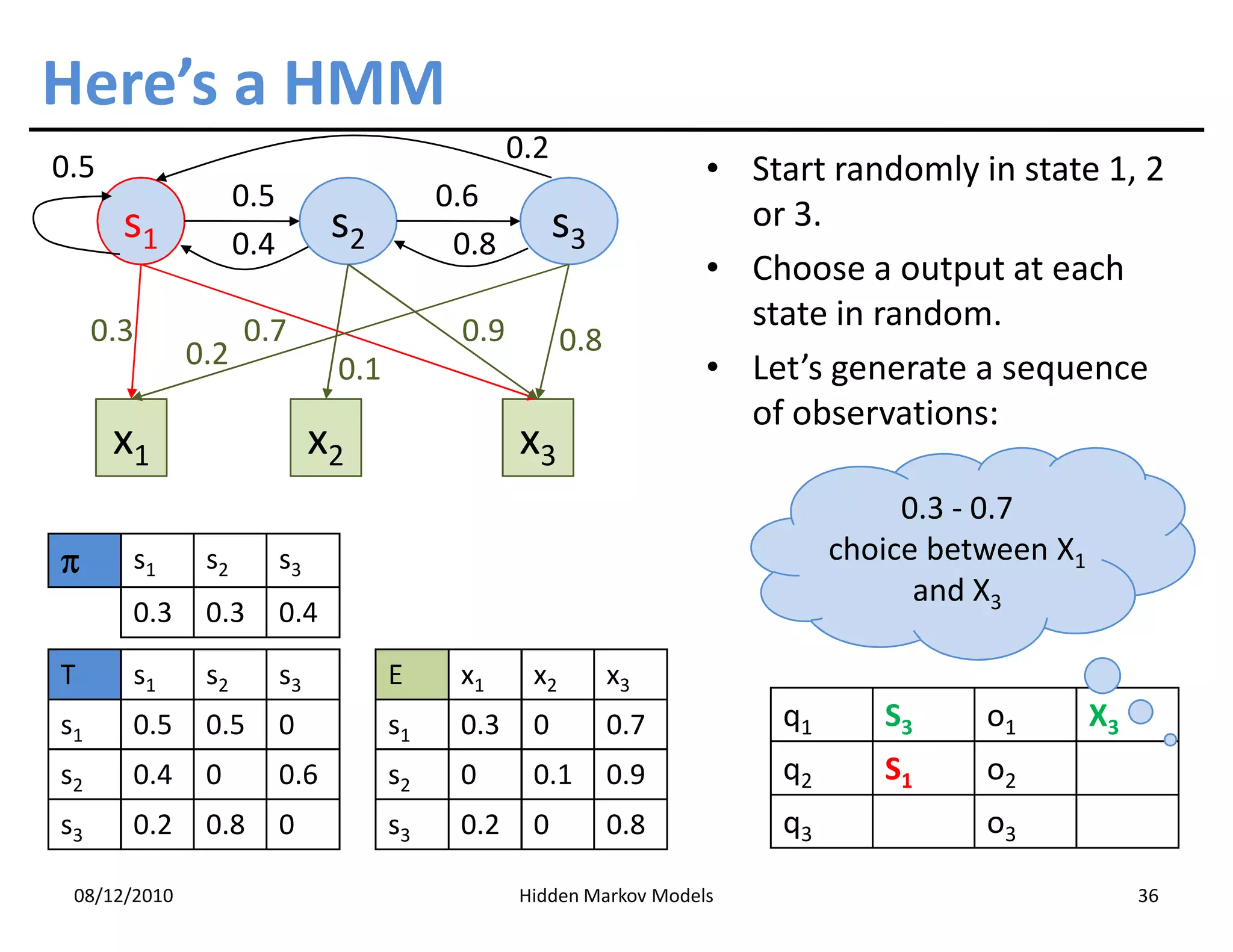
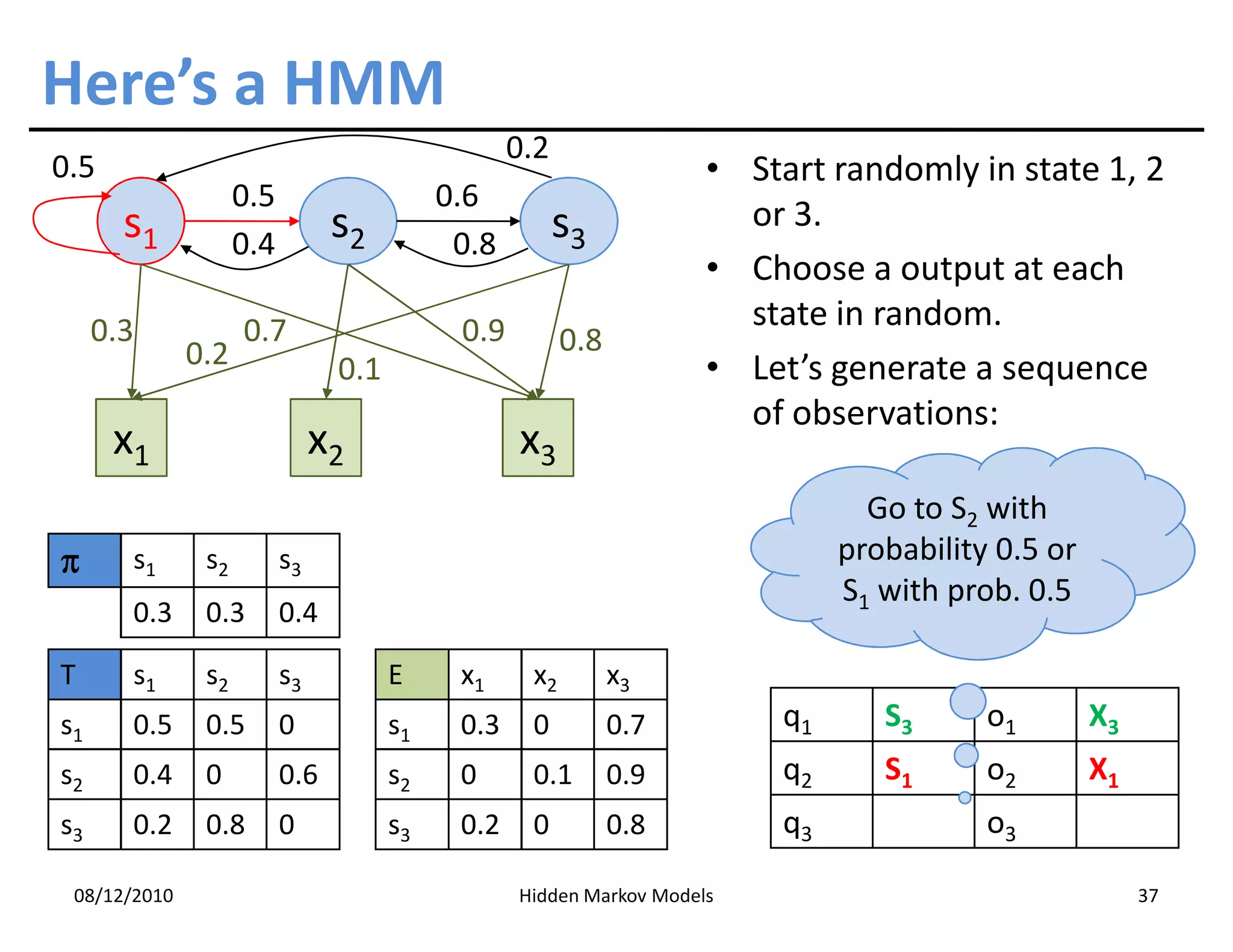
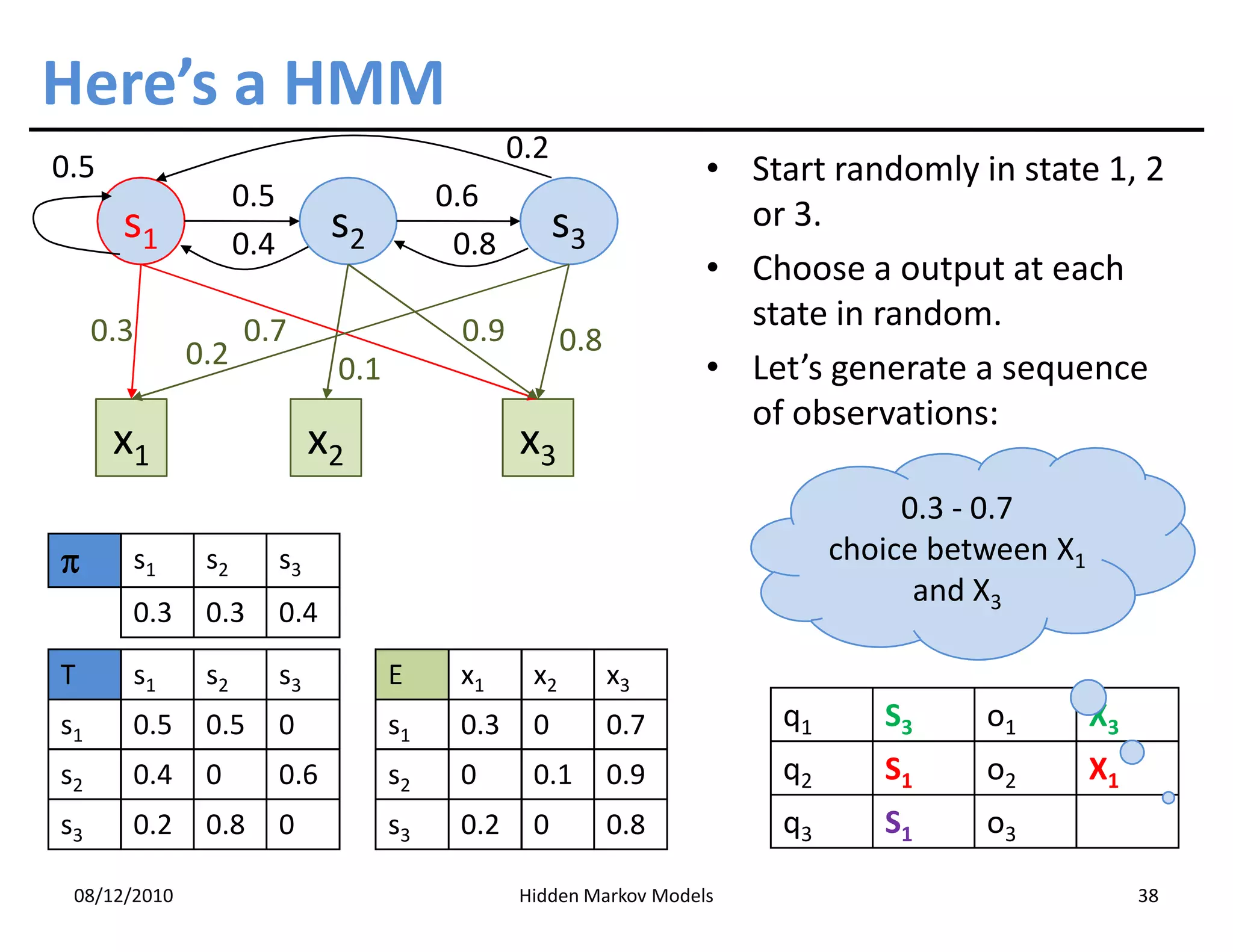
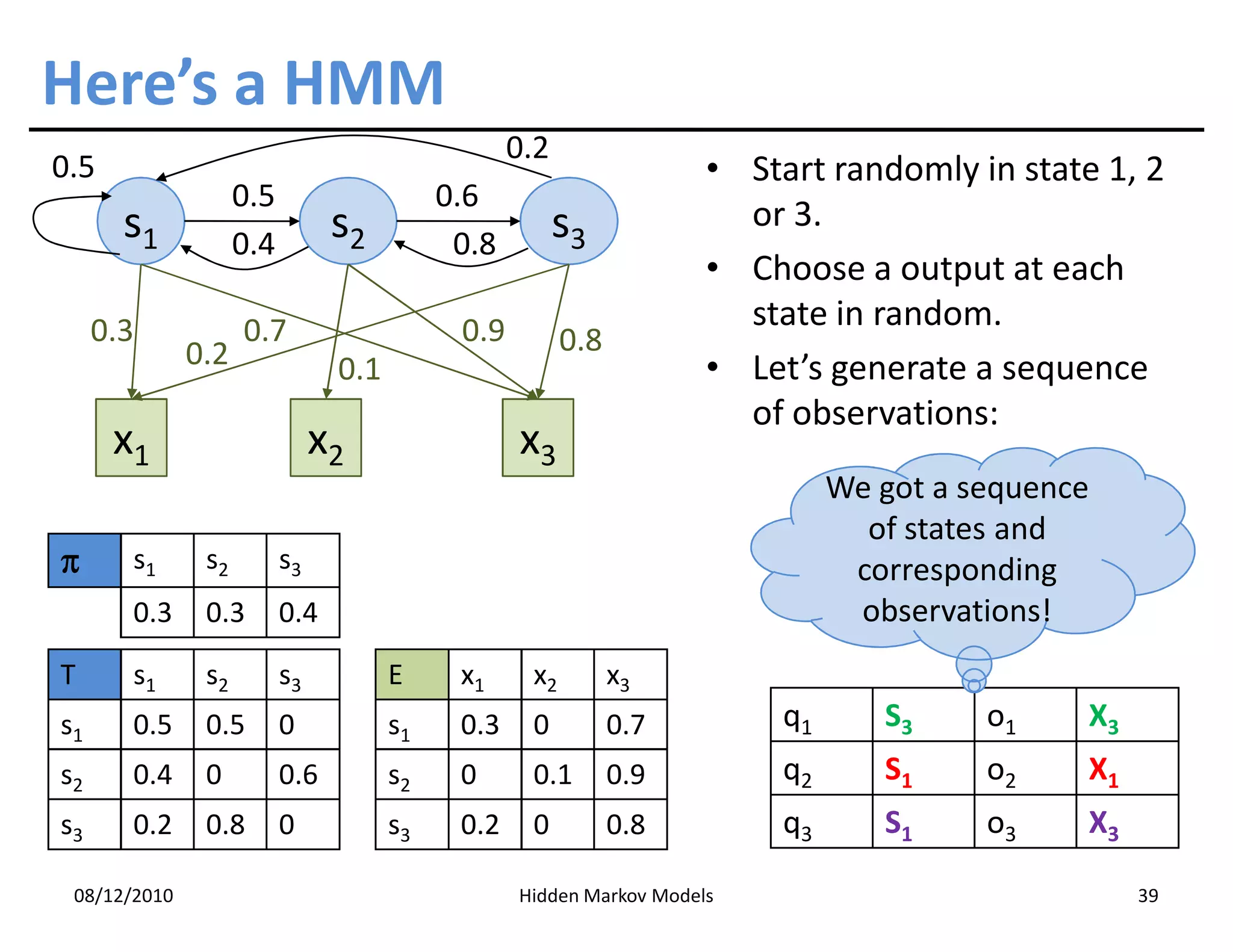
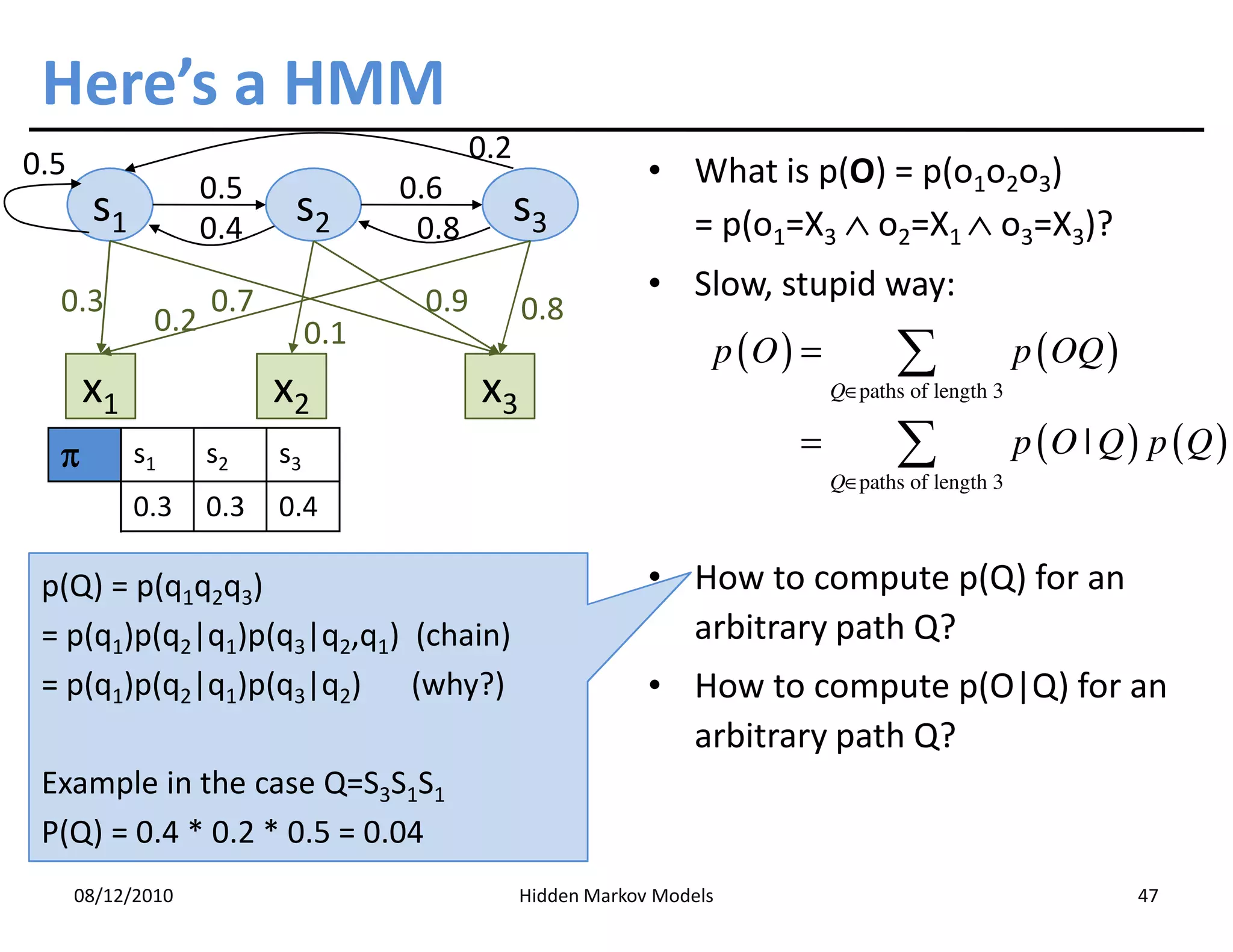
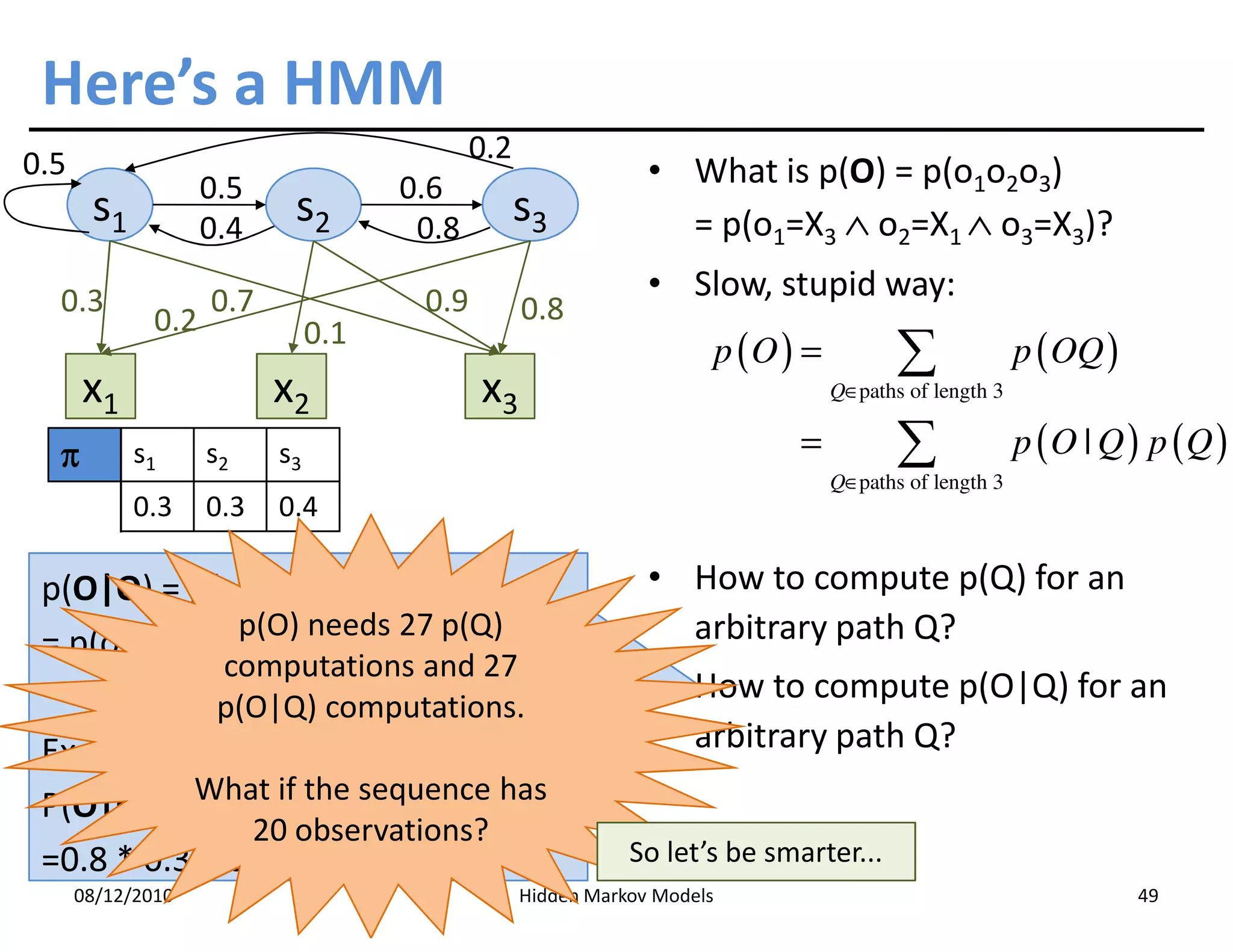
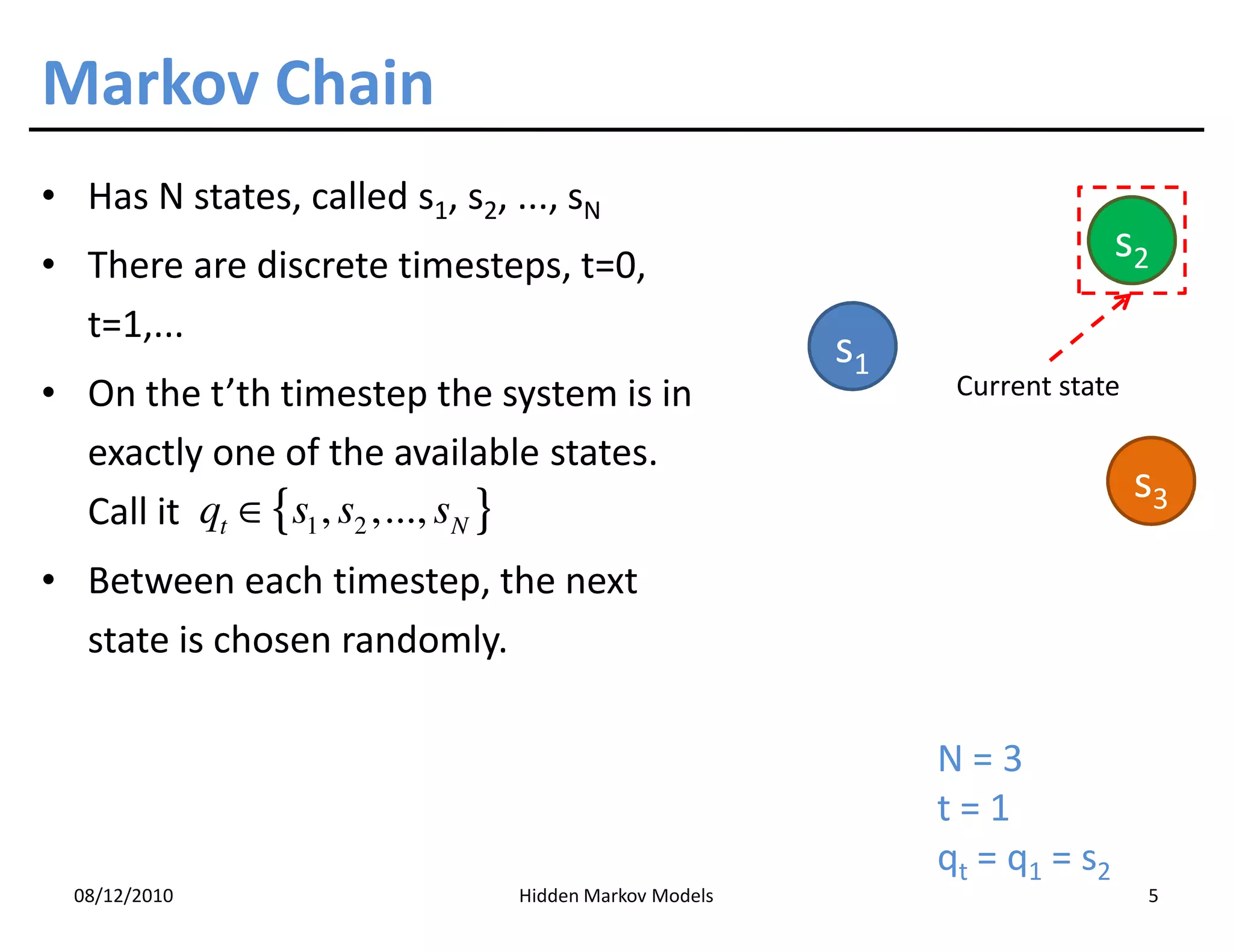
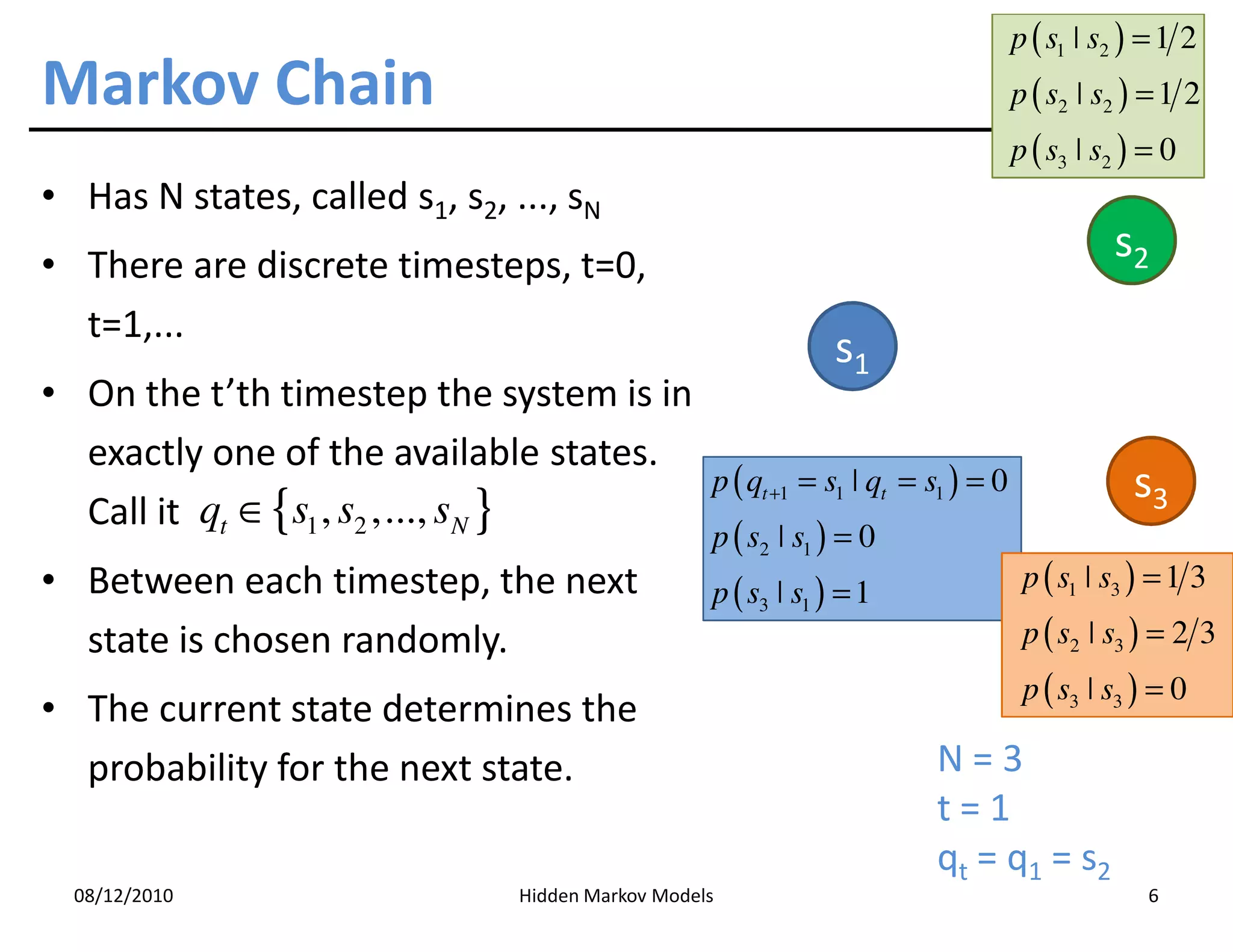
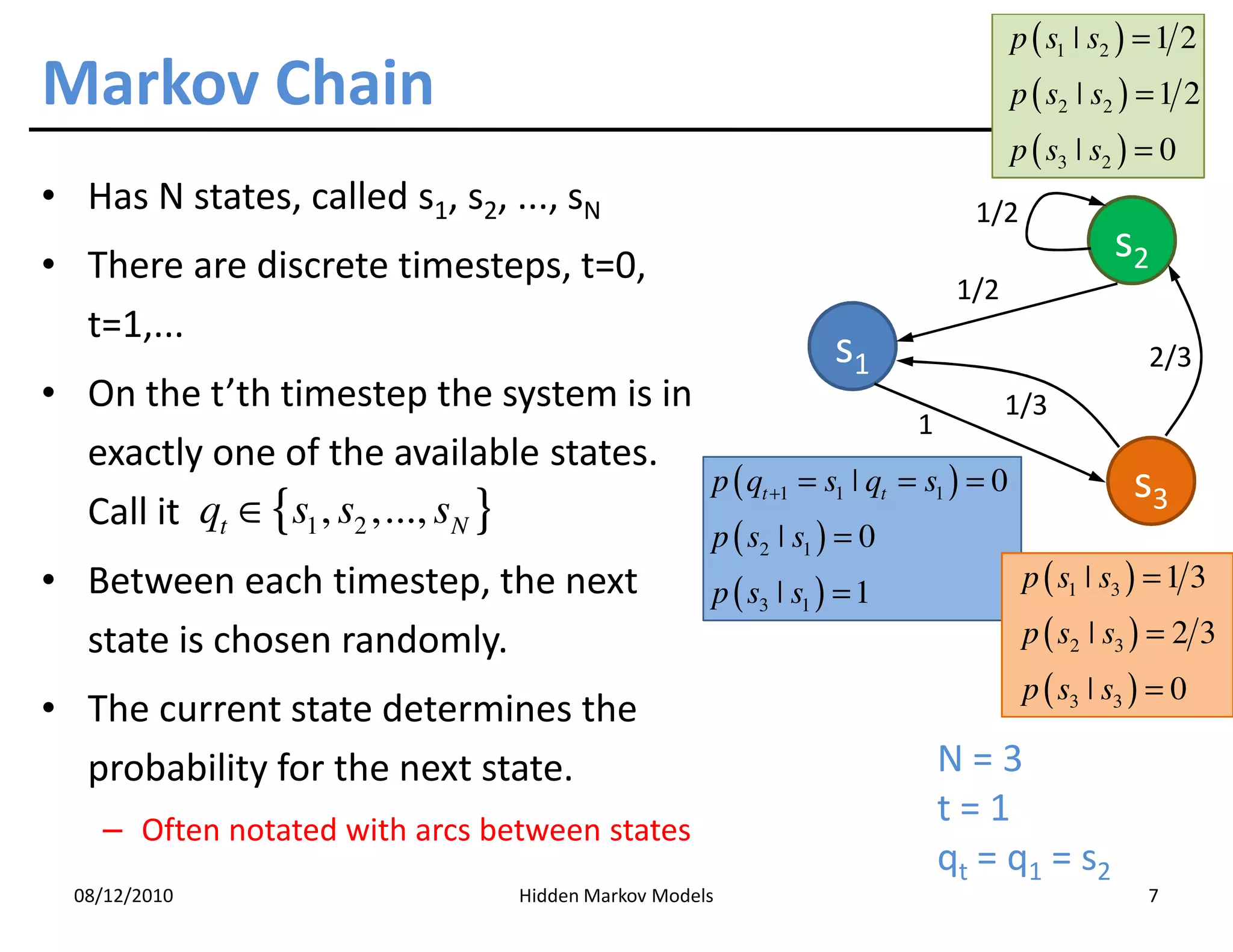
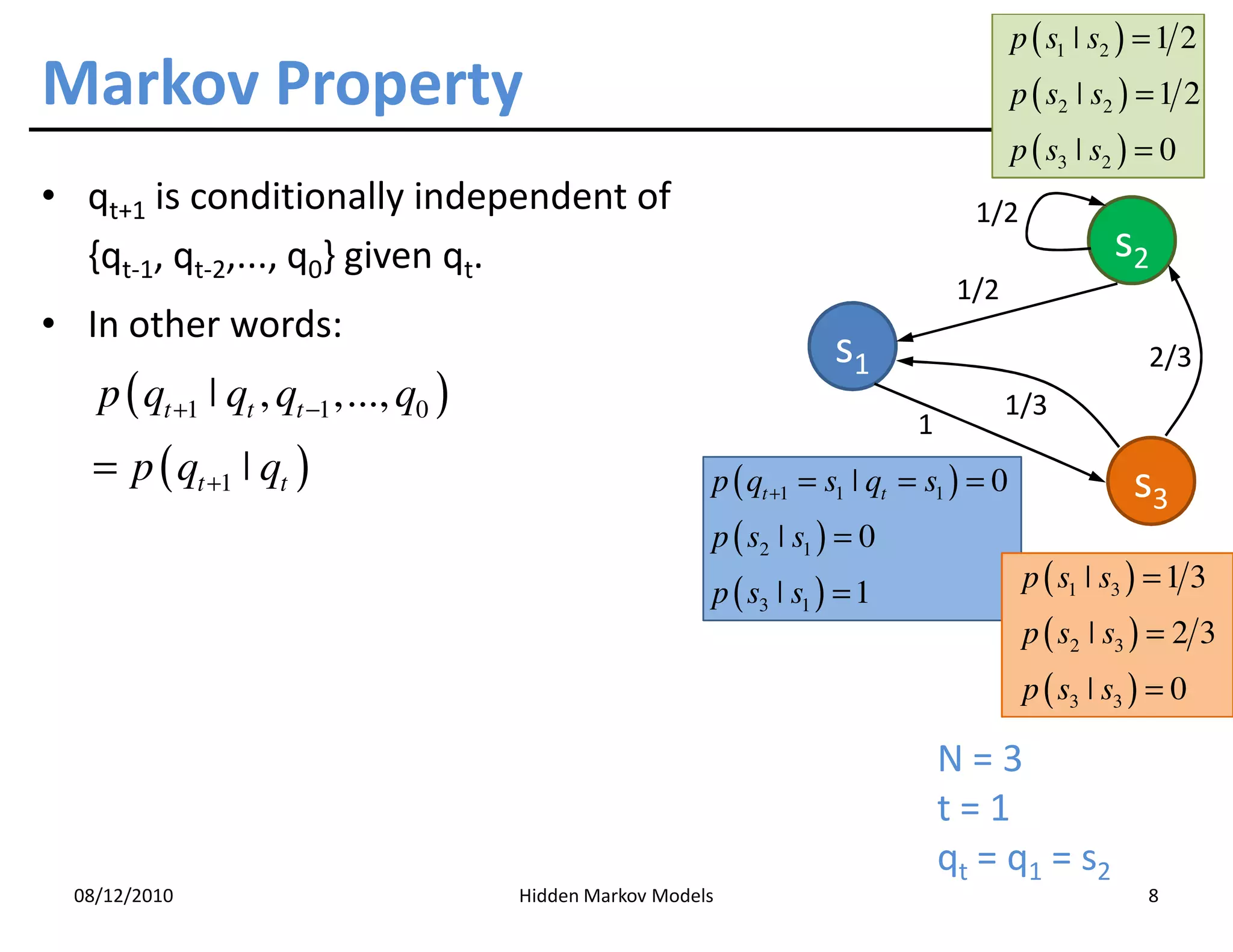
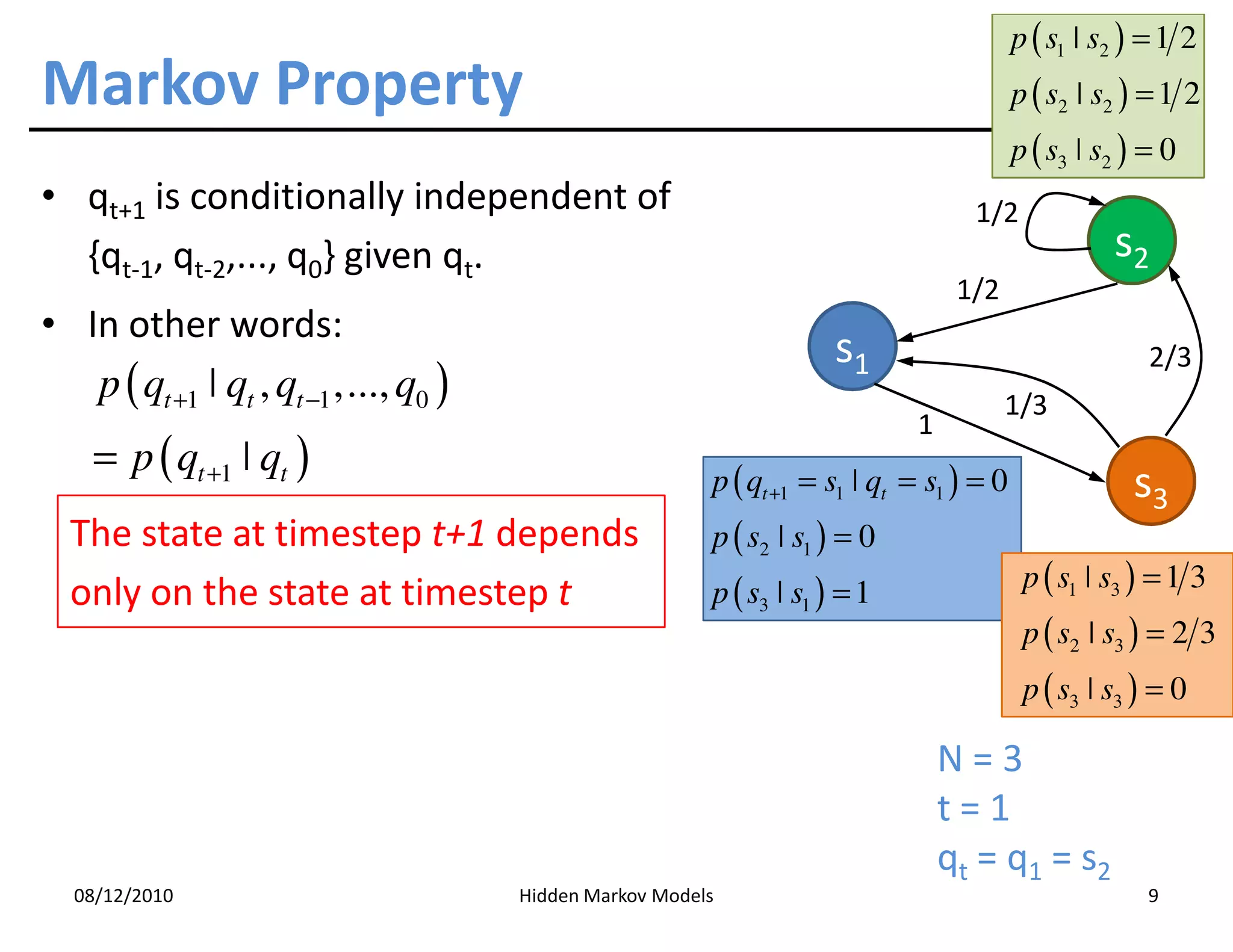
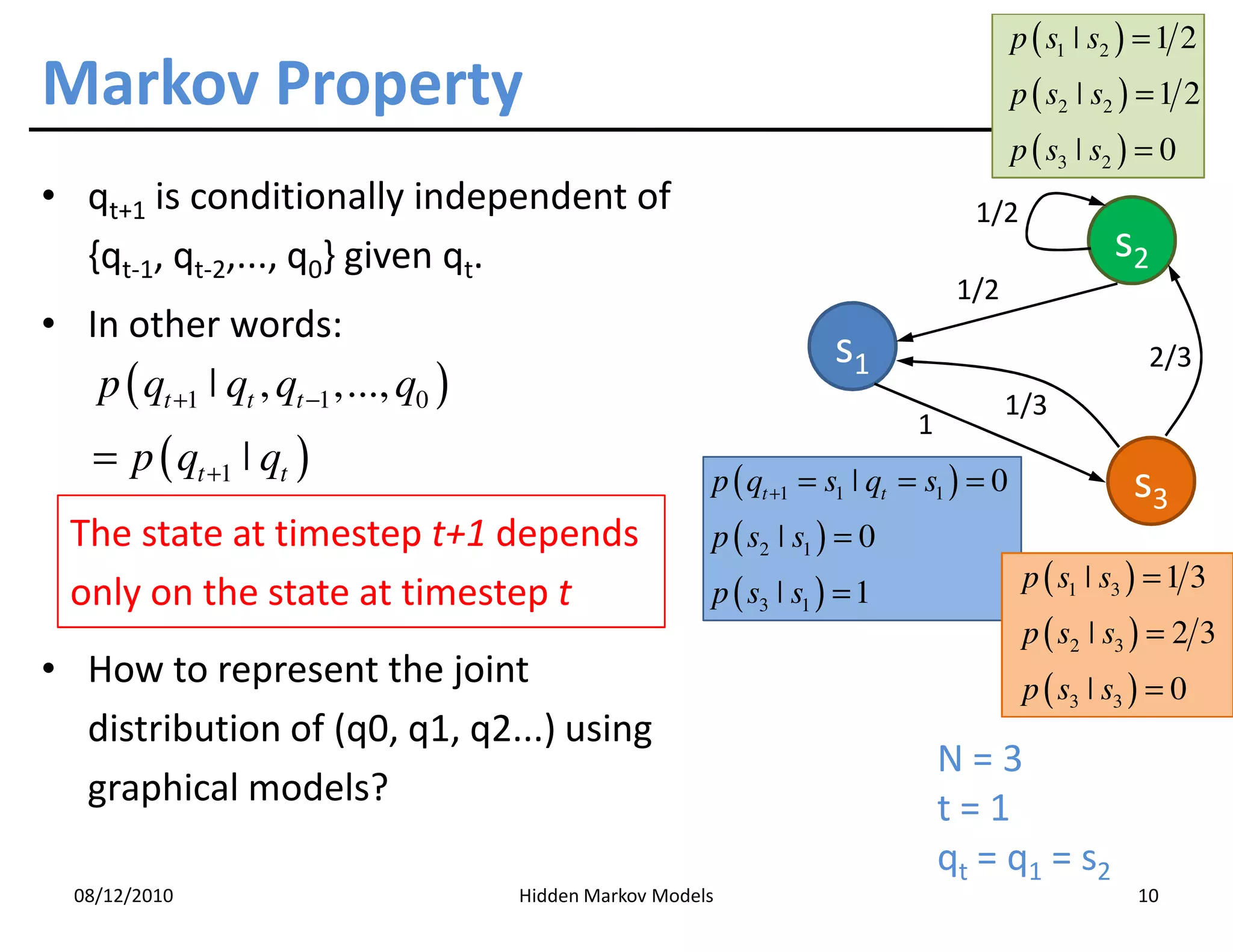
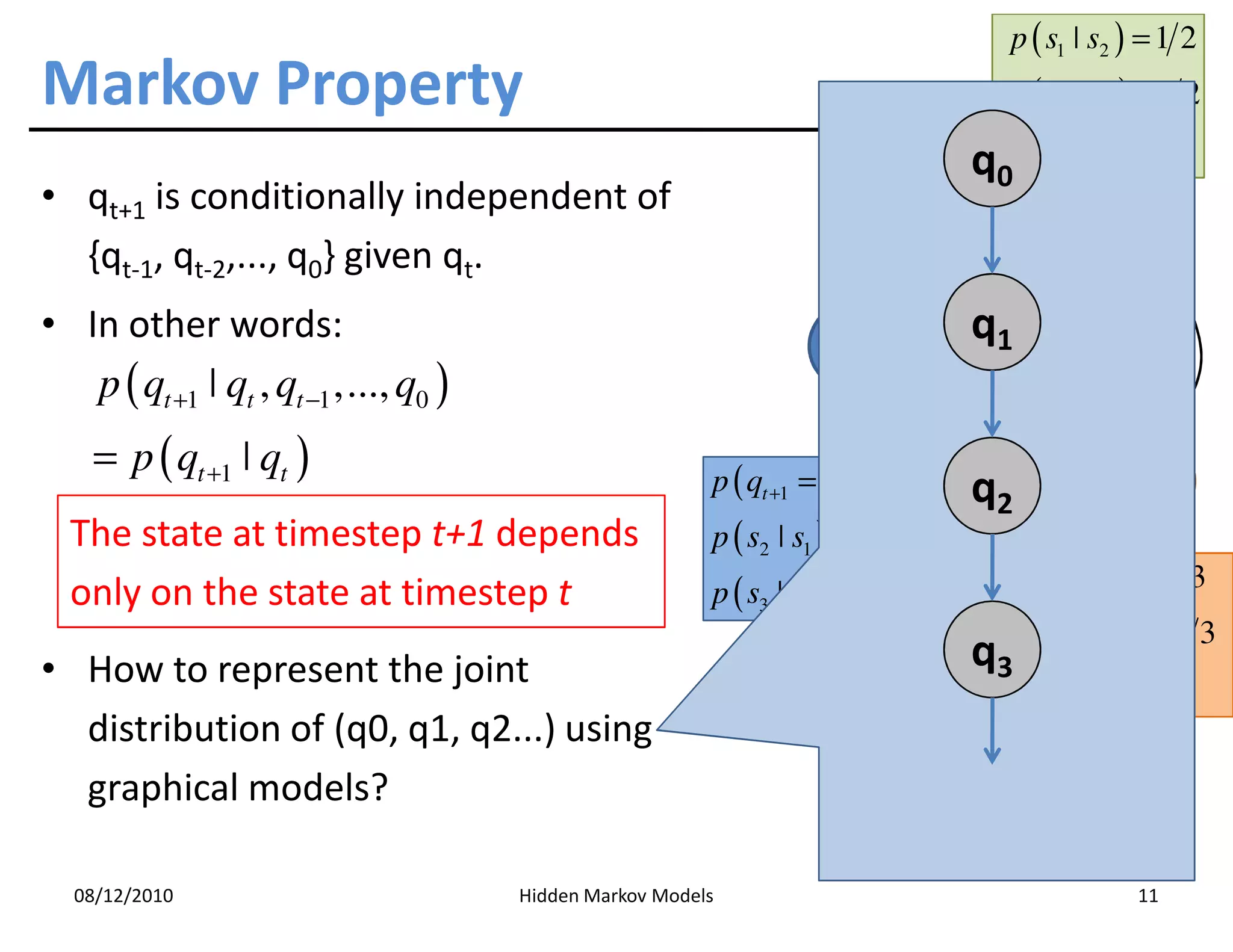
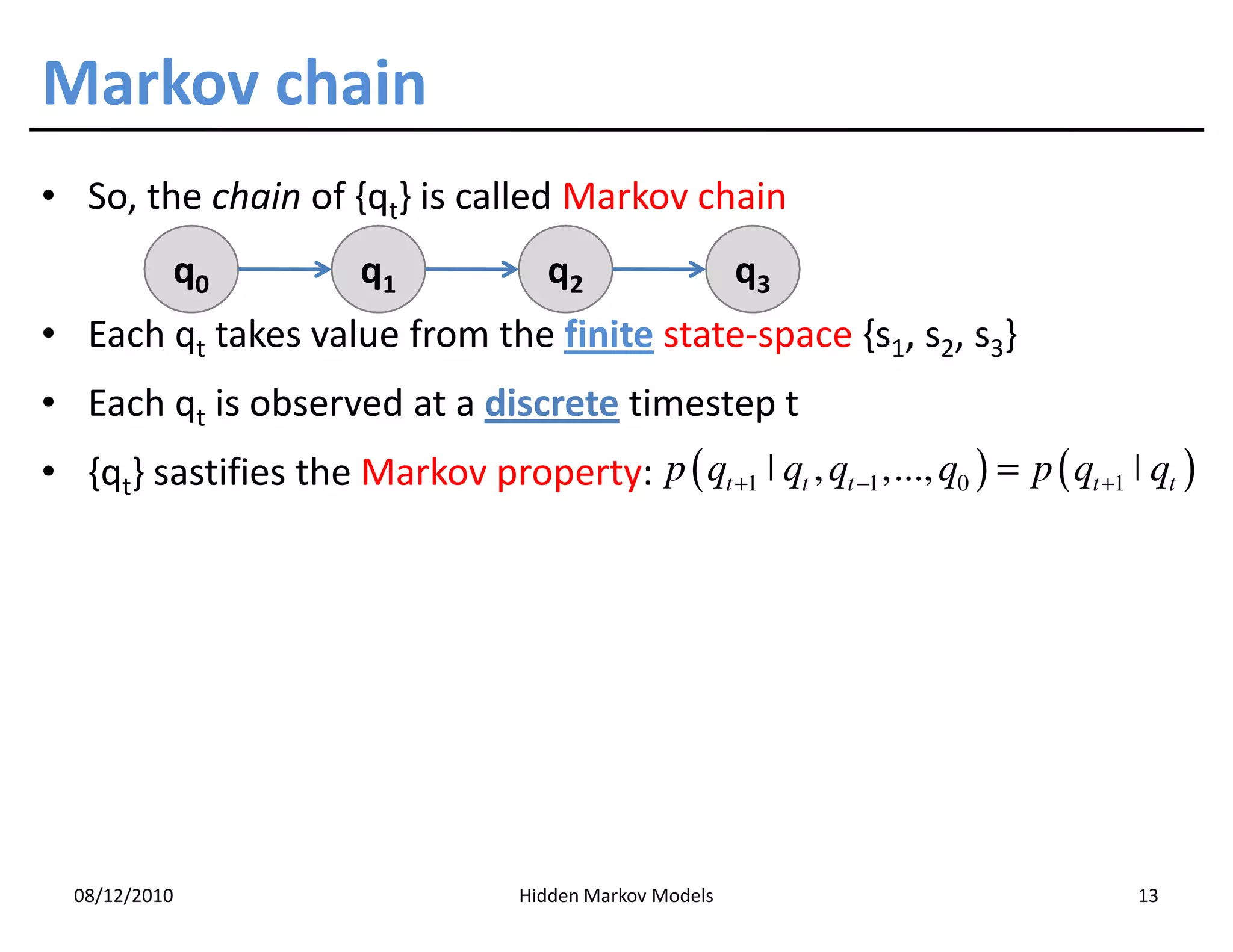
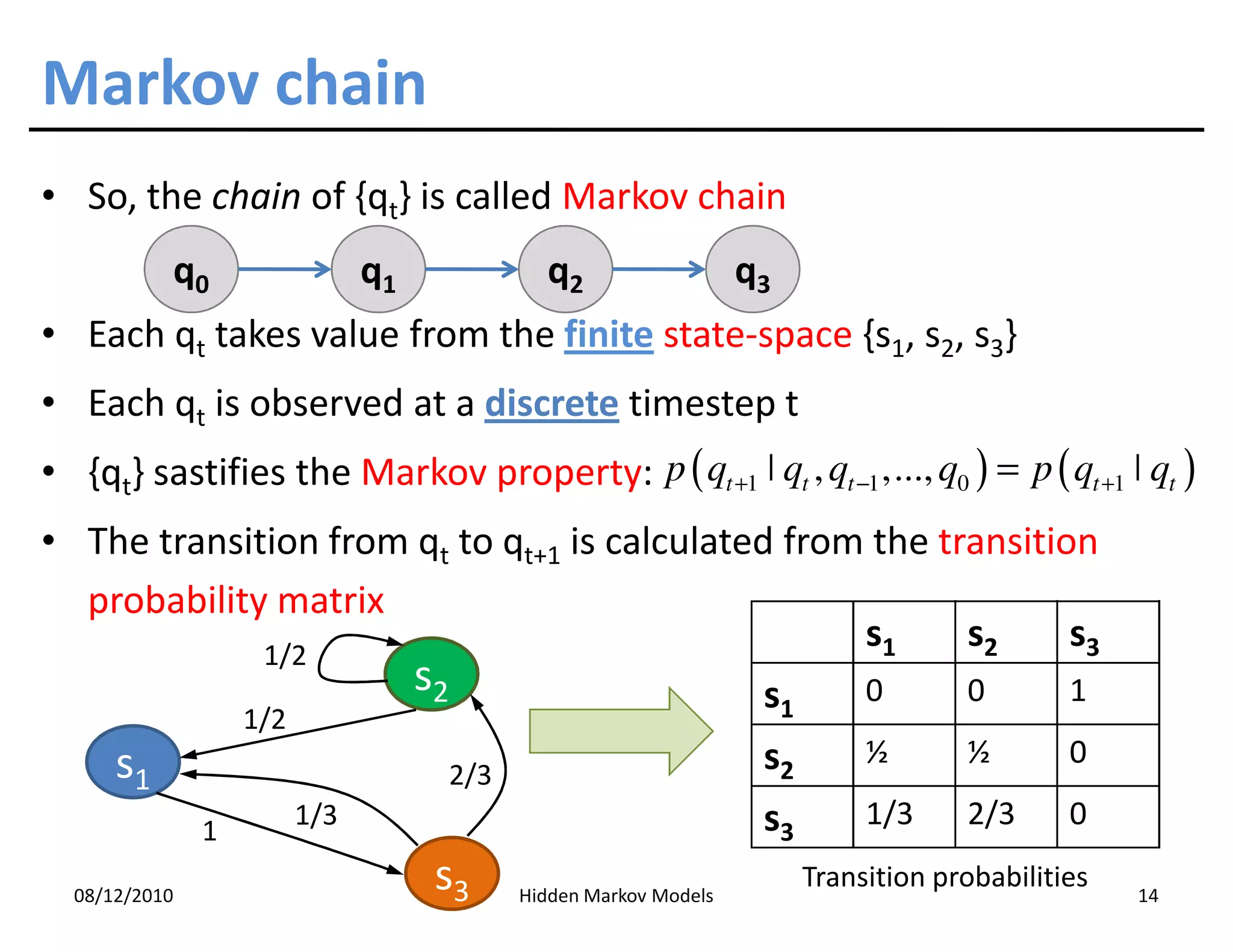
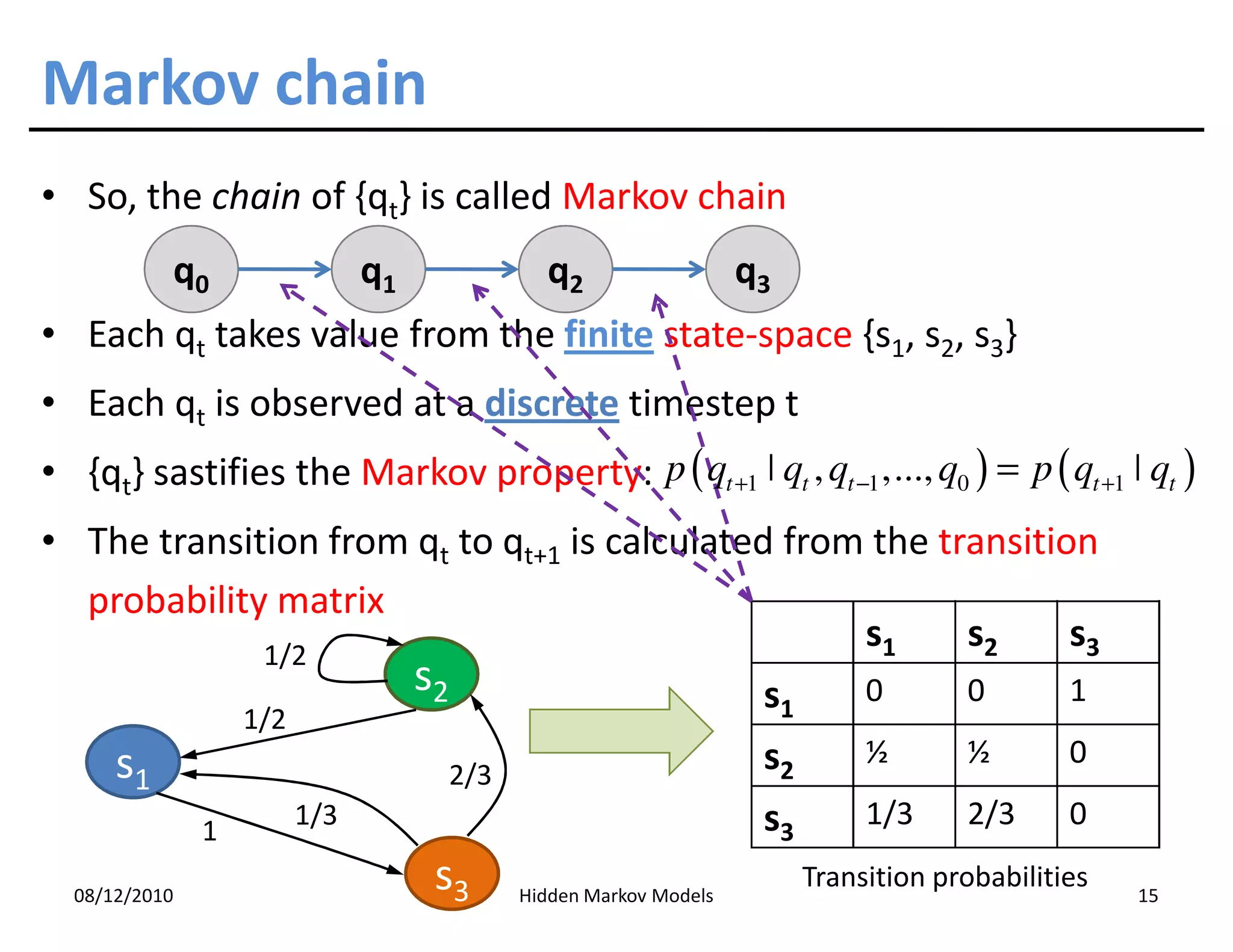
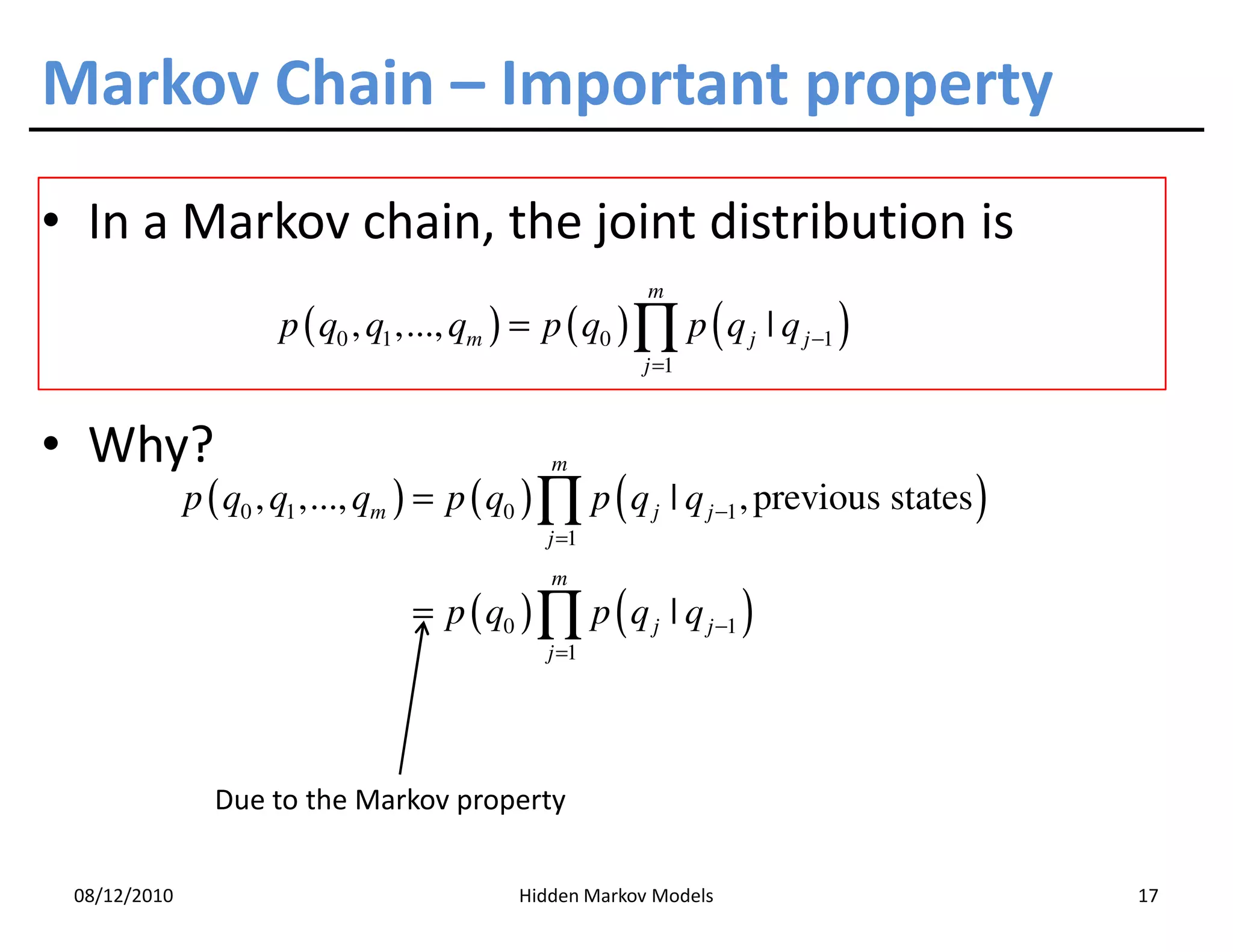
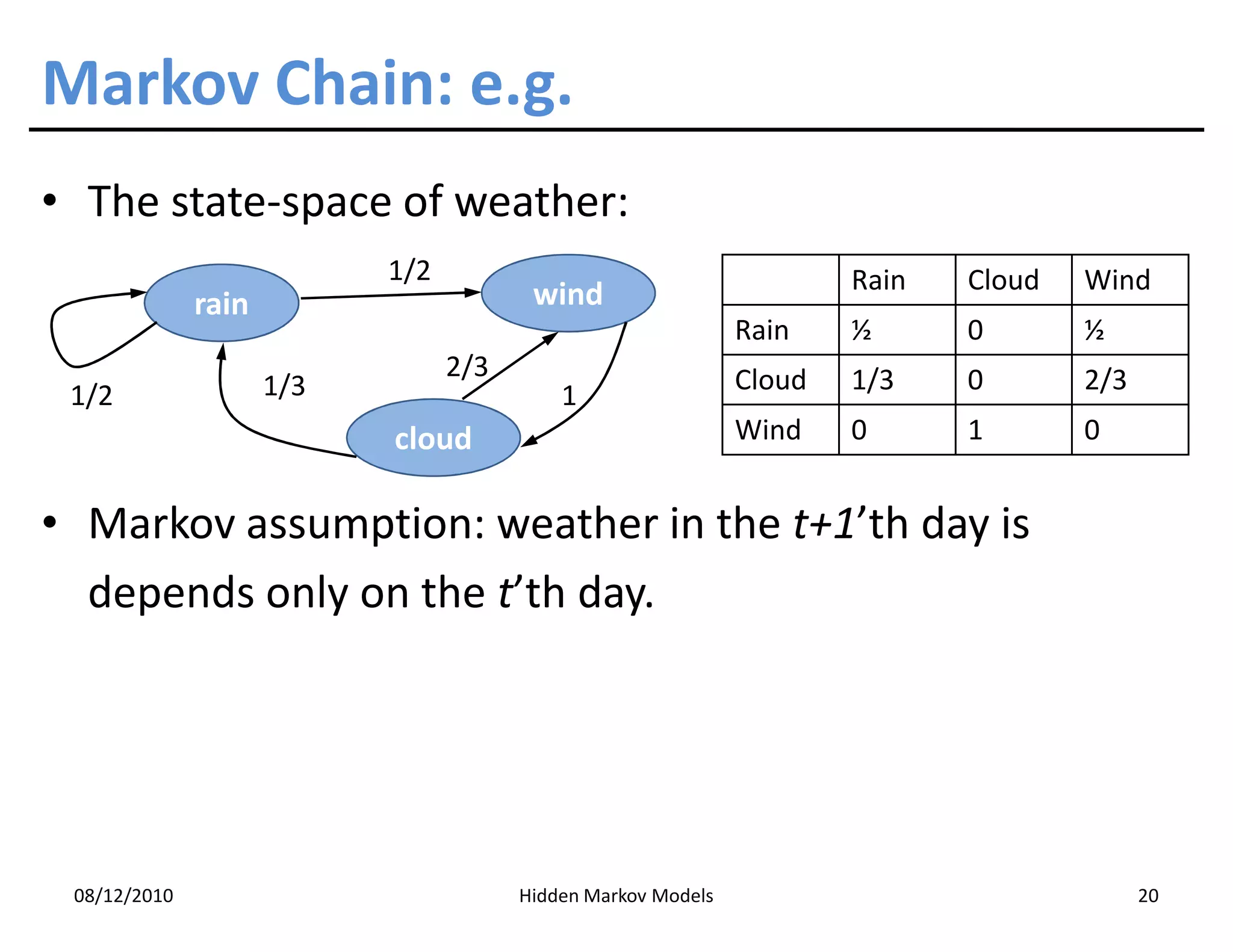
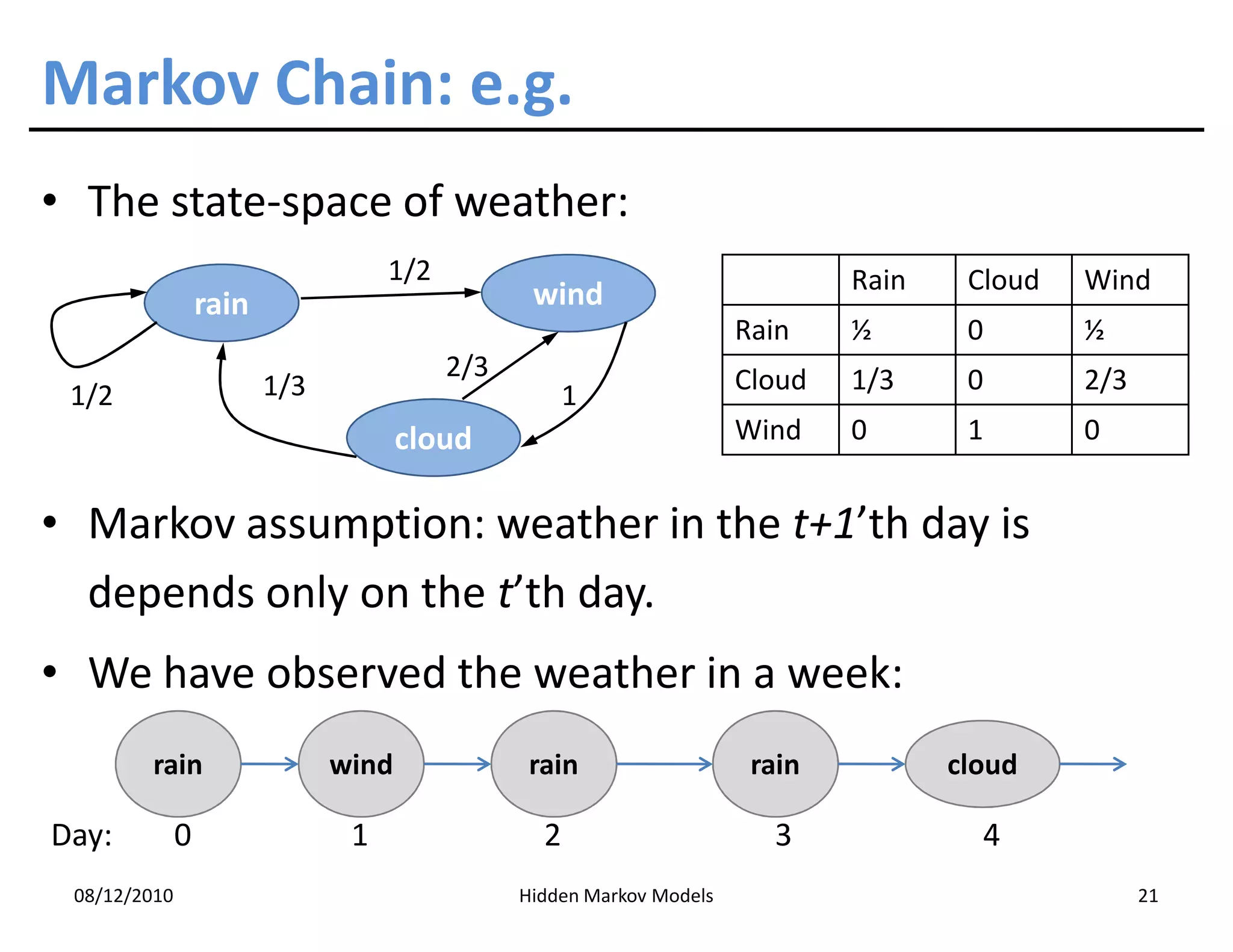
This document discusses Hidden Markov Models (HMMs) and Markov chains. It begins with an introduction to Markov processes and how HMMs are used in various domains like natural language processing. It then describes the properties of a Markov chain, which has a set of states that the system transitions between randomly at discrete time steps based on transition probabilities. The Markov property is explained as the conditional independence of future states from past states given the present state. HMMs extend Markov chains by making the state sequence hidden and only allowing observation of the output states.

1. MACHINE LEARNING
Hidden Markov Models
VU H. Pham
phvu@fit.hcmus.edu.vn
Department of Computer Science
Dececmber 6th, 2010
08/12/2010 Hidden Markov Models 1

2. Contents
• Introduction
• Markov Chain
• Hidden Markov Models
08/12/2010 Hidden Markov Models 2

3. Introduction
• Markov processes are first proposed by
Russian mathematician Andrei Markov
– He used these processes to investigate
Pushkin’s poem.
• Nowaday, Markov property and HMMs are
widely used in many domains:
– Natural Language Processing
– Speech Recognition
– Bioinformatics
– Image/video processing
– ...
08/12/2010 Hidden Markov Models 3

4. Markov Chain
• Has N states, called s1, s2, ..., sN
• There are discrete timesteps, t=0,
s2
t=1,...
s1
• On the t’th timestep the system is in
exactly one of the available states.
s3
Call it qt ∈ {s1 , s2 ,..., sN }
Current state
N=3
t=0
q t = q 0 = s3
08/12/2010 Hidden Markov Models 4

5. Markov Chain
• Has N states, called s1, s2, ..., sN
• There are discrete timesteps, t=0,
s2
t=1,...
s1
• On the t’th timestep the system is in Current state
exactly one of the available states.
s3
Call it qt ∈ {s1 , s2 ,..., sN }
• Between each timestep, the next
state is chosen randomly.
N=3
t=1
q t = q 1 = s2
08/12/2010 Hidden Markov Models 5

6. p ( s1 ˚ s2 ) = 1 2
Markov Chain p ( s2 ˚ s2 ) = 1 2
p ( s3 ˚ s2 ) = 0
• Has N states, called s1, s2, ..., sN
• There are discrete timesteps, t=0,
s2
t=1,...
s1
• On the t’th timestep the system is in
exactly one of the available states.
p ( qt +1 = s1 ˚ qt = s1 ) = 0 s3
Call it qt ∈ {s1 , s2 ,..., sN }
p ( s2 ˚ s1 ) = 0
• Between each timestep, the next p ( s3 ˚ s1 ) = 1 p ( s1 ˚ s3 ) = 1 3
state is chosen randomly. p ( s2 ˚ s3 ) = 2 3
p ( s3 ˚ s3 ) = 0
• The current state determines the
probability for the next state. N=3
t=1
q t = q 1 = s2
08/12/2010 Hidden Markov Models 6

7. p ( s1 ˚ s2 ) = 1 2
Markov Chain p ( s2 ˚ s2 ) = 1 2
p ( s3 ˚ s2 ) = 0
• Has N states, called s1, s2, ..., sN 1/2
• There are discrete timesteps, t=0,
s2
1/2
t=1,...
s1 2/3
• On the t’th timestep the system is in 1/3
1
exactly one of the available states.
p ( qt +1 = s1 ˚ qt = s1 ) = 0 s3
Call it qt ∈ {s1 , s2 ,..., sN }
p ( s2 ˚ s1 ) = 0
• Between each timestep, the next p ( s3 ˚ s1 ) = 1 p ( s1 ˚ s3 ) = 1 3
state is chosen randomly. p ( s2 ˚ s3 ) = 2 3
p ( s3 ˚ s3 ) = 0
• The current state determines the
probability for the next state. N=3
– Often notated with arcs between states
t=1
q t = q 1 = s2
08/12/2010 Hidden Markov Models 7

8. p ( s1 ˚ s2 ) = 1 2
Markov Property p ( s2 ˚ s2 ) = 1 2
p ( s3 ˚ s2 ) = 0
• qt+1 is conditionally independent of 1/2
{qt-1, qt-2,..., q0} given qt. s2
1/2
• In other words:
s1 2/3
p ( qt +1 ˚ qt , qt −1 ,..., q0 ) 1/3
1
= p ( qt +1 ˚ qt ) p ( qt +1 = s1 ˚ qt = s1 ) = 0 s3
p ( s2 ˚ s1 ) = 0
p ( s3 ˚ s1 ) = 1 p ( s1 ˚ s3 ) = 1 3
p ( s2 ˚ s3 ) = 2 3
p ( s3 ˚ s3 ) = 0
N=3
t=1
q t = q 1 = s2
08/12/2010 Hidden Markov Models 8

9. p ( s1 ˚ s2 ) = 1 2
Markov Property p ( s2 ˚ s2 ) = 1 2
p ( s3 ˚ s2 ) = 0
• qt+1 is conditionally independent of 1/2
{qt-1, qt-2,..., q0} given qt. s2
1/2
• In other words:
s1 2/3
p ( qt +1 ˚ qt , qt −1 ,..., q0 ) 1/3
1
= p ( qt +1 ˚ qt ) p ( qt +1 = s1 ˚ qt = s1 ) = 0 s3
The state at timestep t+1 depends p ( s2 ˚ s1 ) = 0
p ( s3 ˚ s1 ) = 1 p ( s1 ˚ s3 ) = 1 3
only on the state at timestep t
p ( s2 ˚ s3 ) = 2 3
p ( s3 ˚ s3 ) = 0
N=3
t=1
q t = q 1 = s2
08/12/2010 Hidden Markov Models 9

10. p ( s1 ˚ s2 ) = 1 2
Markov Property p ( s2 ˚ s2 ) = 1 2
p ( s3 ˚ s2 ) = 0
• qt+1 is conditionally independent of 1/2
{qt-1, qt-2,..., q0} given qt. s2
1/2
• In other words:
s1 2/3
p ( qt +1 ˚ qt , qt −1 ,..., q0 ) 1/3
1
= p ( qt +1 ˚ qt ) p ( qt +1 = s1 ˚ qt = s1 ) = 0 s3
The state at timestep t+1 depends p ( s2 ˚ s1 ) = 0
p ( s3 ˚ s1 ) = 1 p ( s1 ˚ s3 ) = 1 3
only on the state at timestep t
p ( s2 ˚ s3 ) = 2 3
• How to represent the joint p ( s3 ˚ s3 ) = 0
distribution of (q0, q1, q2...) using
N=3
graphical models? t=1
q t = q 1 = s2
08/12/2010 Hidden Markov Models 10

11. p ( s1 ˚ s2 ) = 1 2
Markov Property p ( s2 ˚ s2 ) = 1 2
q0p ( s 3 ˚ s2 ) = 0
• qt+1 is conditionally independent of 1/2
{qt-1, qt-2,..., q0} given qt. s2
1/2
• In other words: q1
s1 1/3
p ( qt +1 ˚ qt , qt −1 ,..., q0 ) 1/3
1
= p ( qt +1 ˚ qt ) p ( qt +1 = s1 ˚ qt = s1 ) = 0
q2 s3
The state at timestep t+1 depends p ( s2 ˚ s1 ) = 0
p ( s3 ˚ s1 ) = 1 p ( s1 ˚ s3 ) = 1 3
only on the state at timestep t
• How to represent the joint q3 p ( s 2 ˚ s3 ) = 2 3
p ( s3 ˚ s3 ) = 0
distribution of (q0, q1, q2...) using
N=3
graphical models? t=1
q t = q 1 = s2
08/12/2010 Hidden Markov Models 11

12. Markov chain
• So, the chain of {qt} is called Markov chain
q0 q1 q2 q3
08/12/2010 Hidden Markov Models 12

13. Markov chain
• So, the chain of {qt} is called Markov chain
q0 q1 q2 q3
• Each qt takes value from the finite state-space {s1, s2, s3}
• Each qt is observed at a discrete timestep t
• {qt} sastifies the Markov property: p ( qt +1 ˚ qt , qt −1 ,..., q0 ) = p ( qt +1 ˚ qt )
08/12/2010 Hidden Markov Models 13

14. Markov chain
• So, the chain of {qt} is called Markov chain
q0 q1 q2 q3
• Each qt takes value from the finite state-space {s1, s2, s3}
• Each qt is observed at a discrete timestep t
• {qt} sastifies the Markov property: p ( qt +1 ˚ qt , qt −1 ,..., q0 ) = p ( qt +1 ˚ qt )
• The transition from qt to qt+1 is calculated from the transition
probability matrix
1/2
s1 s2 s3
s2 s1 0 0 1
1/2
s1 s2 ½ ½ 0
2/3
1
1/3 s3 1/3 2/3 0
08/12/2010
s3 Hidden Markov Models
Transition probabilities
14

15. Markov chain
• So, the chain of {qt} is called Markov chain
q0 q1 q2 q3
• Each qt takes value from the finite state-space {s1, s2, s3}
• Each qt is observed at a discrete timestep t
• {qt} sastifies the Markov property: p ( qt +1 ˚ qt , qt −1 ,..., q0 ) = p ( qt +1 ˚ qt )
• The transition from qt to qt+1 is calculated from the transition
probability matrix
1/2
s1 s2 s3
s2 s1 0 0 1
1/2
s1 s2 ½ ½ 0
2/3
1
1/3 s3 1/3 2/3 0
08/12/2010
s3 Hidden Markov Models
Transition probabilities
15

16. Markov Chain – Important property
• In a Markov chain, the joint distribution is
m
p ( q0 , q1 ,..., qm ) = p ( q0 ) ∏ p ( q j | q j −1 )
j =1
08/12/2010 Hidden Markov Models 16

17. Markov Chain – Important property
• In a Markov chain, the joint distribution is
m
p ( q0 , q1 ,..., qm ) = p ( q0 ) ∏ p ( q j | q j −1 )
j =1
• Why? m
p ( q0 , q1 ,..., qm ) = p ( q0 ) ∏ p ( q j | q j −1 , previous states )
j =1
m
= p ( q0 ) ∏ p ( q j | q j −1 )
j =1
Due to the Markov property
08/12/2010 Hidden Markov Models 17

18. Markov Chain: e.g.
• The state-space of weather:
rain wind
cloud
08/12/2010 Hidden Markov Models 18

19. Markov Chain: e.g.
• The state-space of weather:
1/2 Rain Cloud Wind
rain wind
Rain ½ 0 ½
2/3 Cloud 1/3 0 2/3
1/2 1/3 1
cloud Wind 0 1 0
08/12/2010 Hidden Markov Models 19

20. Markov Chain: e.g.
• The state-space of weather:
1/2 Rain Cloud Wind
rain wind
Rain ½ 0 ½
2/3 Cloud 1/3 0 2/3
1/2 1/3 1
cloud Wind 0 1 0
• Markov assumption: weather in the t+1’th day is
depends only on the t’th day.
08/12/2010 Hidden Markov Models 20

21. Markov Chain: e.g.
• The state-space of weather:
1/2 Rain Cloud Wind
rain wind
Rain ½ 0 ½
2/3 Cloud 1/3 0 2/3
1/2 1/3 1
cloud Wind 0 1 0
• Markov assumption: weather in the t+1’th day is
depends only on the t’th day.
• We have observed the weather in a week:
rain wind rain rain cloud
Day: 0 1 2 3 4
08/12/2010 Hidden Markov Models 21

22. Markov Chain: e.g.
• The state-space of weather:
1/2 Rain Cloud Wind
rain wind
Rain ½ 0 ½
2/3 Cloud 1/3 0 2/3
1/2 1/3 1
cloud Wind 0 1 0
• Markov assumption: weather in the t+1’th day is
depends only on the t’th day.
• We have observed the weather in a week: Markov Chain
rain wind rain rain cloud
Day: 0 1 2 3 4
08/12/2010 Hidden Markov Models 22

23. Contents
• Introduction
• Markov Chain
• Hidden Markov Models
08/12/2010 Hidden Markov Models 23

24. Modeling pairs of sequences
• In many applications, we have to model pair of sequences
• Examples:
– POS tagging in Natural Language Processing (assign each word in a
sentence to Noun, Adj, Verb...)
– Speech recognition (map acoustic sequences to sequences of words)
– Computational biology (recover gene boundaries in DNA sequences)
– Video tracking (estimate the underlying model states from the observation
sequences)
– And many others...
08/12/2010 Hidden Markov Models 24

25. Probabilistic models for sequence pairs
• We have two sequences of random variables:
X1, X2, ..., Xm and S1, S2, ..., Sm
• Intuitively, in a pratical system, each Xi corresponds to an observation
and each Si corresponds to a state that generated the observation.
• Let each Si be in {1, 2, ..., k} and each Xi be in {1, 2, ..., o}
• How do we model the joint distribution:
p ( X 1 = x1 ,..., X m = xm , S1 = s1 ,..., S m = sm )
08/12/2010 Hidden Markov Models 25

26. Hidden Markov Models (HMMs)
• In HMMs, we assume that
p ( X 1 = x1 ,..., X m = xm , S1 = s1 ,..., Sm = sm )
m m
= p ( S1 = s1 ) ∏ p ( S j = s j ˚ S j −1 = s j −1 ) ∏ p ( X j = x j ˚ S j = s j )
j =2 j =1
• This is often called Independence assumptions in
HMMs
• We are gonna prove it in the next slides
08/12/2010 Hidden Markov Models 26

27. Independence Assumptions in HMMs [1]
p ( ABC ) = p ( A | BC ) p ( BC ) = p ( A | BC ) p ( B ˚ C ) p ( C )
• By the chain rule, the following equality is exact:
p ( X 1 = x1 ,..., X m = xm , S1 = s1 ,..., S m = sm )
= p ( S1 = s1 ,..., S m = sm ) ×
p ( X 1 = x1 ,..., X m = xm ˚ S1 = s1 ,..., S m = sm )
• Assumption 1: the state sequence forms a Markov chain
m
p ( S1 = s1 ,..., S m = sm ) = p ( S1 = s1 ) ∏ p ( S j = s j ˚ S j −1 = s j −1 )
j =2
08/12/2010 Hidden Markov Models 27

28. Independence Assumptions in HMMs [2]
• By the chain rule, the following equality is exact:
p ( X 1 = x1 ,..., X m = xm ˚ S1 = s1 ,..., S m = sm )
m
= ∏ p ( X j = x j ˚ S1 = s1 ,..., Sm = sm , X 1 = x1 ,..., X j −1 = x j −1 )
j =1
• Assumption 2: each observation depends only on the underlying
state
p ( X j = x j ˚ S1 = s1 ,..., Sm = sm , X 1 = x1 ,..., X j −1 = x j −1 )
= p( X j = xj ˚ S j = sj )
• These two assumptions are often called independence
assumptions in HMMs
08/12/2010 Hidden Markov Models 28

29. The Model form for HMMs
• The model takes the following form:
m m
p ( x1 ,.., xm , s1 ,..., sm ;θ ) = π ( s1 ) ∏ t ( s j ˚ s j −1 ) ∏ e ( x j ˚ s j )
j =2 j =1
• Parameters in the model:
– Initial probabilities π ( s ) for s ∈ {1, 2,..., k }
– Transition probabilities t ( s ˚ s′ ) for s, s ' ∈ {1, 2,..., k }
– Emission probabilities e ( x ˚ s ) for s ∈ {1, 2,..., k }
and x ∈ {1, 2,.., o}
08/12/2010 Hidden Markov Models 29

30. 6 components of HMMs
start
• Discrete timesteps: 1, 2, ...
• Finite state space: {si} π1 π2 π3
• Events {xi} t31
t11
t12 t23
π
• Vector of initial probabilities {πi} s1 s2 s3
t21 t32
πi = p(q0 = si)
• Matrix of transition probabilities e13
e11 e23 e33
e31
T = {tij} = { p(qt+1=sj|qt=si) } e22
• Matrix of emission probabilities x1 x2 x3
E = {eij} = { p(ot=xj|qt=si) }
The observations at continuous timesteps form an observation sequence
{o1, o2, ..., ot}, where oi ∈ {x1, x2, ..., xo}
08/12/2010 Hidden Markov Models 30

31. 6 components of HMMs
start
• Given a specific HMM and an
observation sequence, the π1 π2 π3
corresponding sequence of states t31
t11
is generally not deterministic t12 t23
• Example: s1 t21
s2 t32
s3
Given the observation sequence: e13
e11 e23 e33
{x1, x3, x3, x2} e31
e22
The corresponding states can be
any of following sequences:
x1 x2 x3
{s1, s1, s2, s2}
{s1, s2, s3, s2}
{s1, s1, s1, s2}
...
08/12/2010 Hidden Markov Models 31

32. Here’s an HMM
0.2
0.5
0.5 0.6
s1 0.4
s2 0.8
s3
0.3 0.7 0.9 0.8
0.2 0.1
x1 x2 x3
T s1 s2 s3 E x1 x2 x3 π s1 s2 s3
s1 0.5 0.5 0 s1 0.3 0 0.7 0.3 0.3 0.4
s2 0.4 0 0.6 s2 0 0.1 0.9
s3 0.2 0.8 0 s3 0.2 0 0.8
08/12/2010 Hidden Markov Models 32

33. Here’s a HMM
0.2
0.5 • Start randomly in state 1, 2
0.5 0.6
s1 s2 s3 or 3.
0.4 0.8
• Choose a output at each
0.3 0.7 0.9 state in random.
0.2 0.8
0.1 • Let’s generate a sequence
of observations:
x1 x2 x3
0.3 - 0.3 - 0.4
π s1 s2 s3 randomply choice
between S1, S2, S3
0.3 0.3 0.4
T s1 s2 s3 E x1 x2 x3
s1 0.5 0.5 0 s1 0.3 0 0.7 q1 o1
s2 0.4 0 0.6 s2 0 0.1 0.9 q2 o2
s3 0.2 0.8 0 s3 0.2 0 0.8 q3 o3
08/12/2010 Hidden Markov Models 33

34. Here’s a HMM
0.2
0.5 • Start randomly in state 1, 2
0.5 0.6
s1 s2 s3 or 3.
0.4 0.8
• Choose a output at each
0.3 0.7 0.9 state in random.
0.2 0.8
0.1 • Let’s generate a sequence
of observations:
x1 x2 x3
0.2 - 0.8
π s1 s2 s3 choice between X1
and X3
0.3 0.3 0.4
T s1 s2 s3 E x1 x2 x3
s1 0.5 0.5 0 s1 0.3 0 0.7 q1 S3 o1
s2 0.4 0 0.6 s2 0 0.1 0.9 q2 o2
s3 0.2 0.8 0 s3 0.2 0 0.8 q3 o3
08/12/2010 Hidden Markov Models 34

35. Here’s a HMM
0.2
0.5 • Start randomly in state 1, 2
0.5 0.6
s1 s2 s3 or 3.
0.4 0.8
• Choose a output at each
0.3 0.7 0.9 state in random.
0.2 0.8
0.1 • Let’s generate a sequence
of observations:
x1 x2 x3
Go to S2 with
π s1 s2 s3 probability 0.8 or
S1 with prob. 0.2
0.3 0.3 0.4
T s1 s2 s3 E x1 x2 x3
s1 0.5 0.5 0 s1 0.3 0 0.7 q1 S3 o1 X3
s2 0.4 0 0.6 s2 0 0.1 0.9 q2 o2
s3 0.2 0.8 0 s3 0.2 0 0.8 q3 o3
08/12/2010 Hidden Markov Models 35

36. Here’s a HMM
0.2
0.5 • Start randomly in state 1, 2
0.5 0.6
s1 s2 s3 or 3.
0.4 0.8
• Choose a output at each
0.3 0.7 0.9 state in random.
0.2 0.8
0.1 • Let’s generate a sequence
of observations:
x1 x2 x3
0.3 - 0.7
π s1 s2 s3 choice between X1
and X3
0.3 0.3 0.4
T s1 s2 s3 E x1 x2 x3
s1 0.5 0.5 0 s1 0.3 0 0.7 q1 S3 o1 X3
s2 0.4 0 0.6 s2 0 0.1 0.9 q2 S1 o2
s3 0.2 0.8 0 s3 0.2 0 0.8 q3 o3
08/12/2010 Hidden Markov Models 36

37. Here’s a HMM
0.2
0.5 • Start randomly in state 1, 2
0.5 0.6
s1 s2 s3 or 3.
0.4 0.8
• Choose a output at each
0.3 0.7 0.9 state in random.
0.2 0.8
0.1 • Let’s generate a sequence
of observations:
x1 x2 x3
Go to S2 with
π s1 s2 s3 probability 0.5 or
S1 with prob. 0.5
0.3 0.3 0.4
T s1 s2 s3 E x1 x2 x3
s1 0.5 0.5 0 s1 0.3 0 0.7 q1 S3 o1 X3
s2 0.4 0 0.6 s2 0 0.1 0.9 q2 S1 o2 X1
s3 0.2 0.8 0 s3 0.2 0 0.8 q3 o3
08/12/2010 Hidden Markov Models 37

38. Here’s a HMM
0.2
0.5 • Start randomly in state 1, 2
0.5 0.6
s1 s2 s3 or 3.
0.4 0.8
• Choose a output at each
0.3 0.7 0.9 state in random.
0.2 0.8
0.1 • Let’s generate a sequence
of observations:
x1 x2 x3
0.3 - 0.7
π s1 s2 s3 choice between X1
and X3
0.3 0.3 0.4
T s1 s2 s3 E x1 x2 x3
s1 0.5 0.5 0 s1 0.3 0 0.7 q1 S3 o1 X3
s2 0.4 0 0.6 s2 0 0.1 0.9 q2 S1 o2 X1
s3 0.2 0.8 0 s3 0.2 0 0.8 q3 S1 o3
08/12/2010 Hidden Markov Models 38

39. Here’s a HMM
0.2
0.5 • Start randomly in state 1, 2
0.5 0.6
s1 s2 s3 or 3.
0.4 0.8
• Choose a output at each
0.3 0.7 0.9 state in random.
0.2 0.8
0.1 • Let’s generate a sequence
of observations:
x1 x2 x3
We got a sequence
of states and
π s1 s2 s3 corresponding
0.3 0.3 0.4 observations!
T s1 s2 s3 E x1 x2 x3
s1 0.5 0.5 0 s1 0.3 0 0.7 q1 S3 o1 X3
s2 0.4 0 0.6 s2 0 0.1 0.9 q2 S1 o2 X1
s3 0.2 0.8 0 s3 0.2 0 0.8 q3 S1 o3 X3
08/12/2010 Hidden Markov Models 39

40. Three famous HMM tasks
• Given a HMM Φ = (T, E, π). Three famous HMM tasks are:
• Probability of an observation sequence (state estimation)
– Given: Φ, observation O = {o1, o2,..., ot}
– Goal: p(O|Φ), or equivalently p(st = Si|O)
• Most likely expaination (inference)
– Given: Φ, the observation O = {o1, o2,..., ot}
– Goal: Q* = argmaxQ p(Q|O)
• Learning the HMM
– Given: observation O = {o1, o2,..., ot} and corresponding state sequence
– Goal: estimate parameters of the HMM Φ = (T, E, π)
08/12/2010 Hidden Markov Models 40

41. Three famous HMM tasks
• Given a HMM Φ = (T, E, π). Three famous HMM tasks are:
• Probability of an observation sequence (state estimation)
– Given: Φ, observation O = {o1, o2,..., ot}
– Goal: p(O|Φ), or equivalently p(st = Si|O) Calculating the probability of
• Most likely expaination (inference) observing the sequence O over
all of possible sequences.
– Given: Φ, the observation O = {o1, o2,..., ot}
– Goal: Q* = argmaxQ p(Q|O)
• Learning the HMM
– Given: observation O = {o1, o2,..., ot} and corresponding state sequence
– Goal: estimate parameters of the HMM Φ = (T, E, π)
08/12/2010 Hidden Markov Models 41

42. Three famous HMM tasks
• Given a HMM Φ = (T, E, π). Three famous HMM tasks are:
• Probability of an observation sequence (state estimation)
– Given: Φ, observation O = {o1, o2,..., ot}
– Goal: p(O|Φ), or equivalently p(st = Si|O) Calculating the best
• Most likely expaination (inference) corresponding state sequence,
given an observation
– Given: Φ, the observation O = {o1, o2,..., ot}
sequence.
– Goal: Q* = argmaxQ p(Q|O)
• Learning the HMM
– Given: observation O = {o1, o2,..., ot} and corresponding state sequence
– Goal: estimate parameters of the HMM Φ = (T, E, π)
08/12/2010 Hidden Markov Models 42

43. Three famous HMM tasks
• Given a HMM Φ = (T, E, π). Three famous HMM tasks are:
• Probability of an observation sequence (state estimation)
– Given: Φ, observation O = {o1, o2,..., ot}
Given an (or a set of)
– Goal: p(O|Φ), or equivalently p(st = Si|O) observation sequence and
• Most likely expaination (inference) corresponding state sequence,
– Given: Φ, the observation O = {o1, o2,..., ot} estimate the Transition matrix,
– Goal: Q* = argmaxQ p(Q|O) Emission matrix and initial
probabilities of the HMM
• Learning the HMM
– Given: observation O = {o1, o2,..., ot} and corresponding state sequence
– Goal: estimate parameters of the HMM Φ = (T, E, π)
08/12/2010 Hidden Markov Models 43

44. Three famous HMM tasks
Problem Algorithm Complexity
State estimation Forward-Backward O(TN2)
Calculating: p(O|Φ)
Inference Viterbi decoding O(TN2)
Calculating: Q*= argmaxQp(Q|O)
Learning Baum-Welch (EM) O(TN2)
Calculating: Φ* = argmaxΦp(O|Φ)
T: number of timesteps
N: number of states
08/12/2010 Hidden Markov Models 44

45. The Forward-Backward Algorithm
• Given: Φ = (T, E, π), observation O = {o1, o2,..., ot}
• Goal: What is p(o1o2...ot)
• We can do this in a slow, stupid way
– As shown in the next slide...
08/12/2010 Hidden Markov Models 45

46. Here’s a HMM
0.5 0.2
0.5 0.6 • What is p(O) = p(o1o2o3)
s1 0.4
s2 0.8
s3 = p(o1=X3 ∧ o2=X1 ∧ o3=X3)?
0.3 0.7 0.9 • Slow, stupid way:
0.2 0.8
0.1
p (O ) = ∑ p ( OQ )
x1 x2 x3 Q∈paths of length 3
= ∑ p (O | Q ) p (Q )
Q∈paths of length 3
Q∈
• How to compute p(Q) for an
arbitrary path Q?
• How to compute p(O|Q) for an
arbitrary path Q?
08/12/2010 Hidden Markov Models 46

47. Here’s a HMM
0.5 0.2
0.5 0.6 • What is p(O) = p(o1o2o3)
s1 0.4
s2 0.8
s3 = p(o1=X3 ∧ o2=X1 ∧ o3=X3)?
0.3 0.7 0.9 • Slow, stupid way:
0.2 0.8
0.1
p (O ) = ∑ p ( OQ )
x1 x2 x3 Q∈paths of length 3
π s1 s2 s3 = ∑ p (O | Q ) p (Q )
Q∈paths of length 3
Q∈
0.3 0.3 0.4
p(Q) = p(q1q2q3) • How to compute p(Q) for an
= p(q1)p(q2|q1)p(q3|q2,q1) (chain) arbitrary path Q?
= p(q1)p(q2|q1)p(q3|q2) (why?) • How to compute p(O|Q) for an
arbitrary path Q?
Example in the case Q=S3S1S1
P(Q) = 0.4 * 0.2 * 0.5 = 0.04
08/12/2010 Hidden Markov Models 47

48. Here’s a HMM
0.5 0.2
0.5 0.6 • What is p(O) = p(o1o2o3)
s1 0.4
s2 0.8
s3 = p(o1=X3 ∧ o2=X1 ∧ o3=X3)?
0.3 0.7 0.9 • Slow, stupid way:
0.2 0.8
0.1
p (O ) = ∑ p ( OQ )
x1 x2 x3 Q∈paths of length 3
π s1 s2 s3 = ∑ p (O | Q ) p (Q )
Q∈paths of length 3
Q∈
0.3 0.3 0.4
p(O|Q) = p(o1o2o3|q1q2q3) • How to compute p(Q) for an
= p(o1|q1)p(o2|q1)p(o3|q3) (why?) arbitrary path Q?
• How to compute p(O|Q) for an
Example in the case Q=S3S1S1 arbitrary path Q?
P(O|Q) = p(X3|S3)p(X1|S1) p(X3|S1)
=0.8 * 0.3 * 0.7 = 0.168
08/12/2010 Hidden Markov Models 48

49. Here’s a HMM
0.5 0.2
0.5 0.6 • What is p(O) = p(o1o2o3)
s1 0.4
s2 0.8
s3 = p(o1=X3 ∧ o2=X1 ∧ o3=X3)?
0.3 0.7 0.9 • Slow, stupid way:
0.2 0.8
0.1
p (O ) = ∑ p ( OQ )
x1 x2 x3 Q∈paths of length 3
π s1 s2 s3 = ∑ p (O | Q ) p (Q )
Q∈paths of length 3
Q∈
0.3 0.3 0.4
p(O|Q) = p(o1o2o3|q1q2q3) • How to compute p(Q) for an
p(O) needs 27 p(Q) arbitrary path Q?
= p(o1|q1)p(o2|q1)p(o3|q3) (why?)
computations and 27
• How to compute p(O|Q) for an
p(O|Q) computations.
Example in the case Q=S3S1S1 arbitrary path Q?
P(O|Q) = p(X3|S3)p(Xsequence3has )
What if the
1|S1) p(X |S1
20 observations?
=0.8 * 0.3 * 0.7 = 0.168 So let’s be smarter...
08/12/2010 Hidden Markov Models 49

50. The Forward algorithm
• Given observation o1o2...oT
• Define:
αt(i) = p(o1o2...ot ∧ qt = Si | Φ) where 1 ≤ t ≤ T
αt(i) = probability that, in a random trial:
– We’d have seen the first t observations
– We’d have ended up in Si as the t’th state visited.
• In our example, what is α2(3) ?
08/12/2010 Hidden Markov Models 50