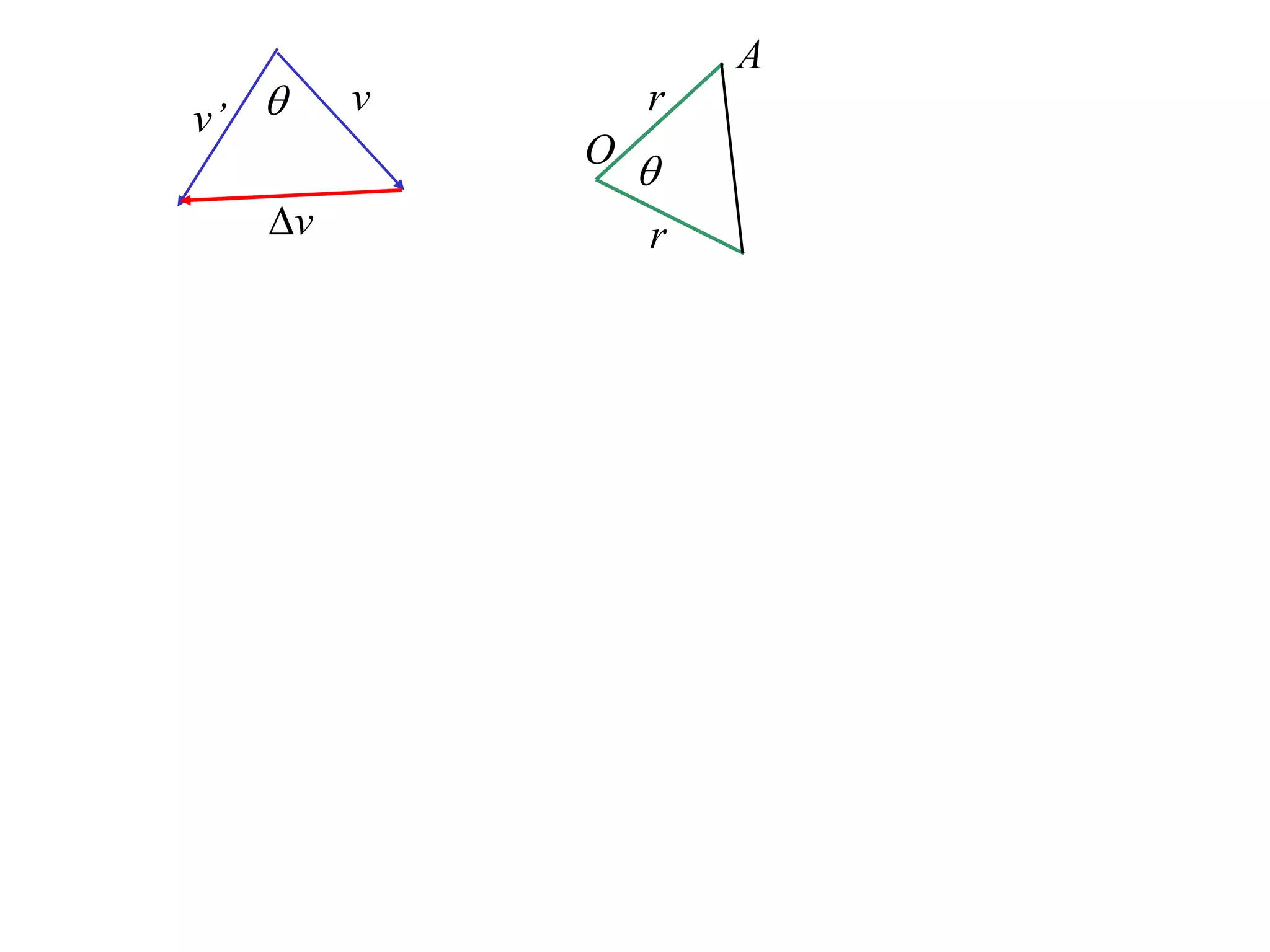
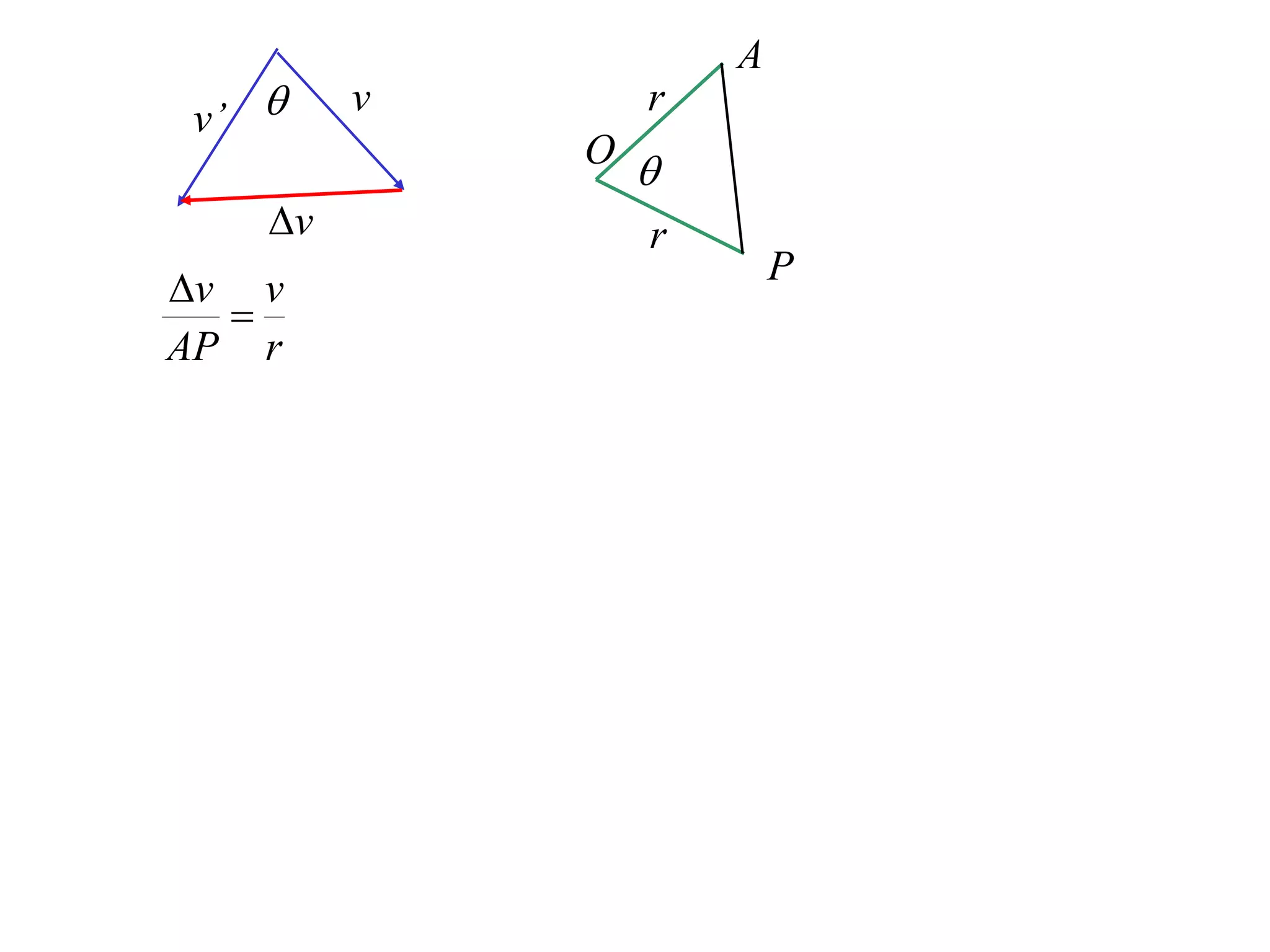
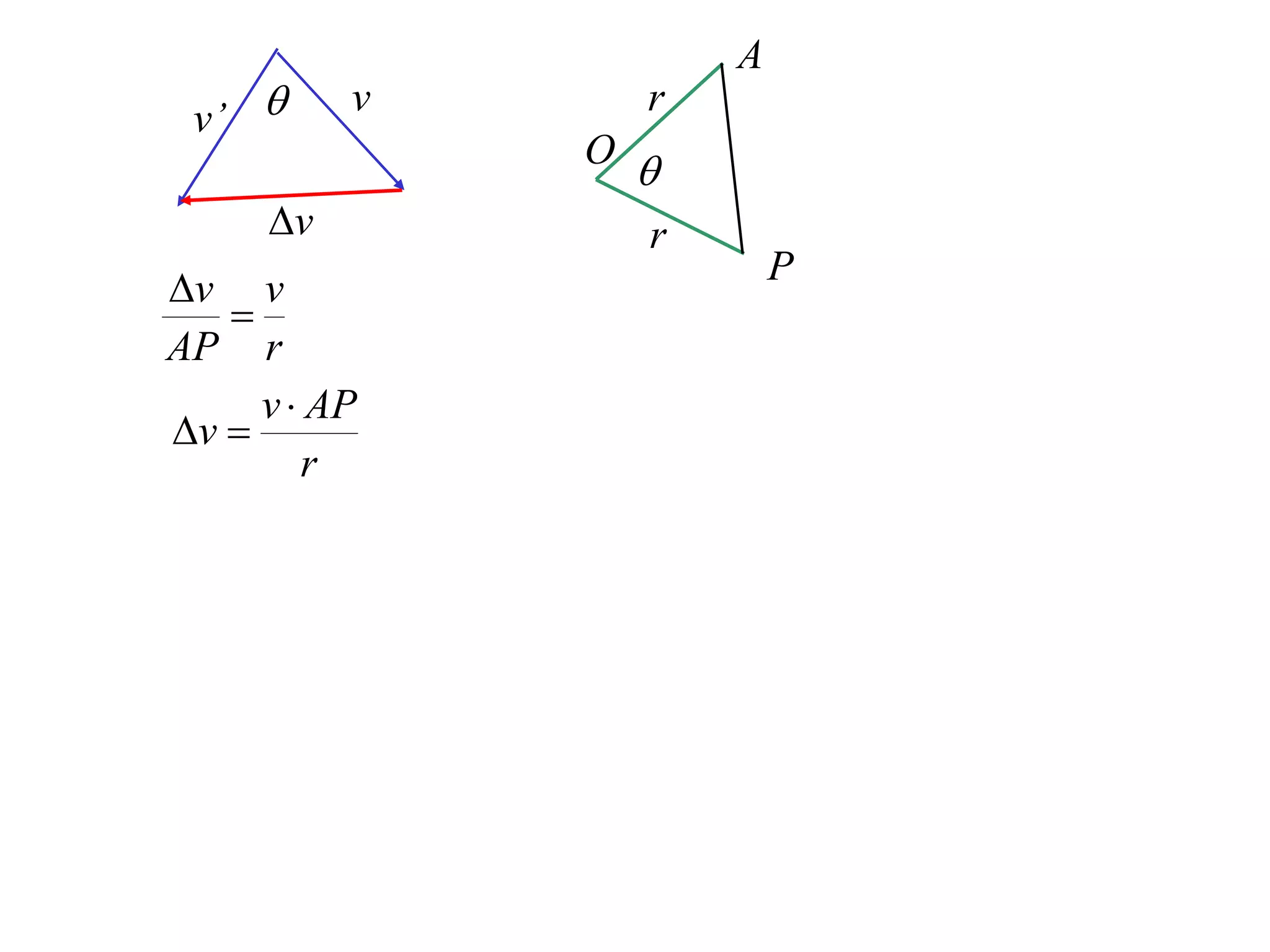
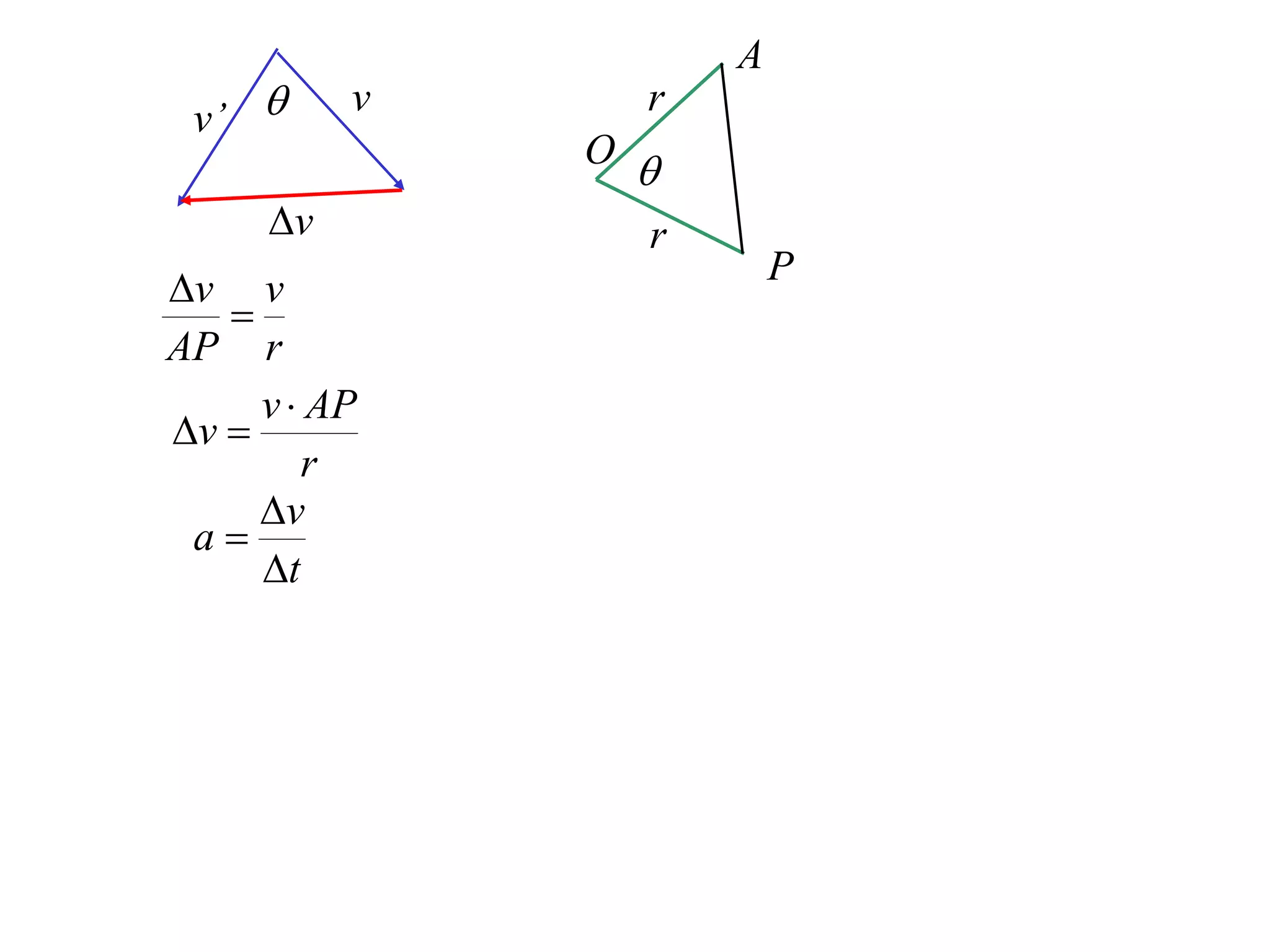
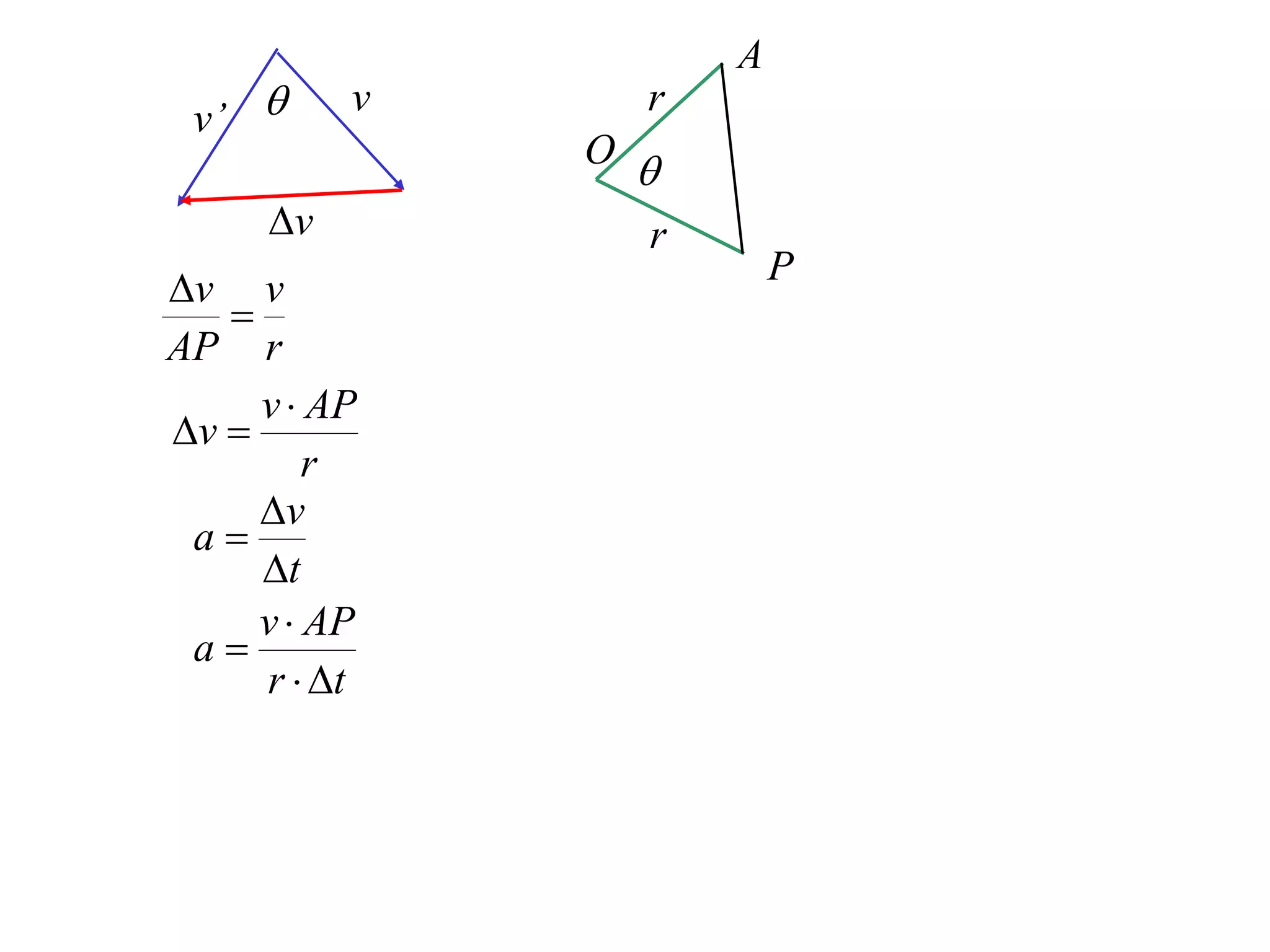
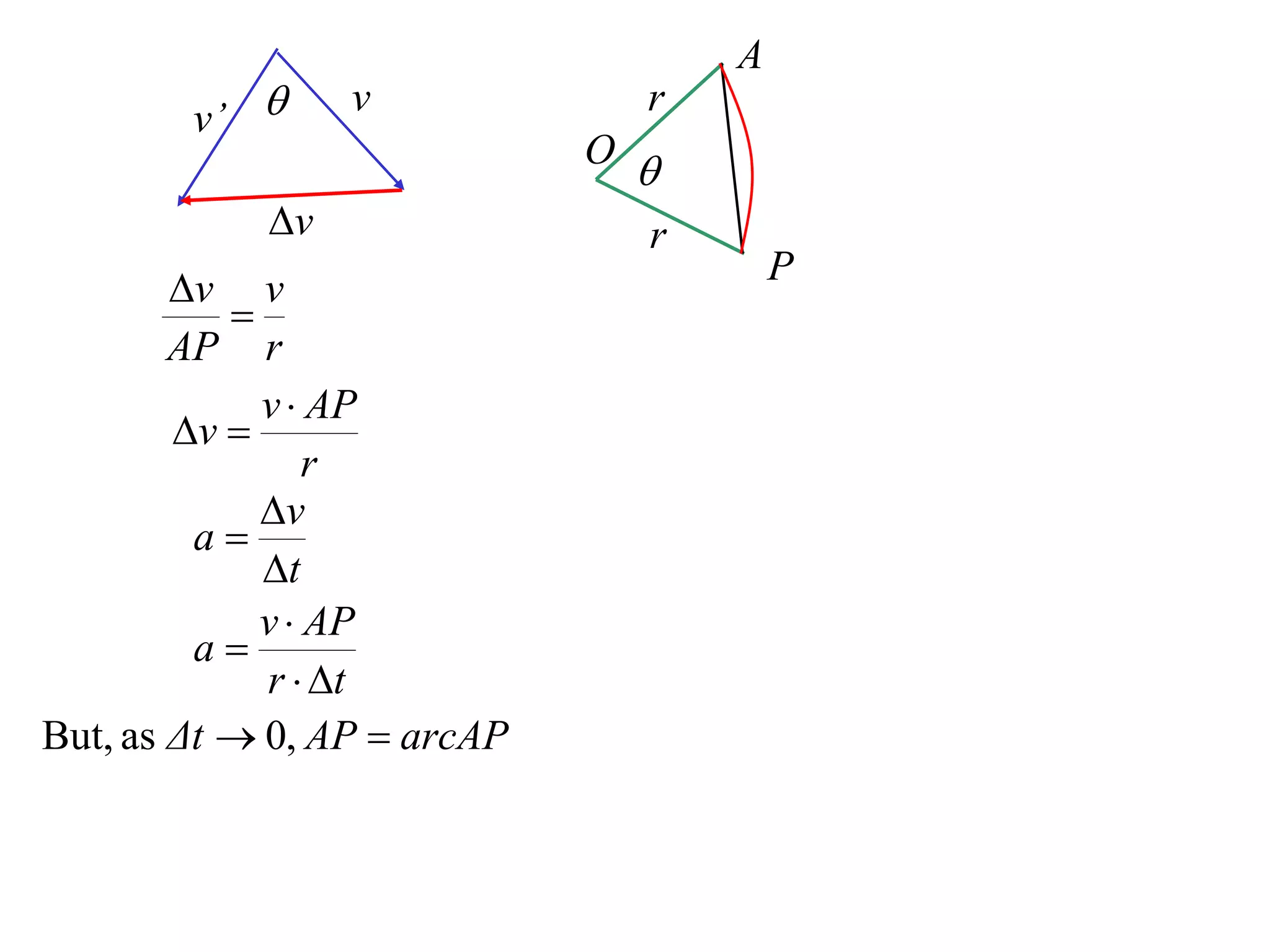
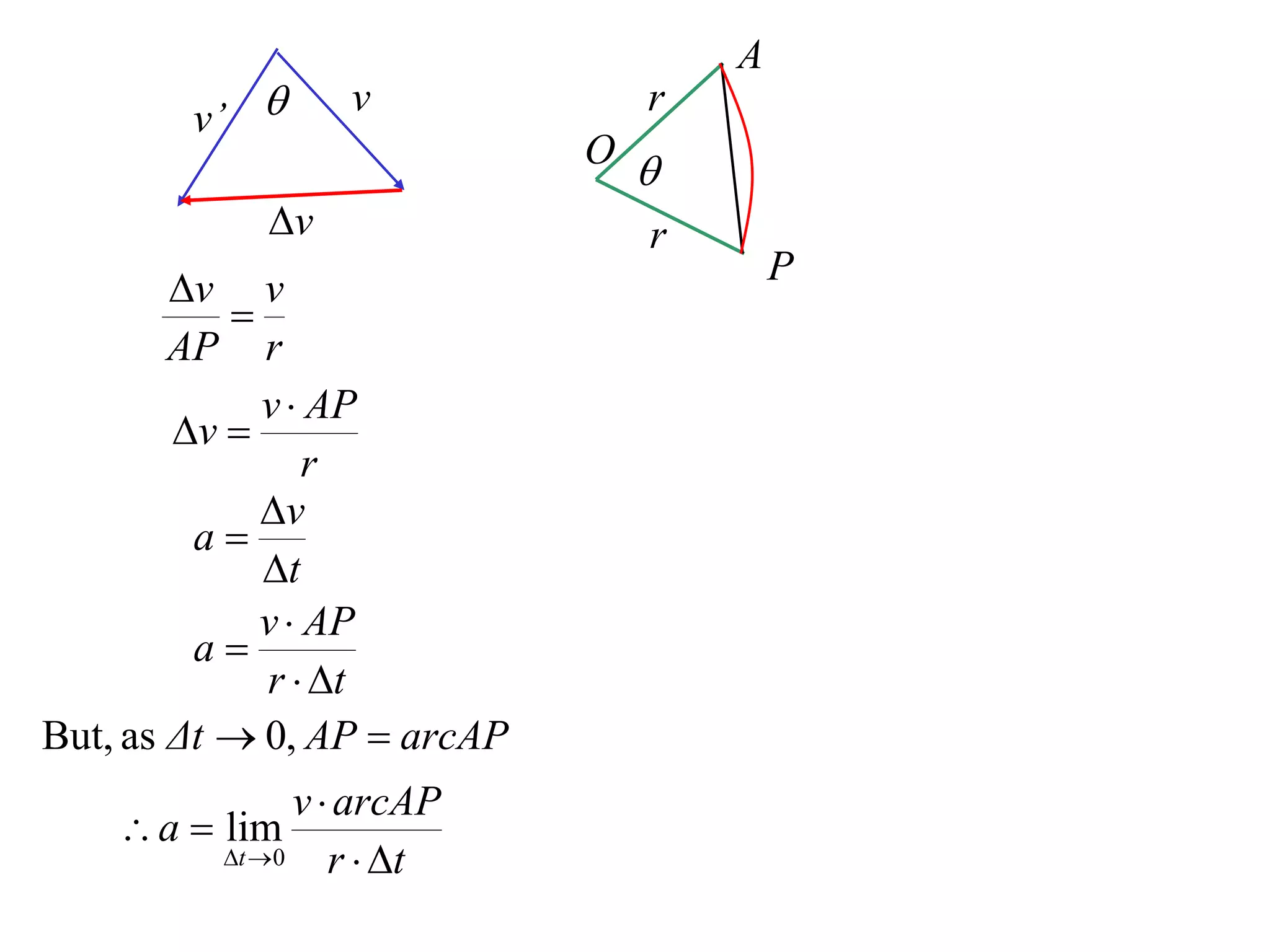
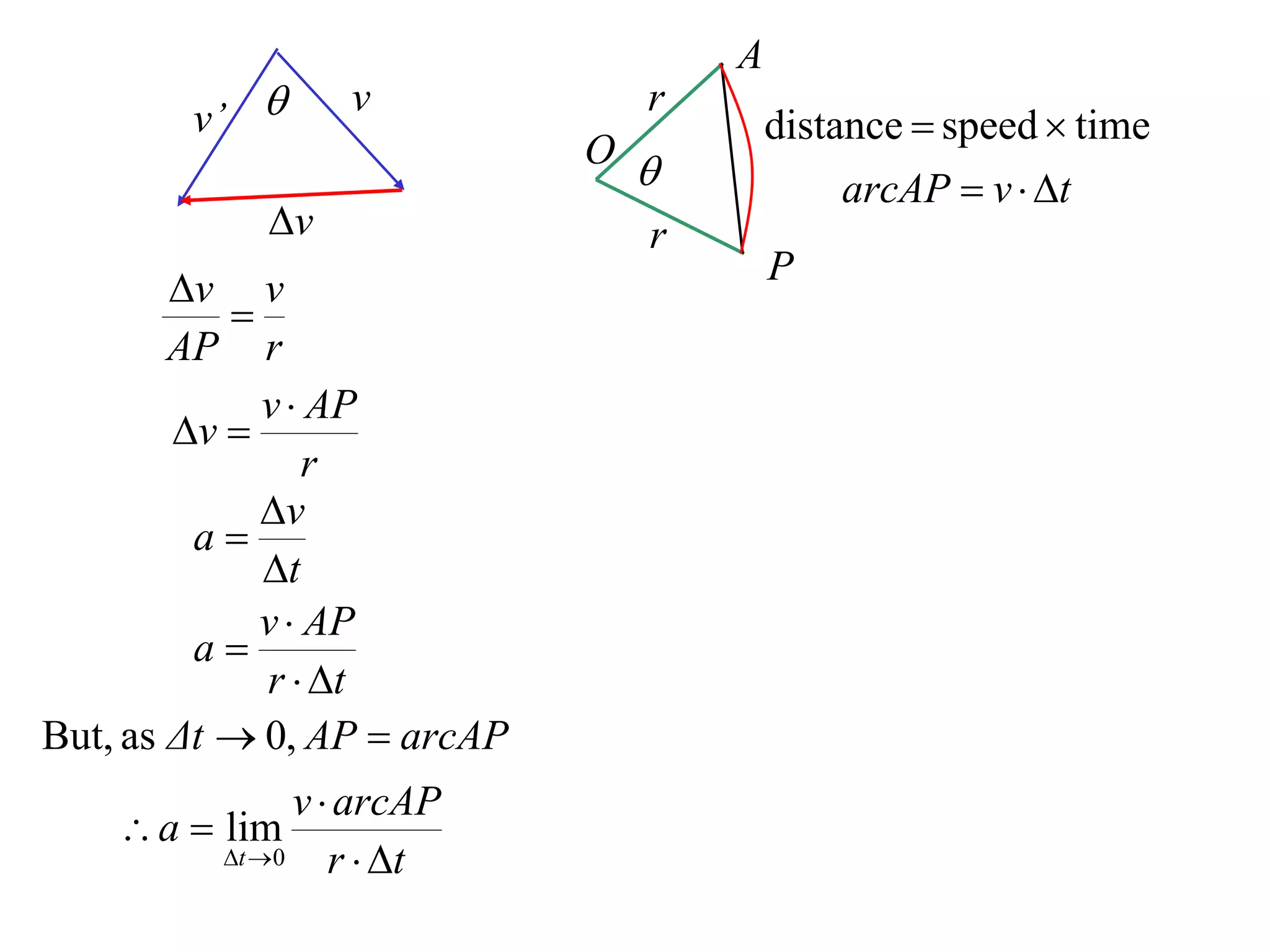
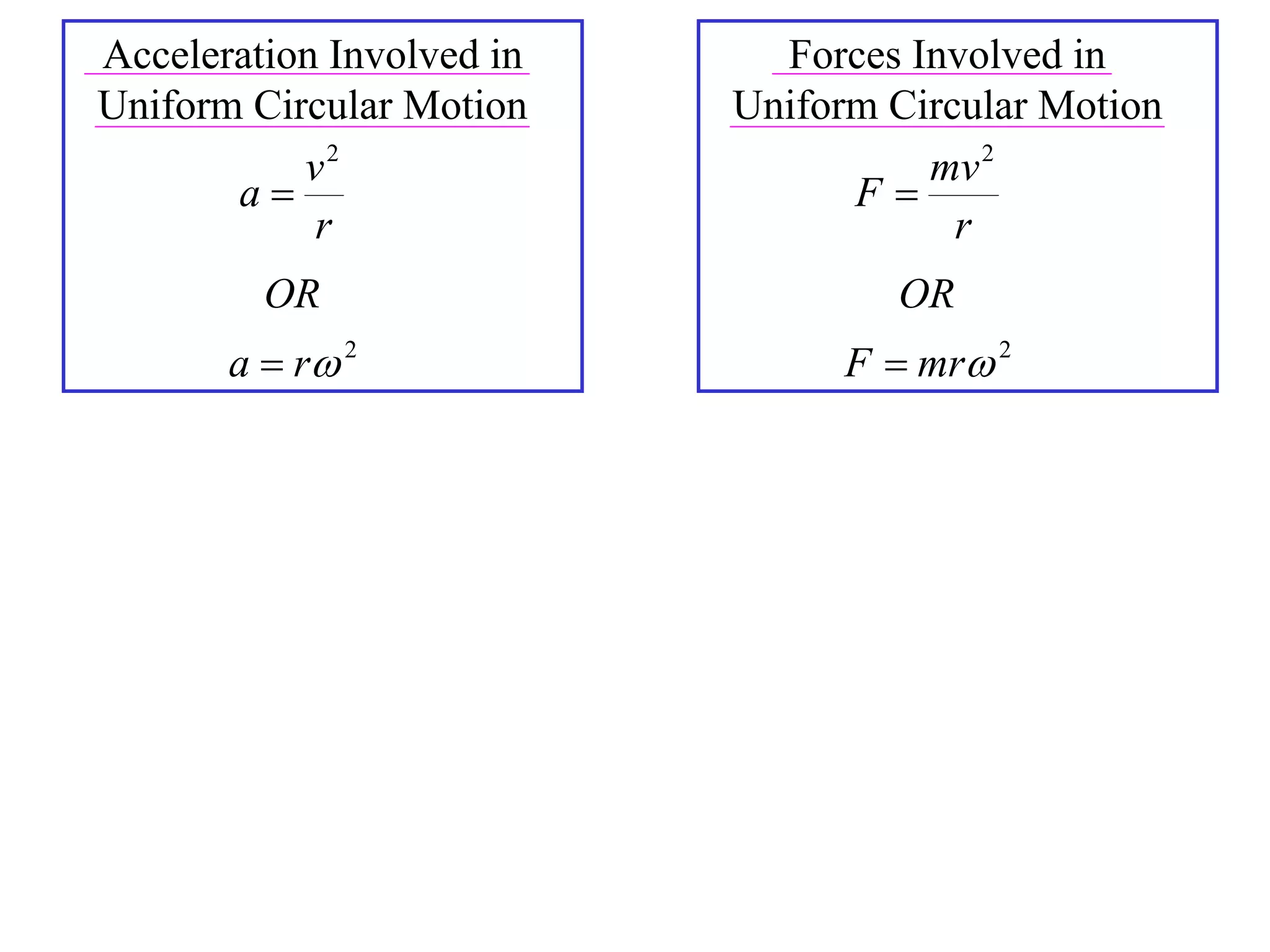
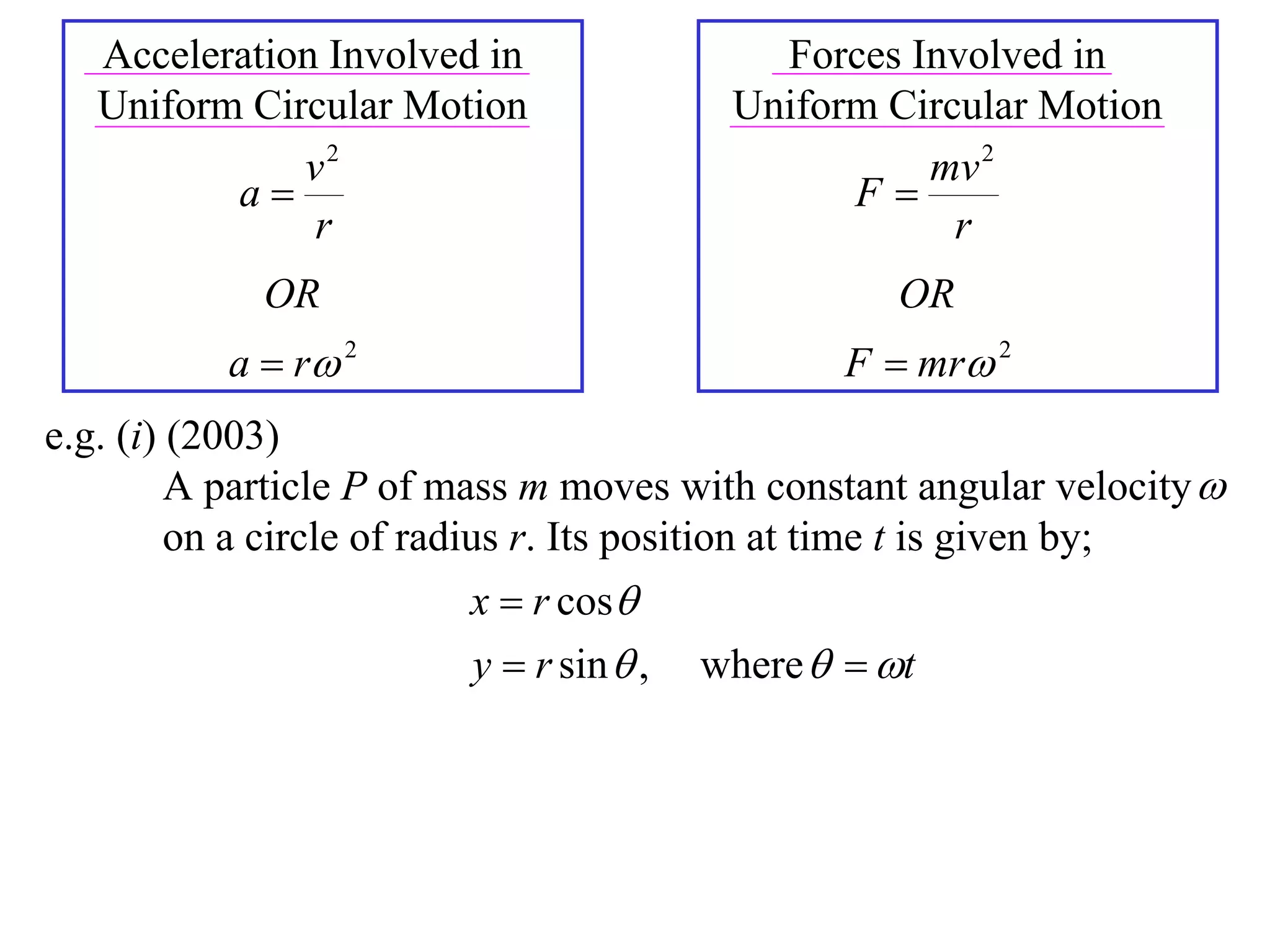
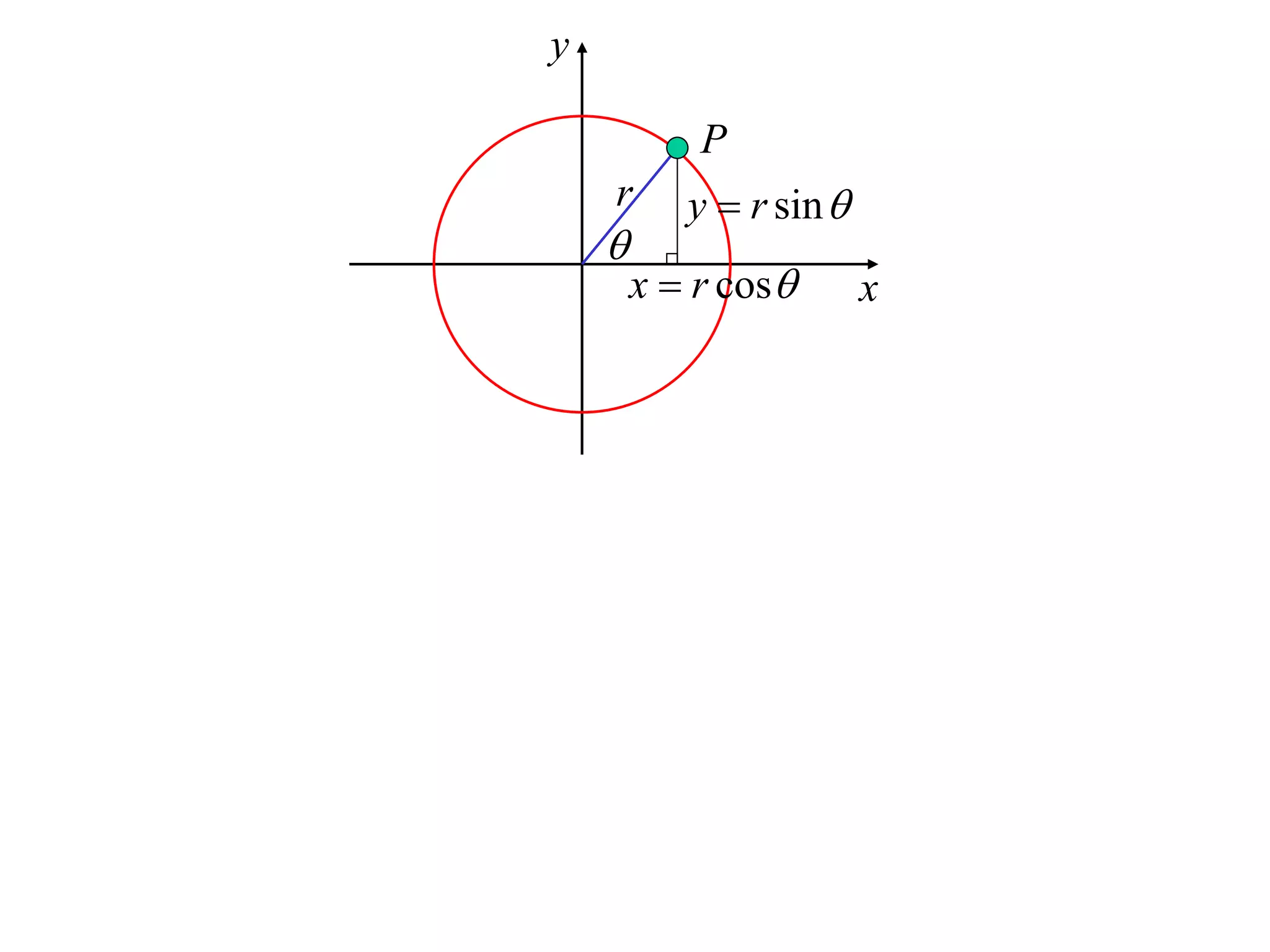
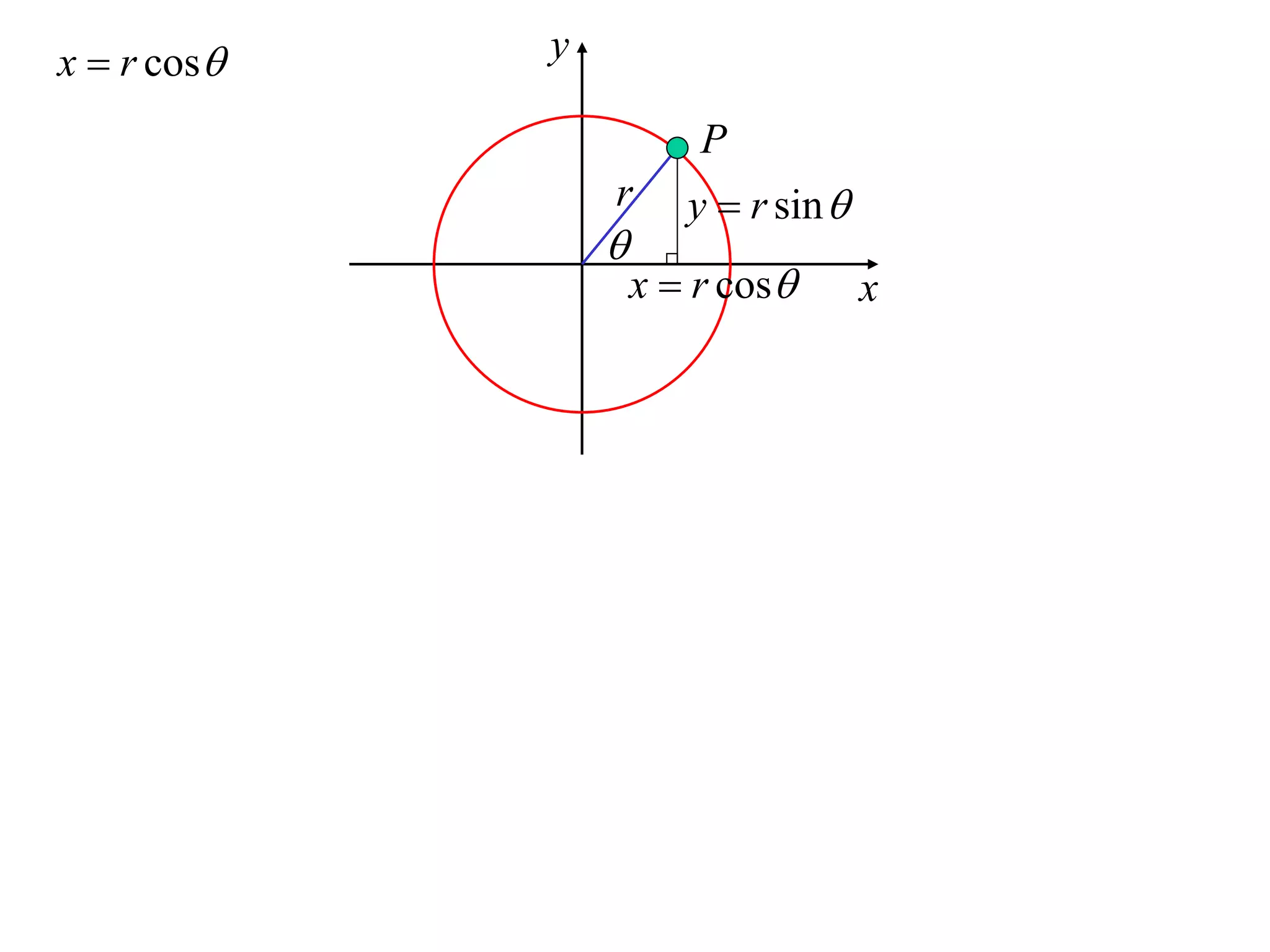
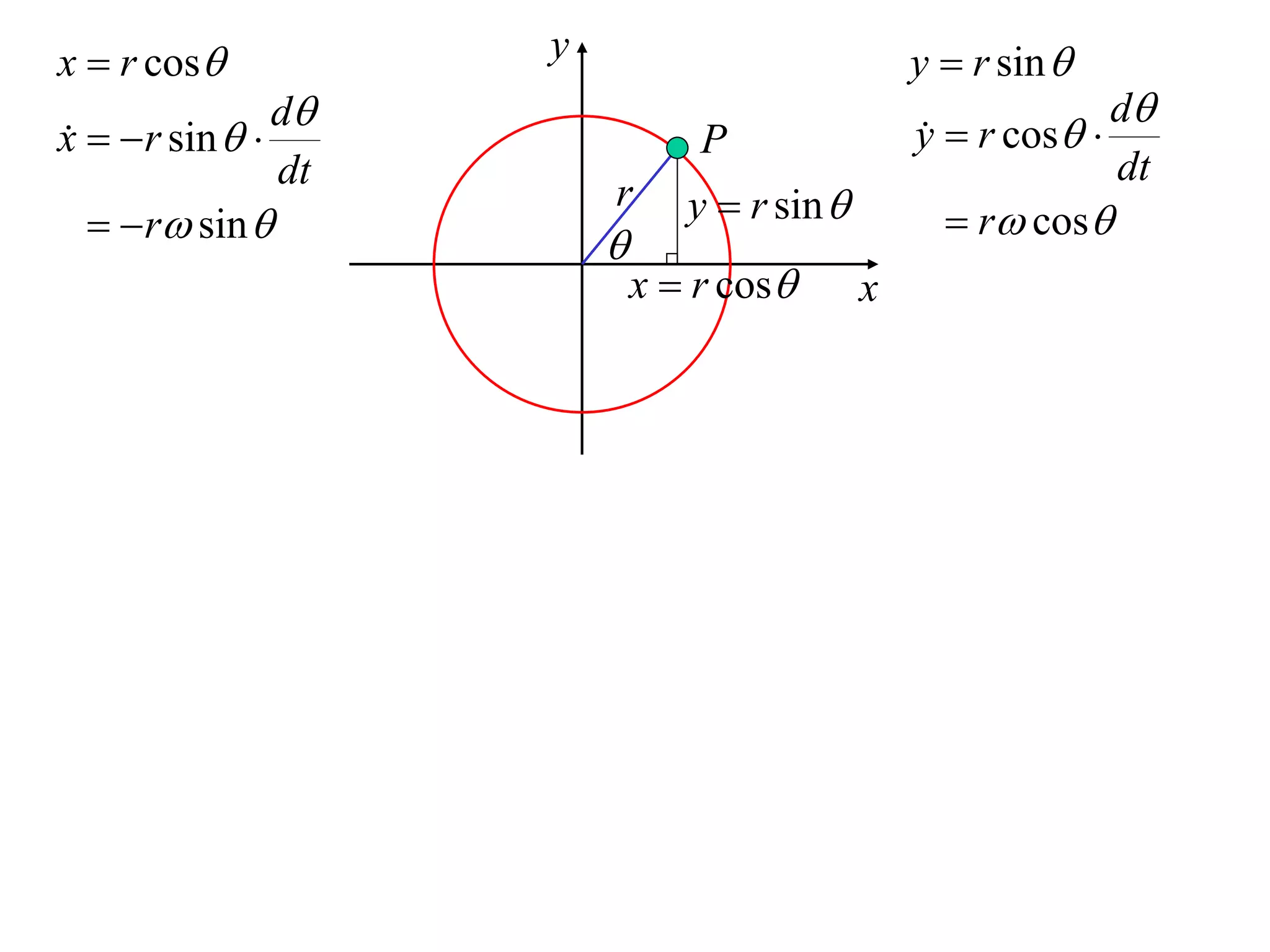
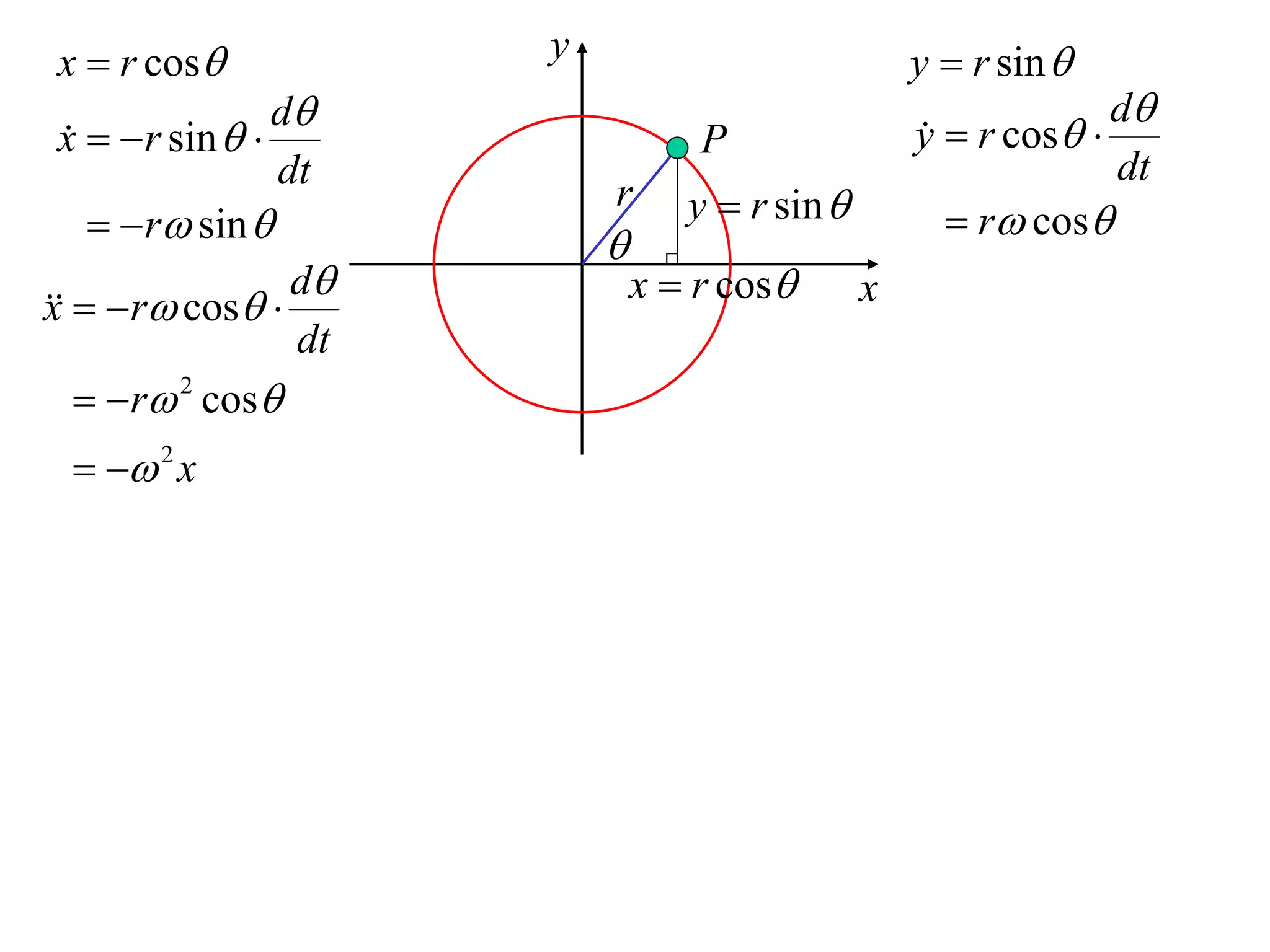
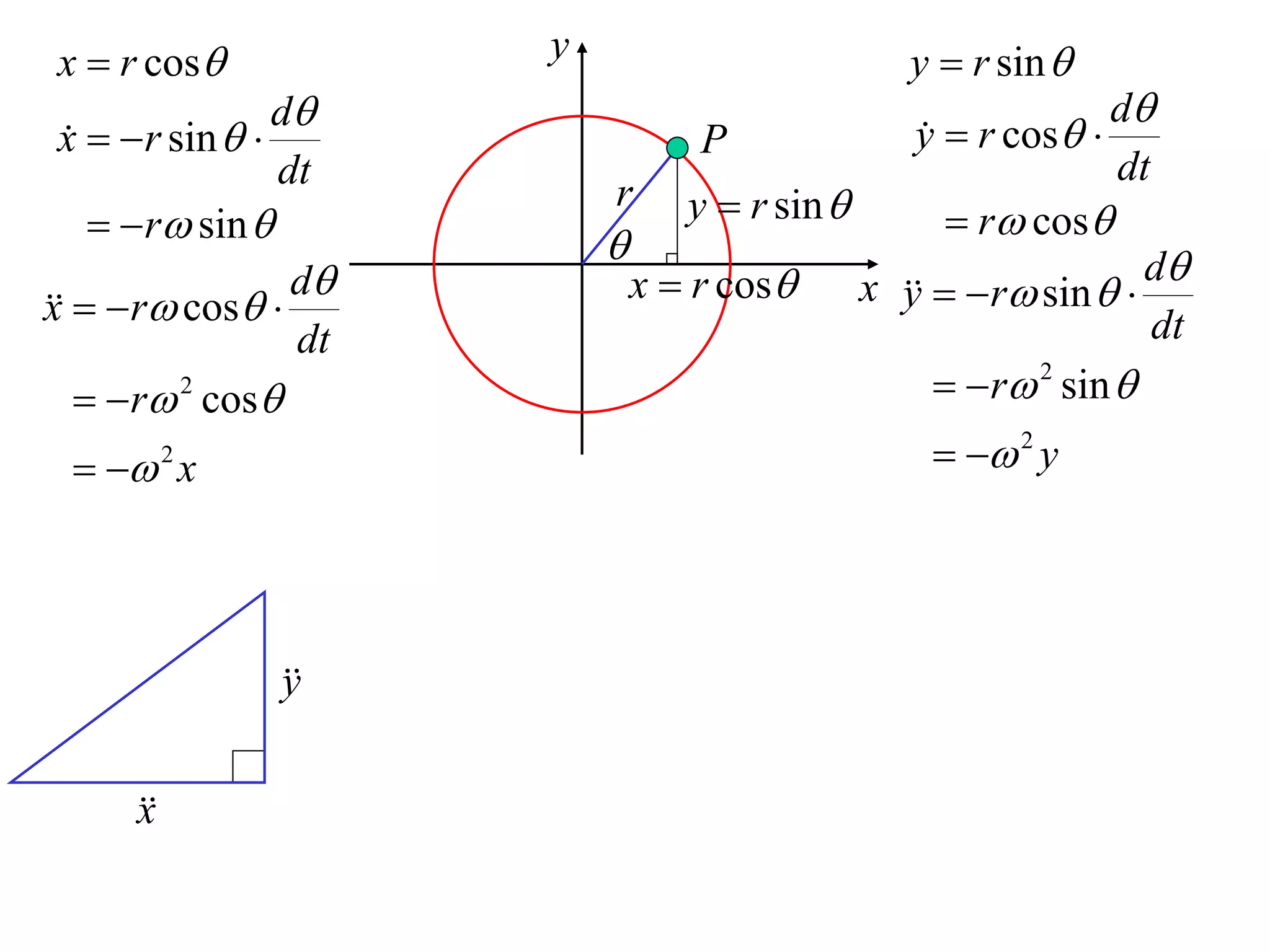
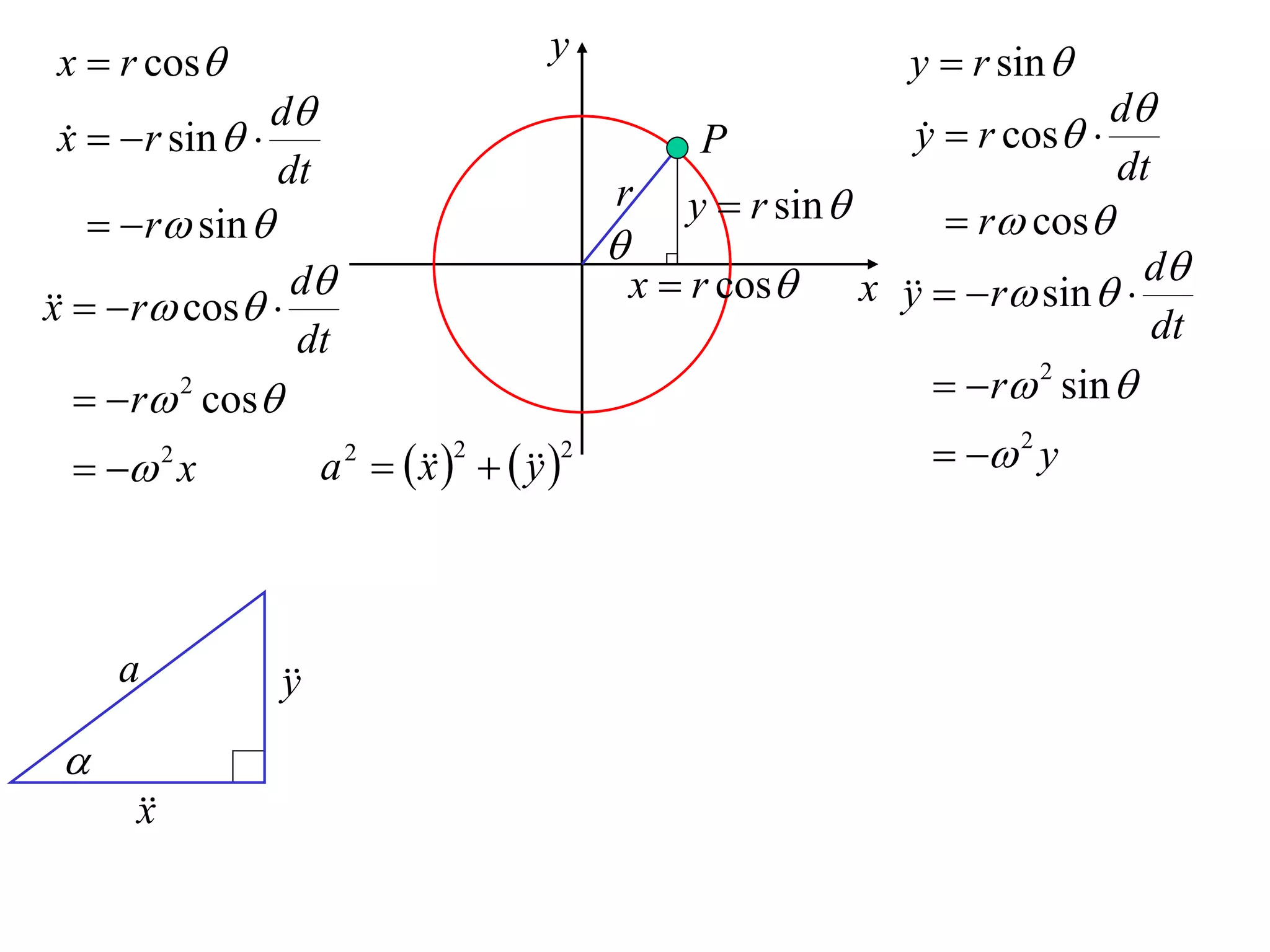
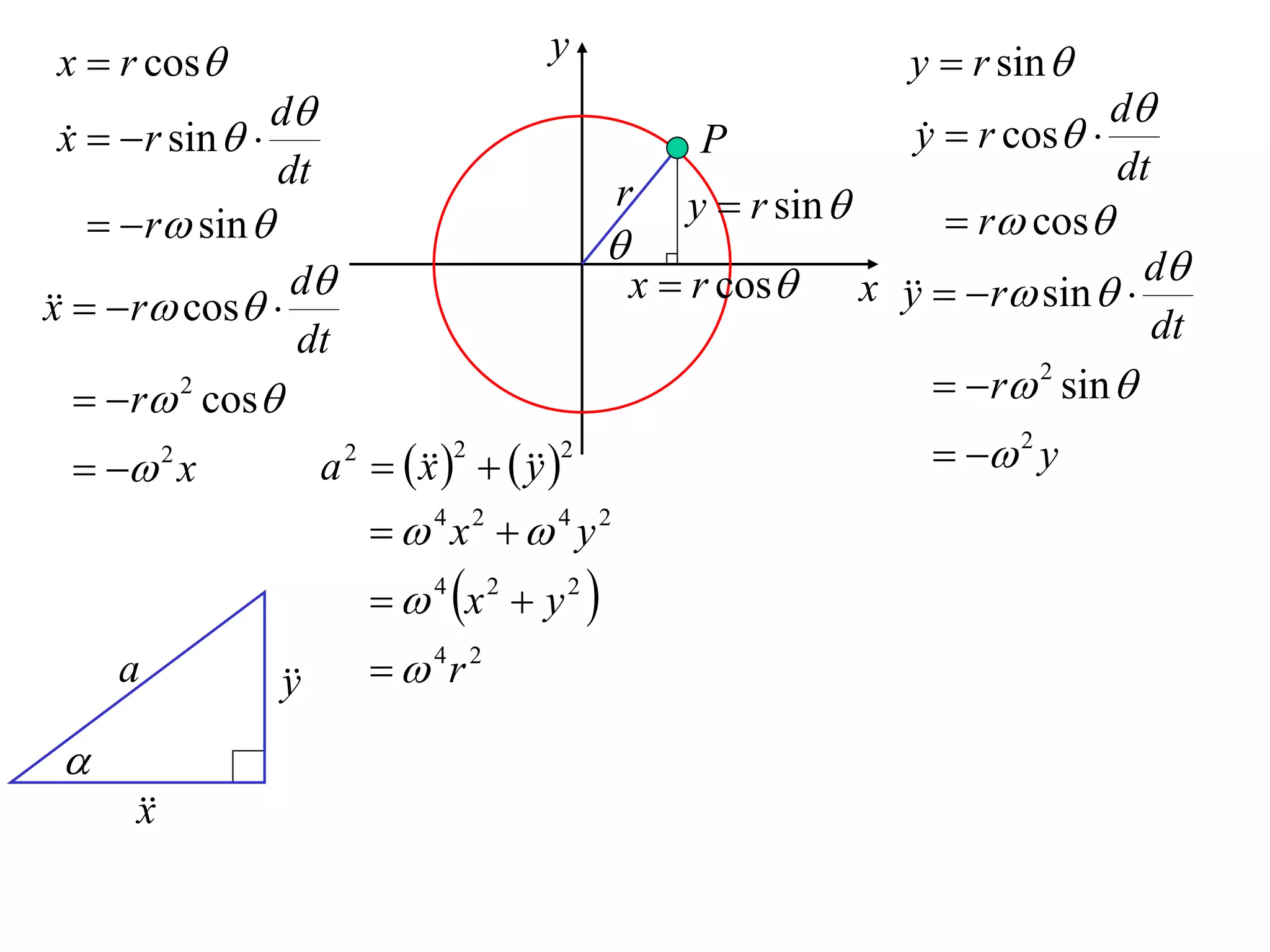
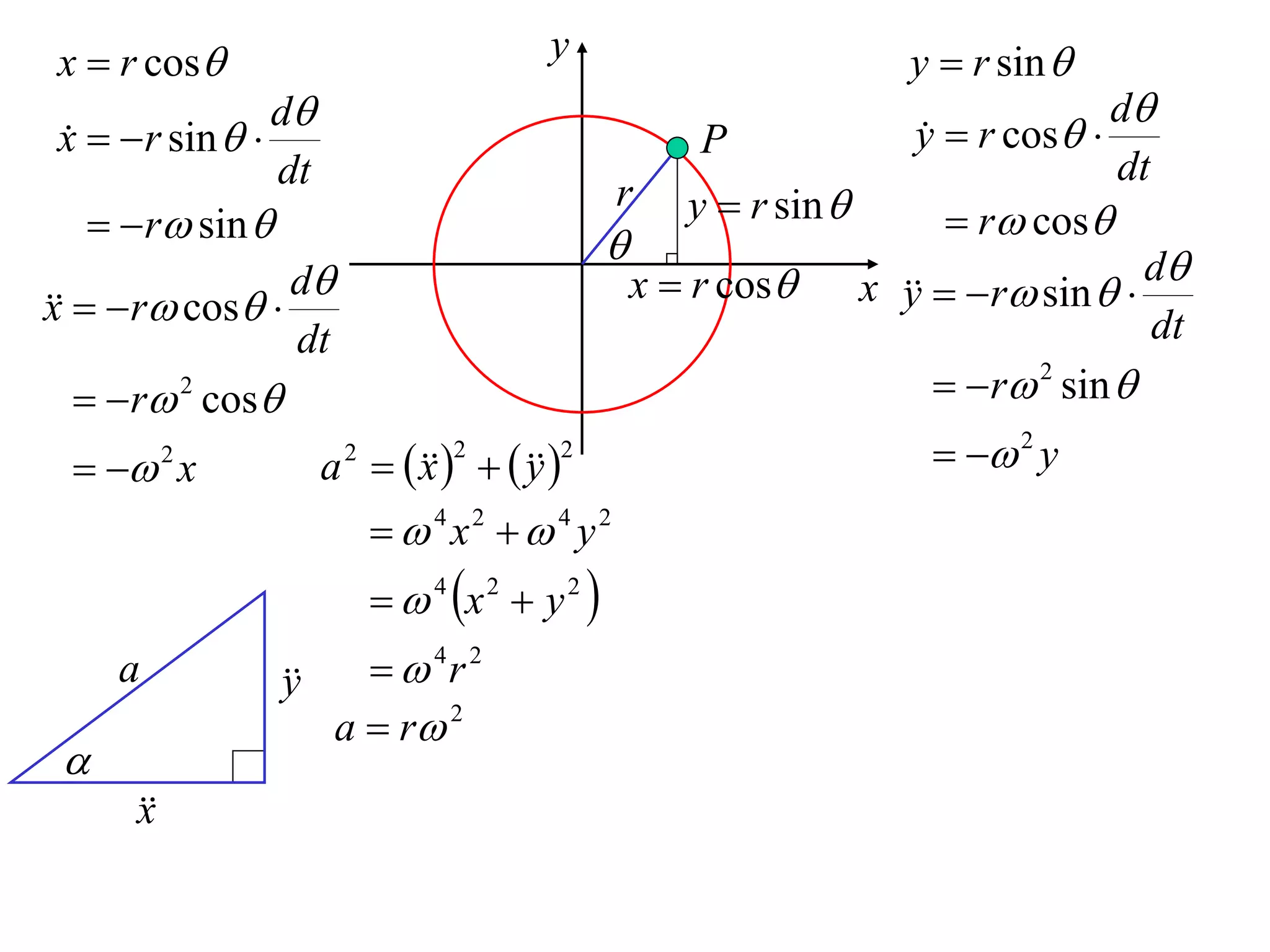
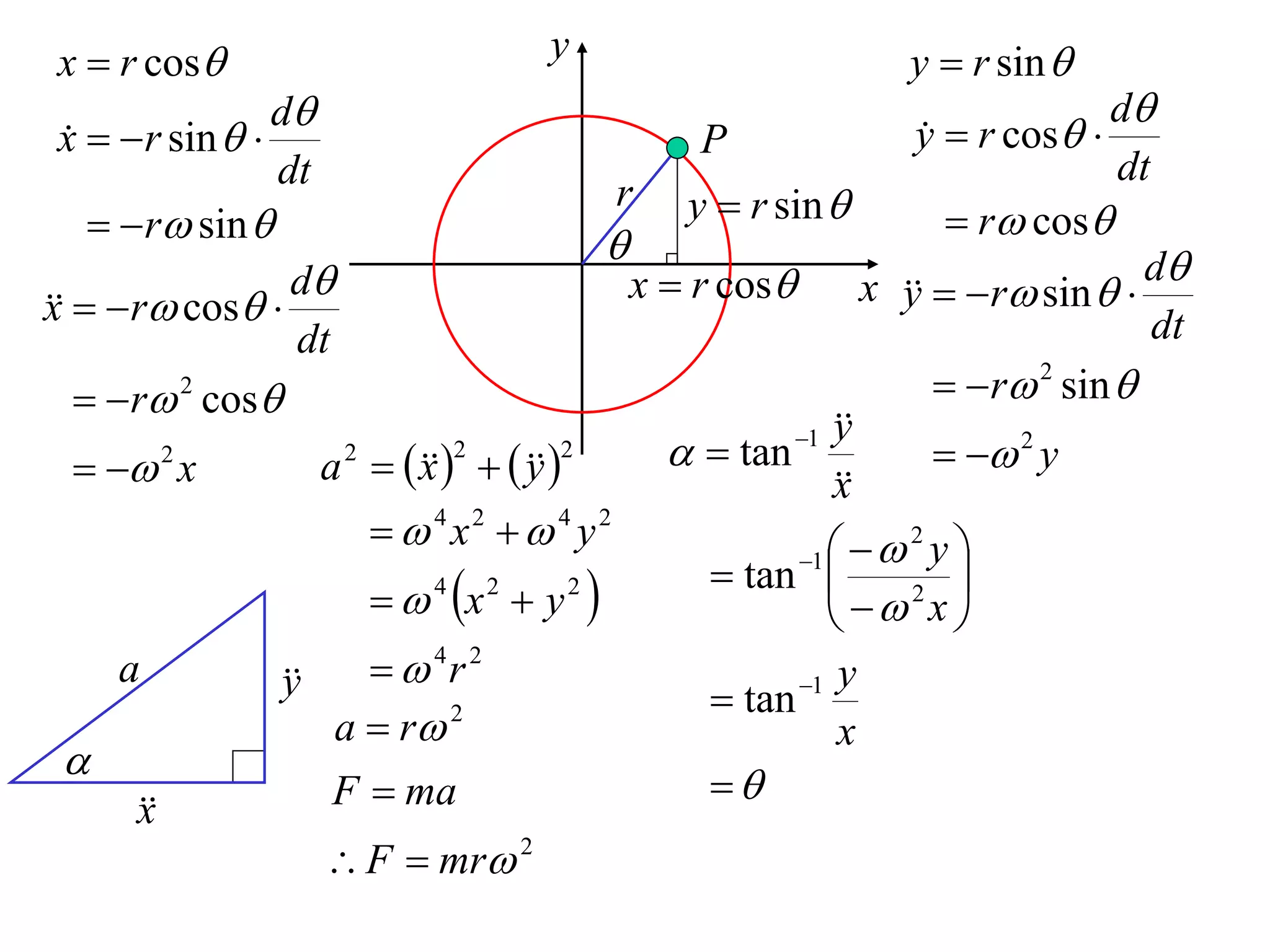
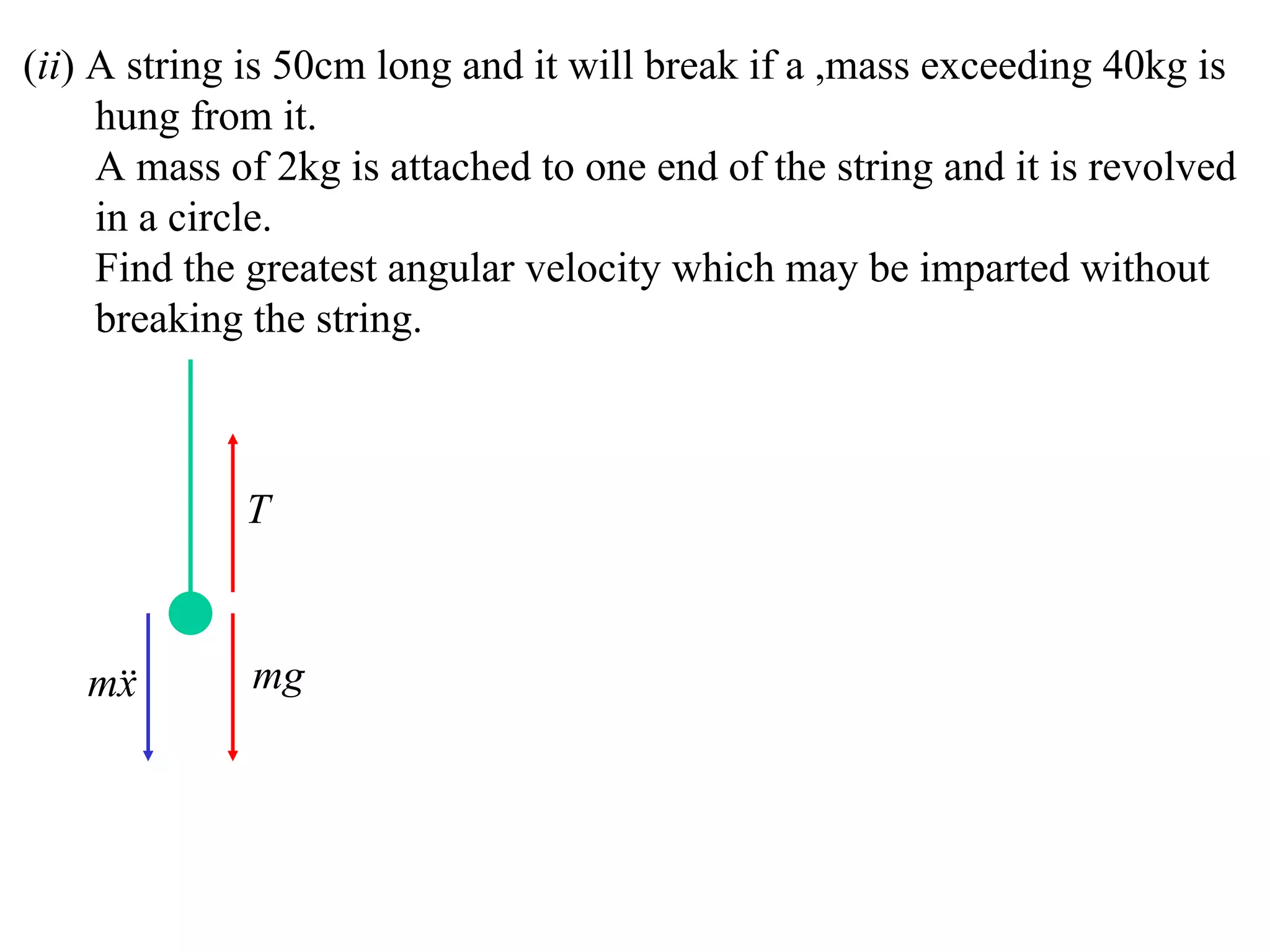
1) Uniform circular motion occurs when a particle moves with a constant angular velocity, meaning its linear velocity also remains constant. 2) For an object moving in uniform circular motion, its acceleration is calculated as the change in velocity over time. 3) This acceleration can be shown to equal v^2/r, where v is the object's linear velocity and r is the radius of its circular path.

1. Acceleration with Uniform
Circular Motion

2. Acceleration with Uniform
Circular Motion
Uniform circular motion is when a particle moves with constant angular
velocity.

3. Acceleration with Uniform
Circular Motion
Uniform circular motion is when a particle moves with constant angular
velocity.  the magnitude of the linear velocity will also be constant 

4. Acceleration with Uniform
Circular Motion
Uniform circular motion is when a particle moves with constant angular
velocity.  the magnitude of the linear velocity will also be constant 
A
r
O

5. Acceleration with Uniform
Circular Motion
Uniform circular motion is when a particle moves with constant angular
velocity.  the magnitude of the linear velocity will also be constant 
A particle moves from A to P with constant
A
angular velocity.
r
O

P

6. Acceleration with Uniform
Circular Motion
Uniform circular motion is when a particle moves with constant angular
velocity.  the magnitude of the linear velocity will also be constant 
A particle moves from A to P with constant
A
angular velocity.
r
O
 The acceleration of the particle is the change
in velocity with respect to time.
P

7. Acceleration with Uniform
Circular Motion
Uniform circular motion is when a particle moves with constant angular
velocity.  the magnitude of the linear velocity will also be constant 
A particle moves from A to P with constant
A
angular velocity.
r v
O
 The acceleration of the particle is the change
in velocity with respect to time.
P

8. Acceleration with Uniform
Circular Motion
Uniform circular motion is when a particle moves with constant angular
velocity.  the magnitude of the linear velocity will also be constant 
A particle moves from A to P with constant
A
angular velocity.
r v
O
 The acceleration of the particle is the change
in velocity with respect to time.
P
v’

9. Acceleration with Uniform
Circular Motion
Uniform circular motion is when a particle moves with constant angular
velocity.  the magnitude of the linear velocity will also be constant 
A particle moves from A to P with constant
A
angular velocity.
r v
O
 The acceleration of the particle is the change
in velocity with respect to time.
P
v’ v

10. Acceleration with Uniform
Circular Motion
Uniform circular motion is when a particle moves with constant angular
velocity.  the magnitude of the linear velocity will also be constant 
A particle moves from A to P with constant
A
angular velocity.
r v
O
 The acceleration of the particle is the change
in velocity with respect to time.
P
v’ v
v’

11. Acceleration with Uniform
Circular Motion
Uniform circular motion is when a particle moves with constant angular
velocity.  the magnitude of the linear velocity will also be constant 
A particle moves from A to P with constant
A
angular velocity.
r v
O
 The acceleration of the particle is the change
in velocity with respect to time.
P
v’ v
v’
v

12. Acceleration with Uniform
Circular Motion
Uniform circular motion is when a particle moves with constant angular
velocity.  the magnitude of the linear velocity will also be constant 
A A particle moves from A to P with constant
angular velocity.
r v
O
 The acceleration of the particle is the change
in velocity with respect to time.
P
v’ v’  v
v

13. Acceleration with Uniform
Circular Motion
Uniform circular motion is when a particle moves with constant angular
velocity.  the magnitude of the linear velocity will also be constant 
A A particle moves from A to P with constant
angular velocity.
r v
O
 The acceleration of the particle is the change
in velocity with respect to time.
P
v’  v
v’ This triangle of vectors
is similar to OAP
v

14. A
v’ 
v r
O

v r

15. A
v’ 
v r
O

v r
P
v v

AP r

16. A
v’ 
v r
O

v r
P
v v

AP r
v  AP
v 
r

17. A
v’ 
v r
O

v r
P
v v

AP r
v  AP
v 
r
v
a
t

18. A
v’ 
v r
O

v r
P
v v

AP r
v  AP
v 
r
v
a
t
v  AP
a
r  t

19. A
v’ 
v r
O

v r
P
v v

AP r
v  AP
v 
r
v
a
t
v  AP
a
r  t
But, as Δt  0, AP  arcAP

20. A
v’ 
v r
O

v r
P
v v

AP r
v  AP
v 
r
v
a
t
v  AP
a
r  t
But, as Δt  0, AP  arcAP
v  arcAP
 a  lim
t 0 r  t

21. A
v’ 
v r
distance  speed  time
O
 arcAP  v  t
v r
P
v v

AP r
v  AP
v 
r
v
a
t
v  AP
a
r  t
But, as Δt  0, AP  arcAP
v  arcAP
 a  lim
t 0 r  t

22. A
v’  v r
distance  speed  time
O
 arcAP  v  t
v r
P
v v
 v  v  t
AP r  a  lim
t 0 r  t
v  AP
v 
r v2
 lim
v t 0 r
a
t v2

v  AP r
a
r  t
But, as Δt  0, AP  arcAP
v  arcAP
 a  lim
t 0 r  t

23. A
v’  v r
distance  speed  time
O
 arcAP  v  t
v r
P
v v
 v  v  t
AP r  a  lim
t 0 r  t
v  AP
v 
r v2
 lim
v t 0 r
a
t v2

v  AP r
a
r  t
 the acceleration in uniform circular
But, as Δt  0, AP  arcAP
v2
v  arcAP motion has magnitude and is
 a  lim r
t 0 r  t
directed towards the centre

24. Acceleration Involved in
Uniform Circular Motion
v2
a
r

25. Acceleration Involved in
Uniform Circular Motion
v2
a
r
OR
a  r 2

26. Acceleration Involved in Forces Involved in
Uniform Circular Motion Uniform Circular Motion
v2
a
r
OR
a  r 2

27. Acceleration Involved in Forces Involved in
Uniform Circular Motion Uniform Circular Motion
v2 mv 2
a F
r r
OR
a  r 2

28. Acceleration Involved in Forces Involved in
Uniform Circular Motion Uniform Circular Motion
v2 mv 2
a F
r r
OR OR
a  r 2 F  mr 2

29. Acceleration Involved in Forces Involved in
Uniform Circular Motion Uniform Circular Motion
v2 mv 2
a F
r r
OR OR
a  r 2 F  mr 2
e.g. (i) (2003)
A particle P of mass m moves with constant angular velocity 
on a circle of radius r. Its position at time t is given by;
x  r cos
y  r sin  , where   t

30. Acceleration Involved in Forces Involved in
Uniform Circular Motion Uniform Circular Motion
v2 mv 2
a F
r r
OR OR
a  r 2 F  mr 2
e.g. (i) (2003)
A particle P of mass m moves with constant angular velocity 
on a circle of radius r. Its position at time t is given by;
x  r cos
y  r sin  , where   t
a) Show that there is an inward radial force of magnitude mr 2 acting
on P.

31. y
P
r y  r sin 

x  r cos x

32. x  r cos y
P
r y  r sin 

x  r cos x

33. x  r cos y y  r sin 
P
r y  r sin 

x  r cos x

34. x  r cos y y  r sin 
d
x   r sin  
 P
dt
r y  r sin 
  r sin 

x  r cos x

35. x  r cos y y  r sin 
d d
x   r sin  
 P y  r cos 

dt dt
r y  r sin 
  r sin   r cos

x  r cos x

36. x  r cos y y  r sin 
d d
x   r sin  
 P y  r cos 

dt dt
r y  r sin 
  r sin   r cos

d x  r cos x
   r cos 
x
dt
  r 2 cos
  2 x

37. x  r cos y y  r sin 
d d
x   r sin  
 P y  r cos 

dt dt
r y  r sin 
  r sin   r cos

   r cos 
x
d x  r cos x    r sin   d
y
dt dt
  r 2 cos   r 2 sin 
  x2   2 y

38. x  r cos y y  r sin 
d d
x   r sin  
 P y  r cos 

dt dt
r y  r sin 
  r sin   r cos

   r cos 
x
d x  r cos x    r sin   d
y
dt dt
  r 2 cos   r 2 sin 
  x 2   2 y
y

x


39. x  r cos y y  r sin 
d d
x   r sin  
 P y  r cos 

dt dt
r y  r sin 
  r sin   r cos

   r cos 
x
d x  r cos x    r sin   d
y
dt dt
  r 2 cos   r 2 sin 
  x 2   2 y
a y


x


40. x  r cos y y  r sin 
d d
x   r sin  
 P y  r cos 

dt dt
r y  r sin 
  r sin   r cos

   r cos 
x
d x  r cos x    r sin   d
y
dt dt
  r 2 cos   r 2 sin 
  x 2
a     
2
x
2
y
2   2 y
a y


x


41. x  r cos y y  r sin 
d d
x   r sin  
 P y  r cos 

dt dt
r y  r sin 
  r sin   r cos

   r cos 
x
d x  r cos x    r sin   d
y
dt dt
  r 2 cos   r 2 sin 
  x 2
a     
2
x
2
y
2   2 y
  4 x2   4 y2
  4 x 2  y 2 
a y
   4r 2

x


42. x  r cos y y  r sin 
d d
x   r sin  
 P y  r cos 

dt dt
r y  r sin 
  r sin   r cos

   r cos 
x
d x  r cos x    r sin   d
y
dt dt
  r 2 cos   r 2 sin 
  x 2
a     
2
x y
2 2   2 y
  4 x2   4 y2
  4 x 2  y 2 
a y
   4r 2
a  r 2

x


43. x  r cos y y  r sin 
d d
x   r sin  
 P y  r cos 

dt dt
r y  r sin 
  r sin   r cos

   r cos 
x
d x  r cos x    r sin   d
y
dt dt
  r 2 cos   r 2 sin 
  x 2
a     
2
x y
2 2   2 y
  4 x2   4 y2
  4 x 2  y 2 
a y
   4r 2
a  r 2

x
 F  ma
 F  mr 2

44. x  r cos y y  r sin 
d d
x   r sin  
 P y  r cos 

dt dt
r y  r sin 
  r sin   r cos

   r cos 
x
d x  r cos x    r sin   d
y
dt dt
  r 2 cos   r 2 sin 
y

  x 2
a     
2
x y
2 2   tan 1   2 y
x

  4 x2   4 y2
  4 x 2  y 2 
a y
   4r 2
a  r 2

x
 F  ma
 F  mr 2

45. x  r cos y y  r sin 
d d
x   r sin  
 P y  r cos 

dt dt
r y  r sin 
  r sin   r cos

   r cos 
x
d x  r cos x    r sin   d
y
dt dt
  r 2 cos   r 2 sin 
y

  x 2
a     
2
x y
2 2   tan 1   2 y
x

  4 x2   4 y2   2 y 
 tan 1  
  4 x 2  y 2    x 
2
a y
   4r 2 y
 tan 1
a  r 2 x

F  ma 
x

 F  mr 2

46. x  r cos y y  r sin 
d d
x   r sin  
 P y  r cos 

dt dt
r y  r sin 
  r sin   r cos

   r cos 
x
d x  r cos x    r sin   d
y
dt dt
  r 2 cos   r 2 sin 
y

  x 2
a     
2
x y
2 2   tan 1   2 y
x

  4 x2   4 y2   2 y 
 tan 1  
  4 x 2  y 2    x 
2
a y
   4r 2 y
 tan 1
a  r 2 x

F  ma 
x

 F  mr 2  There is a force , F  mr 2 , acting
towards the centre

47. b) A telecommunications satellite, of mass m, orbits Earth with constant
angular velocity  at a distance r from the centre of the Earth.
The gravitational force exerted by Earth on the satellite is Am where
r2
A is a constant. By considering all other forces on the satellite to be
negligible, show that;
A
r 3
 2

48. b) A telecommunications satellite, of mass m, orbits Earth with constant
angular velocity  at a distance r from the centre of the Earth.
The gravitational force exerted by Earth on the satellite is Am where
r2
A is a constant. By considering all other forces on the satellite to be
negligible, show that;
A
r 3
 2

49. b) A telecommunications satellite, of mass m, orbits Earth with constant
angular velocity  at a distance r from the centre of the Earth.
The gravitational force exerted by Earth on the satellite is Am where
r2
A is a constant. By considering all other forces on the satellite to be
negligible, show that;
A
r 3
 2
m  mr 2
x

50. b) A telecommunications satellite, of mass m, orbits Earth with constant
angular velocity  at a distance r from the centre of the Earth.
The gravitational force exerted by Earth on the satellite is Am where
r2
A is a constant. By considering all other forces on the satellite to be
negligible, show that;
A
r 3
 2
Am
m  mr 2
x
r2

51. b) A telecommunications satellite, of mass m, orbits Earth with constant
angular velocity  at a distance r from the centre of the Earth.
The gravitational force exerted by Earth on the satellite is Am where
r2
A is a constant. By considering all other forces on the satellite to be
negligible, show that;
A
r 3
 2
Am
mr 2 
Am r2
m  mr 2
x
r2

52. b) A telecommunications satellite, of mass m, orbits Earth with constant
angular velocity  at a distance r from the centre of the Earth.
The gravitational force exerted by Earth on the satellite is Am where
r2
A is a constant. By considering all other forces on the satellite to be
negligible, show that;
A
r 3
 2
Am
mr 2 
Am r2
m  mr 2
x
r2 Am
r3 
m 2
A
 2


53. b) A telecommunications satellite, of mass m, orbits Earth with constant
angular velocity  at a distance r from the centre of the Earth.
The gravitational force exerted by Earth on the satellite is Am where
r2
A is a constant. By considering all other forces on the satellite to be
negligible, show that;
A
r 3
 2
Am
mr 2 
Am r2
m  mr 2
x
r2 Am
r3 
m 2
A
 2

A
r3
2

54. (ii) A string is 50cm long and it will break if a ,mass exceeding 40kg is
hung from it.
A mass of 2kg is attached to one end of the string and it is revolved
in a circle.
Find the greatest angular velocity which may be imparted without
breaking the string.

55. (ii) A string is 50cm long and it will break if a ,mass exceeding 40kg is
hung from it.
A mass of 2kg is attached to one end of the string and it is revolved
in a circle.
Find the greatest angular velocity which may be imparted without
breaking the string.

56. (ii) A string is 50cm long and it will break if a ,mass exceeding 40kg is
hung from it.
A mass of 2kg is attached to one end of the string and it is revolved
in a circle.
Find the greatest angular velocity which may be imparted without
breaking the string.
m
x

57. (ii) A string is 50cm long and it will break if a ,mass exceeding 40kg is
hung from it.
A mass of 2kg is attached to one end of the string and it is revolved
in a circle.
Find the greatest angular velocity which may be imparted without
breaking the string.
m
x mg

58. (ii) A string is 50cm long and it will break if a ,mass exceeding 40kg is
hung from it.
A mass of 2kg is attached to one end of the string and it is revolved
in a circle.
Find the greatest angular velocity which may be imparted without
breaking the string.
T
m
x mg

59. (ii) A string is 50cm long and it will break if a ,mass exceeding 40kg is
hung from it.
A mass of 2kg is attached to one end of the string and it is revolved
in a circle.
Find the greatest angular velocity which may be imparted without
breaking the string.
m  mg  T
x
T
m
x mg

60. (ii) A string is 50cm long and it will break if a ,mass exceeding 40kg is
hung from it.
A mass of 2kg is attached to one end of the string and it is revolved
in a circle.
Find the greatest angular velocity which may be imparted without
breaking the string.
m  mg  T
x
T 0  mg  T
m
x mg

61. (ii) A string is 50cm long and it will break if a ,mass exceeding 40kg is
hung from it.
A mass of 2kg is attached to one end of the string and it is revolved
in a circle.
Find the greatest angular velocity which may be imparted without
breaking the string.
m  mg  T
x
T 0  mg  T
T  40 9.8
 392 N
m
x mg

62. (ii) A string is 50cm long and it will break if a ,mass exceeding 40kg is
hung from it.
A mass of 2kg is attached to one end of the string and it is revolved
in a circle.
Find the greatest angular velocity which may be imparted without
breaking the string.
m  mg  T
x
T 0  mg  T
T  40 9.8
 392 N
m
x mg

63. (ii) A string is 50cm long and it will break if a ,mass exceeding 40kg is
hung from it.
A mass of 2kg is attached to one end of the string and it is revolved
in a circle.
Find the greatest angular velocity which may be imparted without
breaking the string. m
x
m  mg  T
x
T 0  mg  T
T  40 9.8
 392 N
m
x mg

64. (ii) A string is 50cm long and it will break if a ,mass exceeding 40kg is
hung from it.
A mass of 2kg is attached to one end of the string and it is revolved
in a circle.
Find the greatest angular velocity which may be imparted without
breaking the string. m
x
T
m  mg  T
x
T 0  mg  T
T  40 9.8
 392 N
m
x mg

65. (ii) A string is 50cm long and it will break if a ,mass exceeding 40kg is
hung from it.
A mass of 2kg is attached to one end of the string and it is revolved
in a circle.
Find the greatest angular velocity which may be imparted without
breaking the string. m
x
T
m  mg  T
x T  mr 2
T 0  mg  T
T  40 9.8
 392 N
m
x mg

66. (ii) A string is 50cm long and it will break if a ,mass exceeding 40kg is
hung from it.
A mass of 2kg is attached to one end of the string and it is revolved
in a circle.
Find the greatest angular velocity which may be imparted without
breaking the string. m
x
T
m  mg  T
x T  mr 2
0  mg  T
T 392  2 0.5 2
T  40 9.8
 392 N
m
x mg

67. (ii) A string is 50cm long and it will break if a ,mass exceeding 40kg is
hung from it.
A mass of 2kg is attached to one end of the string and it is revolved
in a circle.
Find the greatest angular velocity which may be imparted without
breaking the string. m
x
T
m  mg  T
x T  mr 2
0  mg  T
T 392  2 0.5 2
T  40 9.8
 2  392
 392 N
mg
  392
m
x
  2 98rad/s

68. (ii) A string is 50cm long and it will break if a ,mass exceeding 40kg is
hung from it.
A mass of 2kg is attached to one end of the string and it is revolved
in a circle.
Find the greatest angular velocity which may be imparted without
breaking the string. m
x
T
m  mg  T
x T  mr 2
0  mg  T
T 392  2 0.5 2
T  40 9.8
 2  392
 392 N
mg
  392
m
x
  2 98rad/s
Exercise 9B; all