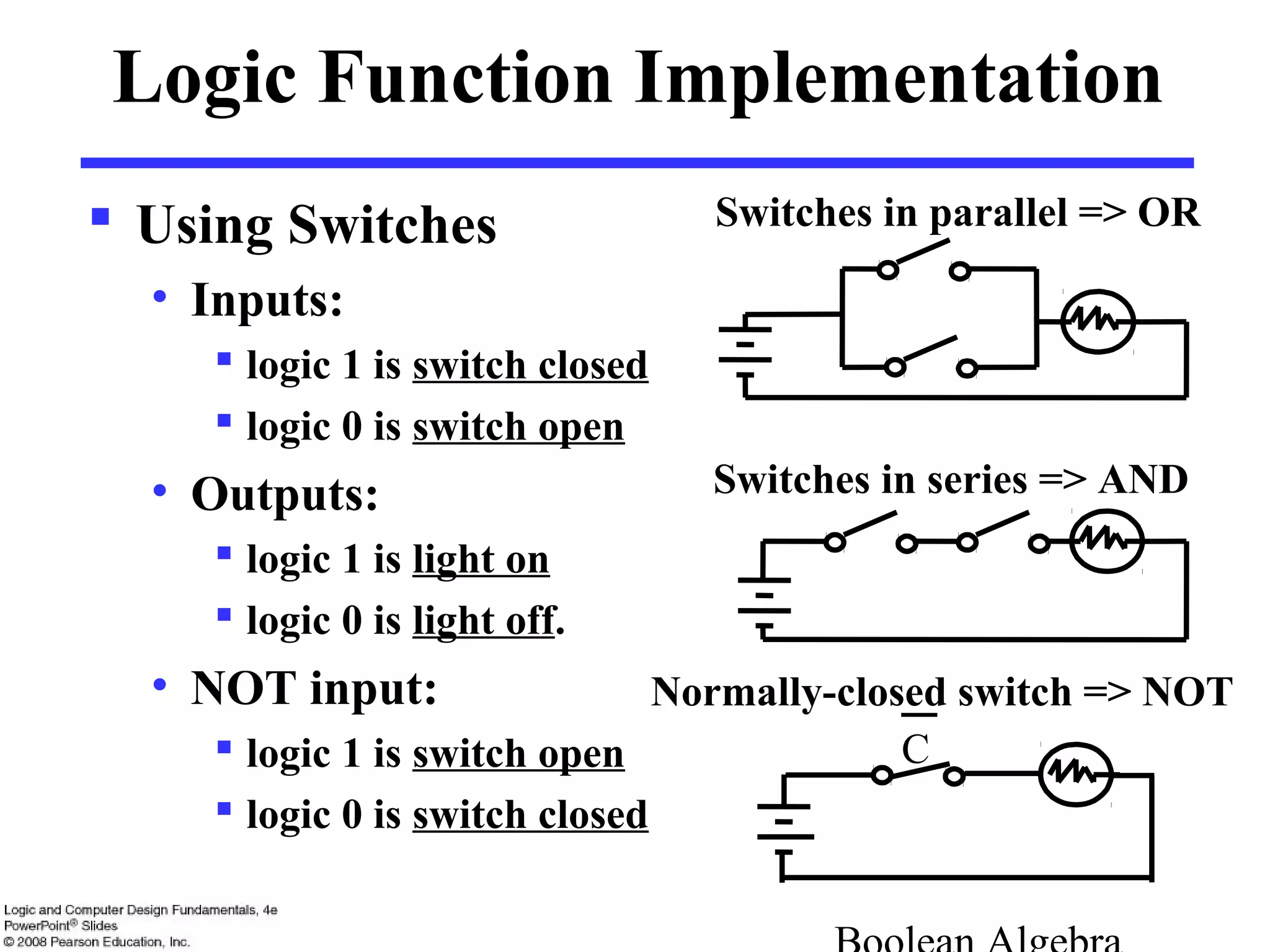
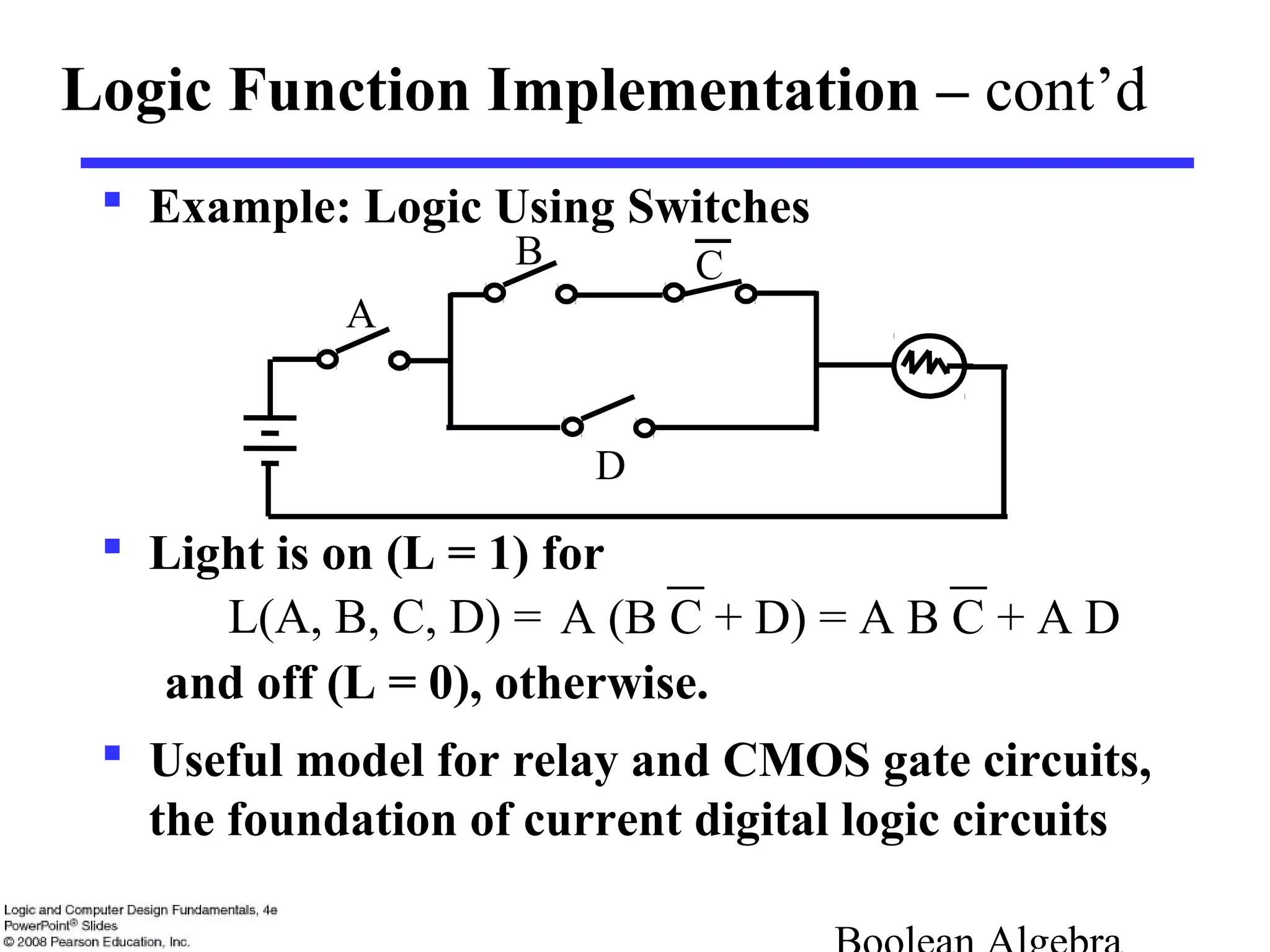
1. Boolean algebra is a mathematical system used to specify and transform logic functions. It uses binary variables that take on values of 1 or 0 and logical operators like AND, OR, and NOT.
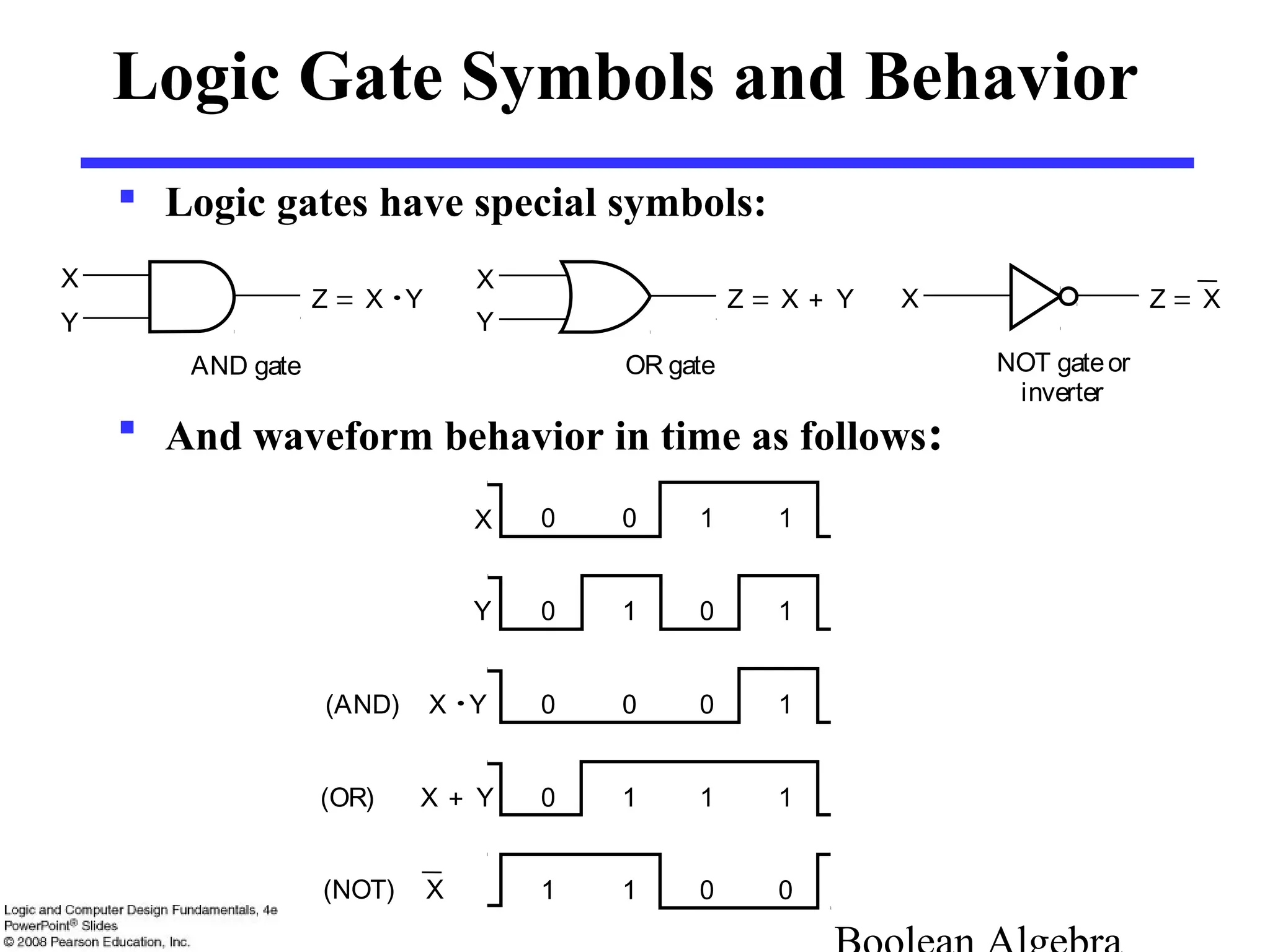
2. Logic gates implement logic functions physically using electronic components. Common gates are AND, OR, and NOT. Gates have a small but nonzero delay between input change and output change.
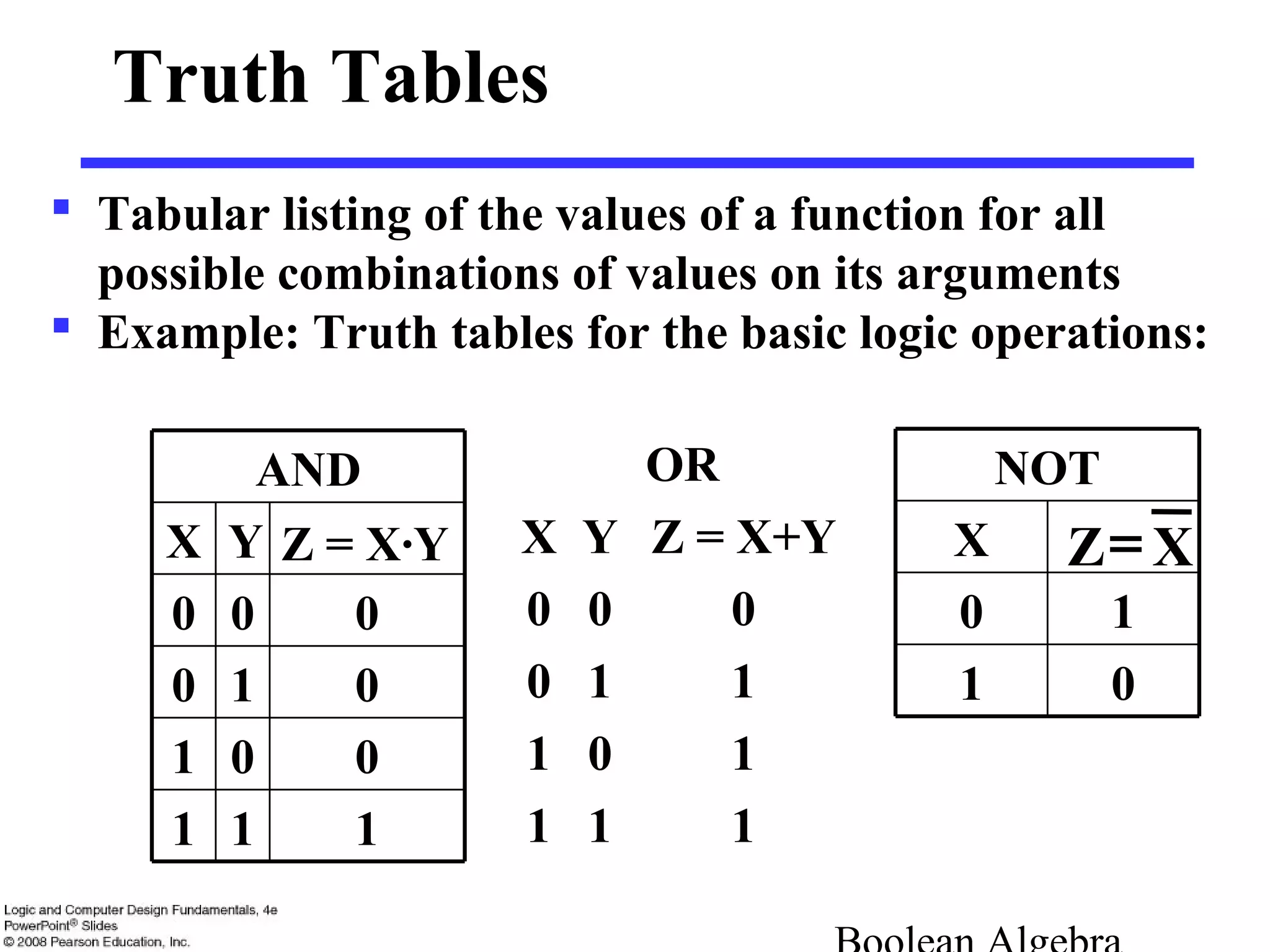
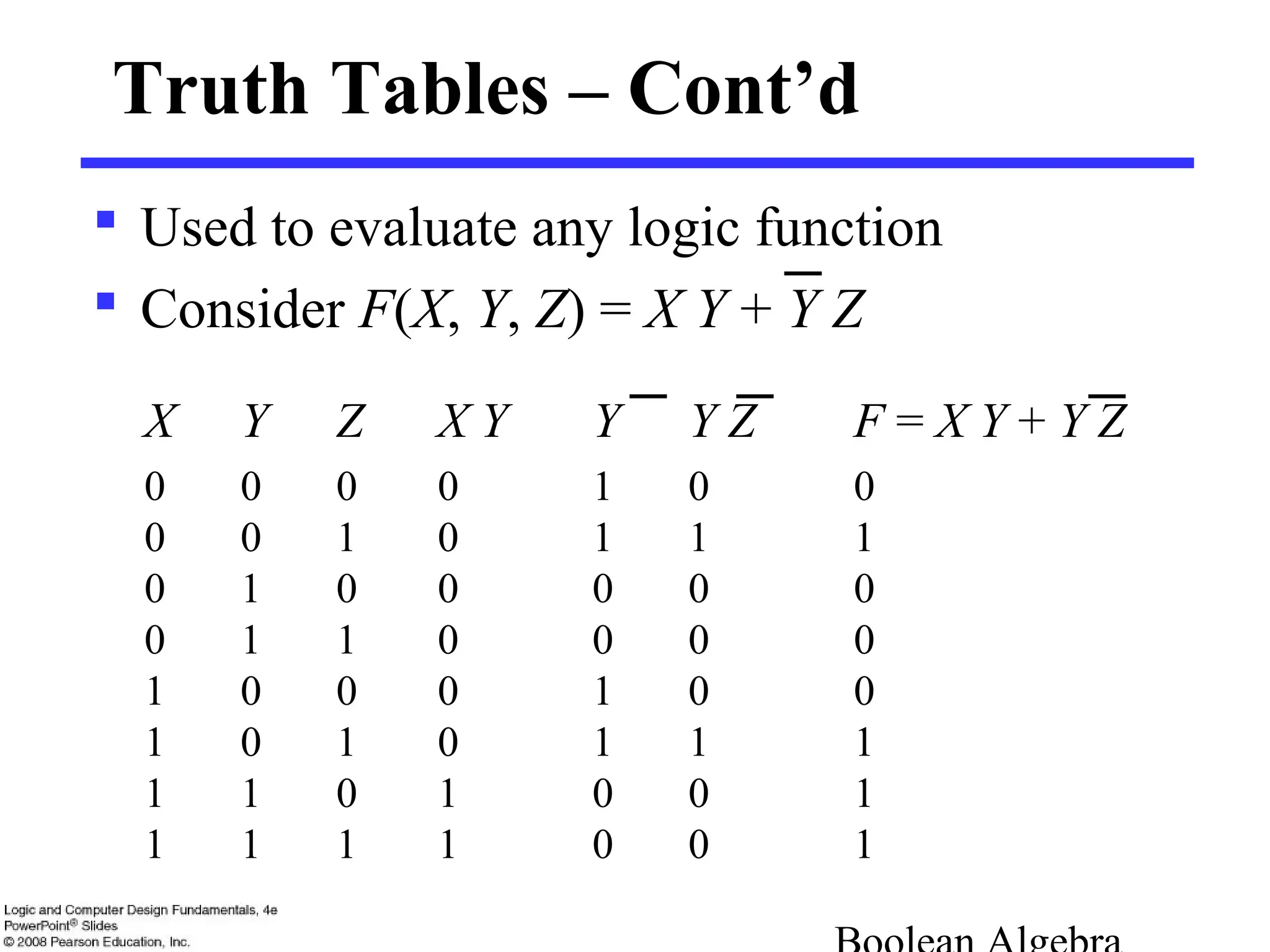
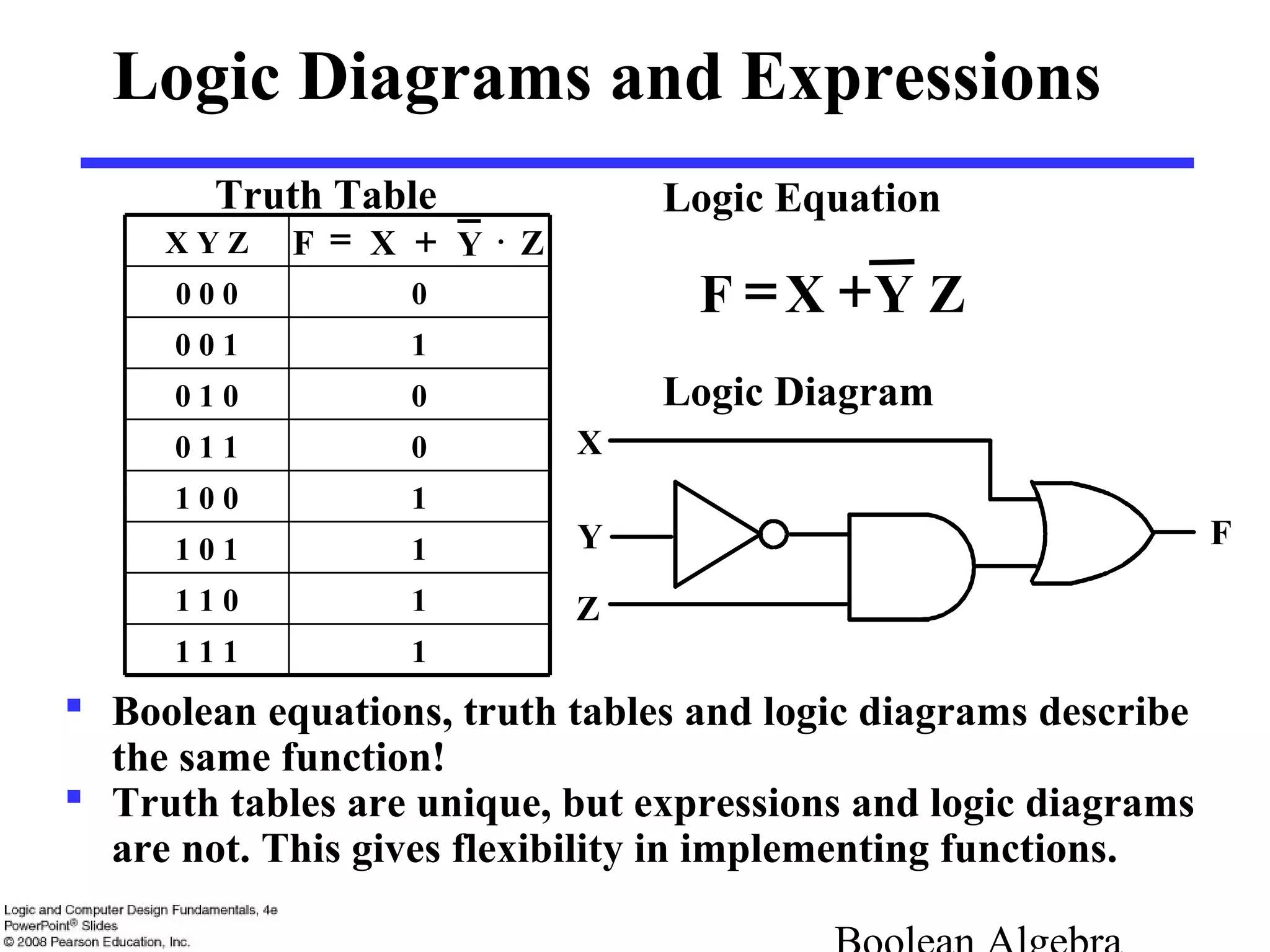
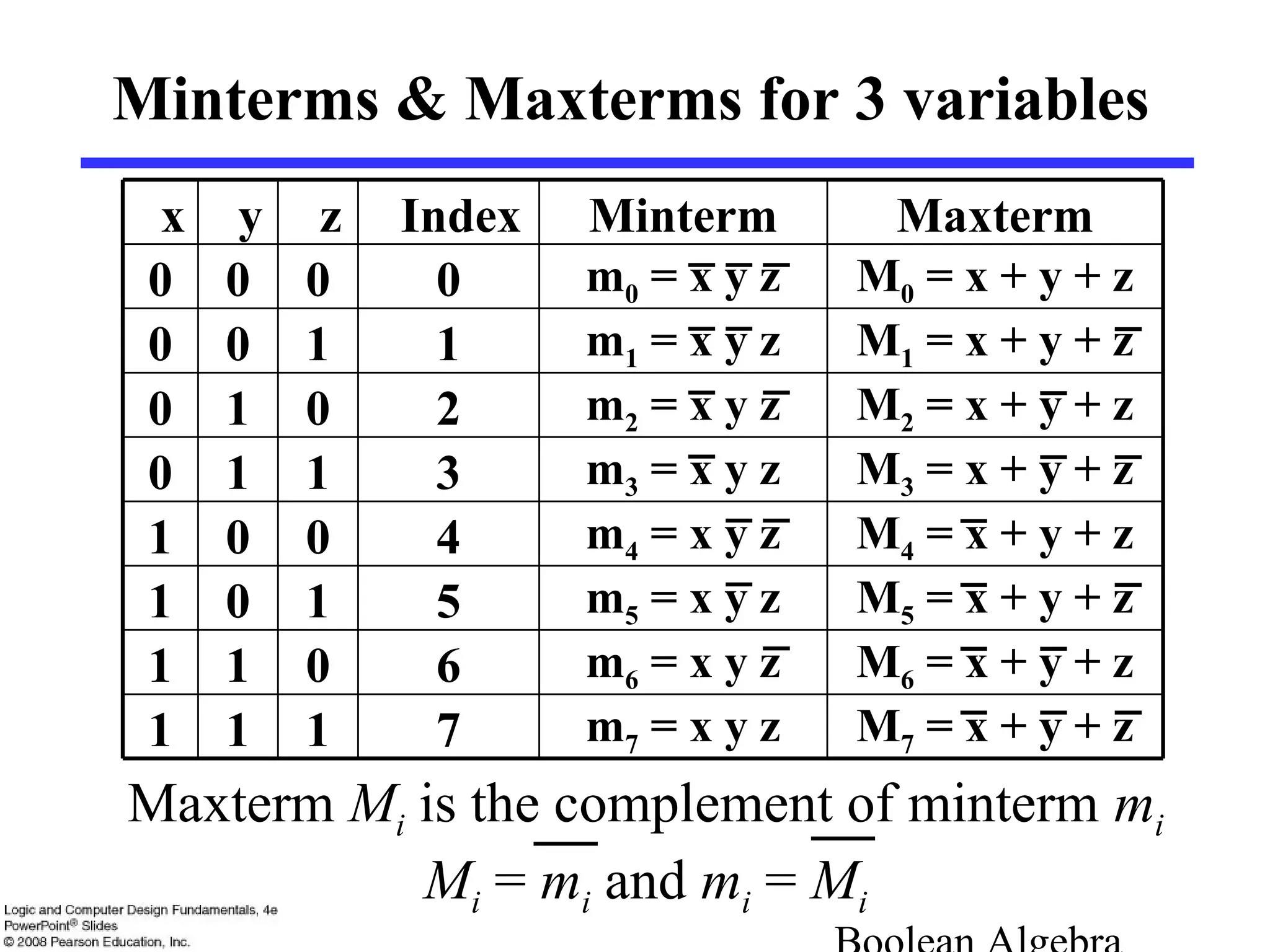
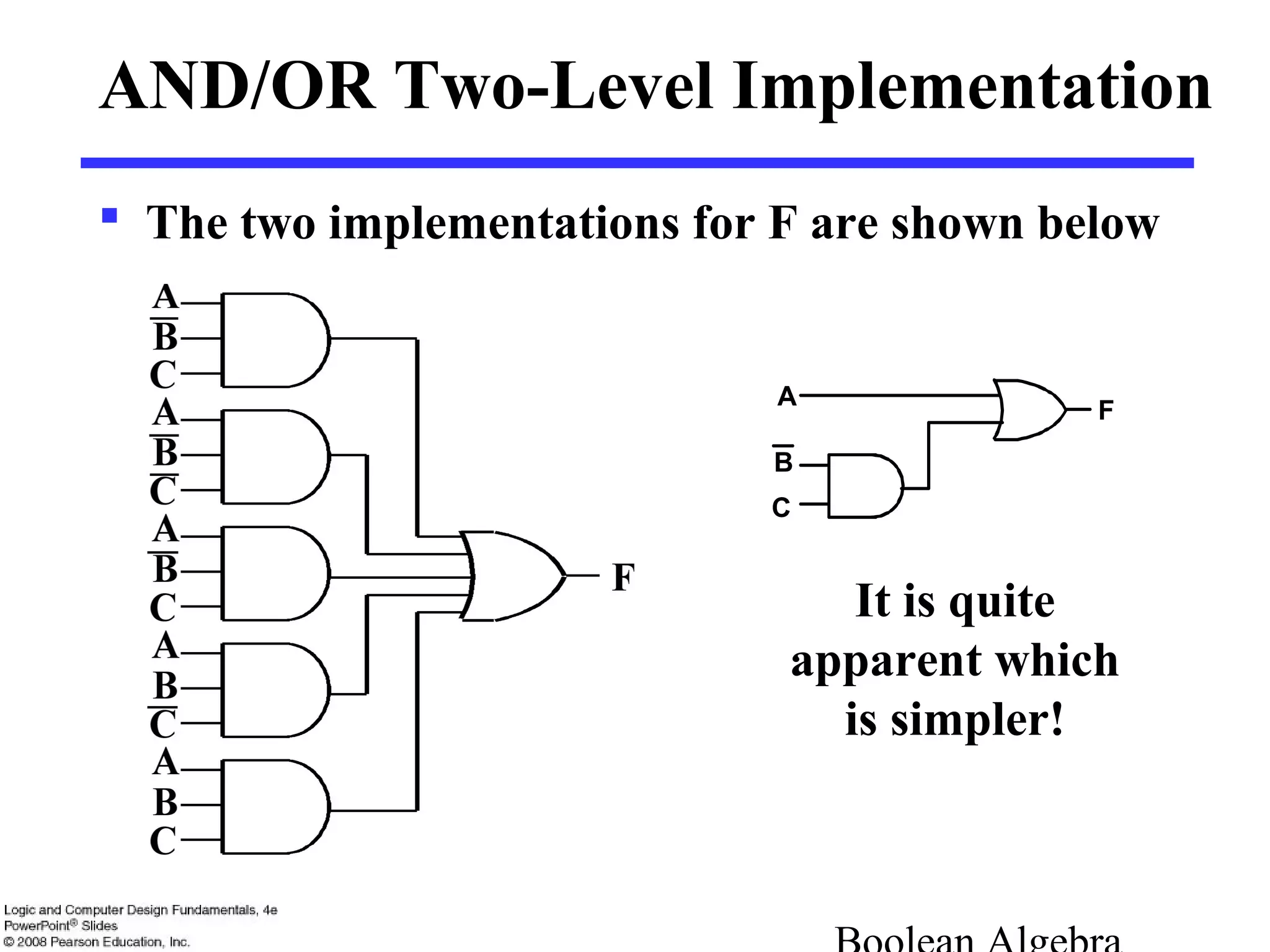
3. Boolean expressions can be represented using truth tables, logic diagrams, or algebraic expressions. Standard forms include sum-of-minterms and product-of-maxterms forms.