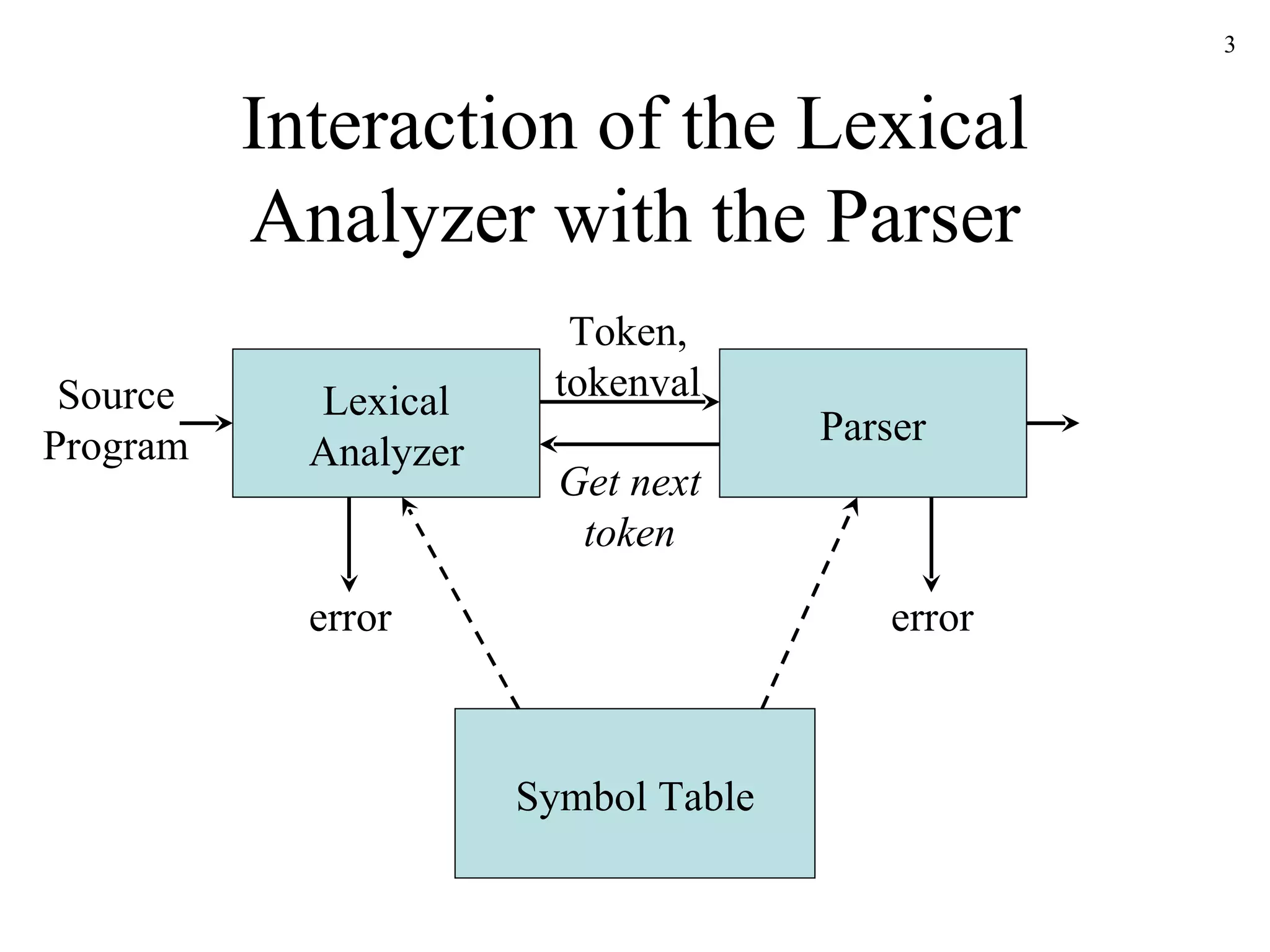
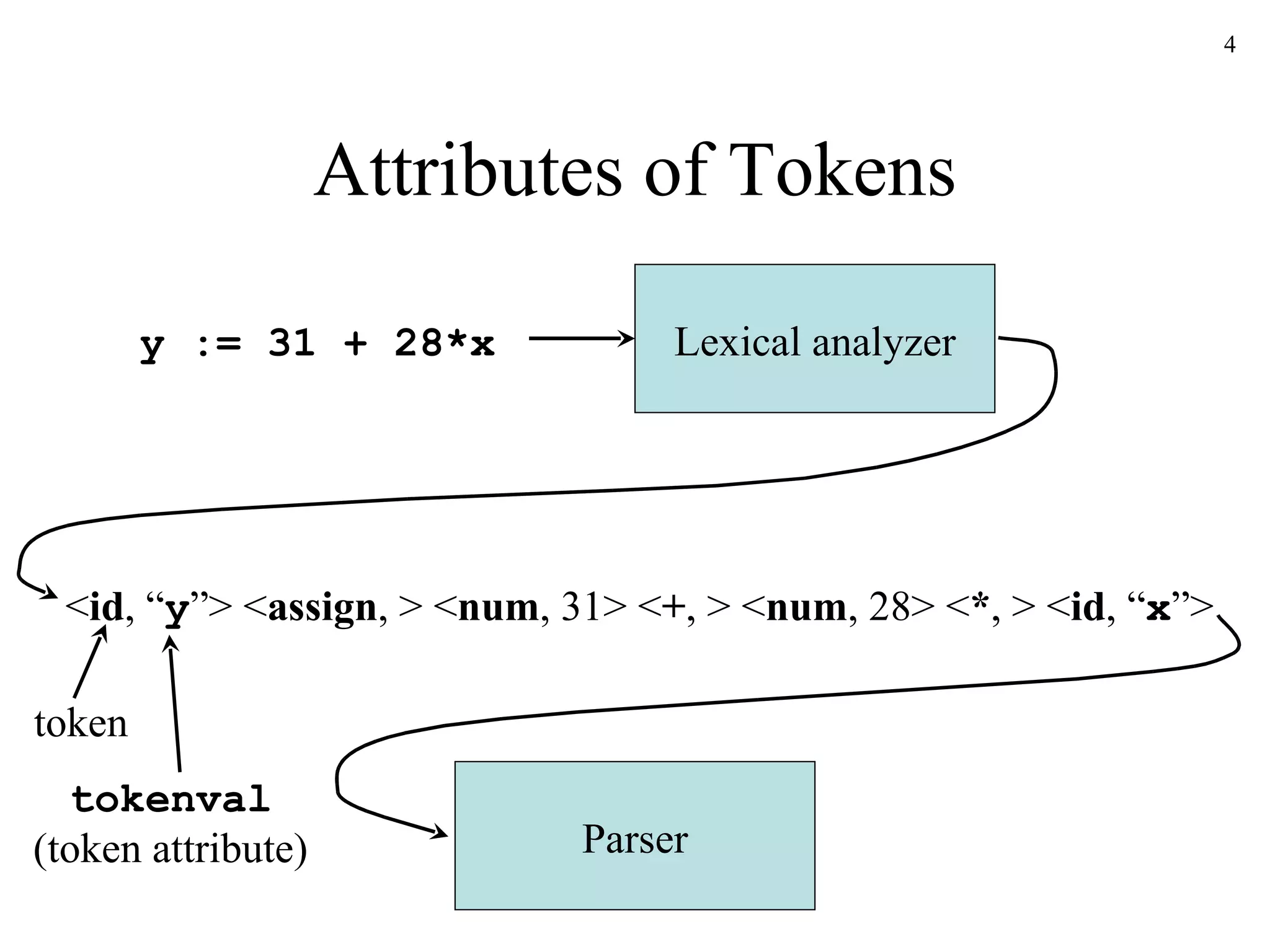
The document discusses lexical analysis and lexical analyzer generators. It provides background on why lexical analysis is a separate phase in compiler design and how it simplifies parsing. It also describes how a lexical analyzer interacts with a parser and some key attributes of tokens like lexemes and patterns. Finally, it explains how regular expressions are used to specify patterns for tokens and how tools like Lex and Flex can be used to generate lexical analyzers from regular expression definitions.

1. Lexical Analysis and Lexical Analyzer Generators Chapter 3 COP5621 Compiler Construction Copyright Robert van Engelen, Florida State University, 2007-2009

2. The Reason Why Lexical Analysis is a Separate Phase Simplifies the design of the compiler LL(1) or LR(1) parsing with 1 token lookahead would not be possible (multiple characters/tokens to match) Provides efficient implementation Systematic techniques to implement lexical analyzers by hand or automatically from specifications Stream buffering methods to scan input Improves portability Non-standard symbols and alternate character encodings can be normalized (e.g. trigraphs)

3. Interaction of the Lexical Analyzer with the Parser Lexical Analyzer Parser Source Program Token, tokenval Symbol Table Get next token error error

4. Attributes of Tokens Lexical analyzer < id , “ y ”> < assign , > < num , 31> < + , > < num , 28> < * , > < id , “ x ”> y := 31 + 28*x Parser token tokenval (token attribute)

5. Tokens, Patterns, and Lexemes A token is a classification of lexical units For example: id and num Lexemes are the specific character strings that make up a token For example: abc and 123 Patterns are rules describing the set of lexemes belonging to a token For example: “ letter followed by letters and digits” and “ non-empty sequence of digits ”

6. Specification of Patterns for Tokens: Definitions An alphabet  is a finite set of symbols (characters) A string s is a finite sequence of symbols from   s  denotes the length of string s  denotes the empty string, thus  = 0 A language is a specific set of strings over some fixed alphabet 

7. Specification of Patterns for Tokens: String Operations The concatenation of two strings x and y is denoted by xy The exponentation of a string s is defined by s 0 =  s i = s i- 1 s for i > 0 note that s  =  s = s

8. Specification of Patterns for Tokens: Language Operations Union L  M = { s  s  L or s  M } Concatenation LM = { xy  x  L and y  M } Exponentiation L 0 = {  }; L i = L i -1 L Kleene closure L * =  i =0,…,  L i Positive closure L + =  i =1,…,  L i

9. Specification of Patterns for Tokens: Regular Expressions Basis symbols:  is a regular expression denoting language {  } a   is a regular expression denoting { a } If r and s are regular expressions denoting languages L ( r ) and M ( s ) respectively, then r  s is a regular expression denoting L ( r )  M ( s ) rs is a regular expression denoting L ( r ) M ( s ) r * is a regular expression denoting L ( r ) * ( r ) is a regular expression denoting L ( r ) A language defined by a regular expression is called a regular set

10. Specification of Patterns for Tokens: Regular Definitions Regular definitions introduce a naming convention: d 1  r 1 d 2  r 2 … d n  r n where each r i is a regular expression over   { d 1 , d 2 , …, d i -1 } Any d j in r i can be textually substituted in r i to obtain an equivalent set of definitions

11. Specification of Patterns for Tokens: Regular Definitions Example: letter  A  B  …  Z  a  b  …  z digit  0  1  …  9 id  letter ( letter  digit ) * Regular definitions are not recursive: digits  digit digits  digit wrong!

12. Specification of Patterns for Tokens: Notational Shorthand The following shorthands are often used: r + = rr * r ? = r  [ a - z ] = a  b  c  …  z Examples: digit  [ 0 - 9 ] num  digit + ( . digit + )? ( E ( +  - )? digit + )?

13. Regular Definitions and Grammars stmt  if expr then stmt  if expr then stmt else stmt   expr  term relop term  term term  id  num if  if then  then else  else relop  <  <=  <>  >  >=  = id  letter ( letter | digit ) * num  digit + ( . digit + )? ( E ( +  - )? digit + )? Grammar Regular definitions

14. Coding Regular Definitions in Transition Diagrams 0 2 1 6 3 4 5 7 8 return ( relop , LE ) return ( relop , NE ) return ( relop , LT ) return ( relop , EQ ) return ( relop , GE ) return ( relop , GT ) start < = > = > = other other * * 9 start letter 10 11 * other letter or digit return ( gettoken (), install_id ()) relop  <  <=  <>  >  >=  = id  letter ( letter  digit ) *

15. Coding Regular Definitions in Transition Diagrams: Code token nexttoken() { while (1) { switch (state) { case 0: c = nextchar(); if (c==blank || c==tab || c==newline) { state = 0; lexeme_beginning++; } else if (c==‘<’) state = 1; else if (c==‘=’) state = 5; else if (c==‘>’) state = 6; else state = fail(); break ; case 1: … case 9: c = nextchar(); if (isletter(c)) state = 10; else state = fail(); break ; case 10: c = nextchar(); if (isletter(c)) state = 10; else if (isdigit(c)) state = 10; else state = 11; break ; … int fail() { forward = token_beginning; swith (start) { case 0: start = 9; break ; case 9: start = 12; break ; case 12: start = 20; break ; case 20: start = 25; break ; case 25: recover(); break ; default : /* error */ } return start; } Decides the next start state to check

16. The Lex and Flex Scanner Generators Lex and its newer cousin flex are scanner generators Systematically translate regular definitions into C source code for efficient scanning Generated code is easy to integrate in C applications

17. Creating a Lexical Analyzer with Lex and Flex lex or flex compiler lex source program lex.l lex.yy.c input stream C compiler a.out sequence of tokens lex.yy.c a.out

18. Lex Specification A lex specification consists of three parts: regular definitions, C declarations in %{ %} %% translation rules %% user-defined auxiliary procedures The translation rules are of the form: p 1 { action 1 } p 2 { action 2 } … p n { action n }

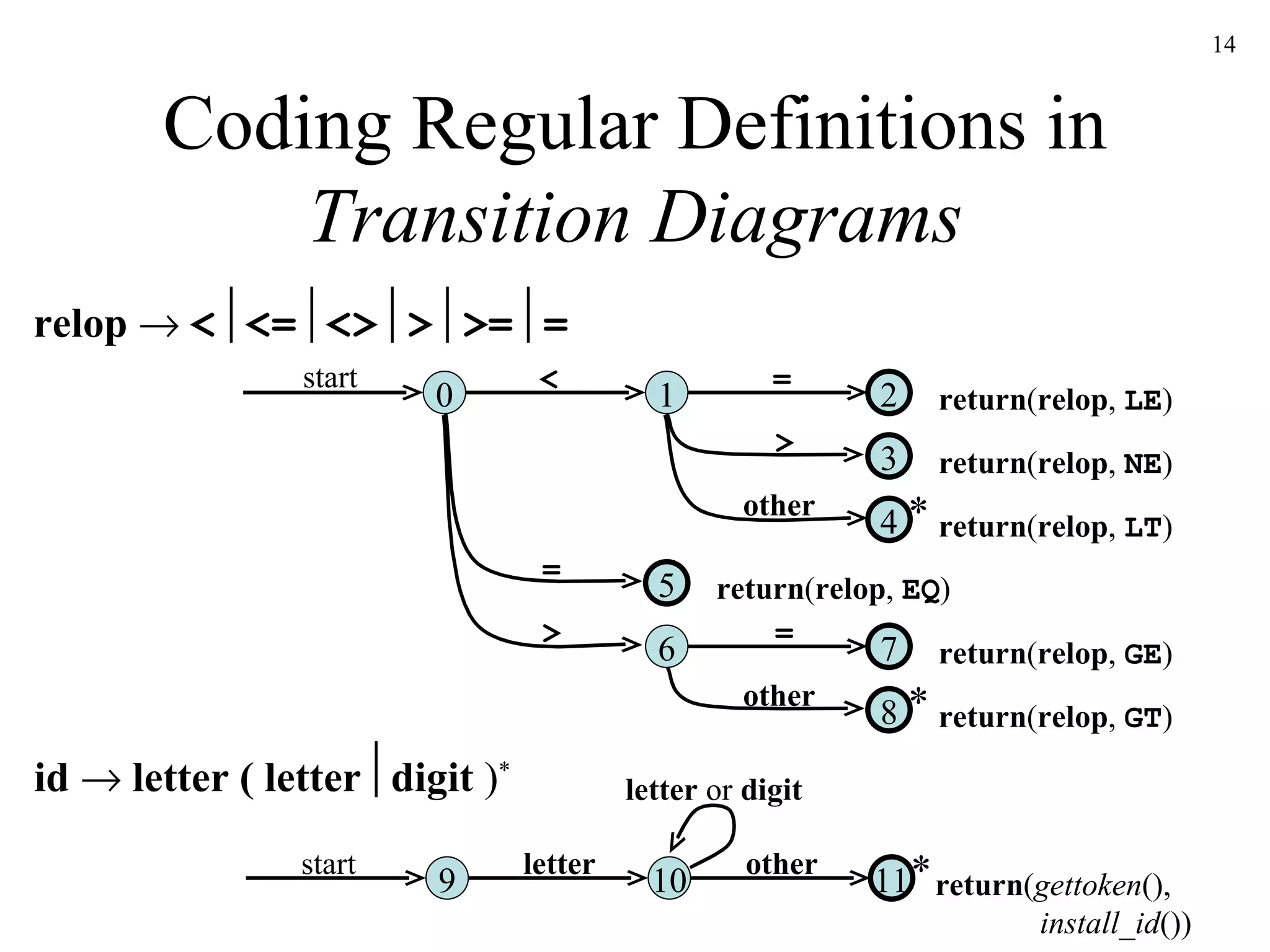
19. Regular Expressions in Lex x match the character x \. match the character . “ string ” match contents of string of characters . match any character except newline ^ match beginning of a line $ match the end of a line [xyz] match one character x , y , or z (use \ to escape - ) [^xyz] match any character except x , y , and z [a-z] match one of a to z r * closure (match zero or more occurrences) r + positive closure (match one or more occurrences) r ? optional (match zero or one occurrence) r 1 r 2 match r 1 then r 2 (concatenation) r 1 | r 2 match r 1 or r 2 (union) ( r ) grouping r 1 \ r 2 match r 1 when followed by r 2 { d } match the regular expression defined by d

20. Example Lex Specification 1 %{ #include <stdio.h> %} %% [0-9]+ { printf(“%s\n”, yytext); } .|\n { } %% main() { yylex(); } Contains the matching lexeme Invokes the lexical analyzer lex spec.l gcc lex.yy.c -ll ./a.out < spec.l Translation rules

21. Example Lex Specification 2 %{ #include <stdio.h> int ch = 0, wd = 0, nl = 0; %} delim [ \t]+ %% \n { ch++; wd++; nl++; } ^{delim} { ch+=yyleng; } {delim} { ch+=yyleng; wd++; } . { ch++; } %% main() { yylex(); printf(&quot;%8d%8d%8d\n&quot;, nl, wd, ch); } Regular definition Translation rules

22. Example Lex Specification 3 %{ #include <stdio.h> %} digit [0-9] letter [A-Za-z] id {letter}({letter}|{digit})* %% {digit}+ { printf(“number: %s\n”, yytext); } {id} { printf(“ident: %s\n”, yytext); } . { printf(“other: %s\n”, yytext); } %% main() { yylex(); } Regular definitions Translation rules

23. Example Lex Specification 4 %{ /* definitions of manifest constants */ #define LT (256) … %} delim [ \t\n] ws {delim}+ letter [A-Za-z] digit [0-9] id {letter}({letter}|{digit})* number {digit}+(\.{digit}+)?(E[+\-]?{digit}+)? %% {ws} { } if {return IF;} then {return THEN;} else {return ELSE;} {id} {yylval = install_id(); return ID;} {number} {yylval = install_num(); return NUMBER;} “<“ {yylval = LT; return RELOP;} “<=“ {yylval = LE; return RELOP;} “ =“ {yylval = EQ; return RELOP;} “ <>“ {yylval = NE; return RELOP;} “>“ {yylval = GT; return RELOP;} “ >=“ {yylval = GE; return RELOP;} %% int install_id() … Return token to parser Token attribute Install yytext as identifier in symbol table

24. Design of a Lexical Analyzer Generator Translate regular expressions to NFA Translate NFA to an efficient DFA regular expressions NFA DFA Simulate NFA to recognize tokens Simulate DFA to recognize tokens Optional

25. Nondeterministic Finite Automata An NFA is a 5-tuple ( S ,  ,  , s 0 , F ) where S is a finite set of states  is a finite set of symbols, the alphabet  is a mapping from S   to a set of states s 0  S is the start state F  S is the set of accepting ( or final) states

26. Transition Graph An NFA can be diagrammatically represented by a labeled directed graph called a transition graph 0 start a 1 3 2 b b a b S = {0,1,2,3}  = { a , b } s 0 = 0 F = {3}

27. Transition Table The mapping  of an NFA can be represented in a transition table  (0, a ) = {0,1}  (0, b ) = {0}  (1, b ) = {2}  (2, b ) = {3} State Input a Input b 0 {0, 1} {0} 1 {2} 2 {3}

28. The Language Defined by an NFA An NFA accepts an input string x if and only if there is some path with edges labeled with symbols from x in sequence from the start state to some accepting state in the transition graph A state transition from one state to another on the path is called a move The language defined by an NFA is the set of input strings it accepts, such as ( a  b )* abb for the example NFA

29. Design of a Lexical Analyzer Generator: RE to NFA to DFA s 0 N ( p 1 ) N ( p 2 ) start   N ( p n )  … p 1 { action 1 } p 2 { action 2 } … p n { action n } action 1 action 2 action n Lex specification with regular expressions NFA DFA Subset construction

30. From Regular Expression to NFA (Thompson’s Construction) N ( r 2 ) N ( r 1 ) f i  f a i f i N ( r 1 ) N ( r 2 ) start start start     f i start N ( r ) f i start    a r 1  r 2 r 1 r 2 r *  

31. Combining the NFAs of a Set of Regular Expressions 2 a 1 start 6 a 3 start 4 5 b b 8 b 7 start a b a { action 1 } abb { action 2 } a * b + { action 3 } 2 a 1 6 a 3 4 5 b b 8 b 7 a b 0 start   

32. Simulating the Combined NFA Example 1 2 a 1 6 a 3 4 5 b b 8 b 7 a b 0 start    Must find the longest match : Continue until no further moves are possible When last state is accepting: execute action action 1 action 2 action 3 a b a a none action 3 0 1 3 7 2 4 7 7 8

33. Simulating the Combined NFA Example 2 2 a 1 6 a 3 4 5 b b 8 b 7 a b 0 start    When two or more accepting states are reached, the first action given in the Lex specification is executed action 1 action 2 action 3 a b b a none action 2 action 3 0 1 3 7 2 4 7 5 8 6 8

34. Deterministic Finite Automata A deterministic finite automaton is a special case of an NFA No state has an  -transition For each state s and input symbol a there is at most one edge labeled a leaving s Each entry in the transition table is a single state At most one path exists to accept a string Simulation algorithm is simple

35. Example DFA 0 start a 1 3 2 b b b b a a a A DFA that accepts ( a  b )* abb

36. Conversion of an NFA into a DFA The subset construction algorithm converts an NFA into a DFA using:  -closure ( s ) = { s }  { t  s   …   t }  -closure ( T ) =  s  T  -closure ( s ) move ( T , a ) = { t  s  a t and s  T } The algorithm produces: Dstates is the set of states of the new DFA consisting of sets of states of the NFA Dtran is the transition table of the new DFA

37.  -closure and move Examples 2 a 1 6 a 3 4 5 b b 8 b 7 a b 0 start     -closure ({0}) = {0,1,3,7} move ({0,1,3,7}, a ) = {2,4,7}  -closure ({2,4,7}) = {2,4,7} move ({2,4,7}, a ) = {7}  -closure ({7}) = {7} move ({7}, b ) = {8}  -closure ({8}) = {8} move ({8}, a ) =  a b a a none Also used to simulate NFAs 0 1 3 7 2 4 7 7 8

38. Simulating an NFA using  -closure and move S :=  -closure ({ s 0 }) S prev :=  a := nextchar () while S   do S prev := S S :=  -closure ( move ( S,a )) a := nextchar () end do if S prev  F   then execute action in S prev return “yes” else return “no”

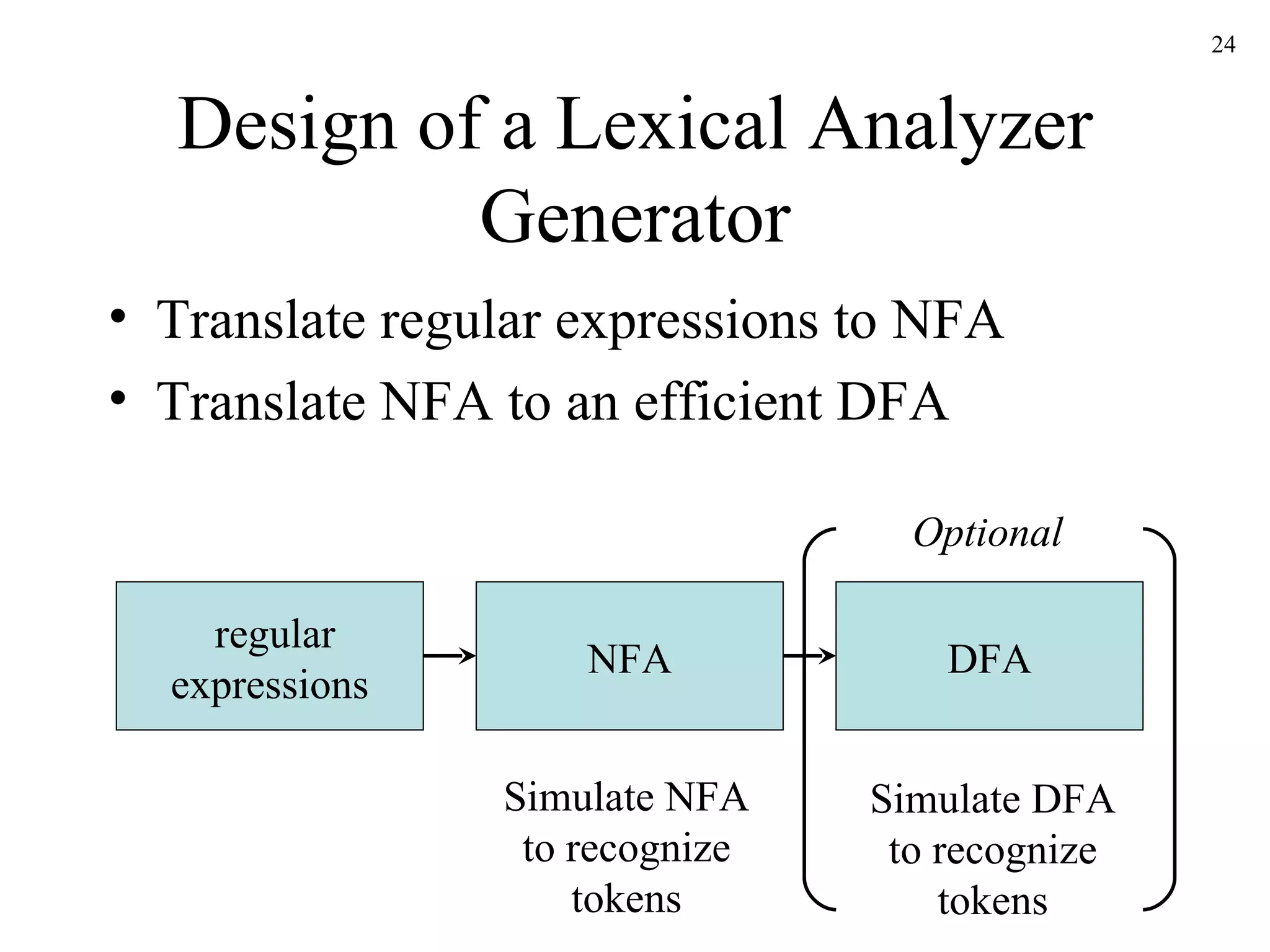
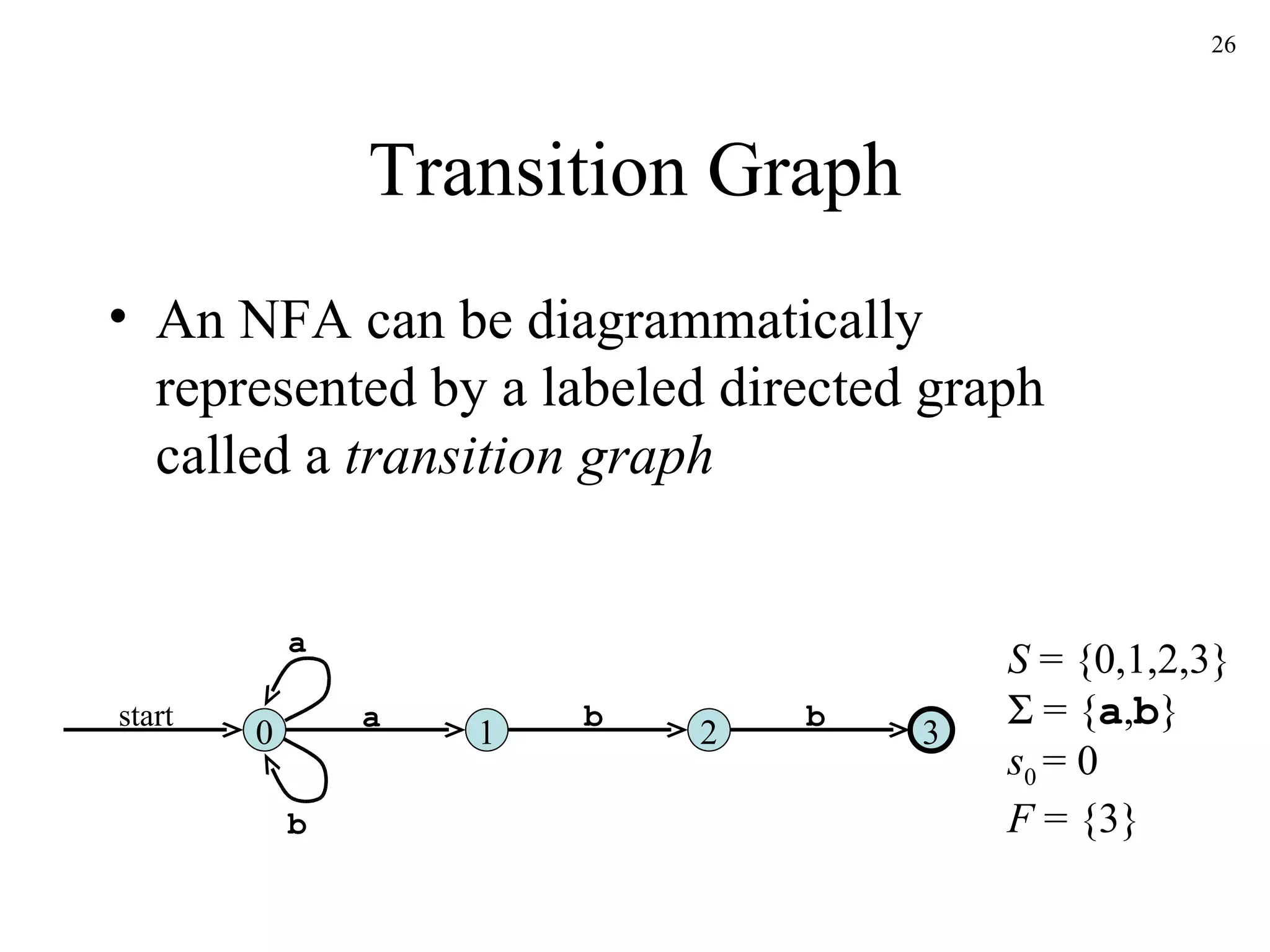
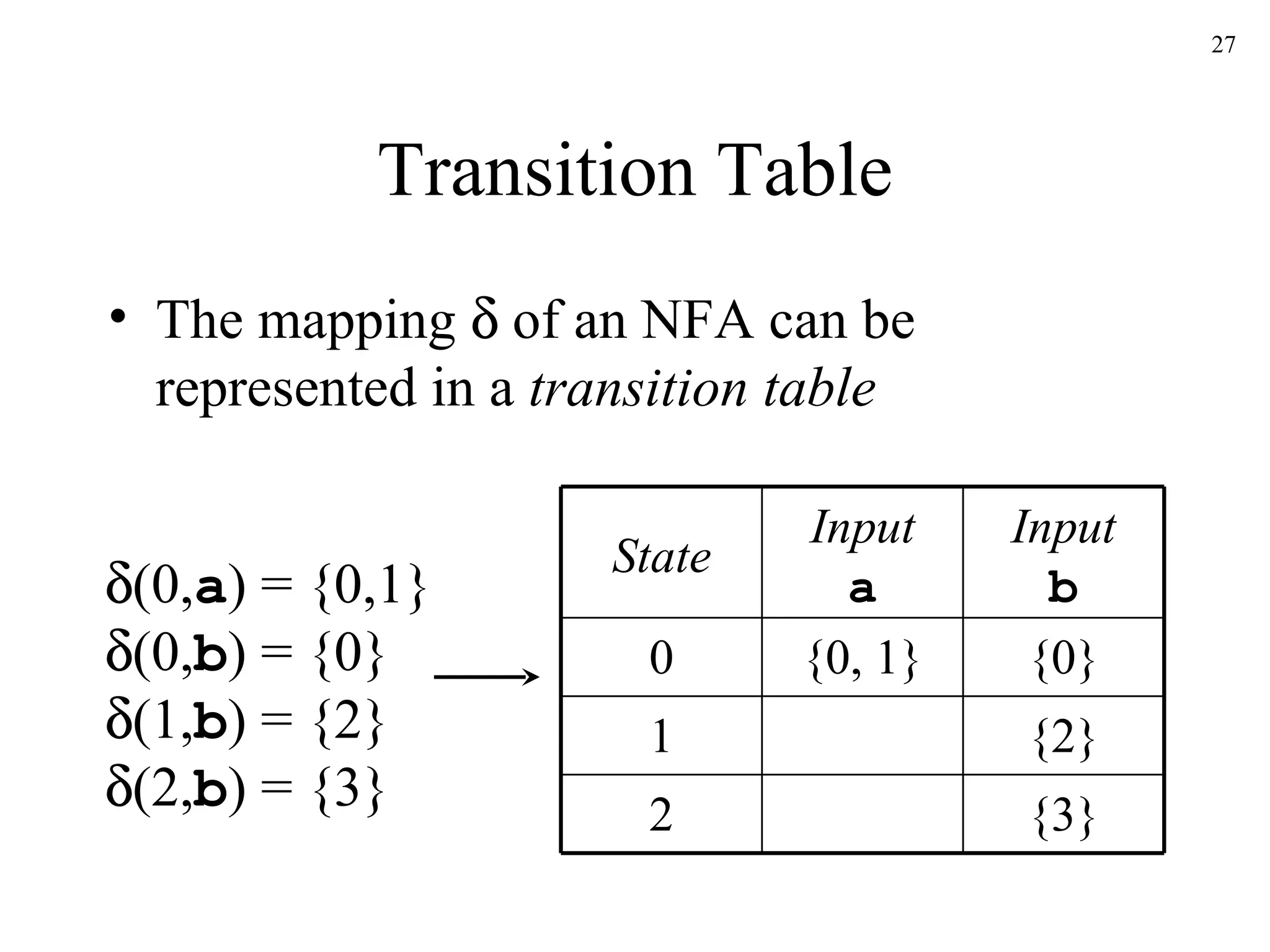
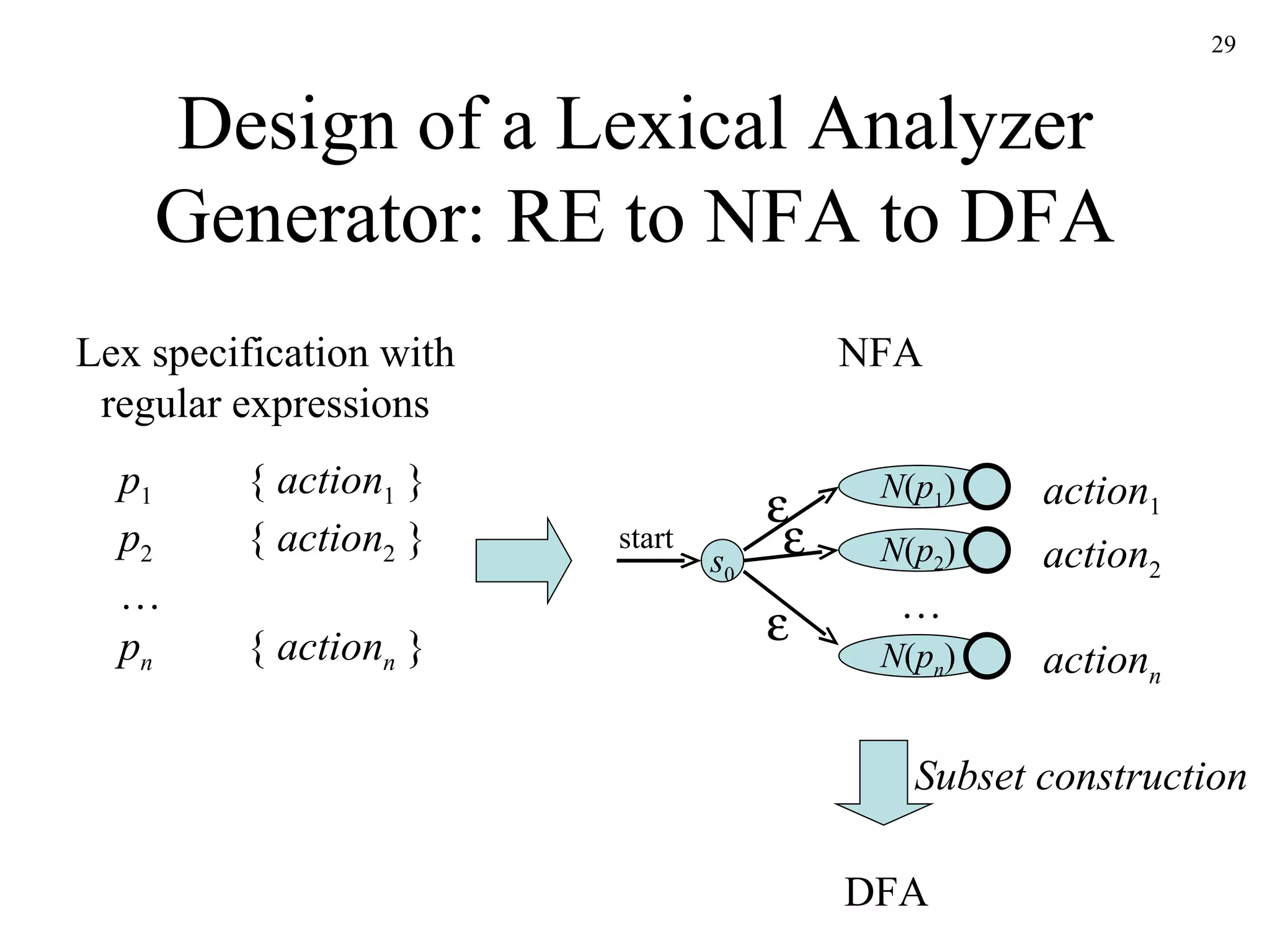
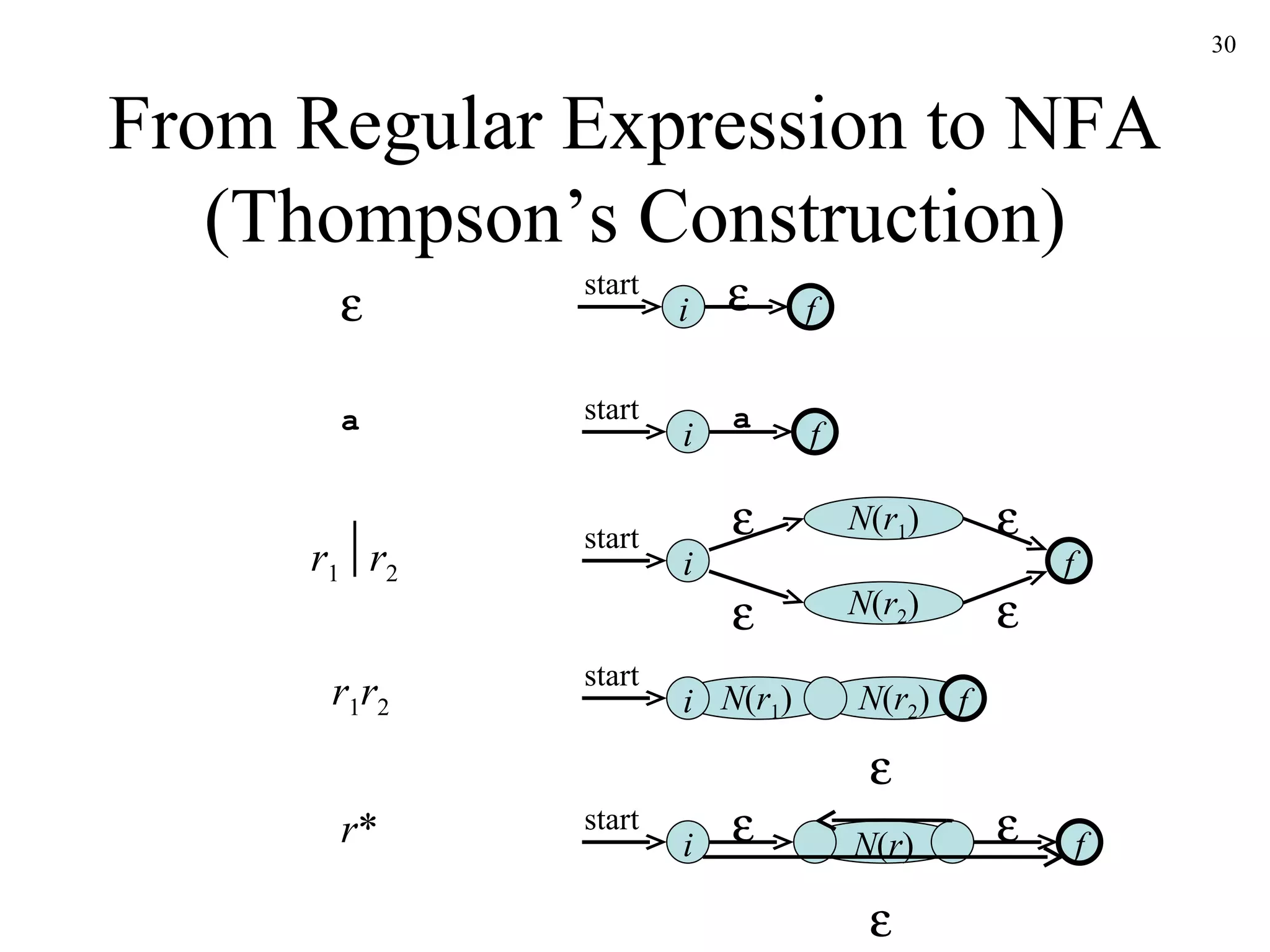
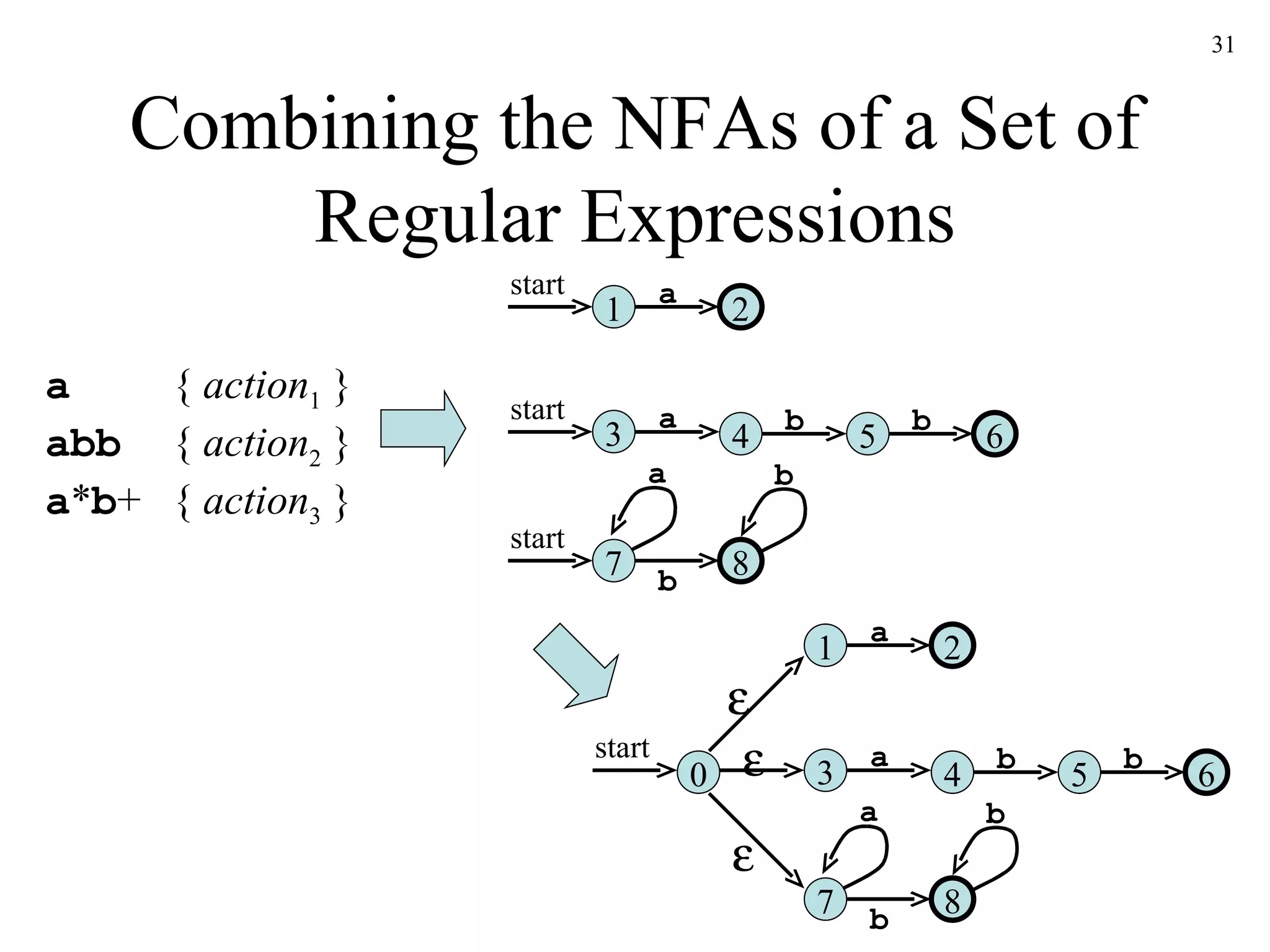
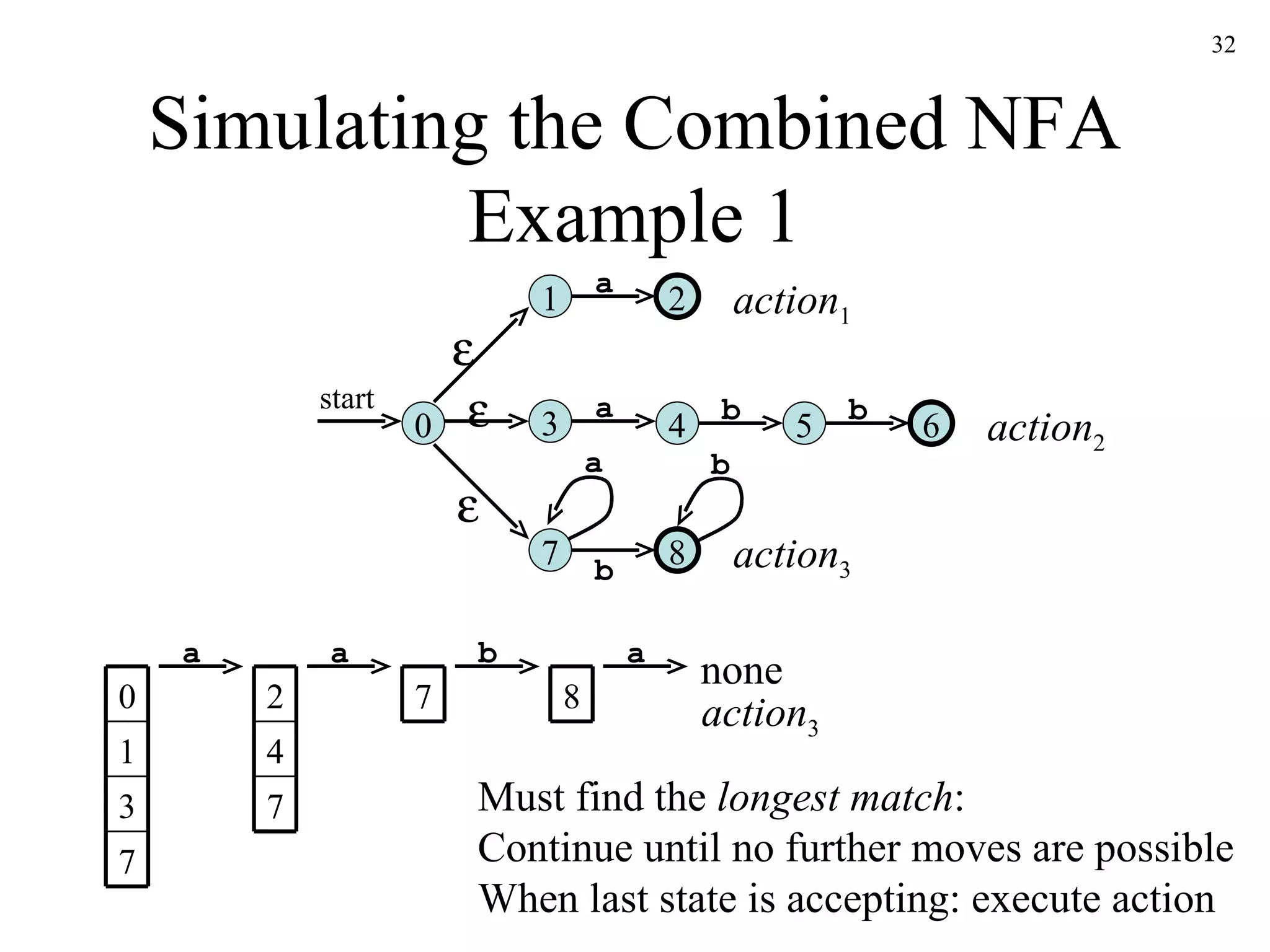
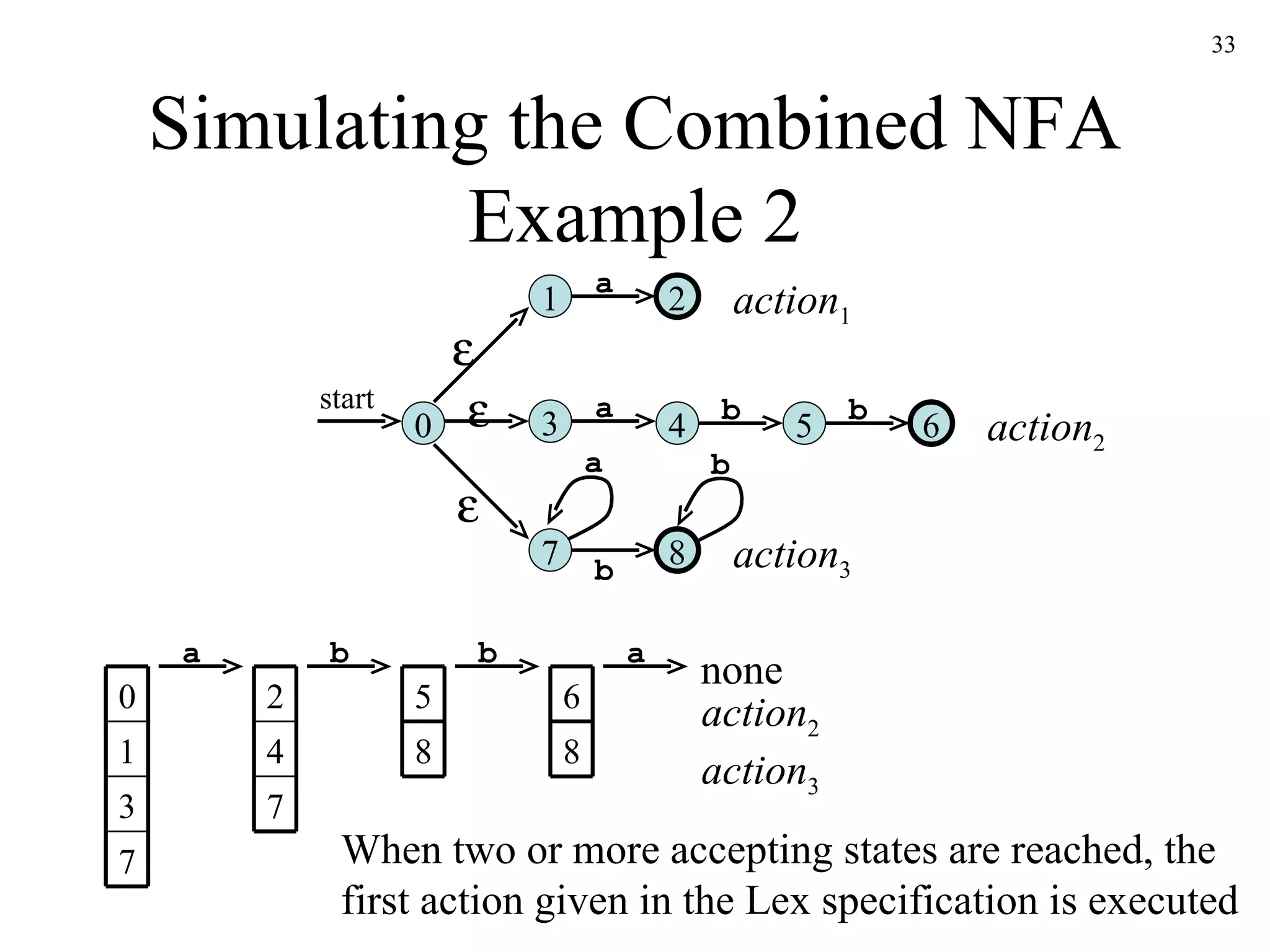
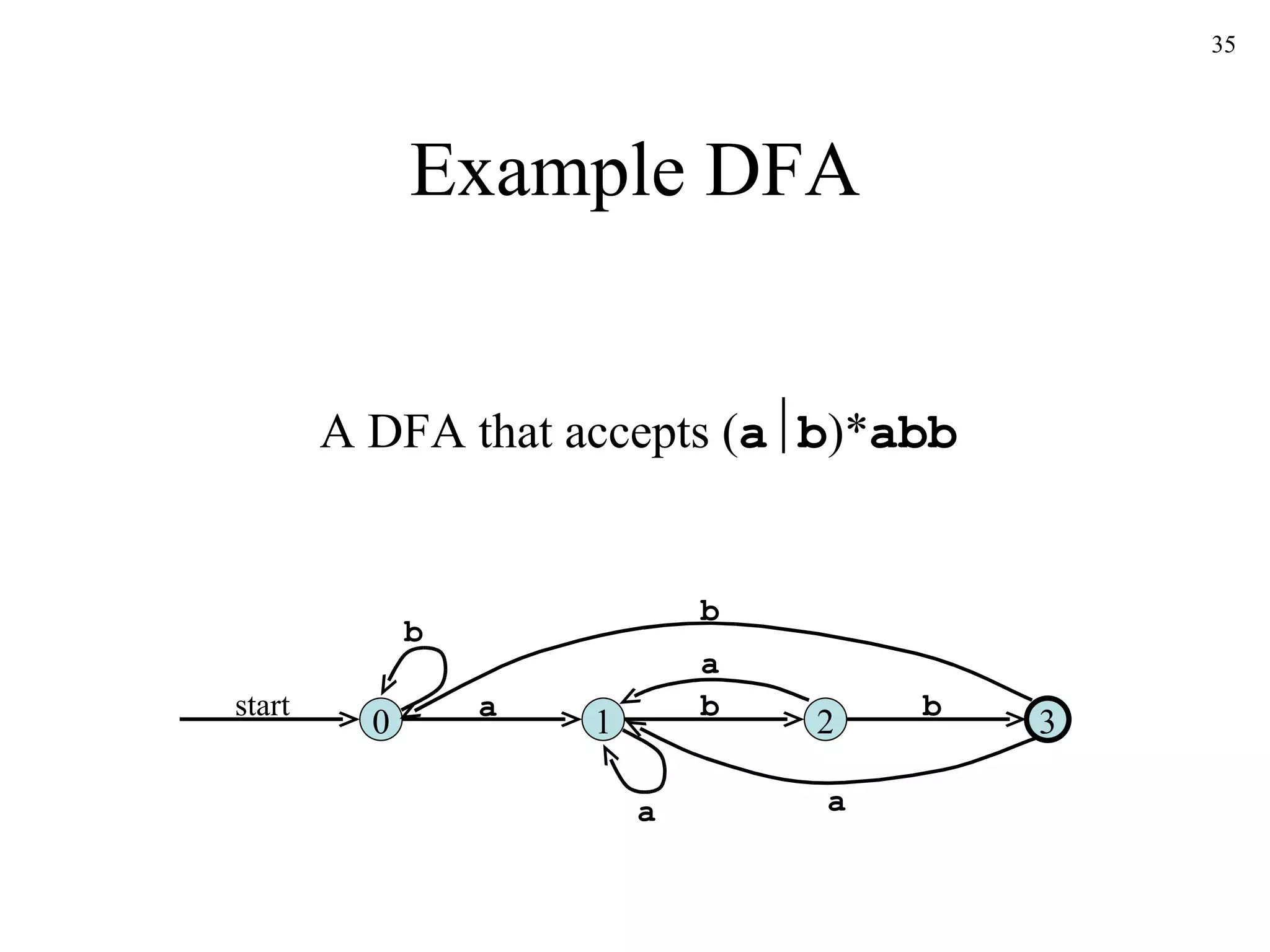
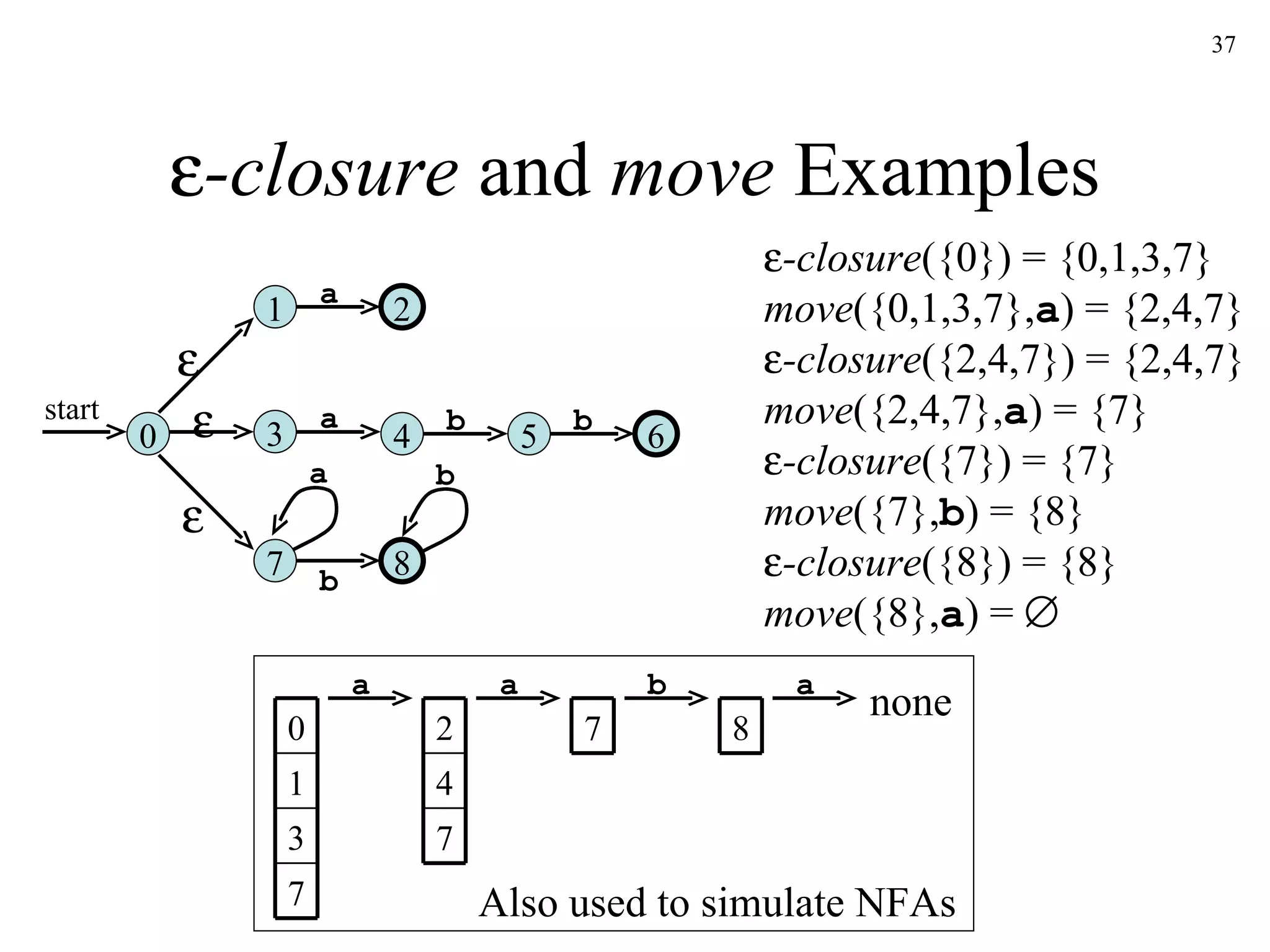
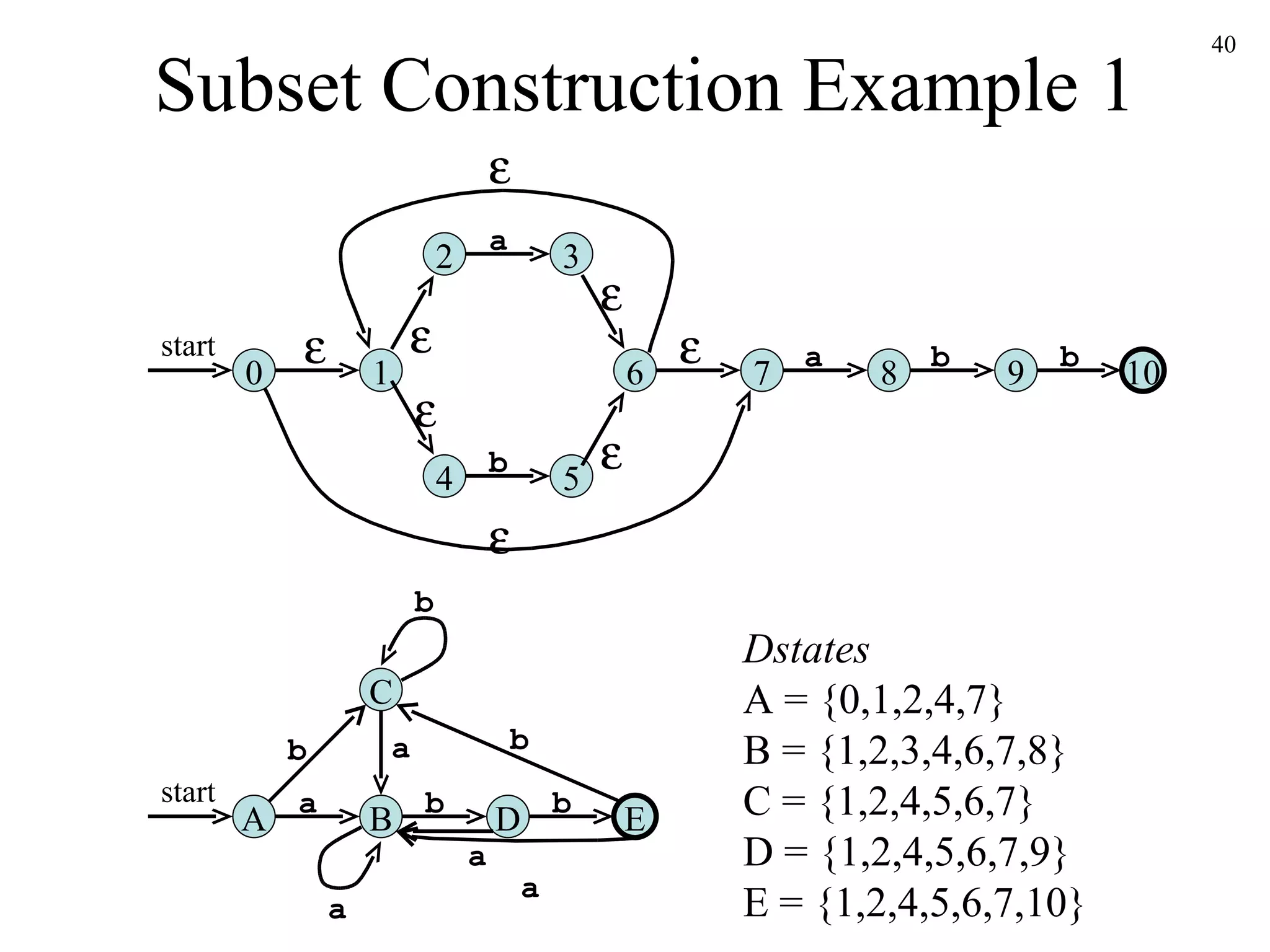
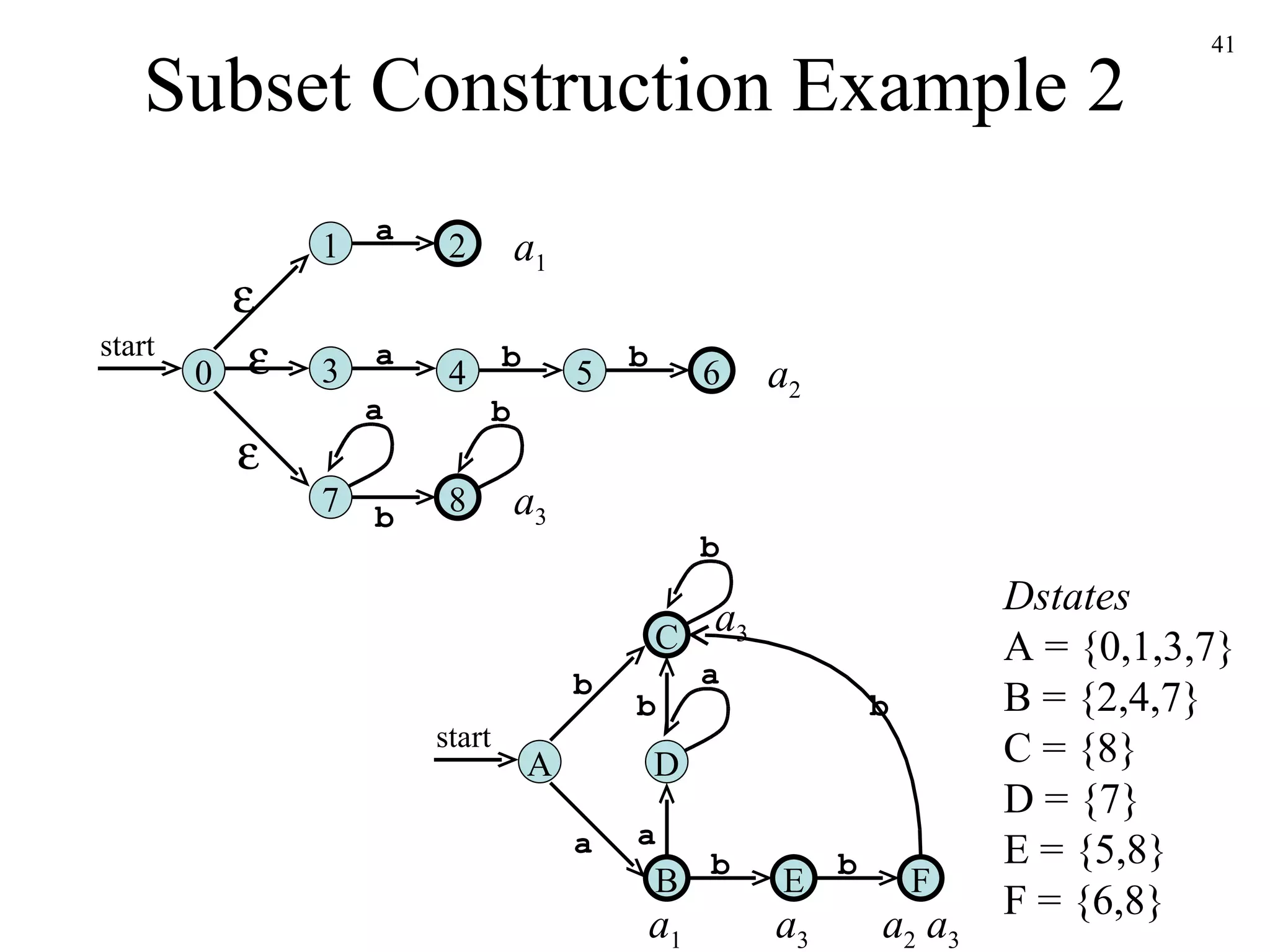
39. The Subset Construction Algorithm Initially,  -closure ( s 0 ) is the only state in Dstates and it is unmarked while there is an unmarked state T in Dstates do mark T for each input symbol a   do U :=  -closure ( move ( T,a )) if U is not in Dstates then add U as an unmarked state to Dstates end if Dtran [ T , a ] := U end do end do

40. Subset Construction Example 1 0 start a 1 10 2 b b a b 3 4 5 6 7 8 9         A start B C D E b b b b b a a a a Dstates A = {0,1,2,4,7} B = {1,2,3,4,6,7,8} C = {1,2,4,5,6,7} D = {1,2,4,5,6,7,9} E = {1,2,4,5,6,7,10} a

41. Subset Construction Example 2 2 a 1 6 a 3 4 5 b b 8 b 7 a b 0 start    a 1 a 2 a 3 Dstates A = {0,1,3,7} B = {2,4,7} C = {8} D = {7} E = {5,8} F = {6,8} A start a D b b b a b b B C E F a b a 1 a 3 a 3 a 2 a 3

42. Minimizing the Number of States of a DFA A start B C D E b b b b b a a a a a A start B D E b b a a b a a

43. From Regular Expression to DFA Directly The “ important states” of an NFA are those without an  -transition, that is if move ({ s }, a )   for some a then s is an important state The subset construction algorithm uses only the important states when it determines  -closure ( move ( T,a ))

44. From Regular Expression to DFA Directly (Algorithm) Augment the regular expression r with a special end symbol # to make accepting states important: the new expression is r # Construct a syntax tree for r # Traverse the tree to construct functions nullable , firstpos , lastpos , and followpos

45. From Regular Expression to DFA Directly: Syntax Tree of ( a | b )* abb# * | 1 a 2 b 3 a 4 b 5 b # 6 concatenation closure alternation position number (for leafs  )

46. From Regular Expression to DFA Directly: Annotating the Tree nullable ( n ): the subtree at node n generates languages including the empty string firstpos ( n ): set of positions that can match the first symbol of a string generated by the subtree at node n lastpos ( n ): the set of positions that can match the last symbol of a string generated be the subtree at node n followpos ( i ): the set of positions that can follow position i in the tree

47. From Regular Expression to DFA Directly: Annotating the Tree Node n nullable ( n ) firstpos ( n ) lastpos ( n ) Leaf  true   Leaf i false { i } { i } | / \ c 1 c 2 nullable ( c 1 ) or nullable ( c 2 ) firstpos ( c 1 )  firstpos ( c 2 ) lastpos ( c 1 )  lastpos ( c 2 ) • / \ c 1 c 2 nullable ( c 1 ) and nullable ( c 2 ) if nullable ( c 1 ) then firstpos ( c 1 )  firstpos ( c 2 ) else firstpos ( c 1 ) if nullable ( c 2 ) then lastpos ( c 1 )  lastpos ( c 2 ) else lastpos ( c 2 ) * | c 1 true firstpos ( c 1 ) lastpos ( c 1 )

48. From Regular Expression to DFA Directly: Syntax Tree of ( a | b )* abb# {6} {1, 2, 3} {5} {1, 2, 3} {4} {1, 2, 3} {3} {1, 2, 3} {1, 2} {1, 2} * {1, 2} {1, 2} | {1} {1} a {2} {2} b {3} {3} a {4} {4} b {5} {5} b {6} {6} # nullable firstpos lastpos 1 2 3 4 5 6

49. From Regular Expression to DFA Directly: followpos for each node n in the tree do if n is a cat-node with left child c 1 and right child c 2 then for each i in lastpos ( c 1 ) do followpos ( i ) := followpos ( i )  firstpos ( c 2 ) end do else if n is a star-node for each i in lastpos ( n ) do followpos ( i ) := followpos ( i )  firstpos ( n ) end do end if end do

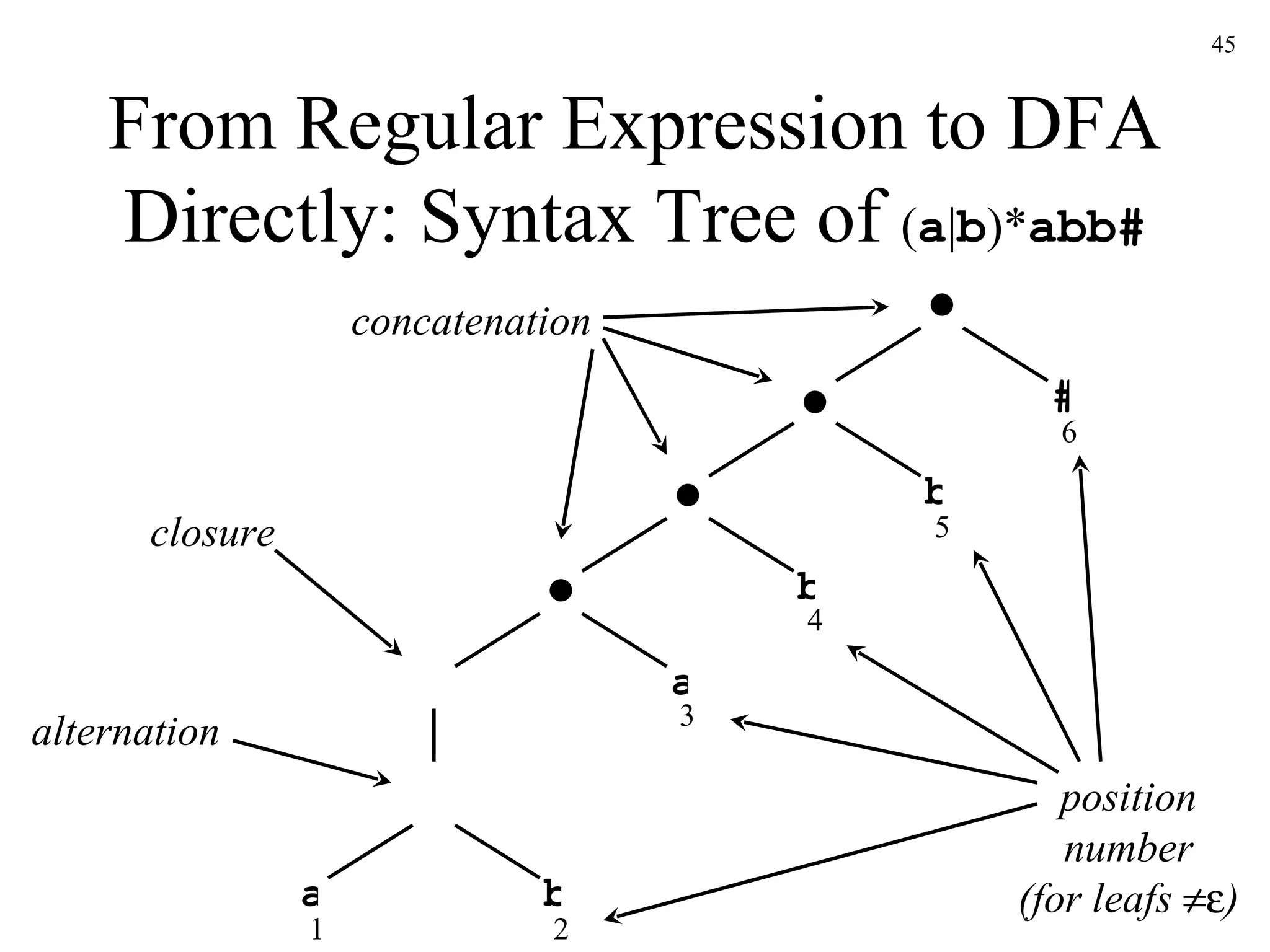
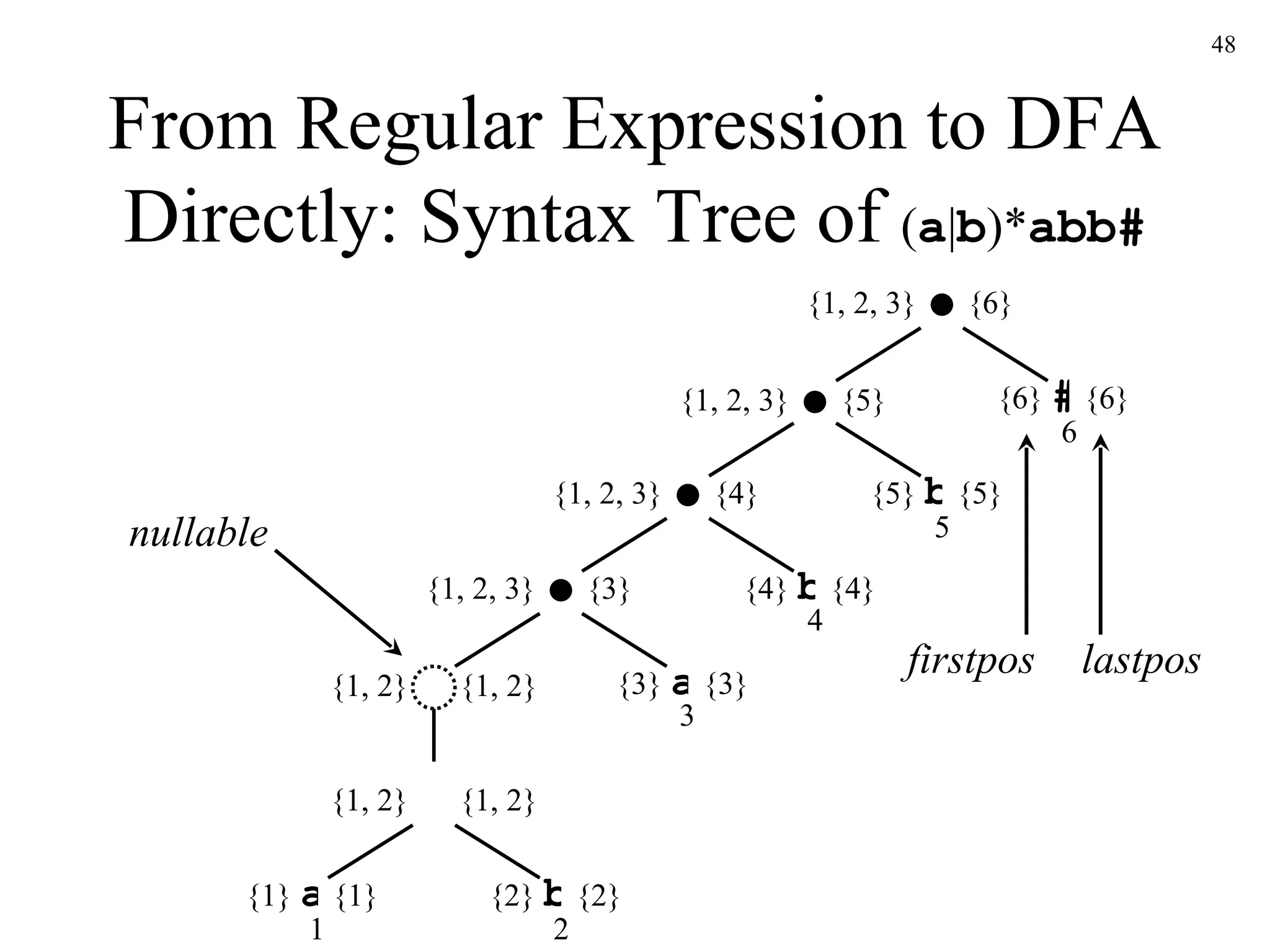
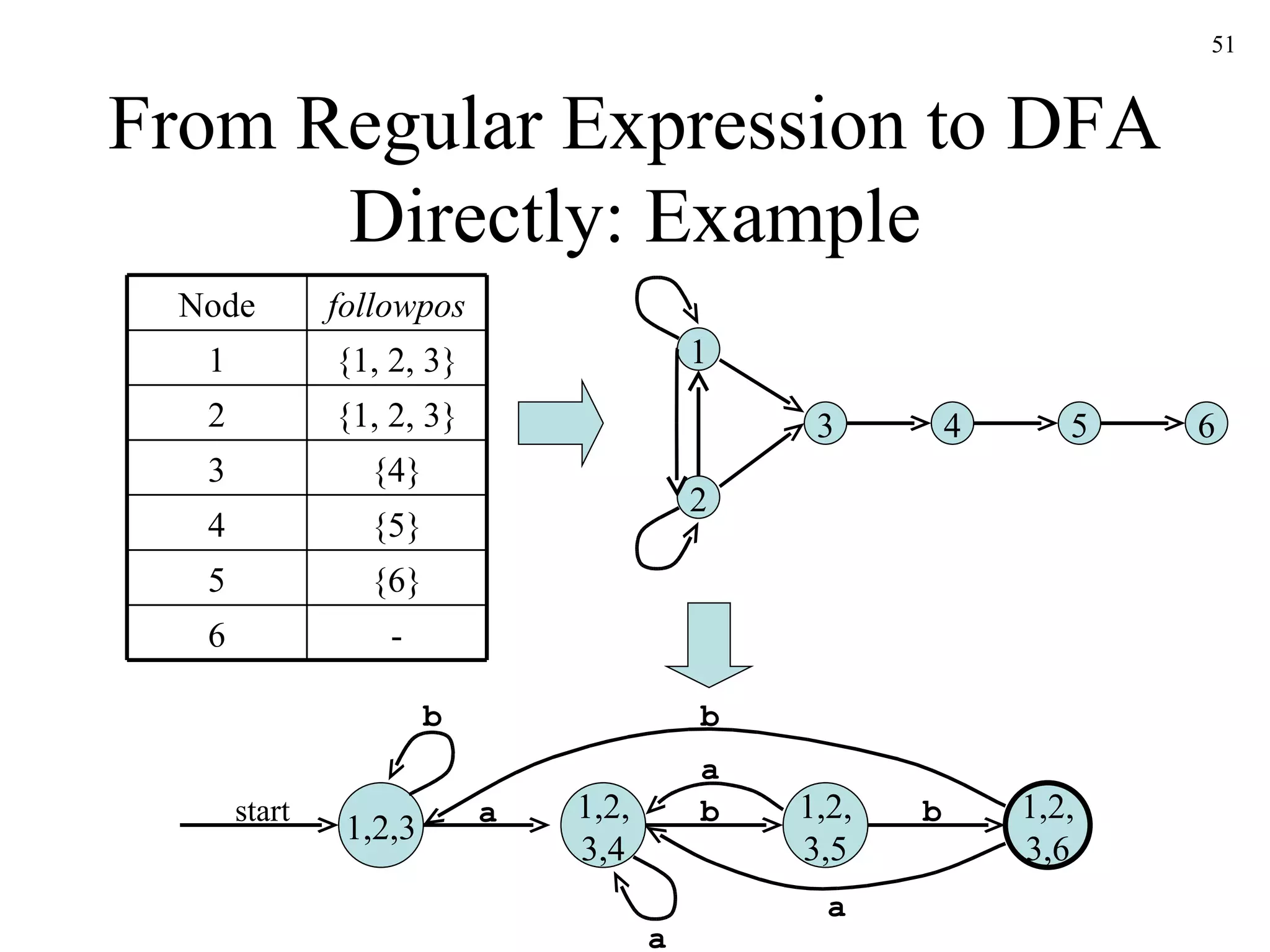
50. From Regular Expression to DFA Directly: Algorithm s 0 := firstpos ( root ) where root is the root of the syntax tree Dstates := { s 0 } and is unmarked while there is an unmarked state T in Dstates do mark T for each input symbol a   do let U be the set of positions that are in followpos ( p ) for some position p in T , such that the symbol at position p is a if U is not empty and not in Dstates then add U as an unmarked state to Dstates end if Dtran [ T,a ] := U end do end do

51. From Regular Expression to DFA Directly: Example 1,2,3 start a 1,2, 3,4 1,2, 3,6 1,2, 3,5 b b b b a a a 1 2 3 4 5 6 Node followpos 1 {1, 2, 3} 2 {1, 2, 3} 3 {4} 4 {5} 5 {6} 6 -

52. Time-Space Tradeoffs Automaton Space (worst case) Time (worst case) NFA O (  r  ) O (  r  x  ) DFA O (2 | r | ) O (  x  )