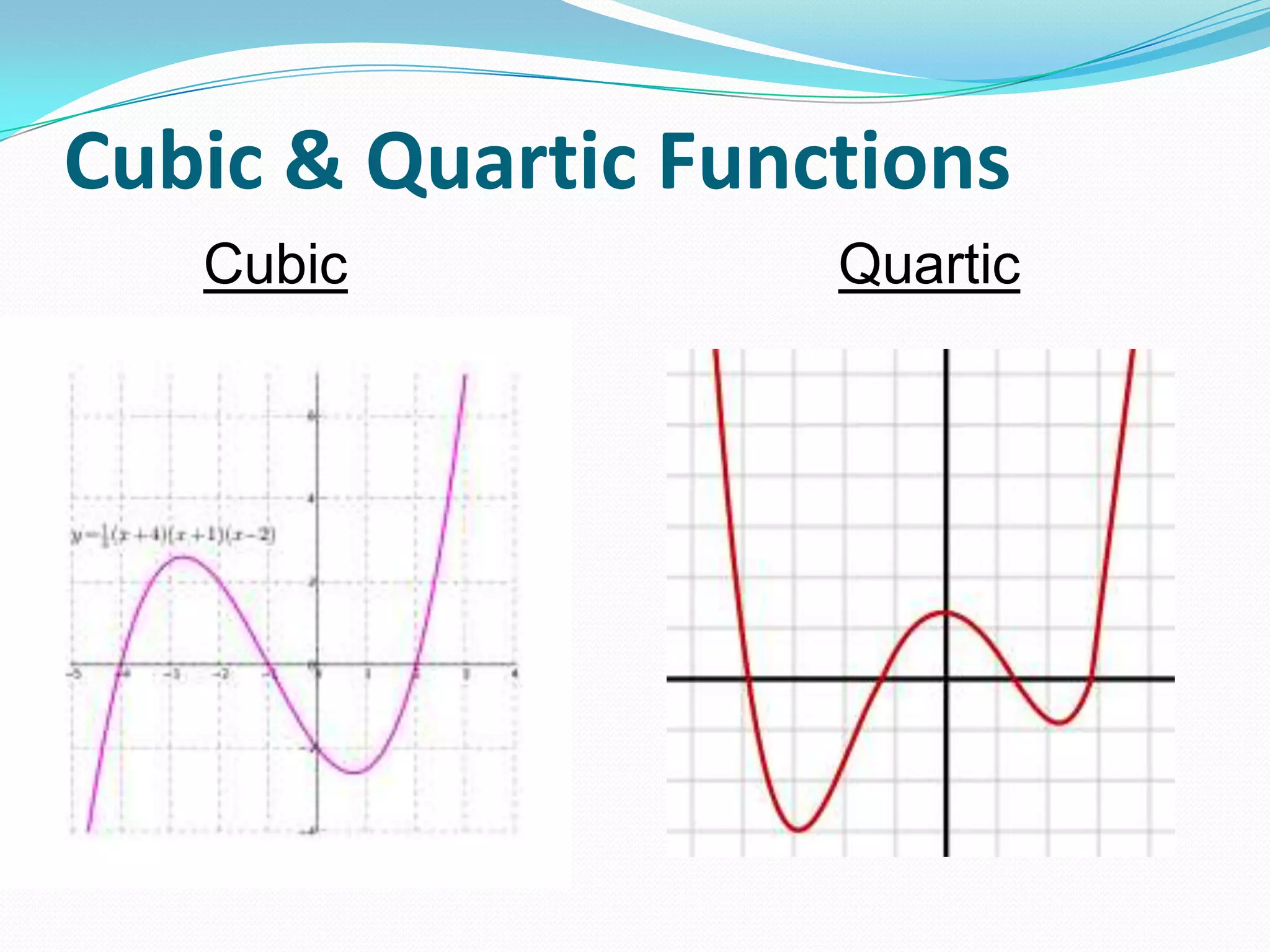
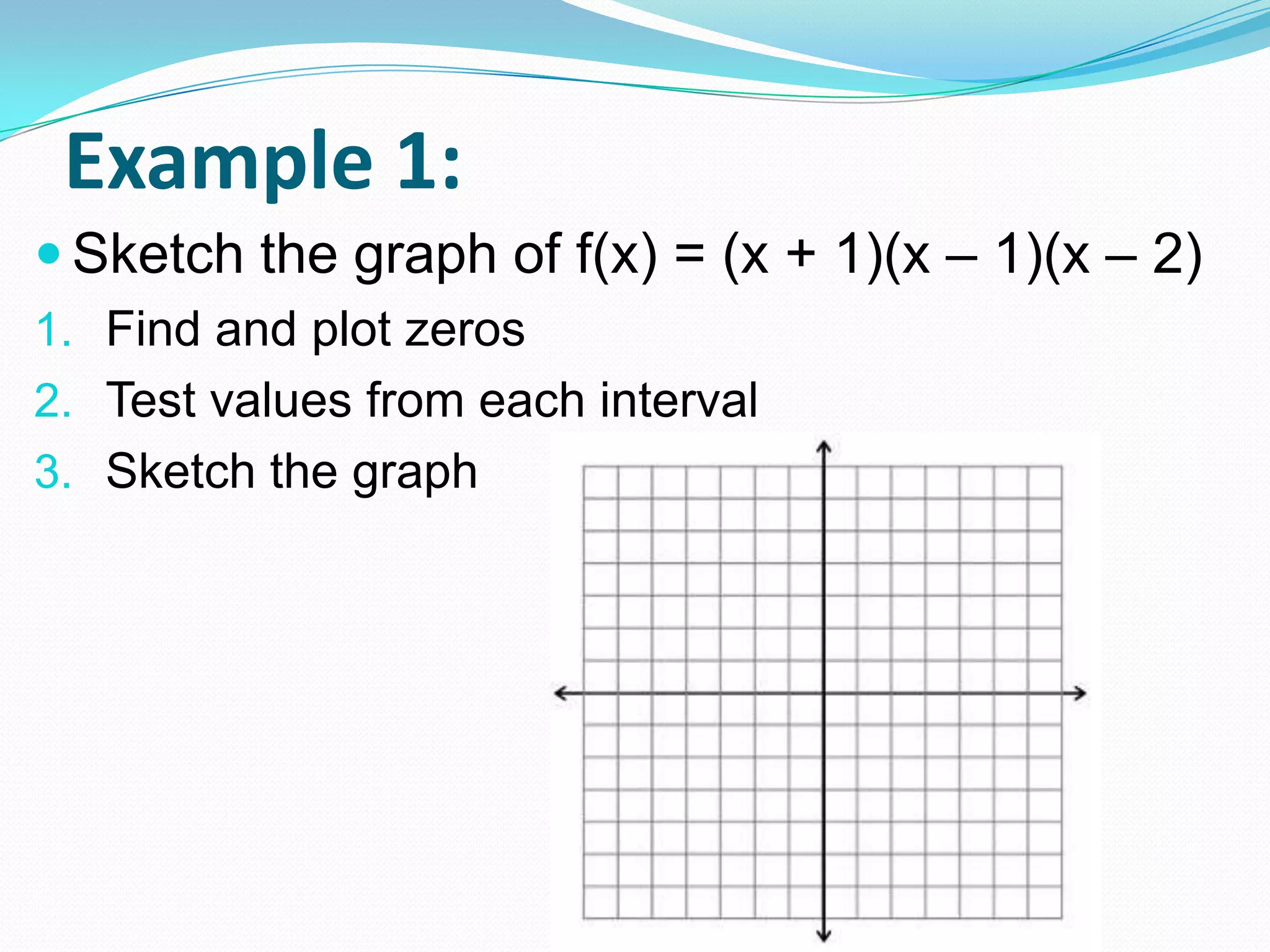
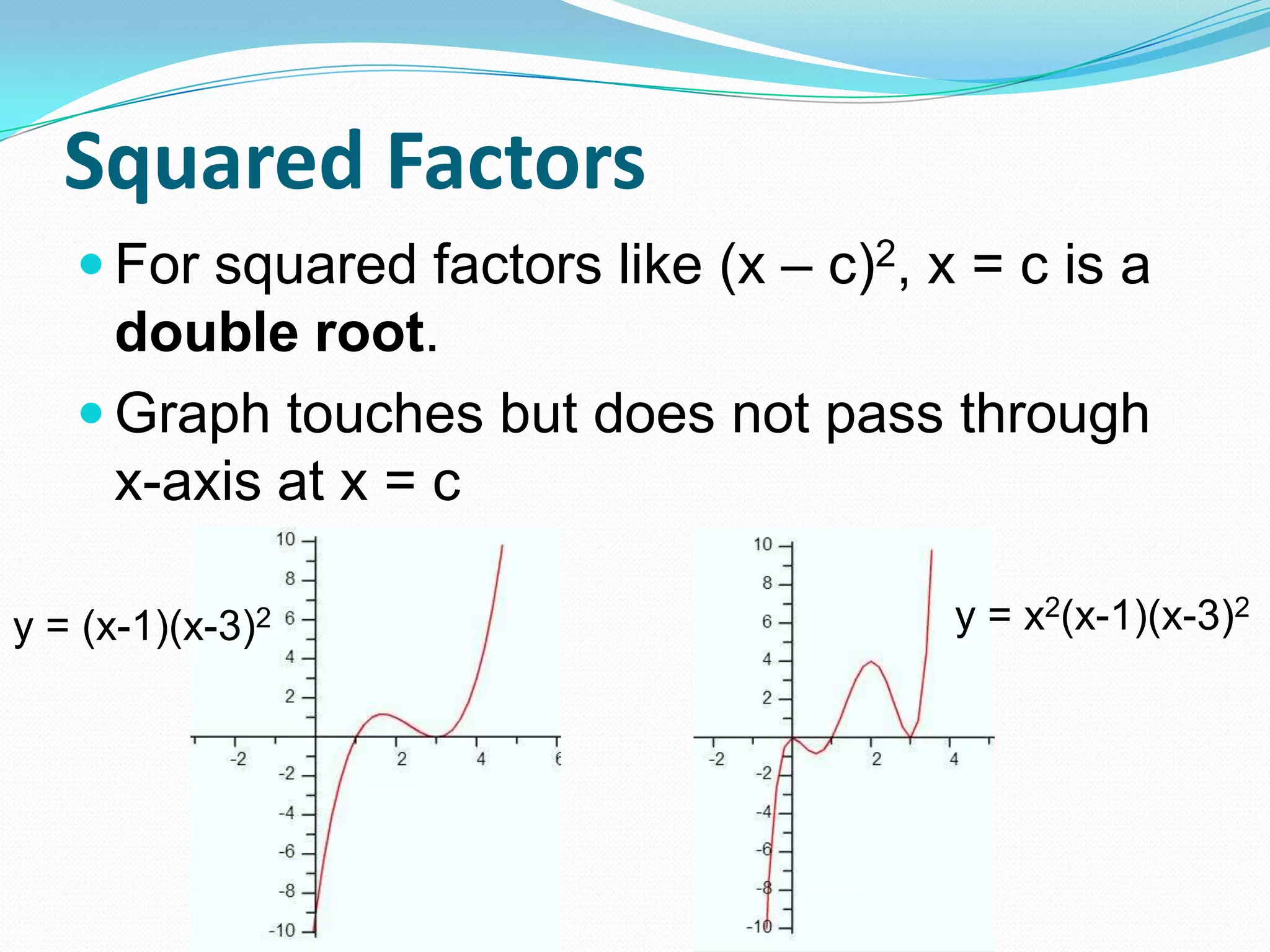
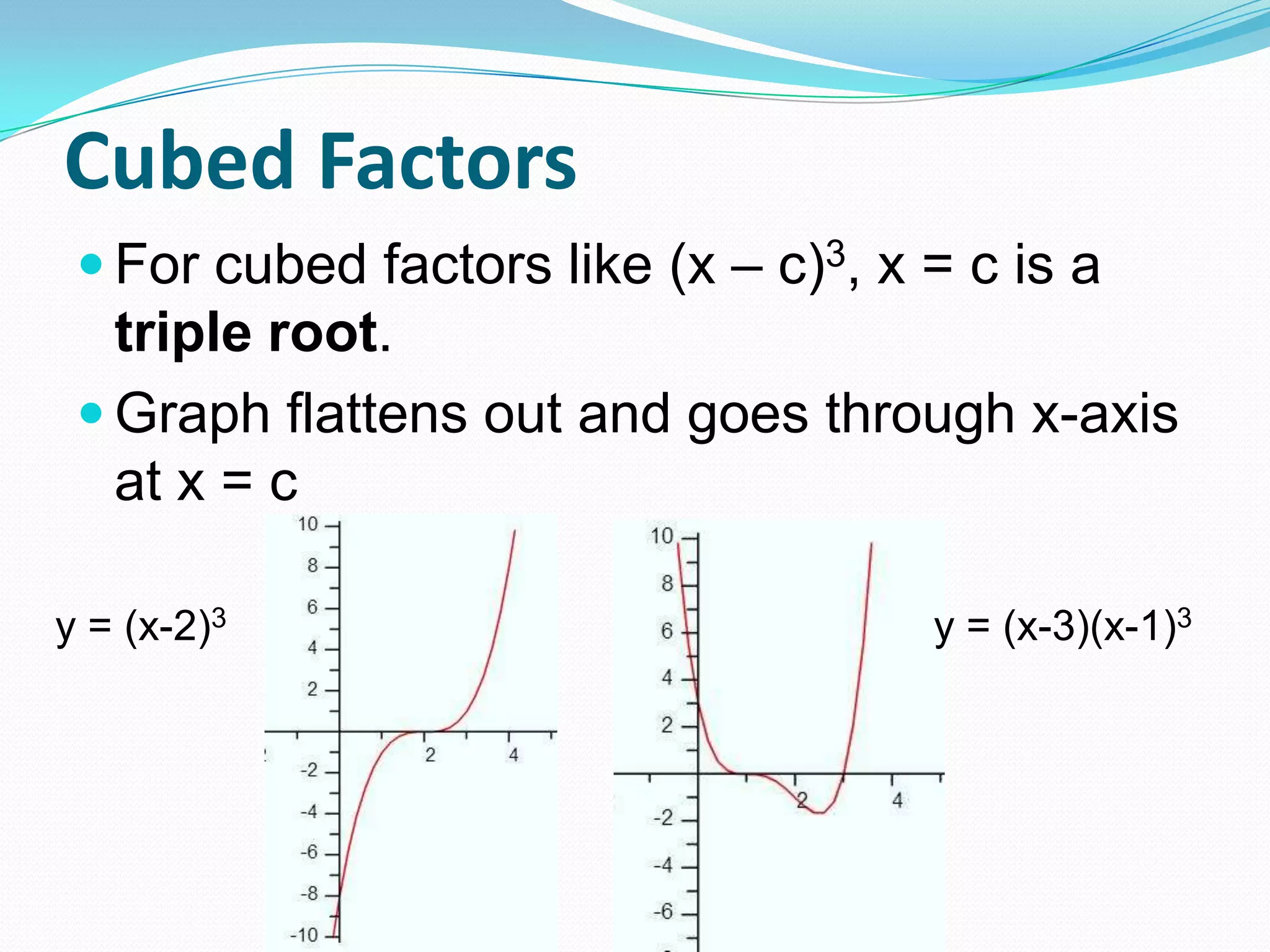
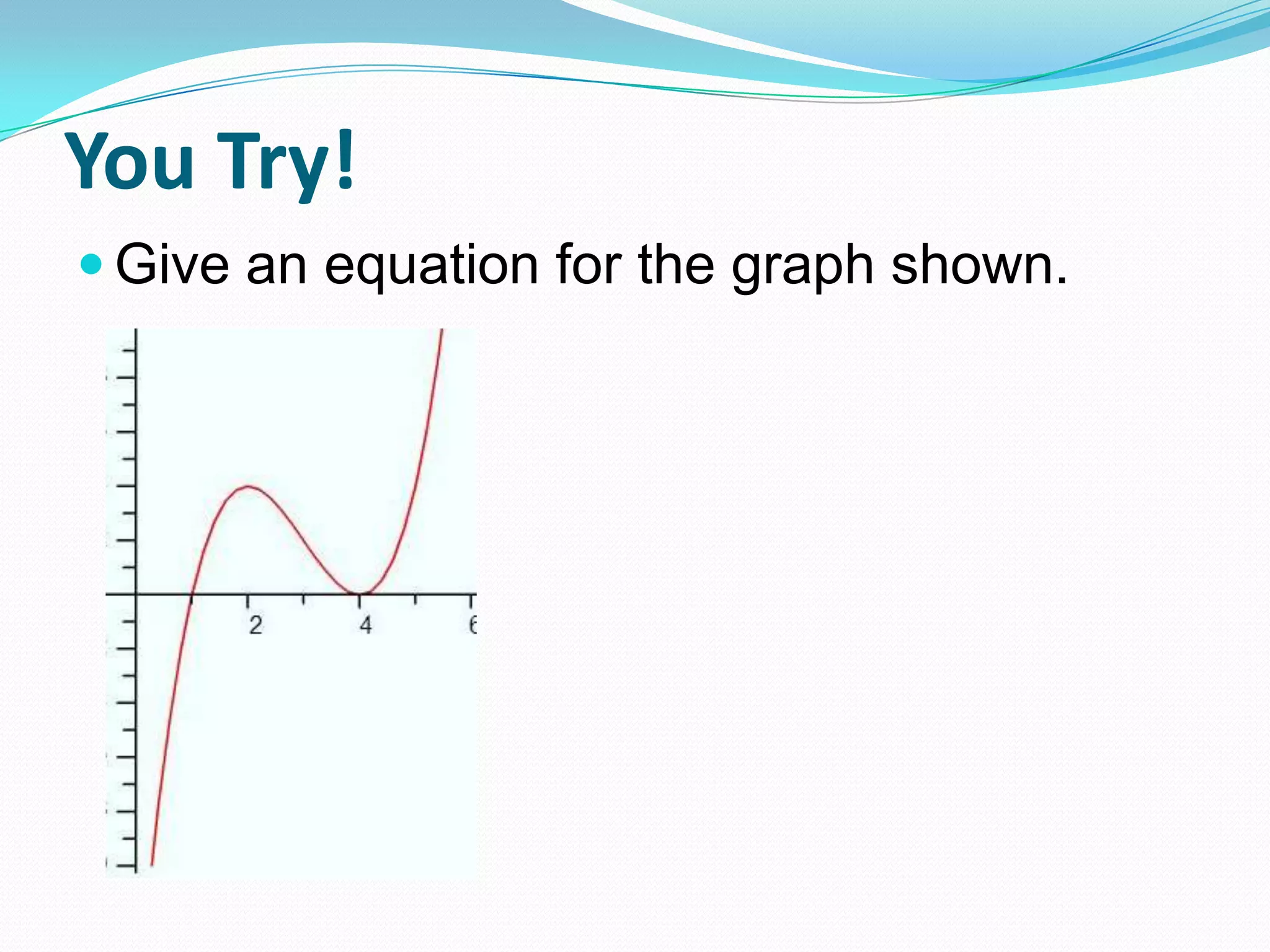
This document discusses graphing polynomials and writing polynomial equations from graphs. It provides examples of graphing polynomials with cubic and quartic factors and explains that squared factors result in a double root where the graph touches but does not pass through the x-axis, while cubed factors result in a triple root where the graph flattens out and passes through the x-axis. It also explains that the zeros from a polynomial graph can be used to write the polynomial in factored form.

1. Objectives:
1. Graph a polynomial
2. Write an equation for a polynomial graph

2. Cubic & Quartic Functions
Cubic Quartic

3. Example 1:
Sketch the graph of f(x)=(x + 1)(x – 1)(x – 2)
1. Find and plot zeros
2. Test values from each interval
3. Sketch the graph

4. You Try!
Sketch the graph of
y = -(x + 3)(x + 1)(x – 1)(x – 2)

5. Squared Factors
For squared factors like (x – c)2, x = c is a
double root.
Graph touches but does not pass through
x-axis at x = c
y = (x-1)(x-3)2 y = x2(x-1)(x-3)2

6. Cubed Factors
For cubed factors like (x – c)3, x = c is a
triple root.
Graph flattens out and goes through x-axis
at x = c
y = (x-2)3 y = (x-3)(x-1)3

7. Writing Equations
Use the zeros from the graph to write an
equation in factored form.
Example:

8. You Try!
Give a possible equation for the graph
shown.