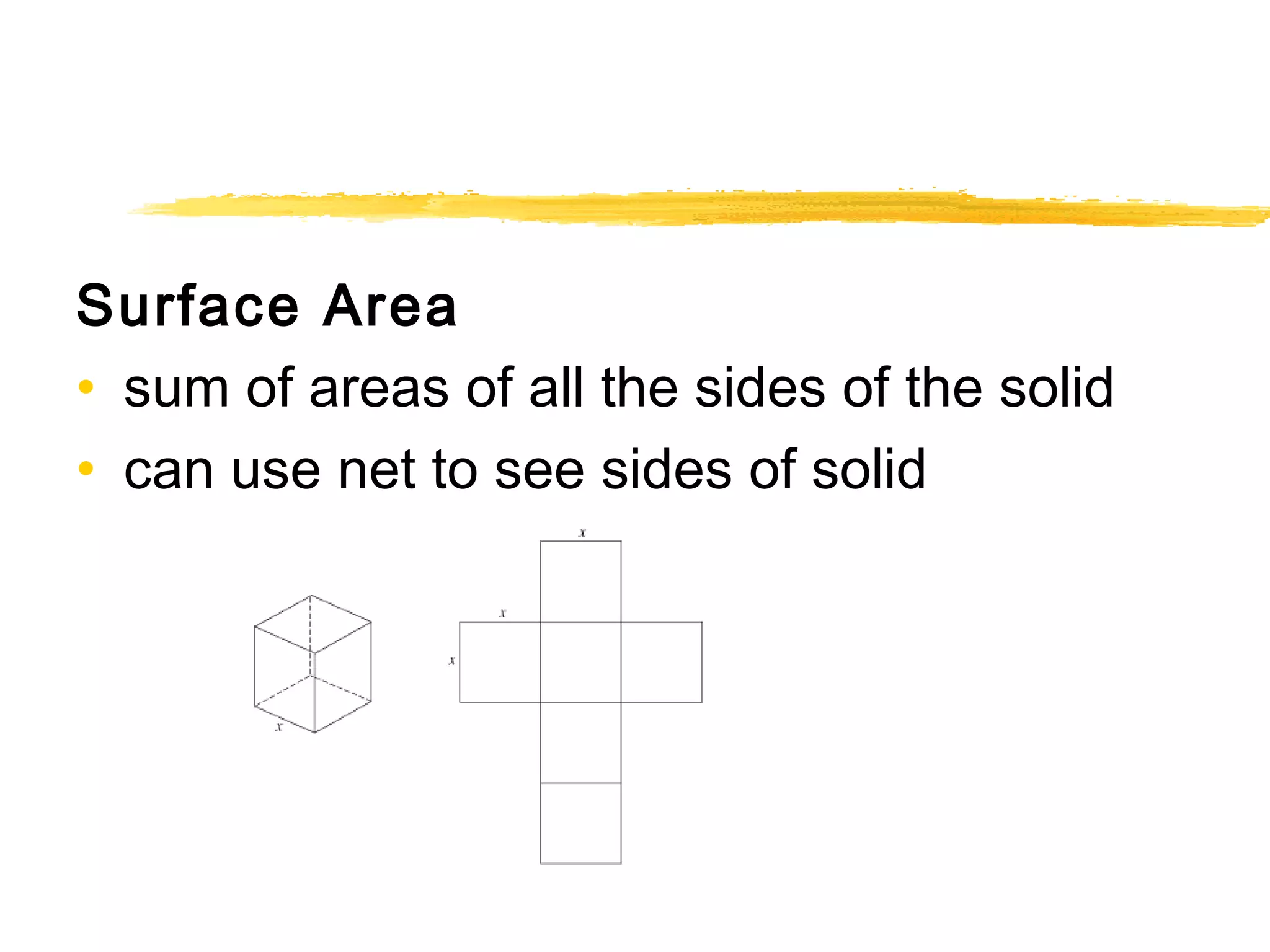
The document provides a review of key geometry and measurement concepts tested on the SAT: - It outlines topics that are not directly tested like proofs, trigonometry, and radians. - Key terms are defined for geometric figures like points, lines, angles, and their properties. - Properties of triangles, quadrilaterals, circles, and three-dimensional shapes are summarized. - Formulas for area, perimeter, volume, and surface area are presented. - Geometric perception and coordinate geometry questions are described.

1. Geometry and
Measurement Review
The SAT doesn’t include:
• Formal geometric proofs
• Trigonometry
• Radian measure

2. Geometric Notation
know:
geometric
notation for
points and
lines, line
segments,
rays, angles
and their
measures,
and lengths

3. Angles in the Plane
Vertical angles
• two opposite angles formed by two
intersecting lines
• have equal measure
Supplementary angles
• two angles whose sum is 180 degrees
Complementary angles
• two angles whose sum is 90 degrees

4. Triangles
Equilateral triangle
• all three sides are equal length
• all three angles measure 60 degrees
Isosceles triangle
• two sides are equal in length
• angles opposite the equal sides are
equal

5. Right triangle
• one right angle
• hypotenuse is side opposite right angle
• hypotenuse is longest side
• other two sides are called legs
• leg2+leg2 = hypotenuse2 (Pythagorean Theorem)

6. Special Right Triangles
30°-60°-90° triangle
• short leg = x
• long leg =
x 3
• hypotenuse = 2x
45°-45°-90° triangle
• legs are equal
• angles opposite the legs are equal
• each leg = x
• hypotenuse =
x 2

7. Congruent triangles
• all three pairs of corresponding sides
are congruent
• all three pairs of corresponding
angles are congruent
• SSS, SAS, AAS, ASA

8. Similar Triangles
• same shape
• lengths of corresponding sides are in
proportion
• all pairs of corresponding angles are
congruent
• AA

9. Triangle Inequality
• sum of the lengths of any two sides of a
triangle is greater than the length of the third
side
• When one side is length a and second side is
length b , length of third side is between la –b l
and a +b
• Ex: given sides of a , 10 and 16, third
side is greater than 6 and less than 26 V

10. Quadrilaterals
Parallelograms
• Opposite sides are congruent
• Opposite angles are congruent
• Consecutive angles are supplementary
Rectangles
• parallelogram
• all angles are right angles
• diagonals are congruent

11. Squares
• rectangle and thus also parallelogram
• all sides are congruent
• diagonal is times 2 the length of a side

12. Areas and Perimeters
Rectangle
• Area = l ´
w
• Perimeter = 2l + 2w
Square
• Area = s2
• Perimeter = 4s
Parallogram
• Area = b ´
h
• Perimeter = 2l + 2w

13. Triangle
Area = 1
•
´b´h
2
• Perimeter = sum of the three sides
Polygon
• Perimeter = sum of all the sides
Regular Polygon
• all sides are equal length
• all angles are equal measure

14. Angles in a Polygon
Sum of interior angles:
o
o
o
o
Triangle 180
Quadrilateral 360
Pentagon 540
Hexagon 720
n sides (n-2) 1´80
o

15. Circles
Diameter
• line segment that passes through the center and
has its endpoints on the circle
• all diameters in same circle are equal length
Radius
• line segment from the center of the circle to a
point on the circle
• all radii in same circle are equal length
• or 1
2r = d r = d
2

16. Central angle
• angle whose vertex is the center of a
circle and formed by two radii
Arc
• part of a circle
• measure is same as measure of central
angle that cuts the arc

17. Tangent to a circle
• a line that intersects the circle at exactly
one point
• perpendicular to the radius at the point of
tangency

18. Circumference of Circle
• distance around a circle
•
C = p d C = 2p r
Area of Circle
•
A = p r2

19. Solid Figures and
Volumes
Solid Figures
• cubes, rectangular solids, prisms, cylinders,
cones, spheres, and pyramids
• volume of a rectangular solid (V= )
• volume of a right circular cylinder
p r2h
(V= )
• Recognize these solids
l ´w´h

20. Surface Area
• sum of areas of all the sides of the solid
• can use net to see sides of solid

21. Geometric
Perception
Geometric Perception Questions
• require you to visualize a plane figure
or a solid from different views
or orientations
Example:
The wire frame above is made of three wires permanently
joined together: a red wire, a blue wire, and a green
wire. Three beads, labeled A, B, and C, are attached to
the frame so that each of them can move all around the
frame. However, none of the beads can be taken off the
frame, nor can they be moved past one another. Which
of the following configurations cannot be reached by
sliding the beads around the frame or changing the
position of the frame?

22. original figure

23. Answer:
• The configuration in (A) can be reached by sliding
each bead clockwise to the next wire piece.
• The configuration in (C) can be reached by sliding
each bead counterclockwise to the next wire piece
and then flipping the frame over.
• The configuration in (D) is reached simply by sliding
bead A clockwise to the green wire.
• The configuration in (E) comes from turning the
wire frame a third of a revolution clockwise.
• The configuration in (B) cannot be reached no
matter how you slide the beads or rotate and flip
the frame.
• The correct answer is (B).

24. Coordinate Geometry
Parallel Lines
• equal slopes
Perpendicular Lines
• product of slopes is -1
ex : 2 ´- 3 = -
1
Positive Slope
3 2
• Rises up left to right
Negative Slope
• Falls from left to right

25. Midpoint
• average of the coordinates
•
æ x + x y + y ö
çè ø¸
Distance
•
1 2 , 1 2
2 2
1 2 1 2 d = (x - x ) + ( y - y )
2 2

26. Transformations
Translation
• moves a shape without any rotation or
reflection (up, down, left, right)
Rotation
• turning an object around a point, called
the center of rotation
Reflection
• mirror image with respect to a line, which
is called the line of reflection