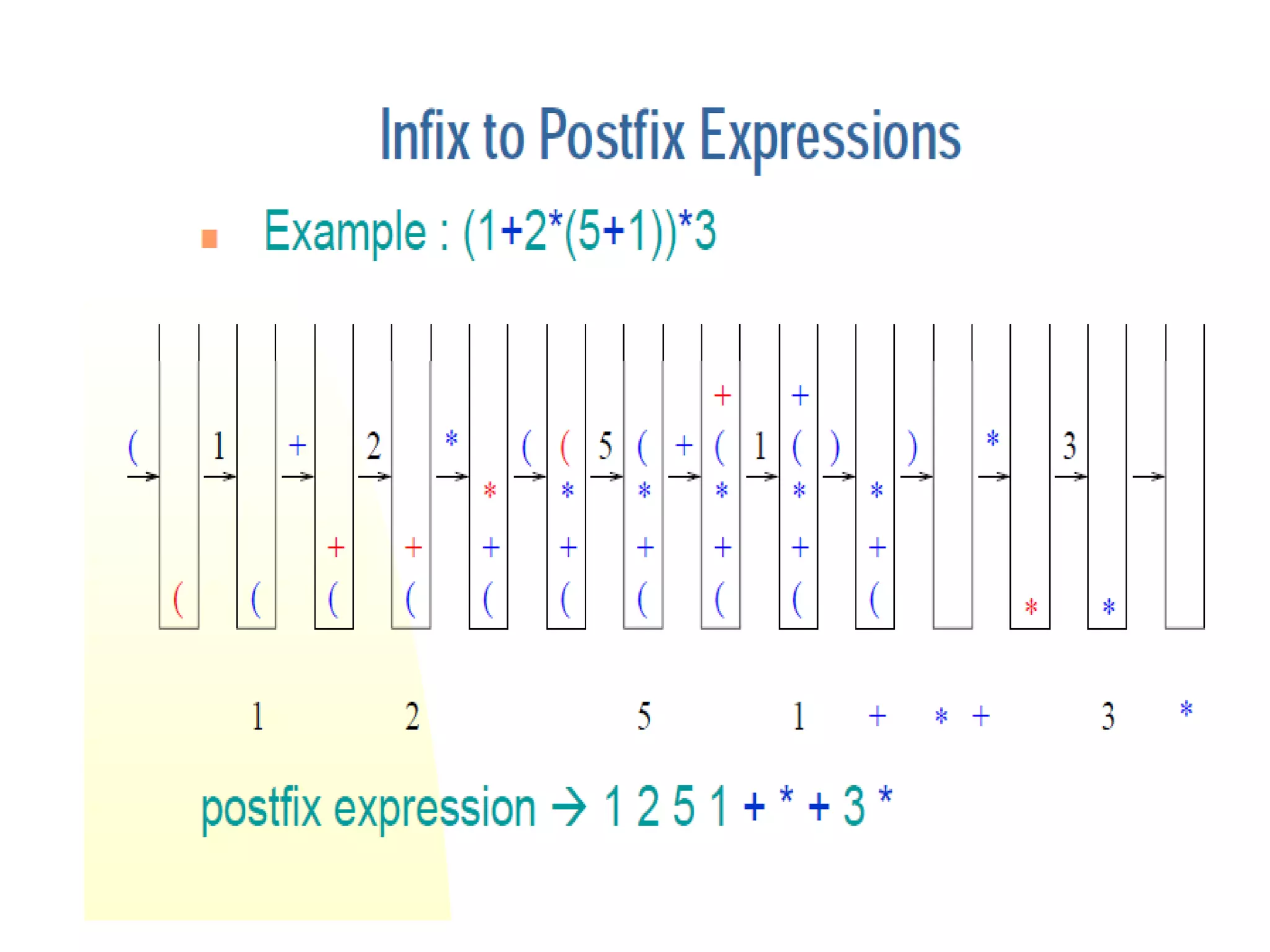
The document discusses converting expressions from infix to postfix notation. It explains that stacks are used in compilers to perform this conversion. An infix expression contains operators between operands, while a postfix expression has the operator following its operands. The algorithm scans the infix expression left to right, pushing operands and operators onto a stack based on precedence. Operators are popped off and output once higher precedence operators are encountered.

1. Infix to Postfix Conversion

2. Infix to Postfix Conversion
• Stacks are widely used in the design and implementation of
compilers.
• For example, they are used to convert arithmetic expressions
from infix notation to postfix notation.
• An infix expression is one in which operators are located
between their operands.
• In postfix notation, the operator immediately follows its
operands.

3. Precedence and Priority
Token Operator
Precedence1 Associativity
()
[]
-> .
-- ++
function call
17
array element
struct or union member
increment, decrement2 16
left-to-right
-- ++
!
-+
&*
sizeof
(type)
decrement, increment3
logical not
one’s complement
unary minus or plus
address or indirection
size (in bytes)
type cast
15
right-to-left
14
right-to-left
*/%
mutiplicative
13
Left-to-right
left-to-right

4. +-
binary add or subtract
12
left-to-right
<< >>
shift
11
left-to-right
> >=
< <=
== !=
relational
10
left-to-right
equality
9
left-to-right
&
bitwise and
8
left-to-right
^
bitwise exclusive or
7
left-to-right
bitwise or
6
left-to-right
logical and
5
left-to-right
logical or
4
left-to-right
&&

5. ?:
conditional
3
right-to-left
=
+= -= assignment
/= *= %=
<<= >>=
&= ^= 
=
2
right-to-left
,
1
left-to-right
comma

6. Examples
Infix
Postfix
2+3*4
a*b+5
(1+2)*7
a*b/c
(a/(b-c+d))*(e-a)*c
a/b-c+d*e-a*c
234*+
ab*5+
12+7*
ab*c/
abc-d+/ea-*c*
ab/c-de*ac*-

9. Algorithm
1. Scan the expression from left to right.
2. If any operands comes print it simply
3. If any operator comes compare the incoming operator with stack
operator. If the incoming operator priority is higher than stack
operator priority push the incoming operator.
4. If the incoming operator has less priority than the operator
inside the stack then go on popping the operator from top of the
stack and print them till this condition is true and then push the
incoming operator on top of the stack..
5. If both incoming and stack operator priority are equal then pop
the stack operator till this condition is true.
6. If the operator is ‘)’ then go on popping the operators from top
of the stack and print them till a matching ‘(‘ operator is found.
Delete ‘(‘ from top of the stack..

12. Suppose we want to convert 2*3/(2-1)+5*3 into Postfix form,
Expression
Stack
Output
2
Empty
2
*
*
2
3
*
23
/
/
23*
(
/(
23*
2
/(
23*2
-
/(-
23*2
1
/(-
23*21
)
/
23*21-
+
+
23*21-/
5
*
+
+*
23*21-/5
23*21-/53
3
+*
23*21-/53
Empty
23*21-/53*+
So, the Postfix Expression is 23*21-/53*+

13. Postfix Demo: The Equation
Infix: (1 + (2 * ((3 + (4 * 5)) * 6)))
= 277
Postfix: 1 2 3 4 5 * + 6 * * +
= 277
(
1
+
(
2
*
(
(
3
+
(
4
*
5
)
)
*
6
(
1
(
2
(
(
3
(
4
5
)
*
)
+
6
)
*
)
138 6 138
23 532 23
20 ** 120276
4 *++=== 277
276
1
13
2
3
4
5
*
+
6
*
*
+
)
*
)
)
)
+

14. Postfix Demo: The Stack
• What is a ‘STACK’?
• At the grocery store, on the canned goods aisle, the cans are
STACKED on top of each other.
•
Which one do we take to make sure the stack doesn’t
fall over?
•
How did the store worker put the cans into the
stack?
Where did he or she place the new can?
• We take the top item and we place new items on the top. So does
the computer.
• To evaluate the problem (1 + (2 * ((3 + (4 * 5)) * 6))), the computer
uses a stack and postfix notation.
1
14
2
3
4
5
*
+
6
*
*
+

15. Postfix Demo: The Evaluation
1
2
3
4
5
*
+
6
*
*
The Stack
5
6
4
20
3
138
23
2
276
1
277
4
*
5
=
20
3
+
20
=
23
23
*
6
=
138
*
138
=
276
+
276
=
277
The Answer
2
1
15
+

16. FPE Infix to Postfix
(((A+B)*(C-E))/(F+G))
• stack: <empty>
• output: []

17. FPE Infix to Postfix
((A+B)*(C-E))/(F+G))
• stack: (
• output: []

18. FPE Infix to Postfix
(A+B)*(C-E))/(F+G))
• stack: ( (
• output: []

19. FPE Infix to Postfix
A+B)*(C-E))/(F+G))
• stack: ( ( (
• output: []

20. FPE Infix to Postfix
+B)*(C-E))/(F+G))
• stack: ( ( (
• output: [A]

21. FPE Infix to Postfix
B)*(C-E))/(F+G))
• stack: ( ( ( +
• output: [A]

22. FPE Infix to Postfix
)*(C-E))/(F+G))
• stack: ( ( ( +
• output: [A B]

23. FPE Infix to Postfix
*(C-E))/(F+G))
• stack: ( (
• output: [A B + ]

24. FPE Infix to Postfix
(C-E))/(F+G))
• stack: ( ( *
• output: [A B + ]

25. FPE Infix to Postfix
C-E))/(F+G))
• stack: ( ( * (
• output: [A B + ]

26. FPE Infix to Postfix
-E))/(F+G))
• stack: ( ( * (
• output: [A B + C ]

27. FPE Infix to Postfix
E))/(F+G))
• stack: ( ( * ( • output: [A B + C ]

28. FPE Infix to Postfix
))/(F+G))
• stack: ( ( * ( • output: [A B + C E ]

29. FPE Infix to Postfix
)/(F+G))
• stack: ( ( *
• output: [A B + C E - ]

30. FPE Infix to Postfix
/(F+G))
• stack: (
• output: [A B + C E - * ]

31. FPE Infix to Postfix
(F+G))
• stack: ( /
• output: [A B + C E - * ]

32. FPE Infix to Postfix
F+G))
• stack: ( / (
• output: [A B + C E - * ]

33. FPE Infix to Postfix
+G))
• stack: ( / (
• output: [A B + C E - * F ]

34. FPE Infix to Postfix
G))
• stack: ( / ( +
• output: [A B + C E - * F ]

35. FPE Infix to Postfix
))
• stack: ( / ( +
• output: [A B + C E - * F G ]

36. FPE Infix to Postfix
)
• stack: ( /
• output: [A B + C E - * F G + ]

37. FPE Infix to Postfix
• stack: <empty>
• output: [A B + C E - * F G + / ]

38. •
•
•
•
•
•
•
•
•
•
•
•
•
•
•
•
•
•
•
•
•
•
•
•
•
•
•
•
•
•
•
•
•
•
•
•
•
•
•
•
•
•
•
•
•
•
•
•
•
•
•
void infix :: convert( )
{
char opr ;
while ( *s ) {
if ( *s == ' ' || *s == 't' ) {
s++ ;
continue ;
}
if ( isdigit ( *s ) || isalpha ( *s ) )
{
while ( isdigit ( *s ) || isalpha ( *s ) )
{
*t = *s ; s++ ; t-- ;
}
}
if ( *s == ')' )
{
push ( *s ) ;
s++ ;
}
if ( *s == '*' || *s == '+' || *s == '/' || *s == '%' || *s == '-' || *s == '$' )
{
if ( top != -1 )
{
opr = pop( ) ;
while ( priority ( opr ) > priority ( *s ) )
{
*t = opr ;
t-- ;
opr = pop( ) ;
}
push ( opr ) ;
push ( *s ) ;
}
else
push ( *s ) ;
s++ ;
}
if ( *s == '(' )
{
opr = pop( ) ;
while ( ( opr ) != ')' )
{
*t = opr ;
t-- ;
opr = pop ( ) ;
}
s++ ;
}
}
while ( top != -1 ) { opr = pop( ) ; *t = opr ; t-- ; } t++ ; } - See more at: http://electrofriends.com/source-codes/software-programs/cpp-programs/cpp-data-structure/c-programto-convert-an-expression-from-infix-expression-to-prefix-form/#sthash.eCuEQFN6.dpuf