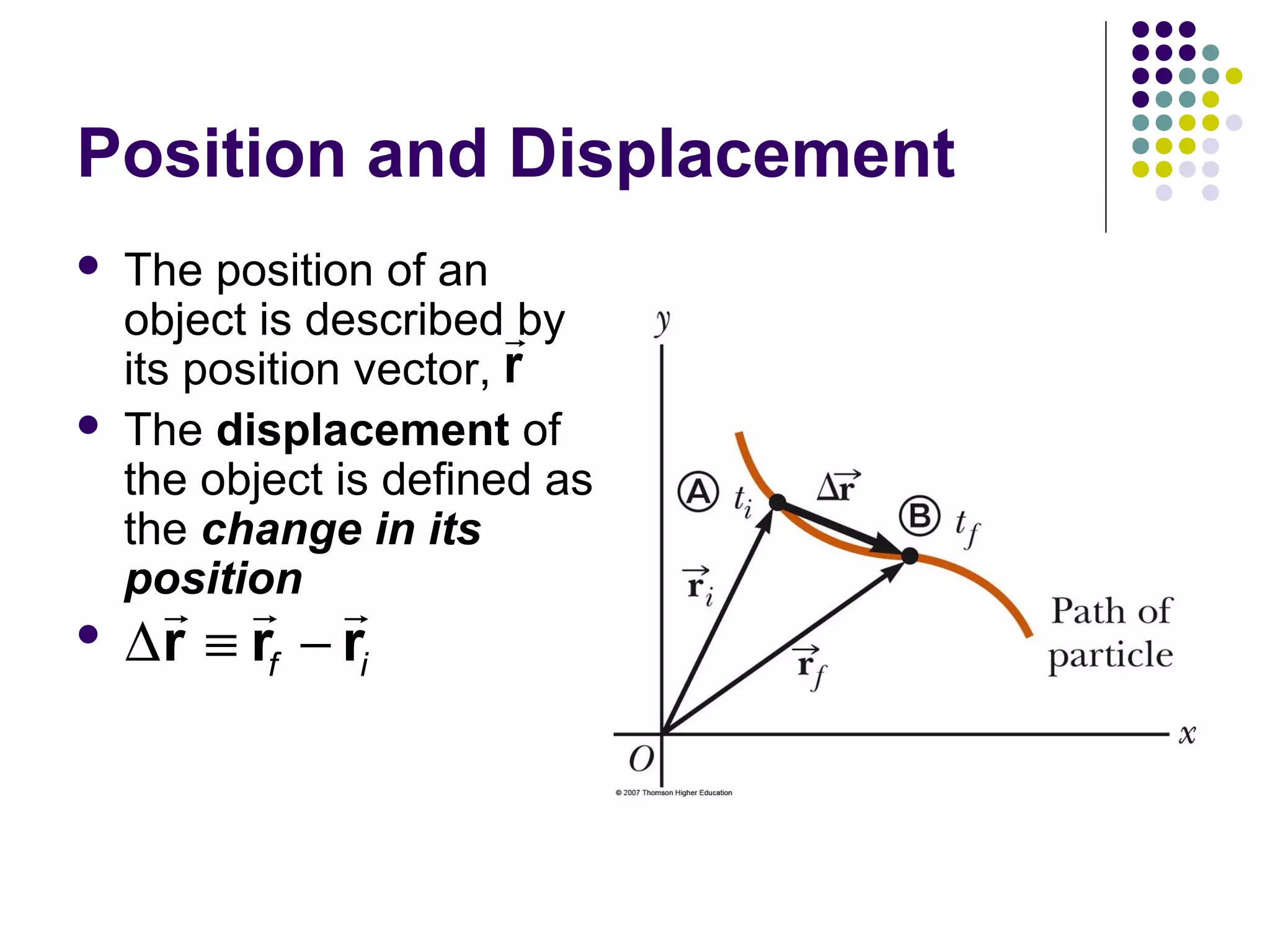
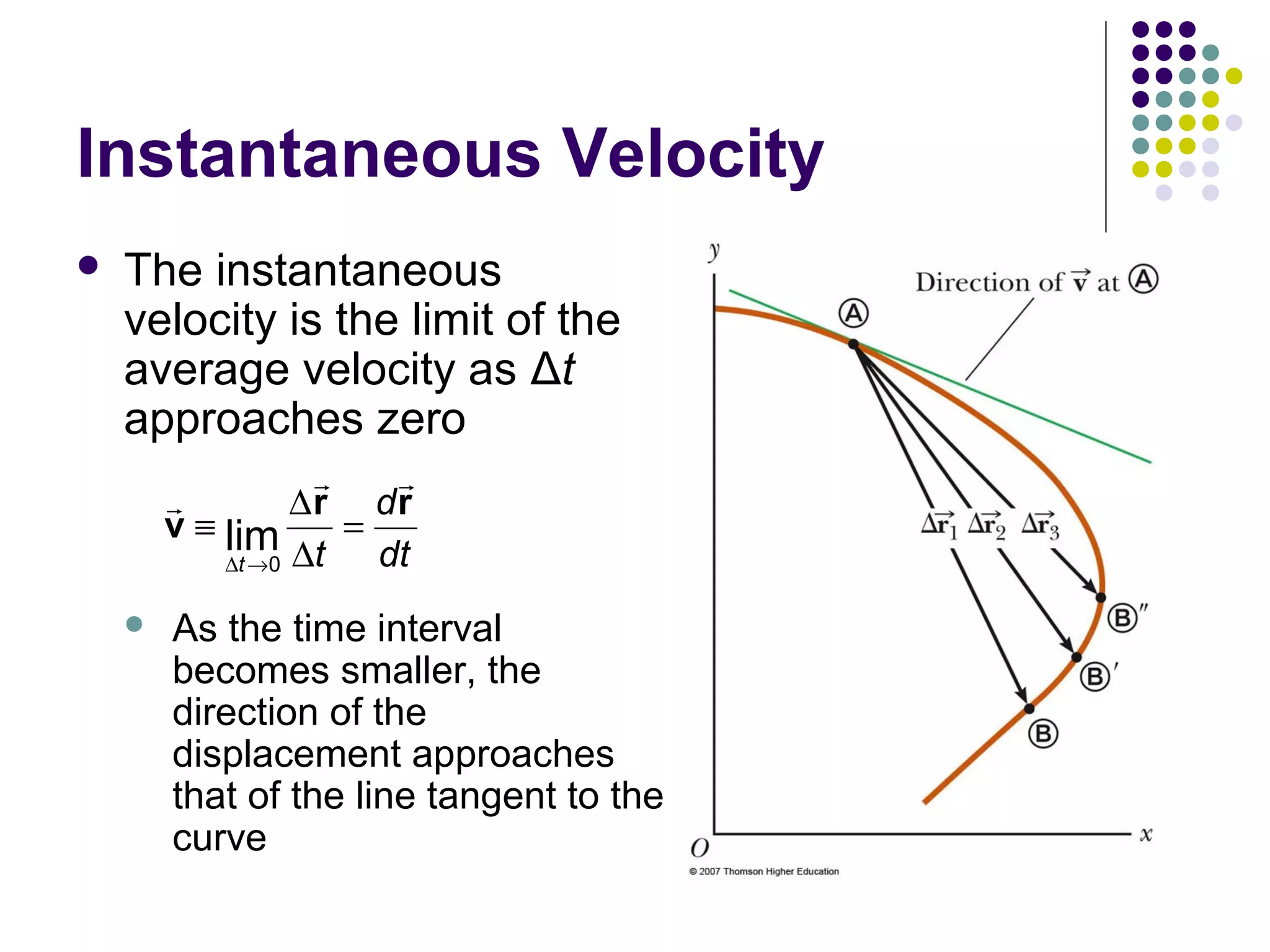
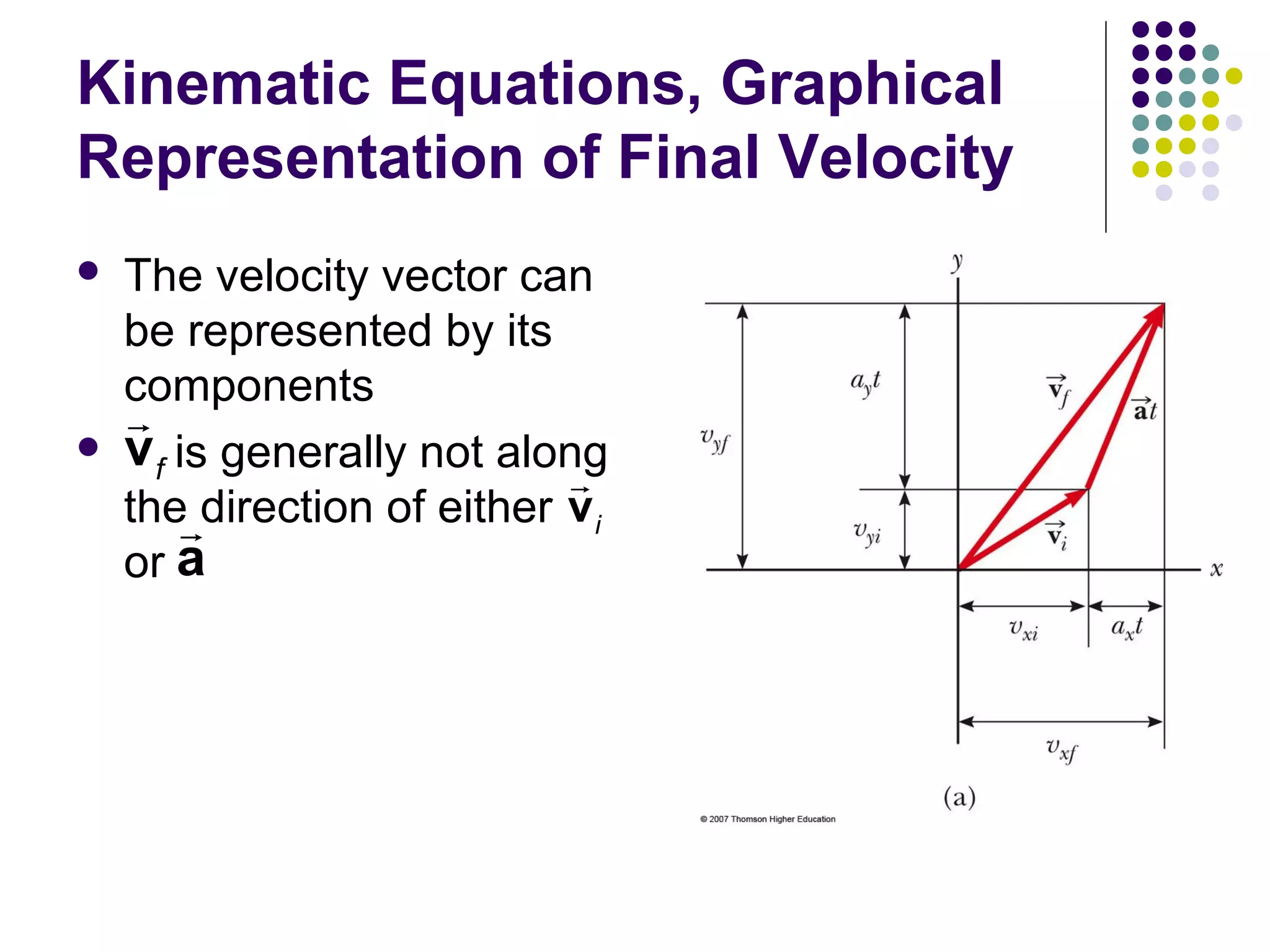
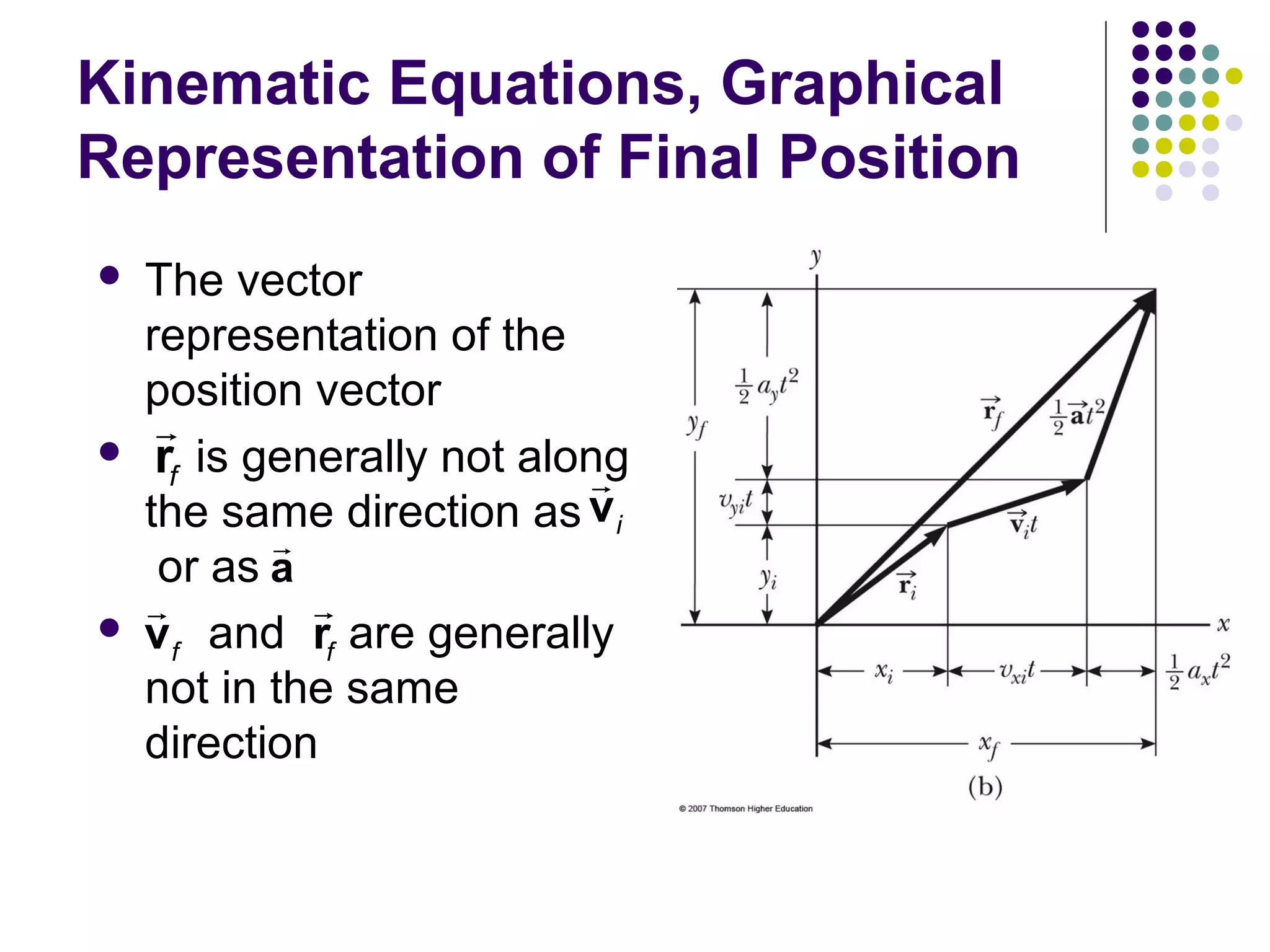
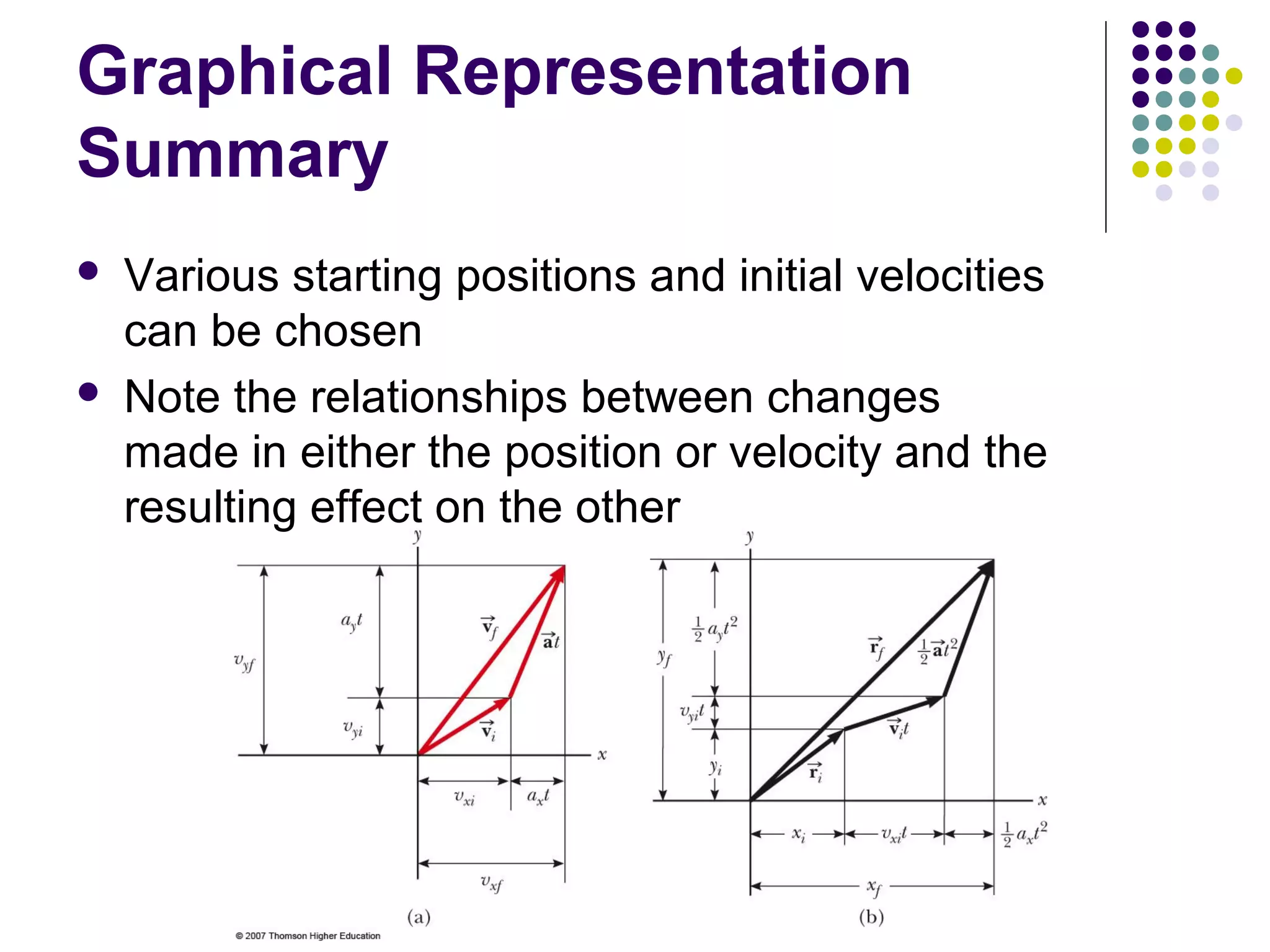
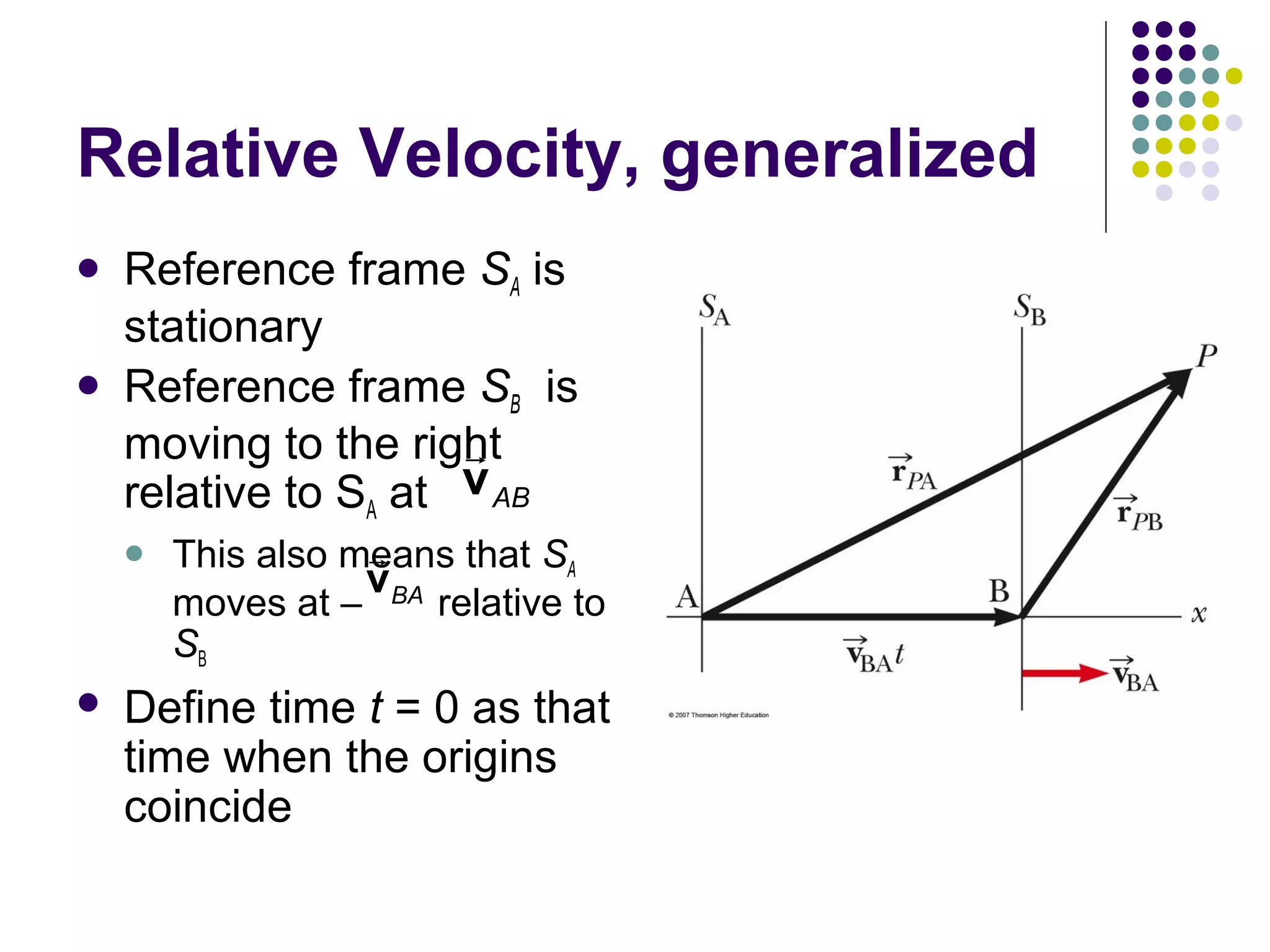
1) Motion in two dimensions can be described using vectors and involves displacement, velocity, and acceleration in both the x and y directions.
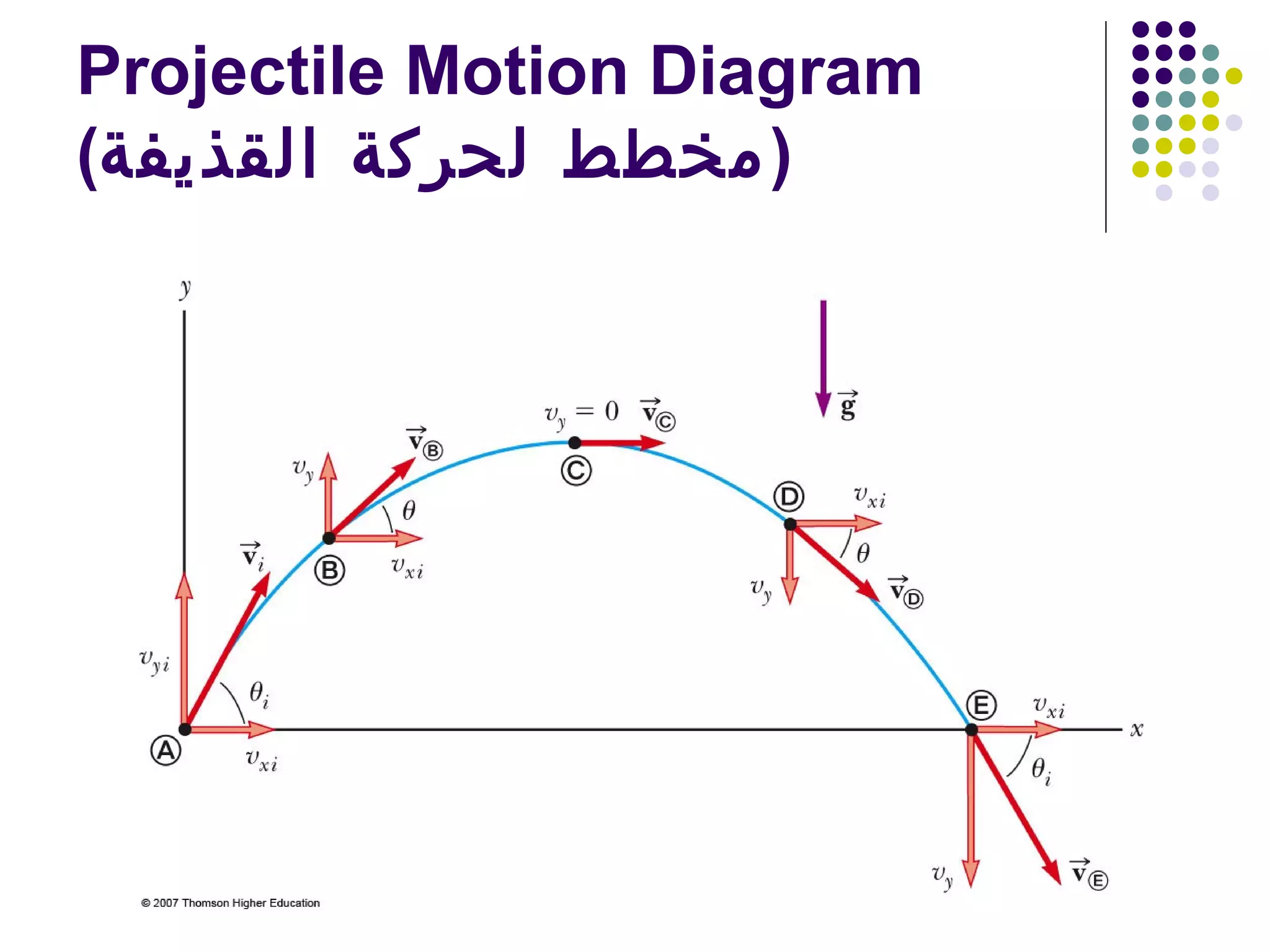
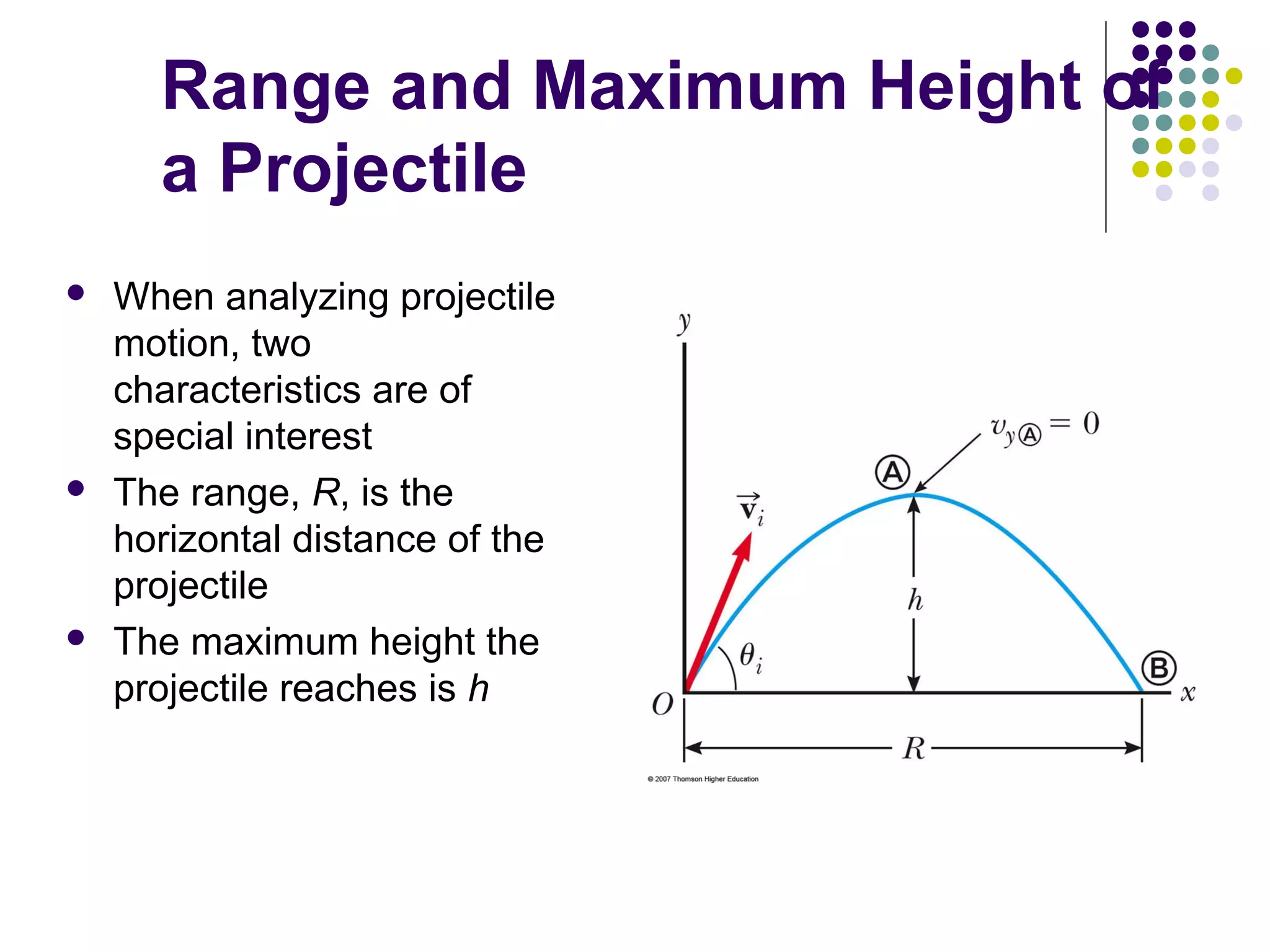
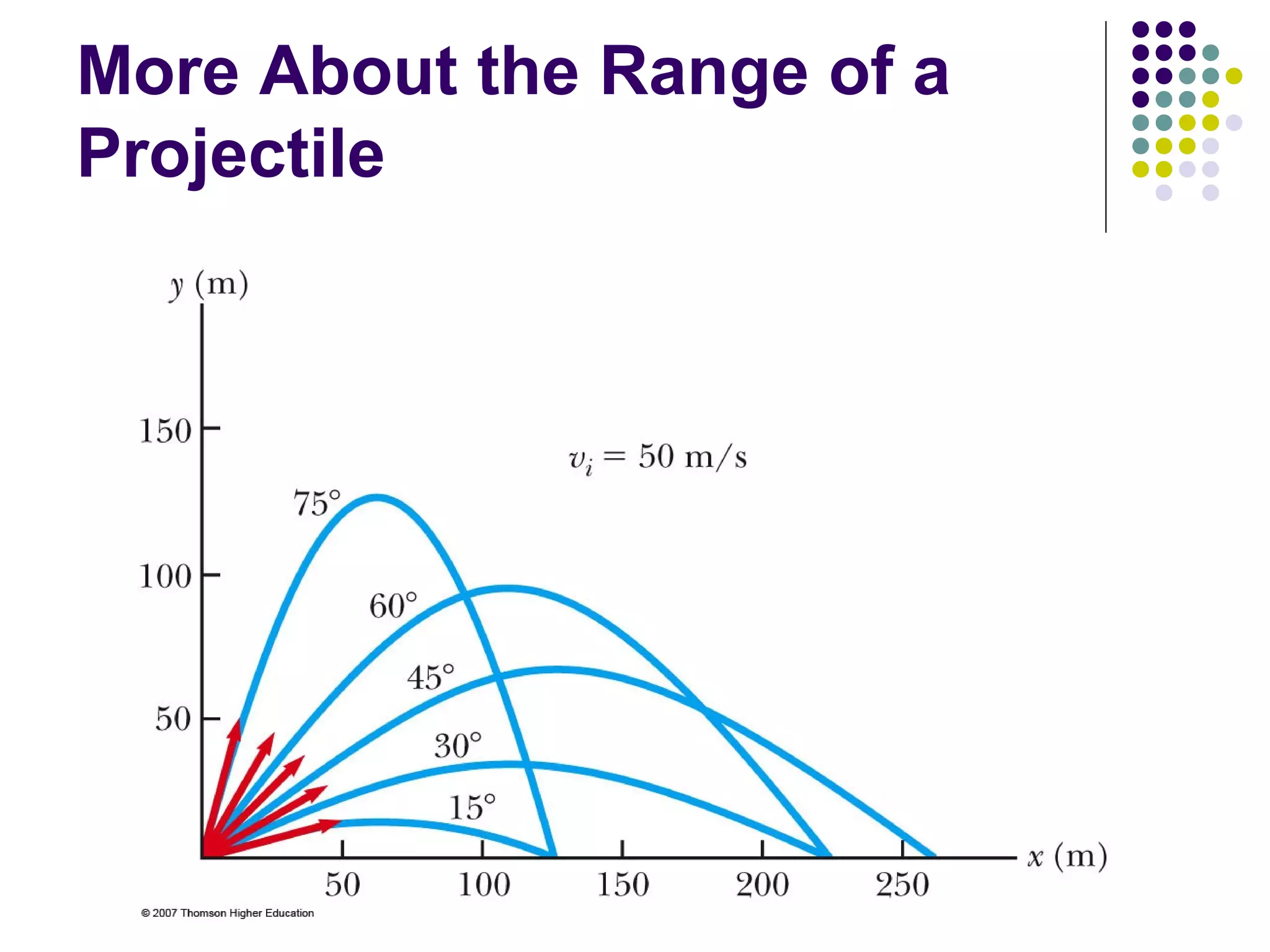
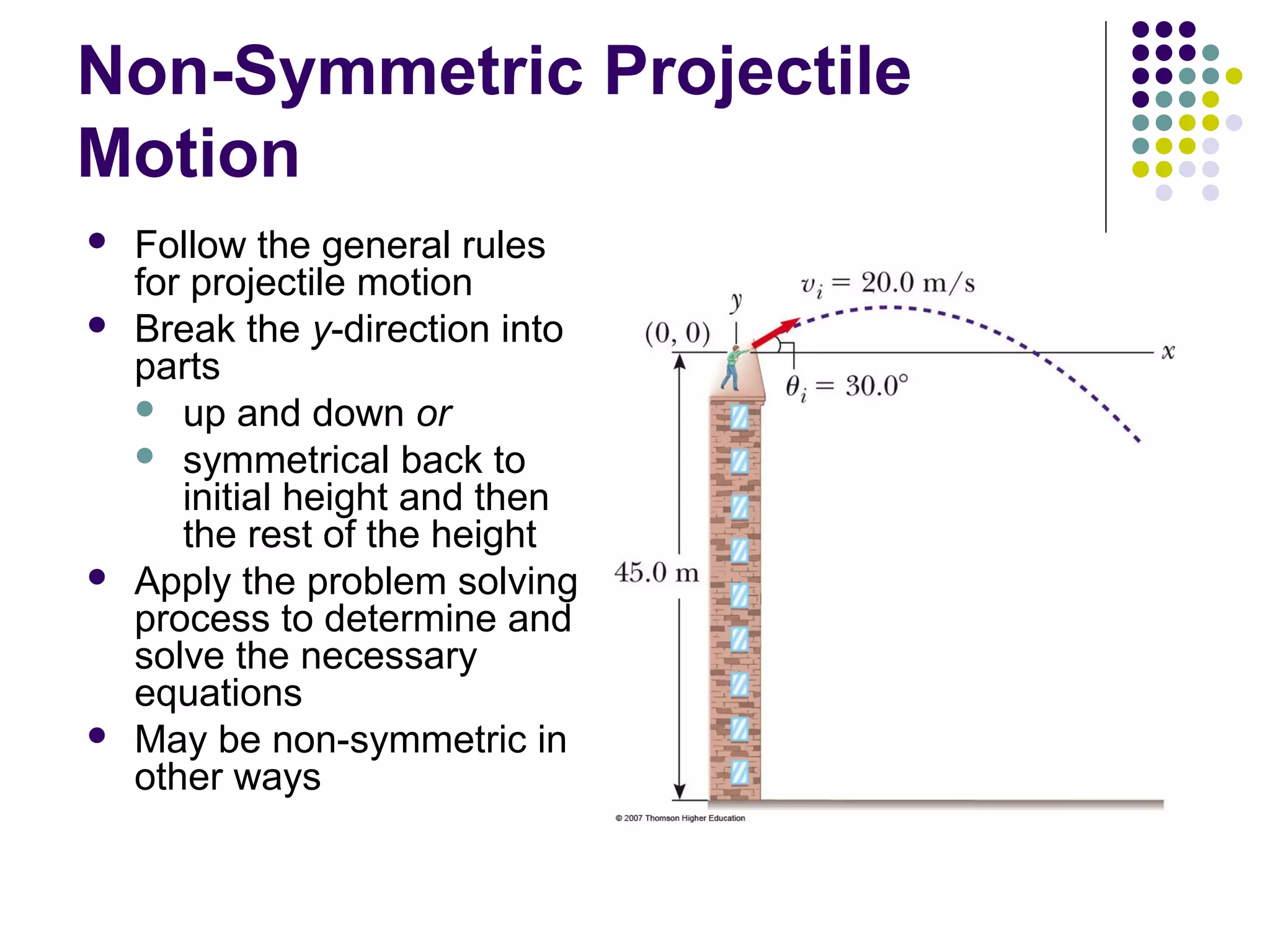
2) Projectile motion follows a parabolic path under constant acceleration due to gravity. It can be analyzed by separating it into horizontal and vertical motions.
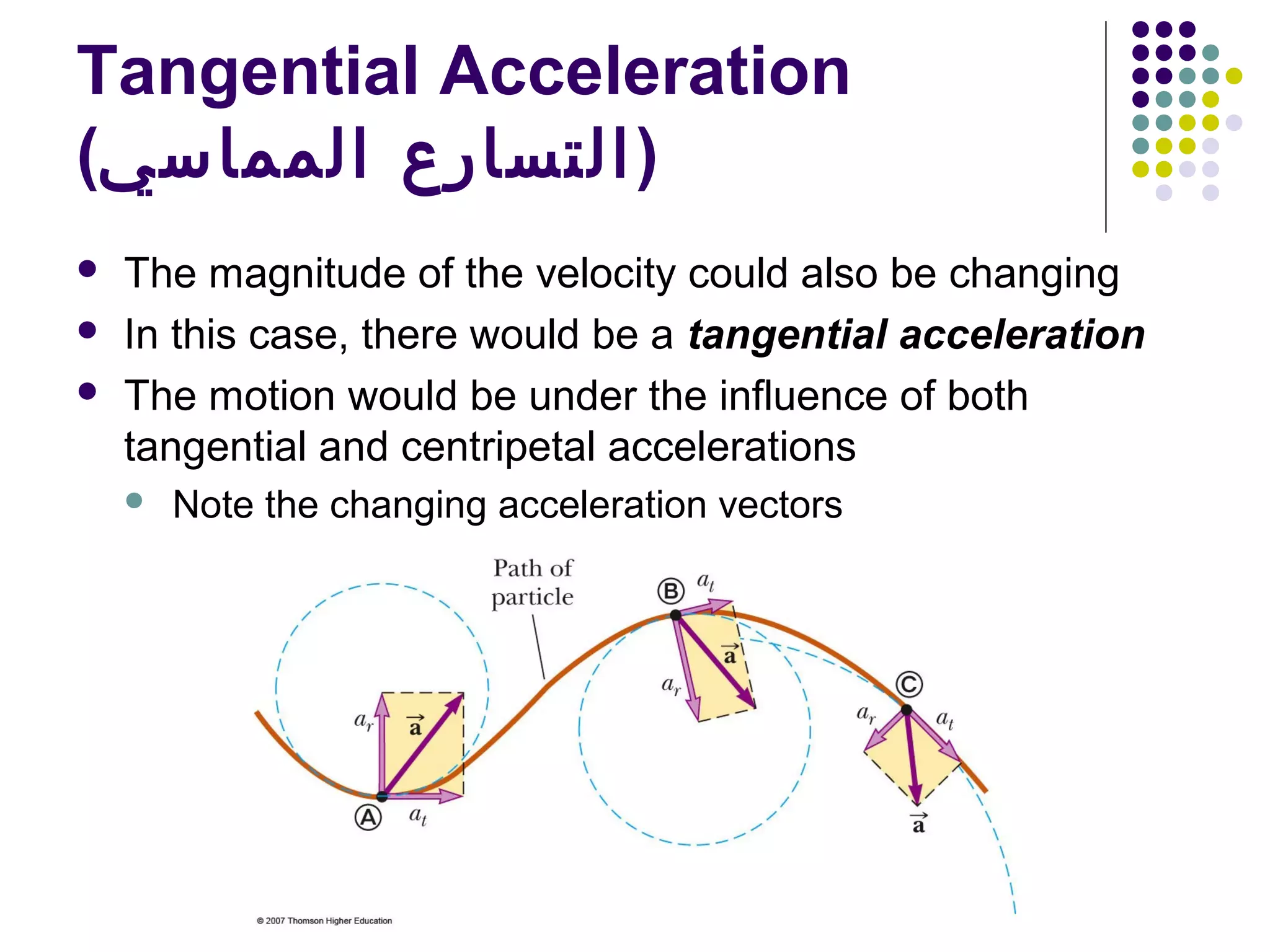
3) Uniform circular motion involves a constant speed but a changing velocity direction, producing a centripetal acceleration directed toward the center.