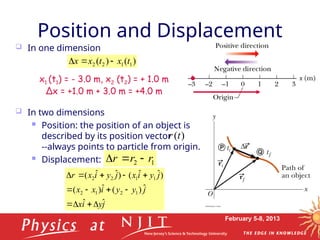
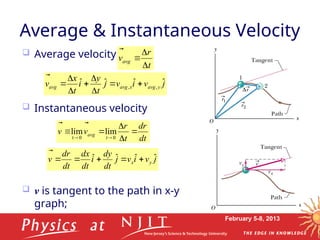
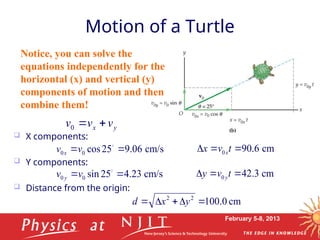
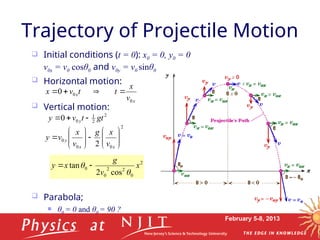
This document covers Lecture 3 of a physics course on mechanics, focusing on motion in two dimensions. Key topics include vectors, vector algebra, projectile motion, uniform circular motion, and relations of average and instantaneous velocity and acceleration. The lecture elaborates on kinematic variables and various equations governing motion in two-dimensional space.

1. Physics 111: Mechanics
Lecture 3
Dale Gary
NJIT Physics Department

2. February 5-8, 2013
Motion in Two Dimensions
 Reminder of vectors and vector algebra
 Displacement and position in 2-D
 Average and instantaneous velocity in 2-D
 Average and instantaneous acceleration in 2-
D
 Projectile motion
 Uniform circular motion
 Relative velocity*

3. February 5-8, 2013
Vector and its components
 The components are the
legs of the right triangle
whose hypotenuse is A
y
x A
A
A





2 2 1
tan y
x y
x
A
A A A and
A
   
    
 
)
sin(
)
cos(







A
A
A
A
y
x
Or,
   
 




















x
y
x
y
y
x
A
A
A
A
A
A
A
1
2
2
tan
or
tan 



4. February 5-8, 2013
 Which diagram can represent ?
A) B)
C) D)
Vector Algebra
1
2 r
r
r





r

2
r

1
r

r

2
r

1
r

r

2
r

1
r
 r

2
r

1
r

1
r



5. February 5-8, 2013
 Kinematic variables in one dimension
 Position: x(t) m
 Velocity: v(t) m/s
 Acceleration: a(t) m/s2
 Kinematic variables in three dimensions
 Position: m
 Velocity: m/s
 Acceleration: m/s2
 All are vectors: have direction and
magnitudes
Motion in two dimensions
k
v
j
v
i
v
t
v z
y
x
ˆ
ˆ
ˆ
)
( 



y
x
z
i
j
k
x
k
z
j
y
i
x
t
r ˆ
ˆ
ˆ
)
( 



k
a
j
a
i
a
t
a z
y
x
ˆ
ˆ
ˆ
)
( 




6. February 5-8, 2013
 In one dimension
 In two dimensions
 Position: the position of an object is
described by its position vector
--always points to particle from origin.
 Displacement:
x1 (t1) = - 3.0 m, x2 (t2) = + 1.0 m
Δx = +1.0 m + 3.0 m = +4.0 m
Position and Displacement
)
(t
r

1
2 r
r
r






j
y
i
x
j
y
y
i
x
x
j
y
i
x
j
y
i
x
r
ˆ
ˆ
ˆ
)
(
ˆ
)
(
)
ˆ
ˆ
(
)
ˆ
ˆ
(
1
2
1
2
1
1
2
2














)
(
)
( 1
1
2
2 t
x
t
x
x 


1
2 r
r
r







7. February 5-8, 2013
 Average velocity
 Instantaneous velocity
 v is tangent to the path in x-y
graph;
Average & Instantaneous Velocity
dt
r
d
t
r
v
v
t
avg










 0
0
t
lim
lim
j
v
i
v
j
t
y
i
t
x
v y
avg
x
avg
avg
ˆ
ˆ
ˆ
ˆ ,
, 








t
r
vavg





j
v
i
v
j
dt
dy
i
dt
dx
dt
r
d
v y
x
ˆ
ˆ
ˆ
ˆ 







8. February 5-8, 2013
Motion of a Turtle
A turtle starts at the origin and moves with the speed of v0=10 cm/s
in the direction of 25° to the horizontal.
(a) Find the coordinates of a turtle 10 seconds later.
(b) How far did the turtle walk in 10 seconds?

9. February 5-8, 2013
Motion of a Turtle
Notice, you can solve the
equations independently for the
horizontal (x) and vertical (y)
components of motion and then
combine them!
y
x v
v
v





0
0 0 cos25 9.06 cm/s
x
v v
 

 X components:
 Y components:
 Distance from the origin:
0 90.6 cm
x
x v t
  
0 0 sin 25 4.23 cm/s
y
v v
 

0 42.3 cm
y
y v t
  
cm
0
.
100
2
2




 y
x
d

10. February 5-8, 2013
 Average acceleration
 Instantaneous acceleration
 The magnitude of the velocity (the speed) can change
 The direction of the velocity can change, even though the
magnitude is constant
 Both the magnitude and the direction can change
Average & Instantaneous
Acceleration
dt
v
d
t
v
a
a
t
avg










 0
0
t
lim
lim
j
a
i
a
j
t
v
i
t
v
a y
avg
x
avg
y
x
avg
ˆ
ˆ
ˆ
ˆ ,
, 








t
v
aavg





j
a
i
a
j
dt
dv
i
dt
dv
dt
v
d
a y
x
y
x ˆ
ˆ
ˆ
ˆ 







11. February 5-8, 2013
 Position
 Average velocity
 Instantaneous velocity
 Acceleration
 are not necessarily same direction.
Summary in two dimension
j
y
i
x
t
r ˆ
ˆ
)
( 


j
a
i
a
j
dt
dv
i
dt
dv
dt
v
d
t
v
t
a y
x
y
x
t
ˆ
ˆ
ˆ
ˆ
lim
)
(
0












j
v
i
v
j
t
y
i
t
x
t
r
v y
avg
x
avg
avg
ˆ
ˆ
ˆ
ˆ ,
, 












j
v
i
v
j
dt
dy
i
dt
dx
dt
r
d
t
r
t
v y
x
t
ˆ
ˆ
ˆ
ˆ
lim
)
(
0












dt
dx
vx 
dt
dy
vy 
2
2
dt
x
d
dt
dv
a x
x 
 2
2
dt
y
d
dt
dv
a
y
y 

)
(
and
),
(
, t
a
t
v
(t)
r




12. February 5-8, 2013
Motion in two dimensions
t
a
v
v




 0
 Motions in each dimension are independent components
 Constant acceleration equations
 Constant acceleration equations hold in each dimension
 t = 0 beginning of the process;
 where ax and ay are constant;
 Initial velocity initial displacement ;
2
2
1
0 t
a
t
v
r
r







t
a
v
v y
y
y 
 0
2
2
1
0
0 t
a
t
v
y
y y
y 


)
(
2 0
2
0
2
y
y
a
v
v y
y
y 


t
a
v
v x
x
x 
 0
2
2
1
0
0 t
a
t
v
x
x x
x 


)
(
2 0
2
0
2
x
x
a
v
v x
x
x 


j
a
i
a
a y
x
ˆ
ˆ 


j
v
i
v
v y
x
ˆ
ˆ 0
0
0 


j
y
i
x
r ˆ
ˆ 0
0
0 



13. February 5-8, 2013
 Define coordinate system. Make sketch showing axes,
origin.
 List known quantities. Find v0x , v0y , ax , ay , etc. Show initial
conditions on sketch.
 List equations of motion to see which ones to use.
 Time t is the same for x and y directions.
x0 = x(t = 0), y0 = y(t = 0), v0x = vx(t = 0), v0y = vy(t = 0).
 Have an axis point along the direction of a if it is
constant.
Hints for solving problems
t
a
v
v y
y
y 
 0
2
2
1
0
0 t
a
t
v
y
y y
y 


)
(
2 0
2
0
2
y
y
a
v
v y
y
y 


t
a
v
v x
x
x 
 0
2
2
1
0
0 t
a
t
v
x
x x
x 


)
(
2 0
2
0
2
x
x
a
v
v x
x
x 



14. February 5-8, 2013
 2-D problem and define a coordinate
system: x- horizontal, y- vertical (up +)
 Try to pick x0 = 0, y0 = 0 at t = 0
 Horizontal motion + Vertical motion
 Horizontal: ax = 0 , constant velocity
motion
 Vertical: ay = -g = -9.8 m/s2
, v0y = 0
 Equations:
Projectile Motion
2
2
1
gt
t
v
y
y iy
i
f 


t
a
v
v y
y
y 
 0
2
2
1
0
0 t
a
t
v
y
y y
y 


)
(
2 0
2
0
2
y
y
a
v
v y
y
y 


t
a
v
v x
x
x 
 0
2
2
1
0
0 t
a
t
v
x
x x
x 


)
(
2 0
2
0
2
x
x
a
v
v x
x
x 


Horizontal Vertical

15. February 5-8, 2013
 X and Y motions happen independently,
so we can treat them separately
 Try to pick x0 = 0, y0 = 0 at t = 0
 Horizontal motion + Vertical motion
 Horizontal: ax = 0 , constant velocity
motion
 Vertical: ay = -g = -9.8 m/s2
 x and y are connected by time t
 y(x) is a parabola
Projectile Motion
gt
v
v y
y 
 0
2
2
1
0
0 gt
t
v
y
y y 


x
x v
v 0

t
v
x
x x
0
0 

Horizontal Vertical

16. February 5-8, 2013
 2-D problem and define a coordinate
system.
 Horizontal: ax = 0 and vertical: ay = -g.
 Try to pick x0 = 0, y0 = 0 at t = 0.
 Velocity initial conditions:
 v0 can have x, y components.
 v0x is constant usually.
 v0y changes continuously.
 Equations:
Projectile Motion
0
0
0 cos
v
v x 
Horizontal
Vertical
0
0
0 sin
v
v x 
gt
v
v y
y 
 0
2
2
1
0
0 gt
t
v
y
y y 


x
x v
v 0

t
v
x
x x
0
0 


17. February 5-8, 2013
 Initial conditions (t = 0): x0 = 0, y0 = 0
v0x = v0 cosθ0 and v0y = v0 sinθ0
 Horizontal motion:
 Vertical motion:
 Parabola;
 θ0 = 0 and θ0 = 90 ?
Trajectory of Projectile Motion
2
2
1
0
0 gt
t
v
y y 


x
x
v
x
t
t
v
x
0
0
0 



2
0
0
0
2 

















x
x
y
v
x
g
v
x
v
y
2
0
2
2
0
0
cos
2
tan x
v
g
x
y

 


18. February 5-8, 2013
 Initial conditions (t = 0): x0 = 0, y0 = 0
v0x = v0 cosθ0 and v0x = v0 sinθ0, then
What is R and h ?
Horizontal Vertical
2
2
1
0
0
0 gt
t
v y 


t
v
x x
0
0 

g
v
g
v
v
t
v
x
x
R x
0
2
0
0
0
0
0
0
0
2
sin
sin
cos
2 







g
v
g
v
t y 0
0
0 sin
2
2 


2
0
2
2
1
0
0
2
2
2












t
g
t
v
gt
t
v
y
y
h y
h
h
y
g
v
h
2
sin 0
2
2
0 

y
y
y
y
y v
g
v
g
v
gt
v
v 0
0
0
0
2






h
gt
v
v y
y 
 0
2
2
1
0
0 gt
t
v
y
y y 


x
x v
v 0

t
v
x
x x
0
0 


19. February 5-8, 2013
Projectile Motion
at Various Initial Angles
 Complementary
values of the initial
angle result in the
same range
 The heights will be
different
 The maximum range
occurs at a
projection angle of
45o
g
v
R

2
sin
2
0


20. February 5-8, 2013
Uniform circular motion
Constant speed, or,
constant magnitude of velocity
Motion along a circle:
Changing direction of velocity

21. February 5-8, 2013
Circular Motion: Observations
 Object moving along a
curved path with constant
speed
 Magnitude of velocity: same
 Direction of velocity:
changing
 Velocity: changing
 Acceleration is NOT zero!
 Net force acting on the
object is NOT zero
 “Centripetal force”
a
m
Fnet




22. February 5-8, 2013
 Centripetal acceleration
 Direction: Centripetal
Uniform Circular Motion
r
v
t
v
a
r
v
r
v
t
r
t
v
r
r
v
v
r
r
v
v
r
2
2
so,
















O
x
y
ri
R
A B
vi
rf
vf
Δr
vi
vf
Δv = vf - vi

23. February 5-8, 2013
Uniform Circular Motion
 Velocity:
 Magnitude: constant v
 The direction of the velocity is
tangent to the circle
 Acceleration:
 Magnitude:
 directed toward the center of
the circle of motion
 Period:
 time interval required for one
complete revolution of the
particle
r
v
ac
2

r
v
ac
2

v
r
T

2

v
ac




24. February 5-8, 2013
 Position
 Average velocity
 Instantaneous velocity
 Acceleration
 are not necessarily in the same direction.
Summary
j
y
i
x
t
r ˆ
ˆ
)
( 


j
a
i
a
j
dt
dv
i
dt
dv
dt
v
d
t
v
t
a y
x
y
x
t
ˆ
ˆ
ˆ
ˆ
lim
)
(
0












j
v
i
v
j
t
y
i
t
x
t
r
v y
avg
x
avg
avg
ˆ
ˆ
ˆ
ˆ ,
, 












j
v
i
v
j
dt
dy
i
dt
dx
dt
r
d
t
r
t
v y
x
t
ˆ
ˆ
ˆ
ˆ
lim
)
(
0












dt
dx
vx 
dt
dy
vy 
2
2
dt
x
d
dt
dv
a x
x 
 2
2
dt
y
d
dt
dv
a
y
y 

)
(
and
),
(
, t
a
t
v
(t)
r




25. February 5-8, 2013
 If a particle moves with constant acceleration a, motion
equations are
 Projectile motion is one type of 2-D motion under constant
acceleration, where ax = 0, ay = -g.
Summary
j
t
a
t
v
y
i
t
a
t
v
x
j
y
i
x
r yi
yi
i
xi
xi
i
f
f
f
ˆ
)
(
ˆ
)
(
ˆ
ˆ 2
2
1
2
2
1









j
t
a
v
i
t
a
v
j
v
i
v
t
v y
iy
x
ix
fy
fx
f
ˆ
)
(
ˆ
)
(
ˆ
ˆ
)
( 






t
a
v
v i





2
2
1
t
a
t
v
r
r i
i
f






