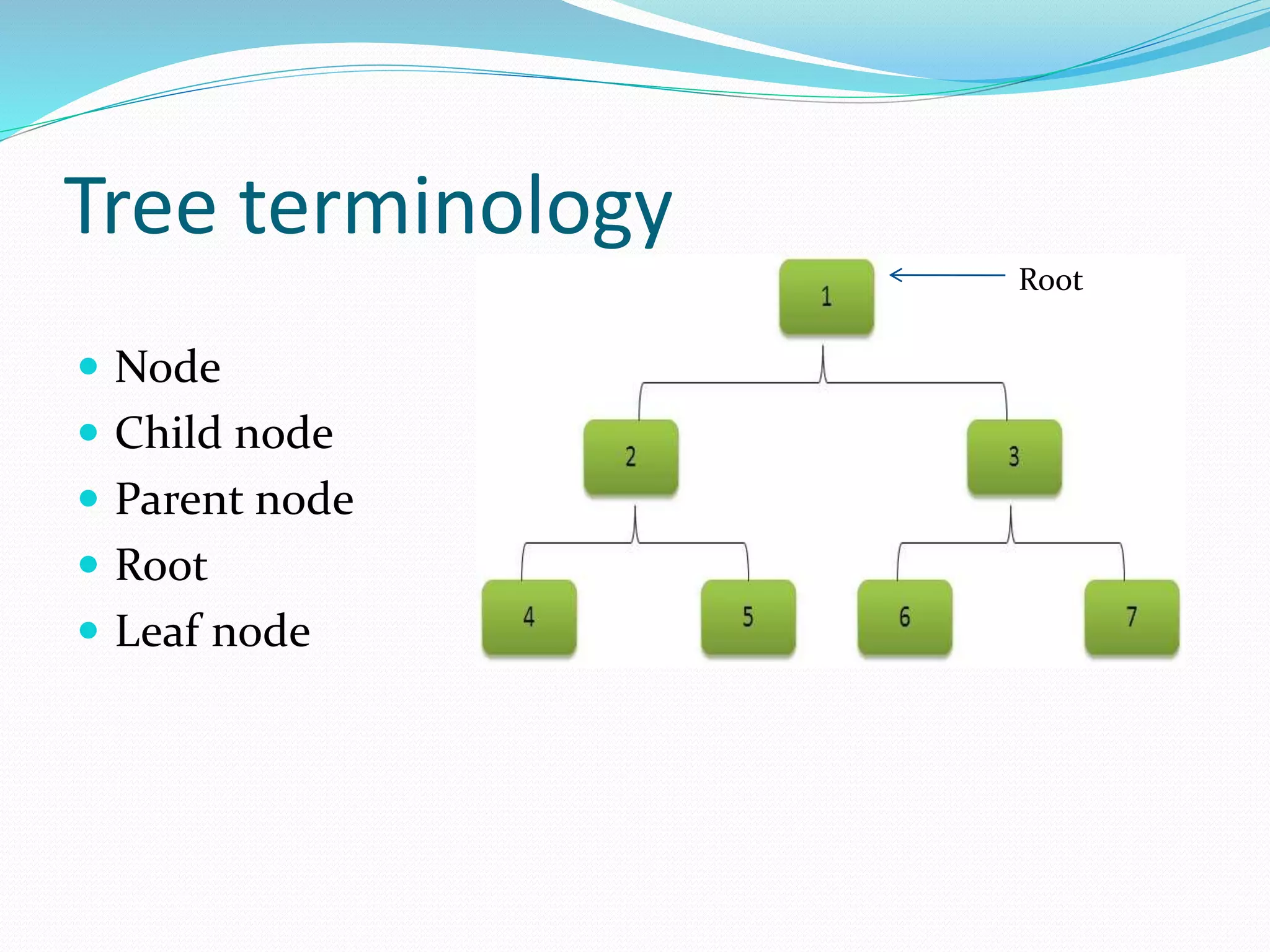
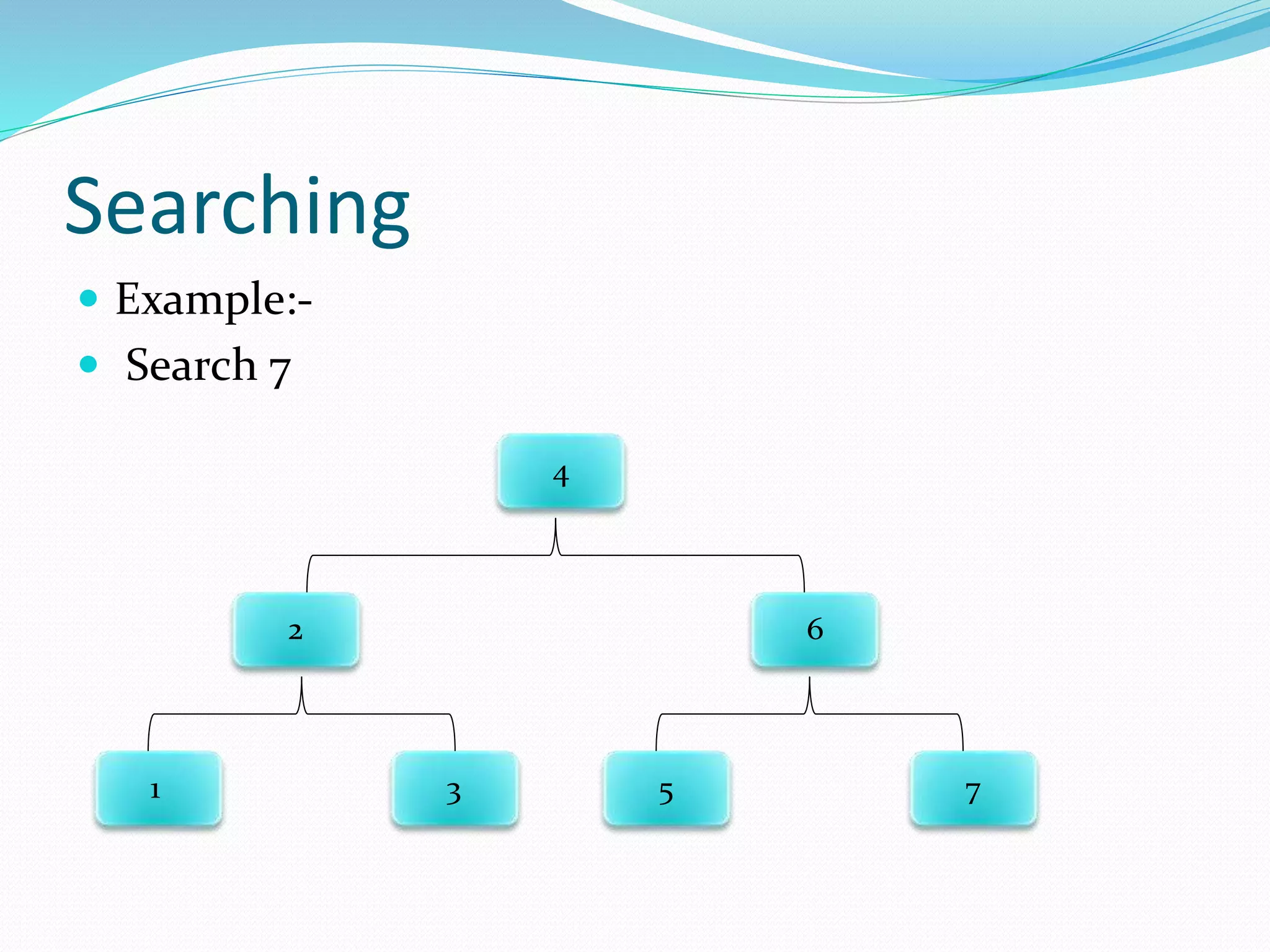
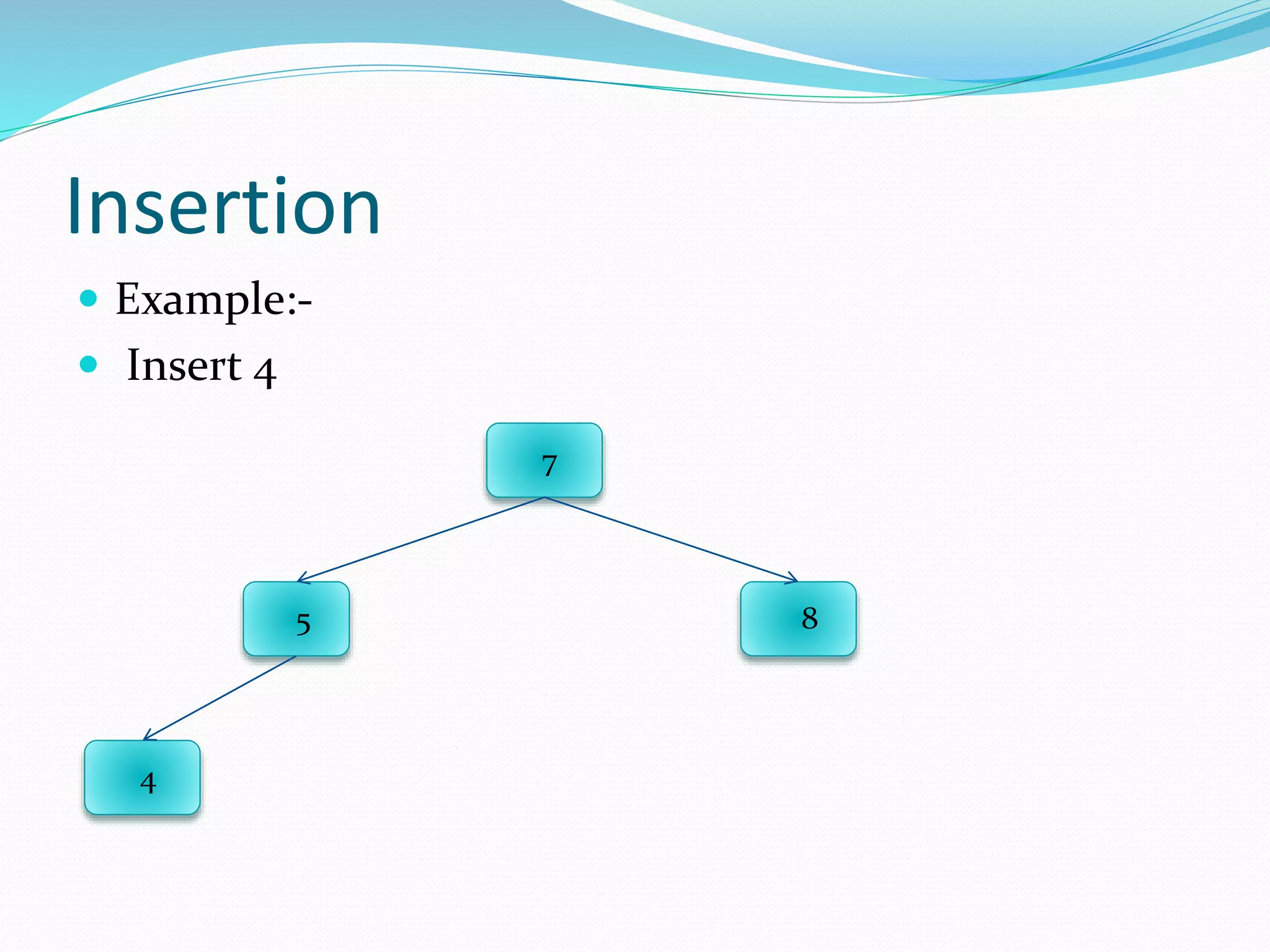
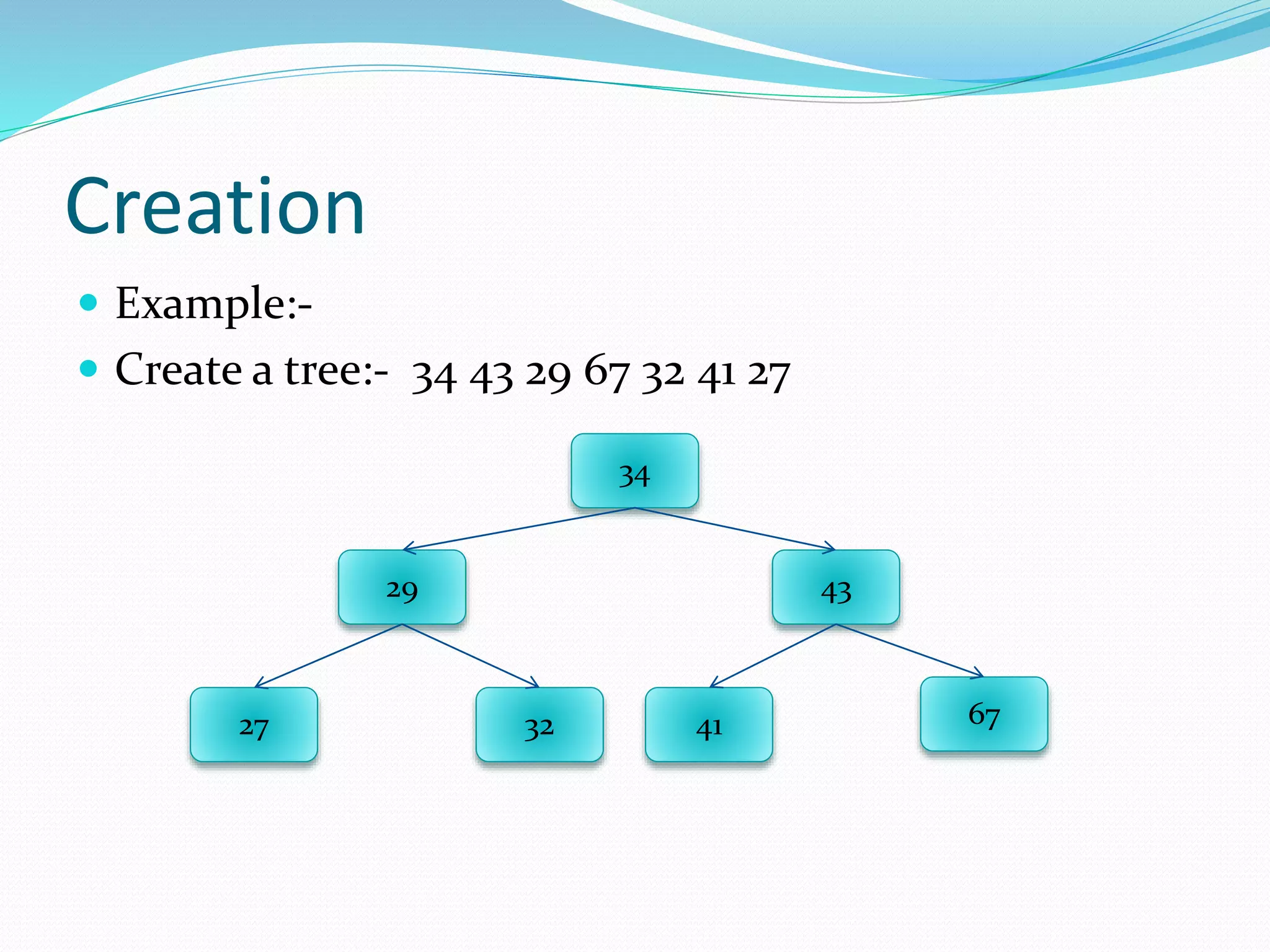
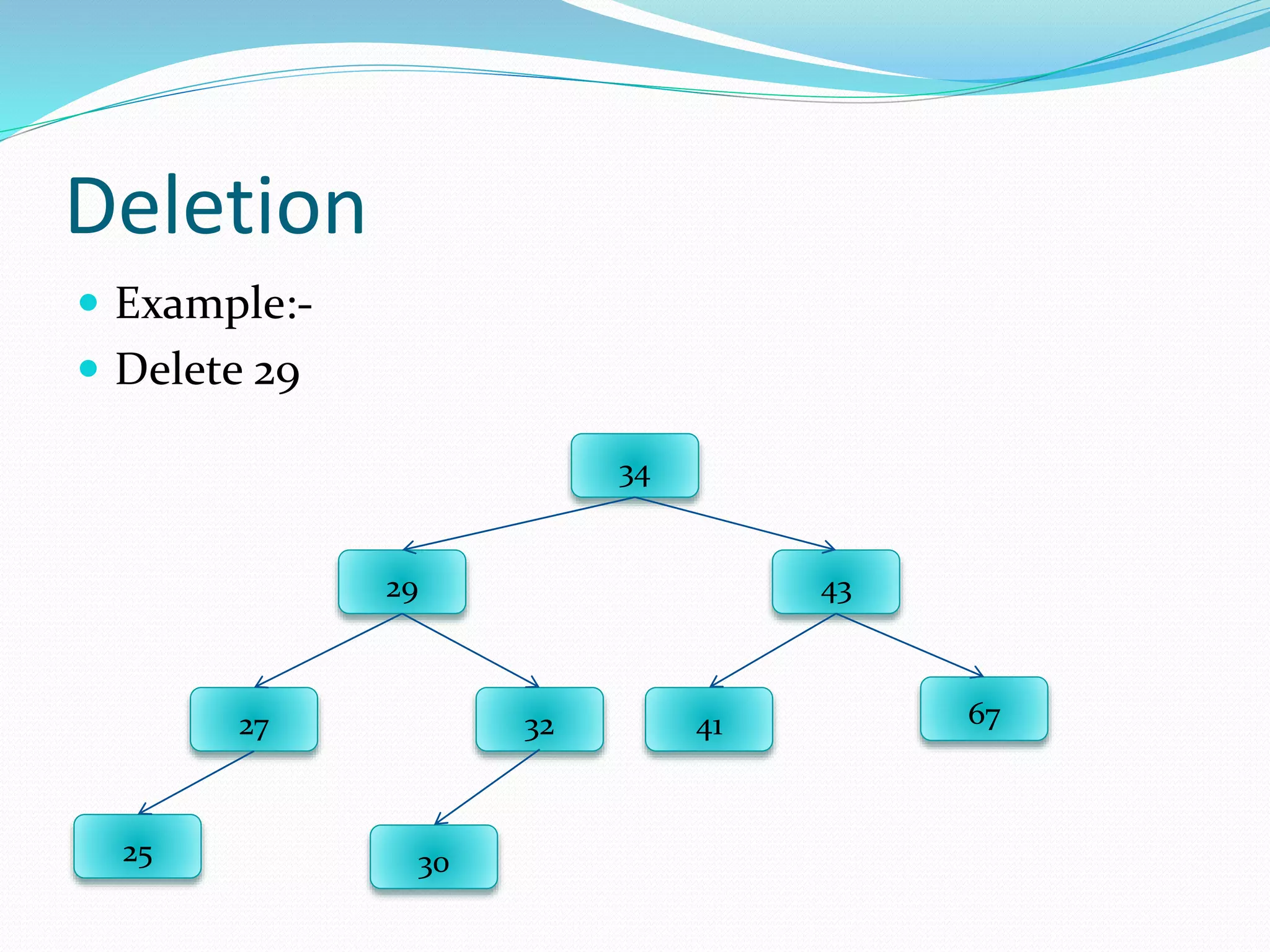
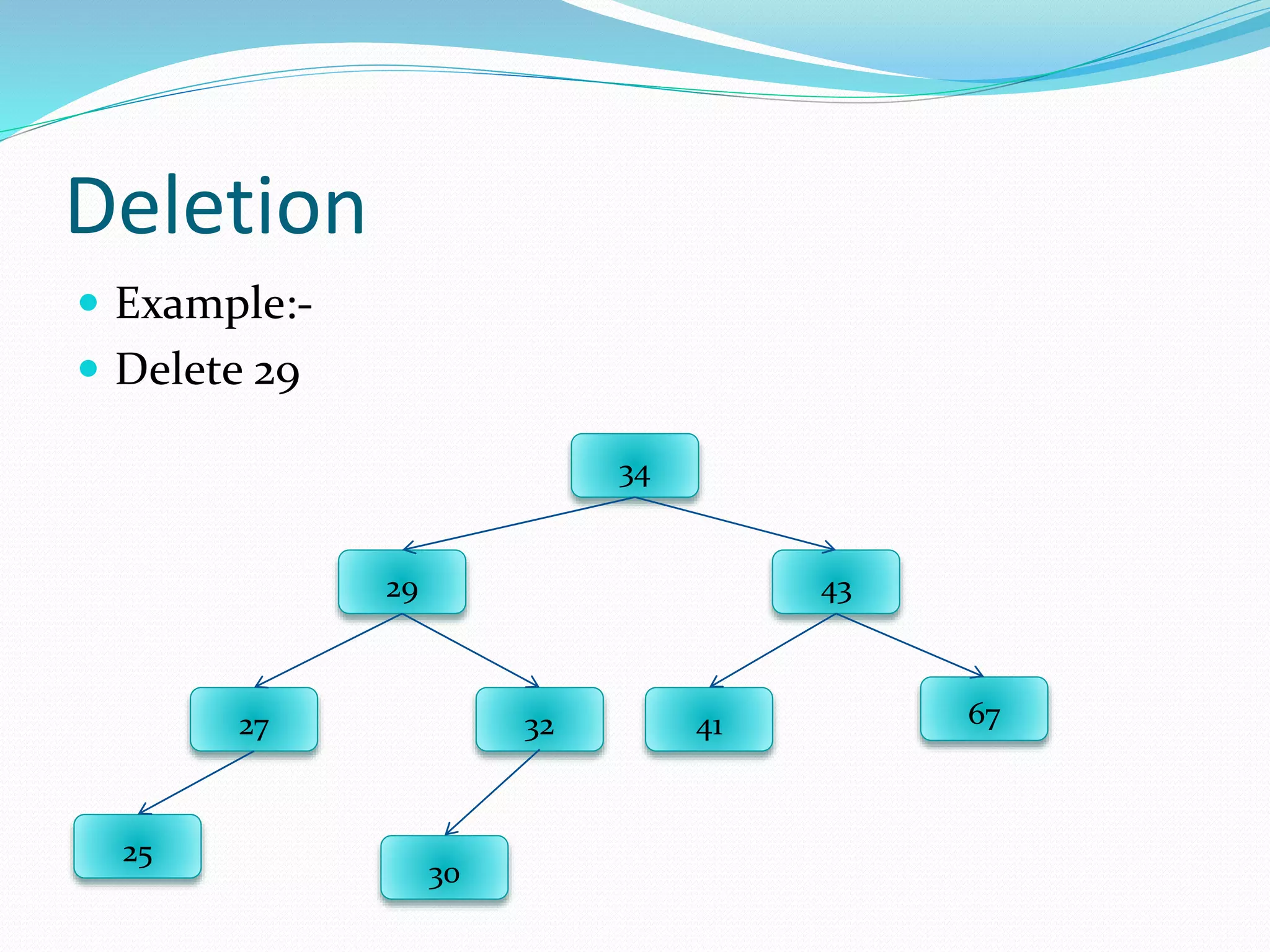
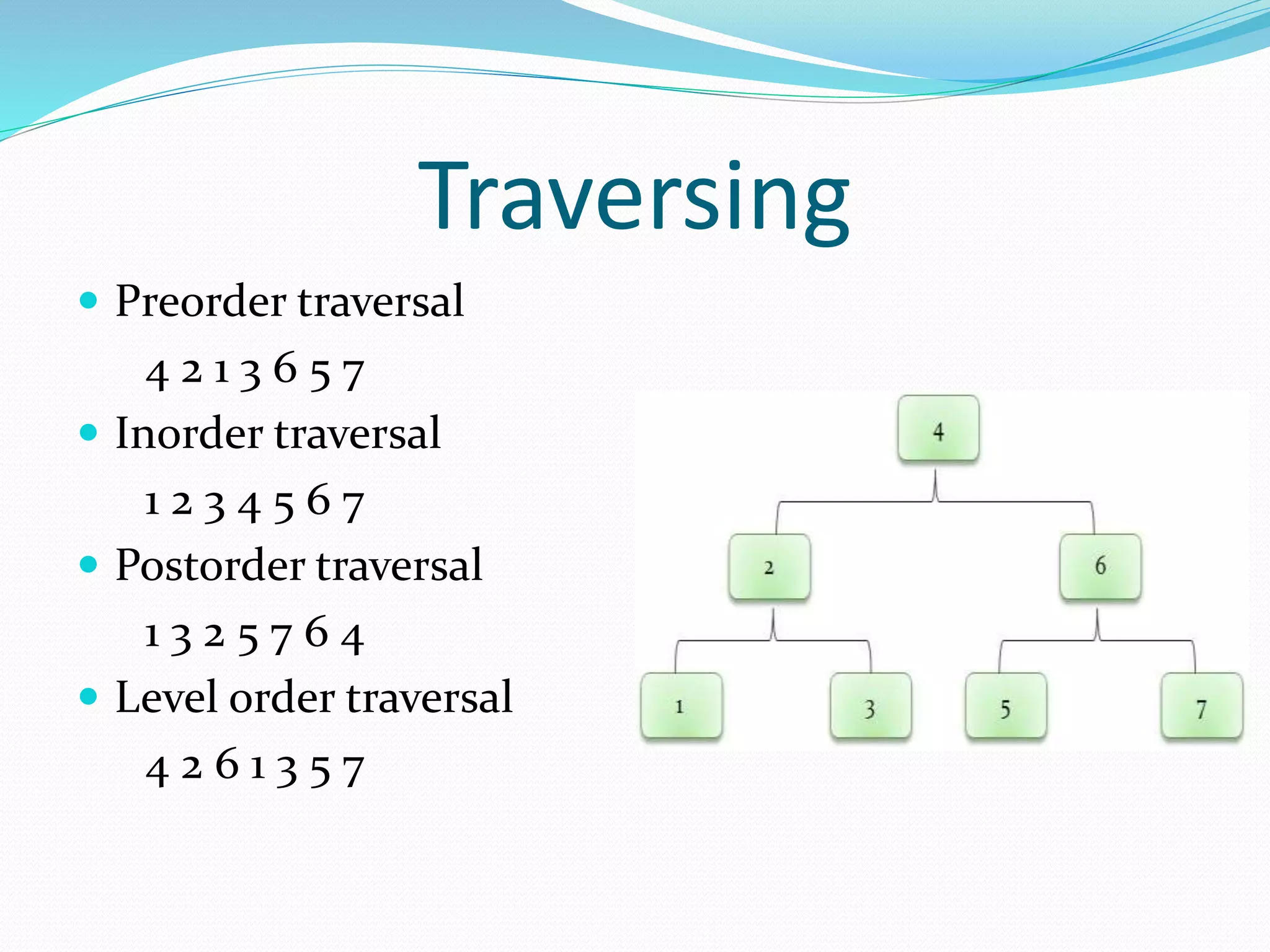
The document discusses binary trees, including their terminology, implementation, operations, and traversal methods. It lists the group members and then defines key binary tree concepts like nodes, children, parents, roots, and leaf nodes. It explains that a binary tree has at most two children per node, and describes how to implement one using linked lists. Common binary tree operations like searching, insertion, deletion, creation, and traversing are then covered with examples. The different traversal orders - preorder, inorder, postorder, and level order - are defined along with examples.

3. Group members
 M. Waheed Khalid 12-cse-43
 Syed Faisal Sabbir 12-cse-59
 Saqlain Hussain Shah 12-cse-69
 Saddaqat hussain 12-cse-44

4. Trees
 Non linear data structure.
 Hierarchical structure consist of nodes.
 Used to represent data contain hierarchical
relationship.

5. Tree terminology
 Node
 Child node
 Parent node
 Root
 Leaf node
Root

6. Binary tree
 Every node has at most two children.
 Either empty or partitioned into three disjoint subsets.
 First is root.
 Other two are left and right subtree and satisfies
following conditions:-
 All keys of left subtree of root are less than the key of root
 All keys of right subtree of root are greater than the key of
root
 Left and right subtree of root are also binary trees

7. Implementation
 Binary tree can be implemented by using linked list
 Each node will consist
 Value stored in node
 Pointer to the next node at the right
 Pointer to the next node at the left

8. Operation on binary tree
 Searching
 Insertion
 Creation
 Deletion
 Traversing

9. Searching
 Start from the root node and move down in tree by
comparing the desired key with key of node
 If the desired key is equal to key in node then search is
successful and take appropriate action
 If desired key is less than key of node then move to left child.
 If desired key is greater than key of node then move to right
child.
 If we reach NULL then search is unsuccessful i.e. desired key is
not present..

10. Searching
 Example:-
 Search 7
4
2 6
1 3 5 7

11. Insertion
 Insertion a node consisting of two operations:-
 First, the tree must be searched where the node is inserted
 Second, the node is inserted into the tree on completion
 Insert into an Empty tree:-
 In this case, node is inserted into tree considered as root
 Insert into a non-Empty tree:-
 In this case, tree is searched and then insert node in the tree

12. Insertion
 Example:-
 Insert 4
7
85
4

13. Creation
 Binary tree is created by repeating insertion of nodes
but insertion must maintain the order of tree. e.g.
 First ,root is insert then next node.
 If the value of new node is less than root then appended
it as left leaf of node.
 If the value of new node is greater than root then
appended it as right leaf of node.

14. Creation
 Example:-
 Create a tree:- 34 43 29 67 32 41 27
34
29
6732
43
4127

15. Deletion
 Deletion consist of two operations, searching and
deletion. We can delete following nodes node:-
 Node has no children
 Node has one children
 Node has two children
 Replace node with it’s the inorder successor node
 Else if no right subtree exists replace with it’s left child

16. Deletion
 Example:-
 Delete 29
34
29
6732
43
4127
3025

17. Deletion
 Example:-
 Delete 29
34
29
6732
43
4127
30
25

18. Traversing in binary tree
 Preorder traversal (NLR)
 Inorder traversal (LNR)
 Postorder traversal (LNR)
 Level order traversal

19. Traversing
 Preorder traversal
4 2 1 3 6 5 7
 Inorder traversal
1 2 3 4 5 6 7
 Postorder traversal
1 3 2 5 7 6 4
 Level order traversal
4 2 6 1 3 5 7

20. Any question?