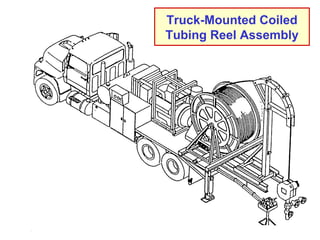
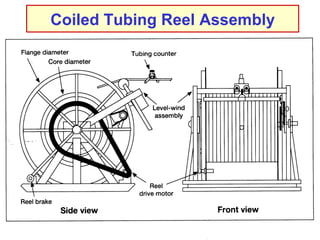
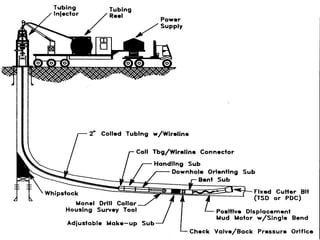
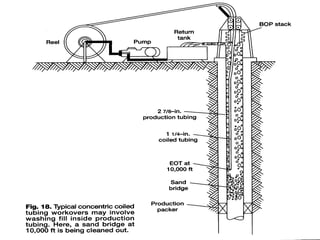
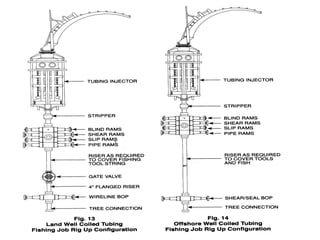
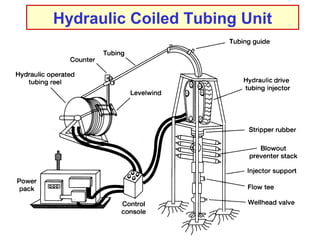
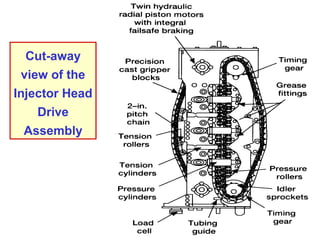
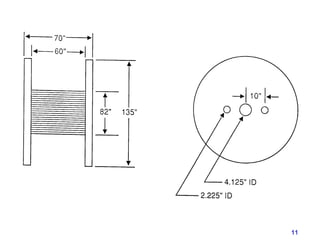
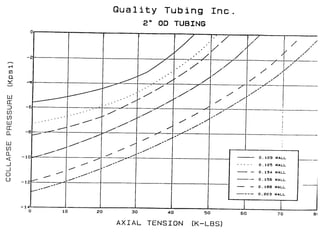
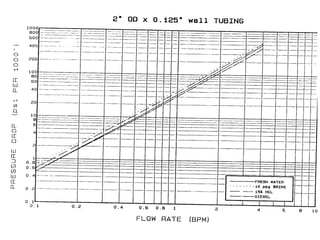
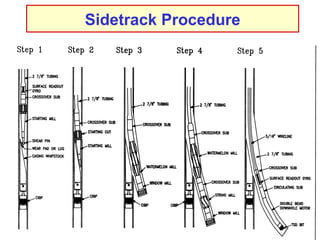
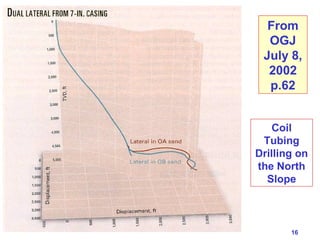
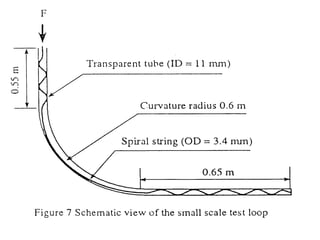
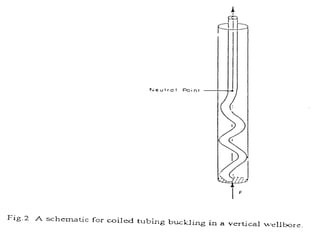
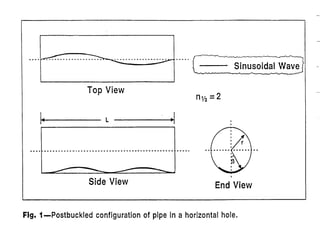
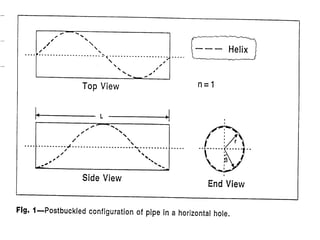
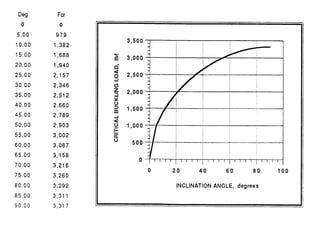
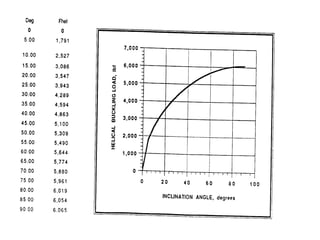
The document discusses buckling of coiled tubing in different wellbore orientations. It defines several buckling modes including sinusoidal, helical, and buckling in vertical or horizontal sections. Equations are provided to calculate the critical buckling loads for these different modes based on the tubing's material properties and dimensions. Examples are shown for a 2" diameter coiled tubing string. Buckling loads are lowest in the horizontal orientation and highest in vertical wells due to additional support from tubing weight.

1. 1
PETE 411
Well Drilling
Lesson 37
Coiled Tubing

2. 2
Coiled Tubing
 What is Coiled Tubing?
 Uses of Coiled Tubing
 Properties of Coiled Tubing
 Drilling with Coiled Tubing
 Buckling

3. 3
Buckling of Coiled Tubing
 Buckling Modes
 Sinusoidal and Helical Buckling
 Buckling in Horizontal or Inclined Sections
 Buckling in Vertical Section
 Buckling in Curved Wellbores
 Prediction of Buckling Loads
 “Lockup” of Tubulars

4. Truck-Mounted Coiled
Tubing Reel Assembly
4

5. 5
Coiled Tubing Reel Assembly

6. 6

7. 7

8. 8

9. 9
Hydraulic Coiled Tubing Unit

10. 10
Cut-away
view of the
Injector Head
Drive
Assembly

11. 11

12. 12

13. 13

14. Some Applications of Coiled Tubing
• Cementing
• Plug Cementing (e.g. P&A)
• Squeeze Cementing
• Logging
• Drilling
• Producing
• Fishing
• Scale Removal
Ref: SPE Reprint Series NO. 38 “Coiled Tubing Technology”
14

15. 15
Sidetrack Procedure

16. From
OGJ
July 8,
2002
p.62
Coil
Tubing
Drilling on
the North
Slope
16

17. 17
Coil Tubing Drilling on the North Slope
 Drilling Rates routinely in excess of
250 ft/hr - drilling in sandstone
 Laterals longer than 2,500 ft
 Good incremental oil production
 Used electrical umbilical for MWD
 Used mud motors and 3 ¾-in PDC bits

18. 18
Advantages
 No rig required
 No connections - fast tripping
Disadvantages
 Fatigue life limit (cycles)
 Pressure and tension
 Diameter and ovality

19. 19
Reference:
“Coiled Tubing Buckling Implication in
Drilling and Completing Horizontal Wells”
by Jiang Wu and H.C. Juvkam-Wold, SPE
Drilling and Completion, March, 1995.

20. 20

21. 21

22. 22

23. 23

24. Sinusoidal Buckling in a Horizontal Wellbore
When the axial compressive load along the coiled
tubing reaches the following sinusoidal buckling
load Fcr, the intial (sinusoidal or critical) buckling
of the coiled tube will occur in the horizontal
wellbore.
24
2 0.5
cr e F = (EIW / r)
r

25. 25
Consider:
= p - =
(2 1.688 )12*65.45
4
2.67 lb
W 3.07 1 8.6
ö çè= - æ -
E 30,000,000 psi (steel)
3.07 lb
0.2225 lb
ft
ft
65.45
ft
231
W
gal mud
2" OD, 1.688" ID; 8.6 #
e
2 2
=
= = ÷ø
in
*
2 0.5
Fcr = (EIWe / r)

26. F E IWe
cr = 2
3.317 lbf
26
= p - = p - =
= - = 3.875 - 2
-
r D HOLE
OD
Then, F 2 30*10 *0.3869*0.2225
0.9375
0.9375 in
2
2
(2 1.688 ) 0.3869 in
64
(OD ID )
64
I
6 0.5
cr
4 4 4 4 4
ö
= ÷ ÷ø
ç çè æ
=
Consider:
,
=
r

27. 27
Sinusoidal Buckling Load
A more general Sinusoidal Buckling Load
equation for highly inclined wellbores (including
the horizontal wellbore) is:
F EIWe sin
cr
= 2 q
r q

28. 28
Sinusoidal Buckling Load
For the same 2” OD coiled tubing, at q = 45o
F EIWe sin
cr
= 2 q
r
6 0 5
F * * . * . sin ÷ ÷ø
2 30 10 0 3869 0 2225 45
0 9375
o .
cr .
ö
ç çè æ
=
Fcr = 2,789 lbf

29. 29

30. Helical Buckling in a Horizontal Wellbore
When the axial compressive load reaches the
following helical buckling load Fhel in the horizontal
wellbore, the helical buckling of coiled tubing then
occurs: ( ) r
30
F E IWe
hel = 2 2 2 -1
( ) 0 9375
6
F = -
* * . * . hel 2 2 2 1 30 10 0 3869 0 2225
.
Fhel = 6,065 lbf

31. 31
General Equation
A more general helical buckling load
equation for highly inclined wellbores
(including the horizontal wellbore) is:
( ) r
F EIWe sin
hel
= 2 2 2 -1 q

32. 32

33. 33
Buckling in Vertical Wellbores:
In a vertical wellbore, the buckling of coiled tubing
will occur if the coiled tubing becomes axially
compressed and the axial compressive load
exceeds the buckling load in the vertical section.
This could happen when we “slack-off” weight at
the surface to apply bit weight for drilling and
pushing the coiled tubing through the build section
and into the horizontal section.

34. 34
Buckling in Vertical Wellbores:
Lubinski derived in the 1950’s the following
buckling load equation for the initial buckling
of tubulars in vertical wellbores:
=
F 1.94(EIW )
=
F 1.94(30*10 *0.3869*0.2225 )
F 161 lbf
cr,b
6 2 1/3
cr,b
2 1/3
cr,b e
=

35. 35
Buckling in Vertical Wellbores:
Another intitial buckling load equation for
tubulars in vertical wellbores was also
derived recently through an energy analysis:
=
F 2.55(EIW )
F 2.55(30*10 *0.3869*0.2225 )
Alternate F 212 lbf (Table 1)
cr,b
6 2 1/3
cr,b
2 1/3
cr,b e
=
=

36. 36
Helical Buckling in Vertical Wellbores:
A helical buckling load for weighty tubulars in
vertical wellbores was also derived recently through
an energy analysis to predict the occurrence of the
helical buckling:
F 5.55(EIW 2 )1/3
hel,b e
461 lbf
=
=

37. Helical Buckling in Vertical Wellbores:
37
This helical buckling load predicts the first
occurrence of helical buckling of the weighty
tubulars in the vertical wellbore. The first
occurrence of helical buckling in the vertical
wellbore will be a one-pitch helical buckle at
the bottom portion of the tubular.

38. Helical Buckling in Vertical Wellbores:
The upper portion of the tubular in the vertical
wellbore will be in tension and remain straight.
When more tubular weight is slacked-off at the
surface, and the helical buckling becomes more
than one helical pitch, the above helical buckling
load equation may be used for the top helical
pitch of the helically buckled tubular
38

39. 39
Helical Buckling in Vertical Wellbores:
The top helical buckling load Fhel,t is calculated by
simply subtracting the tubular weight of the initial
one-pitch of helically buckled pipe from the
helical buckling load Fhel,b, which is defined at the
bottom of the one-pitch helically buckled tubular:
= -
F 5.55(EIW ) W L
2 1/3
e
e hel
2 1/3
hel,t e
0.14(EIW )
=

40. Helical Buckling in Vertical Wellbores:
40
Where the length of the initial one-pitch of
helical buckling or the first order helical
buckling is:
L (16 EI /W )1/3 (10)
e
2
hel = p

41. Helical Buckling in Vertical Wellbores:
From Table 1, it is also amazing to find out that
the top helical buckling load, Fhel,t, is very close to
zero. This indicates that the “neutral point”, which
is defined as the place of zero axial load (effective
axial load exclusive from the hydrostatic pressure
force), could be approximately used to define the
top of the helical buckling for these coiled tubings.
41

42. Helical Buckling in Vertical Wellbores:
42
2 1/3
=
F 0.14(EIW )
0.14(30*10 *0.3869*0.2225 )
=
F 12 lbf
hel,t
6 2 1/ 2
hel,t e
=

43. Sinusoidal: cr = 2 = 3,317 lbf
43
Buckling of 2” x 1.688” CT
Horizontal
F E IWe
r
hel ( ) cr F = 2 2 -1 F
Helical: = 6,065 lbf

44. 44
Buckling of 2” x 1.688” CT
Vertical
Sinusoidal, bottom:
or
F = 1 . 94 (E IW 2 ) 1 /
3 =
cr,b e 161 lbf F = 2 . 55 (E IW 2 ) 1 /
3 =
cr,b e 212 lbf

45. 45
Buckling of 2” x 1.688” CT
Vertical
Helical, bottom:
F . (E IW ) lbf /
Helical, top:
hel,b 5 55 e 461 2 1 3 = =
F = 0 . 14 (E IW 2 ) 1 /
3 =
hel,b e 12 lbf