This document discusses the universal approximation theorem for deep neural networks. It begins by motivating deep learning as a way to automatically learn complex decision boundaries without manual feature engineering. It then introduces the universal approximation theorem, which states that a multi-layer perceptron can represent any given function, allowing deep neural networks to theoretically learn anything given enough data. The document proceeds to provide mathematical definitions and proofs related to functional analysis, topology, and linear algebra in order to prove the universal approximation theorem. It concludes by stating the theorem can extend to any measurable activation function and probability measure.













![IDS Lab
Jamie Seol
Analysis 101
• Asequence {an} in metric space M is said to be a cauchy if for ∀ε > 0,
∃N s.t. for ∀n, m > N, d(an, am) < ε holds
• Ametric space M is said to be complete if every cauchy sequence
converges
• very, very typical complete space: ℝ
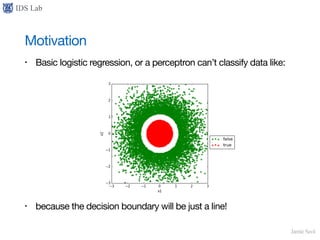
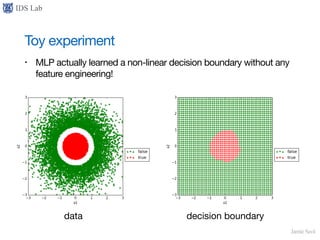
• but this is not trivial
• for example, rational sequence {an} satisfying an ∈ [π - 1/n, π + 1/n] is
cauchy, but it never converges!](https://image.slidesharecdn.com/universalapproximationtheorem-170112081014/85/Universal-Approximation-Theorem-18-320.jpg)

![IDS Lab
Jamie Seol
RealAnalysis 101
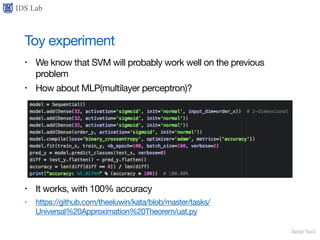
• We say a function is measurable if f−1(A) is measurable for any open set A
• maybe we should stop here…
• if someone meets non-measurable function by chance, it’ll be one of
the most unlucky day ever
• one old mathematician said, “If someone built an airplane using
non-measurable function, then I’ll not ride the plane”
• Anyway, a measure is something that measures area of a set
• for example, µ([a, b]) = b - a will hold as intuitively in ℝ with
Lebesgue measure µ
• we say some property p holds almost everywhere in A if the measure
of {x ∈ A | ¬p(x)} is 0
• note that the probability, is measure of an event!](https://image.slidesharecdn.com/universalapproximationtheorem-170112081014/85/Universal-Approximation-Theorem-20-320.jpg)


![IDS Lab
Jamie Seol
Notations
• Afunction 𝛹: ℝ → [0, 1] is a squashing function if
• non-decreasing
• limit to +∞ gives 1, -∞ gives 0
• examples: positive indicator function, standard sigmoid function
• Cr = set of continuous function from ℝr to ℝ
• if G is continuous, both ∑r(G) and ∑∏r(G) belongs to Cr
• Mr = set of measurable function from ℝr to ℝ
• if G is measurable, both ∑r(G) and ∑∏r(G) belongs to Mr
• note that Cr is subset of Mr](https://image.slidesharecdn.com/universalapproximationtheorem-170112081014/85/Universal-Approximation-Theorem-23-320.jpg)










