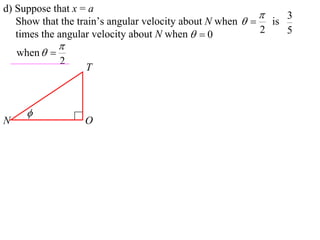
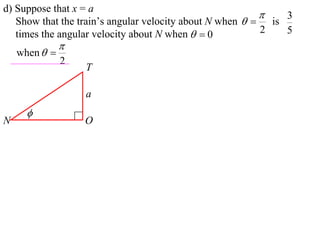
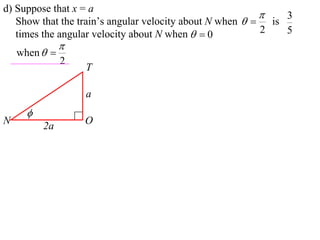
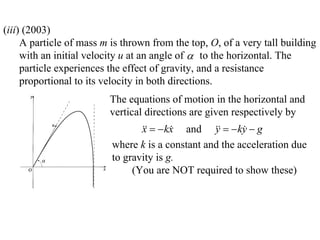
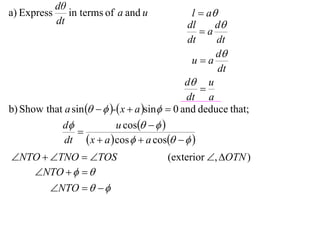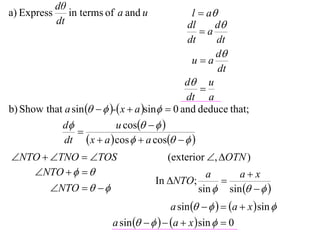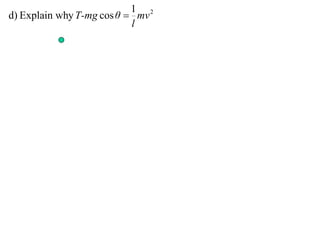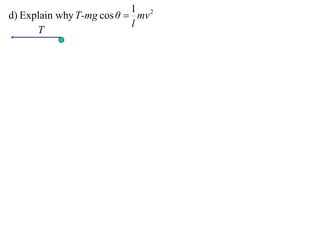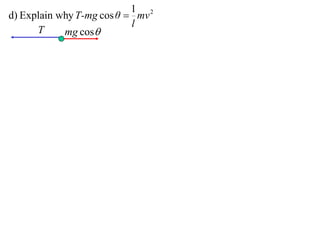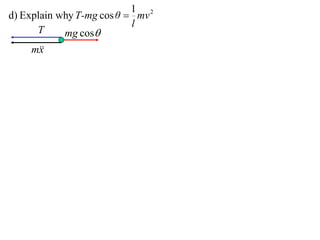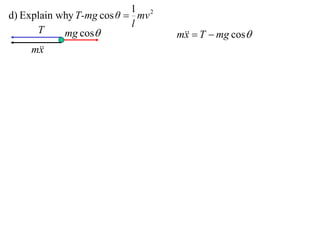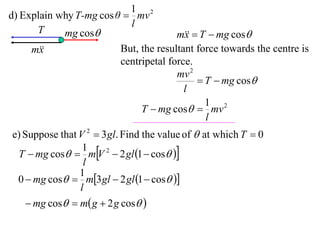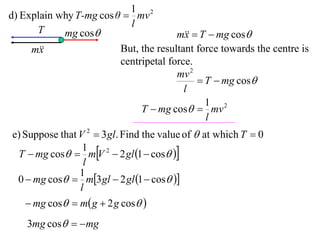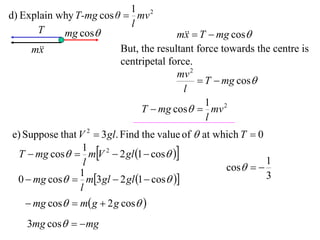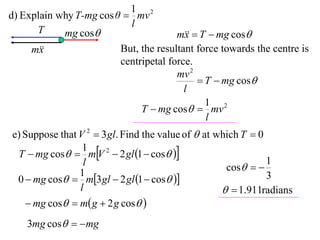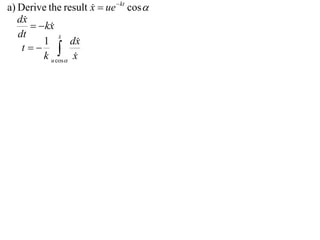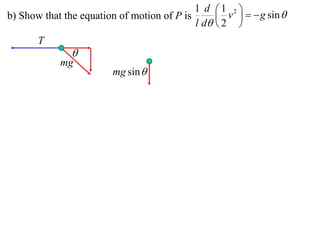
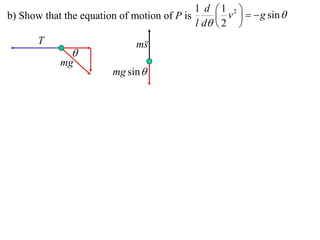
1) The document discusses the motion of a model train T travelling around a circular track with radius a and constant speed u. It derives an expression for the rate of change of the angle θ between the train and a point N distance x from the track, in terms of a, u, x, and the angle φ between NT and the track. 2) It shows that when the line NT is tangent to the track, the rate of change of φ is 0. 3) The overall document solves various kinematic problems related to the motion of the train T around the circular track.

1. Miscellaneous Dynamics
Questions
e.g. (i) (1992) – variable angular velocity
The diagram shows a model train T that is
moving around a circular track, centre O
and radius a metres.
The train is travelling at a constant speed of
u m/s. The point N is in the same plane as
the track and is x metres from the nearest
point on the track. The line NO produced
meets the track at S.
Let TNS   and TOS   as in the diagram

2. dθ
a) Express in terms of a and u
dt

3. dθ
a) Express in terms of a and u l  a
dt

4. dθ
a) Express in terms of a and u l  a
dt dl d
a
dt dt

5. dθ
a) Express in terms of a and u l  a
dt dl d
a
dt dt
d
ua
dt
d u

dt a

6. dθ
a) Express in terms of a and u l  a
dt dl d
a
dt dt
d
ua
dt
d u

dt a
b) Show that a sin    - x  a sin  0 and deduce that;
d u cos   

dt  x  a  cos   a cos   

7. dθ
a) Express in terms of a and u l  a
dt dl d
a
dt dt
d
ua
dt
d u

dt a
b) Show that a sin    - x  a sin  0 and deduce that;
d u cos   

dt  x  a  cos   a cos   
NTO  TNO  TOS (exterior , OTN )

8. dθ
a) Express in terms of a and u l  a
dt dl d
a
dt dt
d
ua
dt
d u

dt a
b) Show that a sin    - x  a sin  0 and deduce that;
d u cos   

dt  x  a  cos   a cos   
NTO  TNO  TOS (exterior , OTN )
NTO    
NTO    

9. dθ
a) Express in terms of a and u l  a
dt dl d
a
dt dt
d
ua
dt
d u

dt a
b) Show that a sin    - x  a sin  0 and deduce that;
d u cos   

dt  x  a  cos   a cos   
NTO  TNO  TOS (exterior , OTN )
NTO     a ax
In NTO; 
NTO     sin  sin    

10. dθ
a) Express in terms of a and u l  a
dt dl d
a
dt dt
d
ua
dt
d u

dt a
b) Show that a sin    - x  a sin  0 and deduce that;
d u cos   

dt  x  a  cos   a cos   
NTO  TNO  TOS (exterior , OTN )
NTO     a ax
In NTO; 
NTO     sin  sin    
a sin      a  x  sin 
a sin      a  x  sin   0

11. differentiate with respect to t
 d  d   a  x  cos  d  0
a cos     
 dt dt  dt

12. differentiate with respect to t
a cos    d  d   a  x  cos  d  0
 
 dt dt  dt
d d
a cos      a cos     a  x  cos   0
dt dt

13. differentiate with respect to t
a cos    d  d   a  x  cos  d  0
 
 dt dt  dt
d d
a cos      a cos     a  x  cos   0
dt dt
a cos     a  x  cos   d  a cos     u
dt a

14. differentiate with respect to t
a cos    d  d   a  x  cos  d  0
 
 dt dt  dt
d d
a cos      a cos     a  x  cos   0
dt dt
a cos     a  x  cos   d  a cos     u
dt a
d u cos   

dt a cos     a  x  cos 

15. differentiate with respect to t
a cos    d  d   a  x  cos  d  0
 
 dt dt  dt
d d
a cos      a cos     a  x  cos   0
dt dt
a cos     a  x  cos   d  a cos     u
dt a
d u cos   

dt a cos     a  x  cos 
d
c) Show that  0 when NT is tangential to the track.
dt
when NT is a tangent;

16. differentiate with respect to t
a cos    d  d   a  x  cos  d  0
 
 dt dt  dt
d d
a cos      a cos     a  x  cos   0
dt dt
a cos     a  x  cos   d  a cos     u
dt a
d u cos   

dt a cos     a  x  cos 
d
c) Show that  0 when NT is tangential to the track.
dt T
N O

17. differentiate with respect to t
a cos    d  d   a  x  cos  d  0
 
 dt dt  dt
d d
a cos      a cos     a  x  cos   0
dt dt
a cos     a  x  cos   d  a cos     u
dt a
d u cos   

dt a cos     a  x  cos 
d
c) Show that  0 when NT is tangential to the track.
dt T
when NT is a tangent;
N O

18. differentiate with respect to t
a cos    d  d   a  x  cos  d  0
 
 dt dt  dt
d d
a cos      a cos     a  x  cos   0
dt dt
a cos     a  x  cos   d  a cos     u
dt a
d u cos   

dt a cos     a  x  cos 
d
c) Show that  0 when NT is tangential to the track.
dt T
when NT is a tangent;
NTO  90 (tangent  radius)
N O

19. differentiate with respect to t
a cos    d  d   a  x  cos  d  0
 
 dt dt  dt
d d
a cos      a cos     a  x  cos   0
dt dt
a cos     a  x  cos   d  a cos     u
dt a
d u cos   

dt a cos     a  x  cos 
d
c) Show that  0 when NT is tangential to the track.
dt T
when NT is a tangent;
NTO  90 (tangent  radius)
N O
    90

20. differentiate with respect to t
a cos    d  d   a  x  cos  d  0
 
 dt dt  dt
d d
a cos      a cos     a  x  cos   0
dt dt
a cos     a  x  cos   d  a cos     u
dt a
d u cos   

dt a cos     a  x  cos 
d
c) Show that  0 when NT is tangential to the track.
dt T
when NT is a tangent;
NTO  90 (tangent  radius)
N O
    90
d u cos 90

dt a cos 90  a  x  cos 

21. differentiate with respect to t
a cos    d  d   a  x  cos  d  0
 
 dt dt  dt
d d
a cos      a cos     a  x  cos   0
dt dt
a cos     a  x  cos   d  a cos     u
dt a
d u cos   

dt a cos     a  x  cos 
d
c) Show that  0 when NT is tangential to the track.
dt T
when NT is a tangent;
NTO  90 (tangent  radius)
N O
    90
d u cos 90 d
  0
dt a cos 90  a  x  cos  dt

22. d) Suppose that x = a
 3
Show that the train’s angular velocity about N when   is
times the angular velocity about N when   0 2 5

23. d) Suppose that x = a
 3
Show that the train’s angular velocity about N when   is
times the angular velocity about N when   0 2 5

when  
2

24. d) Suppose that x = a
 3
Show that the train’s angular velocity about N when   is
times the angular velocity about N when   0 2 5

when  
2
T

N O

25. d) Suppose that x = a
 3
Show that the train’s angular velocity about N when   is
times the angular velocity about N when   0 2 5

when  
2
T
a

N O

26. d) Suppose that x = a
 3
Show that the train’s angular velocity about N when   is
times the angular velocity about N when   0 2 5

when  
2
T
a

N O
2a

27. d) Suppose that x = a
 3
Show that the train’s angular velocity about N when   is
times the angular velocity about N when   0 2 5

when  
2
T
5a a

N O
2a

28. d) Suppose that x = a
 3
Show that the train’s angular velocity about N when   is
times the angular velocity about N when   0 2 5

when  
2
T 2
cos  
5a 5
a

N O
2a

29. d) Suppose that x = a
 3
Show that the train’s angular velocity about N when   is
times the angular velocity about N when   0 2 5

when  
2
T 2
cos  
5a 5
a

 cos    

 1
N
2a
O 2  5

30. d) Suppose that x = a
 3
Show that the train’s angular velocity about N when   is
times the angular velocity about N when   0 2 5

when  
  
2
T u cos 
2 d 2 
cos   
5 dt  
5a a a cos     2a cos 
2 

 cos    

 1
N
2a
O 2  5

31. d) Suppose that x = a
 3
Show that the train’s angular velocity about N when   is
times the angular velocity about N when   0 2 5

when  
  
2
T u cos 
2 d 2 
cos   
5 dt  
5a a a cos     2a cos 
2 

cos    
1
    1 
N
2a
O 2  5 u 
  5
 1   2a  2 
a    
 5  5

32. d) Suppose that x = a
 3
Show that the train’s angular velocity about N when   is
times the angular velocity about N when   0 2 5

when  
  
2
T u cos 
2 d 2 
cos   
5 dt  
5a a a cos     2a cos 
2 

cos    
1
    1 
N
2a
O 2  5 u 
  5
 1   2a  2 
a    
 5  5
u

5a

33. d) Suppose that x = a
 3
Show that the train’s angular velocity about N when   is
times the angular velocity about N when   0 2 5

when  
  
2
T u cos 
2 d 2 
cos   
5 dt  
5a a a cos     2a cos 
2 

cos    
1
    1 
N
2a
O 2  5 u 
  5
when   0  1   2a  2 
a    
 5  5
u

5a

34. d) Suppose that x = a
 3
Show that the train’s angular velocity about N when   is
times the angular velocity about N when   0 2 5

when  
  
2
T u cos 
2 d 2 
cos   
5 dt  
5a a a cos     2a cos 
2 

cos    
1
    1 
N
2a
O 2  5 u 
  5
when   0  1   2a  2 
a    
d u cos 0  5  5

dt a cos 0  2a cos 0 u

5a

35. d) Suppose that x = a
 3
Show that the train’s angular velocity about N when   is
times the angular velocity about N when   0 2 5

when  
  
2
T u cos 
2 d 2 
cos   
5 dt  
5a a a cos     2a cos 
2 

cos    
1
    1 
N
2a
O 2  5 u 
  5
when   0  1   2a  2 
a    
d u cos 0  5  5

dt a cos 0  2a cos 0 u
u 
 5a
3a

36. d) Suppose that x = a
 3
Show that the train’s angular velocity about N when   is
times the angular velocity about N when   0 2 5

when  
  
2
T u cos 
2 d 2 
cos   
5 dt  
5a a a cos     2a cos 
2 

cos    
1
    1 
N
2a
O 2  5 u 
  5
when   0  1   2a  2 
a    
d u cos 0  5  5

dt a cos 0  2a cos 0 u
u 
 5a
3a
5 u
 
3 5a

37. d) Suppose that x = a
 3
Show that the train’s angular velocity about N when   is
times the angular velocity about N when   0 2 5

when  
  
2
T u cos 
2 d 2 
cos   
5 dt  
5a a a cos     2a cos 
2 

cos    
1
    1 
N
2a
O 2  5 u 
  5
when   0  1   2a  2 
a    
d u cos 0  5  5

dt a cos 0  2a cos 0 u
u 
 5a
3a  3
Thus the angular velocity when   is times
5 u 2 5
 
3 5a the angular velocity when   0

38. (ii) (2000) A string of length l is initially vertical and has a mass
P of m kg attached to it. The mass P is given a
horizontal velocity of magnitude V and begins to
move along the arc of a circle in a counterclockwise
direction.
Let O be the centre of this circle and A the initial
ds
position of P. Let s denote the arc length AP, v  ,
dt
  AOP and let the tension in the string be T. The acceleration due to
gravity is g and there are no frictional forces acting on P.
For parts a) to d), assume the mass is moving along the circle.

39. (ii) (2000) A string of length l is initially vertical and has a mass
P of m kg attached to it. The mass P is given a
horizontal velocity of magnitude V and begins to
move along the arc of a circle in a counterclockwise
direction.
Let O be the centre of this circle and A the initial
ds
position of P. Let s denote the arc length AP, v  ,
dt
  AOP and let the tension in the string be T. The acceleration due to
gravity is g and there are no frictional forces acting on P.
For parts a) to d), assume the mass is moving along the circle.
d 2s 1 d  1 2 
a) Show that the tangential acceleration of P is given by 2   v 
dt l d  2 

40. (ii) (2000) A string of length l is initially vertical and has a mass
P of m kg attached to it. The mass P is given a
horizontal velocity of magnitude V and begins to
move along the arc of a circle in a counterclockwise
direction.
Let O be the centre of this circle and A the initial
ds
position of P. Let s denote the arc length AP, v  ,
dt
  AOP and let the tension in the string be T. The acceleration due to
gravity is g and there are no frictional forces acting on P.
For parts a) to d), assume the mass is moving along the circle.
d 2s 1 d  1 2 
a) Show that the tangential acceleration of P is given by 2   v 
dt l d  2 
s  l

41. (ii) (2000) A string of length l is initially vertical and has a mass
P of m kg attached to it. The mass P is given a
horizontal velocity of magnitude V and begins to
move along the arc of a circle in a counterclockwise
direction.
Let O be the centre of this circle and A the initial
ds
position of P. Let s denote the arc length AP, v  ,
dt
  AOP and let the tension in the string be T. The acceleration due to
gravity is g and there are no frictional forces acting on P.
For parts a) to d), assume the mass is moving along the circle.
d 2s 1 d  1 2 
a) Show that the tangential acceleration of P is given by 2   v 
dt l d  2 
s  l
ds
v
dt
d
l
dt

42. (ii) (2000) A string of length l is initially vertical and has a mass
P of m kg attached to it. The mass P is given a
horizontal velocity of magnitude V and begins to
move along the arc of a circle in a counterclockwise
direction.
Let O be the centre of this circle and A the initial
ds
position of P. Let s denote the arc length AP, v  ,
dt
  AOP and let the tension in the string be T. The acceleration due to
gravity is g and there are no frictional forces acting on P.
For parts a) to d), assume the mass is moving along the circle.
d 2s 1 d  1 2 
a) Show that the tangential acceleration of P is given by 2   v 
dt l d  2 
s  l d s dv
2

ds dt 2
dt
v
dt
d
l
dt

43. (ii) (2000) A string of length l is initially vertical and has a mass
P of m kg attached to it. The mass P is given a
horizontal velocity of magnitude V and begins to
move along the arc of a circle in a counterclockwise
direction.
Let O be the centre of this circle and A the initial
ds
position of P. Let s denote the arc length AP, v  ,
dt
  AOP and let the tension in the string be T. The acceleration due to
gravity is g and there are no frictional forces acting on P.
For parts a) to d), assume the mass is moving along the circle.
d 2s 1 d  1 2 
a) Show that the tangential acceleration of P is given by 2   v 
dt l d  2 
s  l d s dv
2

ds dt 2
dt
v dv d
dt  
d d dt
l
dt

44. (ii) (2000) A string of length l is initially vertical and has a mass
P of m kg attached to it. The mass P is given a
horizontal velocity of magnitude V and begins to
move along the arc of a circle in a counterclockwise
direction.
Let O be the centre of this circle and A the initial
ds
position of P. Let s denote the arc length AP, v  ,
dt
  AOP and let the tension in the string be T. The acceleration due to
gravity is g and there are no frictional forces acting on P.
For parts a) to d), assume the mass is moving along the circle.
d 2s 1 d  1 2 
a) Show that the tangential acceleration of P is given by 2   v 
dt l d  2 
s  l d s dv
2

ds dt 2
dt
v dv d
dt  
d d dt
l
dt dv v
 
d l

45. (ii) (2000) A string of length l is initially vertical and has a mass
P of m kg attached to it. The mass P is given a
horizontal velocity of magnitude V and begins to
move along the arc of a circle in a counterclockwise
direction.
Let O be the centre of this circle and A the initial
ds
position of P. Let s denote the arc length AP, v  ,
dt
  AOP and let the tension in the string be T. The acceleration due to
gravity is g and there are no frictional forces acting on P.
For parts a) to d), assume the mass is moving along the circle.
d 2s 1 d  1 2 
a) Show that the tangential acceleration of P is given by 2   v 
dt l d  2 
s  l d s dv
2 1 dv
  v

ds dt 2 dt l d
v dv d
dt  
d d dt
l
dt dv v
 
d l

46. (ii) (2000) A string of length l is initially vertical and has a mass
P of m kg attached to it. The mass P is given a
horizontal velocity of magnitude V and begins to
move along the arc of a circle in a counterclockwise
direction.
Let O be the centre of this circle and A the initial
ds
position of P. Let s denote the arc length AP, v  ,
dt
  AOP and let the tension in the string be T. The acceleration due to
gravity is g and there are no frictional forces acting on P.
For parts a) to d), assume the mass is moving along the circle.
d 2s 1 d  1 2 
a) Show that the tangential acceleration of P is given by 2   v 
dt l d  2 
s  l d s dv
2 1 dv
  v

ds dt 2 dt l d
v 1 dv d 1
dt dv d     v2   
  l d dv  2 
d d dt
l
dt dv v
 
d l

47. (ii) (2000) A string of length l is initially vertical and has a mass
P of m kg attached to it. The mass P is given a
horizontal velocity of magnitude V and begins to
move along the arc of a circle in a counterclockwise
direction.
Let O be the centre of this circle and A the initial
ds
position of P. Let s denote the arc length AP, v  ,
dt
  AOP and let the tension in the string be T. The acceleration due to
gravity is g and there are no frictional forces acting on P.
For parts a) to d), assume the mass is moving along the circle.
d 2s 1 d  1 2 
a) Show that the tangential acceleration of P is given by 2   v 
dt l d  2 
s  l d s dv
2 1 dv
  v

ds dt 2 dt l d
v 1 dv d 1
dt dv d     v2   
  l d dv  2 
d d dt
l 1 d 1 2 
dt dv v   v 
  l d  2 
d l

48. 1 d 1 2 
b) Show that the equation of motion of P is  v    g sin 
l d  2 

49. 1 d 1 2 
b) Show that the equation of motion of P is  v    g sin 
l d  2 

50. 1 d 1 2 
b) Show that the equation of motion of P is  v    g sin 
l d  2 
T

51. 1 d 1 2 
b) Show that the equation of motion of P is  v    g sin 
l d  2 
T
mg

52. 1 d 1 2 
b) Show that the equation of motion of P is  v    g sin 
l d  2 
T

mg

53. 1 d 1 2 
b) Show that the equation of motion of P is  v    g sin 
l d  2 
T

mg
mg sin 

54. 1 d 1 2 
b) Show that the equation of motion of P is  v    g sin 
l d  2 
T m
s

mg
mg sin 

55. 1 d 1 2 
b) Show that the equation of motion of P is  v    g sin 
l d  2 
T m
s m   mg sin 
s

mg
mg sin 

56. 1 d 1 2 
b) Show that the equation of motion of P is  v    g sin 
l d  2 
T m
s m   mg sin 
s

mg    g sin 
s
mg sin 

57. 1 d 1 2 
b) Show that the equation of motion of P is  v    g sin 
l d  2 
T m
s m   mg sin 
s

mg    g sin 
s
mg sin 
1 d 1 2 
 v    g sin 
l d  2 

58. 1 d 1 2 
b) Show that the equation of motion of P is  v    g sin 
l d  2 
T m
s m   mg sin 
s

mg    g sin 
s
mg sin 
1 d 1 2 
 v    g sin 
l d  2 
c) Deduce that V 2  v 2  2 gl 1  cos 

59. 1 d 1 2 
b) Show that the equation of motion of P is  v    g sin 
l d  2 
T m
s m   mg sin 
s

mg    g sin 
s
mg sin 
1 d 1 2 
 v    g sin 
l d  2 
c) Deduce that V 2  v 2  2 gl 1  cos 
1 d 1 2 
 v    g sin 
l d  2 

60. 1 d 1 2 
b) Show that the equation of motion of P is  v    g sin 
l d  2 
T m
s m   mg sin 
s

mg    g sin 
s
mg sin 
1 d 1 2 
 v    g sin 
l d  2 
c) Deduce that V 2  v 2  2 gl 1  cos 
1 d 1 2 
 v    g sin 
l d  2 
d 1 2 
 v    gl sin 
d  2 

61. 1 d 1 2 
b) Show that the equation of motion of P is  v    g sin 
l d  2 
T m
s m   mg sin 
s

mg    g sin 
s
mg sin 
1 d 1 2 
 v    g sin 
l d  2 
c) Deduce that V 2  v 2  2 gl 1  cos 
1 d 1 2 
 v    g sin 
l d  2 
d 1 2 
 v    gl sin 
d  2 
1 2
v  gl cos  c
2
v 2  2 gl cos  c

62. 1 d 1 2 
b) Show that the equation of motion of P is  v    g sin 
l d  2 
T m
s m   mg sin 
s

mg    g sin 
s
mg sin 
1 d 1 2 
 v    g sin 
l d  2 
c) Deduce that V 2  v 2  2 gl 1  cos 
when   0, v  V
1 d 1 2 
 v    g sin  V 2  2 gl  c
l d  2 
c  V 2  2 gl
d 1 2 
 v    gl sin 
d  2 
1 2
v  gl cos  c
2
v 2  2 gl cos  c

63. 1 d 1 2 
b) Show that the equation of motion of P is  v    g sin 
l d  2 
T m
s m   mg sin 
s

mg    g sin 
s
mg sin 
1 d 1 2 
 v    g sin 
l d  2 
c) Deduce that V 2  v 2  2 gl 1  cos 
when   0, v  V
1 d 1 2 
 v    g sin  V 2  2 gl  c
l d  2 
c  V 2  2 gl
d 1 2 
 v    gl sin  v 2  2 gl cos  V 2  2 gl
d  2 
1 2 V 2  v 2  2 gl  2 gl cos
v  gl cos  c
2 V 2  v 2  2 gl 1  cos 
v 2  2 gl cos  c

64. 1 2
d) Explain why T-mg cos θ  mv
l

65. 1 2
d) Explain why T-mg cos θ  mv
l

66. 1 2
d) Explain why T-mg cos θ  mv
l
T

67. 1 2
d) Explain why T-mg cos θ  mv
l
T mg cos

68. 1 2
d) Explain why T-mg cos θ  mv
l
T mg cos
m
x

69. 1 2
d) Explain why T-mg cos θ  mv
l
T mg cos m  T  mg cos
x
m
x

70. 1 2
d) Explain why T-mg cos θ  mv
l
T mg cos m  T  mg cos
x
m
x But, the resultant force towards the centre is
centripetal force.

71. 1 2
d) Explain why T-mg cos θ  mv
l
T mg cos m  T  mg cos
x
m
x But, the resultant force towards the centre is
centripetal force.
mv 2
 T  mg cos
l
1 2
T  mg cos  mv
l

72. 1 2
d) Explain why T-mg cos θ  mv
l
T mg cos m  T  mg cos
x
m
x But, the resultant force towards the centre is
centripetal force.
mv 2
 T  mg cos
l
1 2
T  mg cos  mv
l
e) Suppose that V 2  3 gl. Find the value of  at which T  0

73. 1 2
d) Explain why T-mg cos θ  mv
l
T mg cos m  T  mg cos
x
m
x But, the resultant force towards the centre is
centripetal force.
mv 2
 T  mg cos
l
1 2
T  mg cos  mv
l
e) Suppose that V 2  3 gl. Find the value of  at which T  0
T  mg cos  mV 2  2 gl 1  cos 
1
l

74. 1 2
d) Explain why T-mg cos θ  mv
l
T mg cos m  T  mg cos
x
m
x But, the resultant force towards the centre is
centripetal force.
mv 2
 T  mg cos
l
1 2
T  mg cos  mv
l
e) Suppose that V 2  3 gl. Find the value of  at which T  0
T  mg cos  mV 2  2 gl 1  cos 
1
l
1
0  mg cos  m3 gl  2 gl 1  cos 
l

75. 1 2
d) Explain why T-mg cos θ  mv
l
T mg cos m  T  mg cos
x
m
x But, the resultant force towards the centre is
centripetal force.
mv 2
 T  mg cos
l
1 2
T  mg cos  mv
l
e) Suppose that V 2  3 gl. Find the value of  at which T  0
T  mg cos  mV 2  2 gl 1  cos 
1
l
1
0  mg cos  m3 gl  2 gl 1  cos 
l
 mg cos  m g  2 g cos 

76. 1 2
d) Explain why T-mg cos θ  mv
l
T mg cos m  T  mg cos
x
m
x But, the resultant force towards the centre is
centripetal force.
mv 2
 T  mg cos
l
1 2
T  mg cos  mv
l
e) Suppose that V 2  3 gl. Find the value of  at which T  0
T  mg cos  mV 2  2 gl 1  cos 
1
l
1
0  mg cos  m3 gl  2 gl 1  cos 
l
 mg cos  m g  2 g cos 
3mg cos   mg

77. 1 2
d) Explain why T-mg cos θ  mv
l
T mg cos m  T  mg cos
x
m
x But, the resultant force towards the centre is
centripetal force.
mv 2
 T  mg cos
l
1 2
T  mg cos  mv
l
e) Suppose that V 2  3 gl. Find the value of  at which T  0
T  mg cos  mV 2  2 gl 1  cos 
1
l cos  
1
1
0  mg cos  m3 gl  2 gl 1  cos  3
l
 mg cos  m g  2 g cos 
3mg cos   mg

78. 1 2
d) Explain why T-mg cos θ  mv
l
T mg cos m  T  mg cos
x
m
x But, the resultant force towards the centre is
centripetal force.
mv 2
 T  mg cos
l
1 2
T  mg cos  mv
l
e) Suppose that V 2  3 gl. Find the value of  at which T  0
T  mg cos  mV 2  2 gl 1  cos 
1
l cos  
1
1
0  mg cos  m3 gl  2 gl 1  cos  3
l   1.911radians
 mg cos  m g  2 g cos 
3mg cos   mg

79. f) Consider the situation in part e). Briefly describe, in words, the path of
P after the tension T becomes zero.

80. f) Consider the situation in part e). Briefly describe, in words, the path of
P after the tension T becomes zero.
When T = 0, the particle would undergo projectile motion, i.e. it
would follow a parabolic arc.
Its initial velocity would be tangential to the circle with magnitude;

81. f) Consider the situation in part e). Briefly describe, in words, the path of
P after the tension T becomes zero.
When T = 0, the particle would undergo projectile motion, i.e. it
would follow a parabolic arc.
Its initial velocity would be tangential to the circle with magnitude;
1 2
T  mg cos  mv
l

82. f) Consider the situation in part e). Briefly describe, in words, the path of
P after the tension T becomes zero.
When T = 0, the particle would undergo projectile motion, i.e. it
would follow a parabolic arc.
Its initial velocity would be tangential to the circle with magnitude;
1 2
T  mg cos  mv
l
  1   1 mv 2
 mg  
 3 l

83. f) Consider the situation in part e). Briefly describe, in words, the path of
P after the tension T becomes zero.
When T = 0, the particle would undergo projectile motion, i.e. it
would follow a parabolic arc.
Its initial velocity would be tangential to the circle with magnitude;
1 2
T  mg cos  mv
l
  1   1 mv 2
 mg  
 3 l
gl
v2 
3
gl
v
3

84. f) Consider the situation in part e). Briefly describe, in words, the path of
P after the tension T becomes zero.
When T = 0, the particle would undergo projectile motion, i.e. it
would follow a parabolic arc.
Its initial velocity would be tangential to the circle with magnitude;
1 2
T  mg cos  mv
l
  1   1 mv 2
 mg  
 3 l
gl
v2 
3
gl
v
3

85. f) Consider the situation in part e). Briefly describe, in words, the path of
P after the tension T becomes zero.
When T = 0, the particle would undergo projectile motion, i.e. it
would follow a parabolic arc.
Its initial velocity would be tangential to the circle with magnitude;
1 2
T  mg cos  mv
l
  1   1 mv 2
 mg  
 3 l
gl
v2 
3
gl
v
3

86. f) Consider the situation in part e). Briefly describe, in words, the path of
P after the tension T becomes zero.
When T = 0, the particle would undergo projectile motion, i.e. it
would follow a parabolic arc.
Its initial velocity would be tangential to the circle with magnitude;
1 2
T  mg cos  mv
l
  1   1 mv 2
 mg  
 3 l
gl
v2 
3
gl
v
3

87. f) Consider the situation in part e). Briefly describe, in words, the path of
P after the tension T becomes zero.
When T = 0, the particle would undergo projectile motion, i.e. it
would follow a parabolic arc.
Its initial velocity would be tangential to the circle with magnitude;
1 2
T  mg cos  mv
l
  1   1 mv 2
 mg  
 3 l
gl
v2 
3
gl
v
3

88. f) Consider the situation in part e). Briefly describe, in words, the path of
P after the tension T becomes zero.
When T = 0, the particle would undergo projectile motion, i.e. it
would follow a parabolic arc.
Its initial velocity would be tangential to the circle with magnitude;
1 2
T  mg cos  mv
l
  1   1 mv 2
 mg  
 3 l
gl
v2 
3
gl
v
3

89. (iii) (2003)
A particle of mass m is thrown from the top, O, of a very tall building
with an initial velocity u at an angle of  to the horizontal. The
particle experiences the effect of gravity, and a resistance
proportional to its velocity in both directions.
The equations of motion in the horizontal and
vertical directions are given respectively by
   kx and    ky  g
x  y 
where k is a constant and the acceleration due
to gravity is g.
(You are NOT required to show these)

90. a) Derive the result x  ue  kt cos 


91. a) Derive the result x  ue  kt cos 

dx

  kx

dt

92. a) Derive the result x  ue  kt cos 

dx

  kx

dt x

1 dx
t 
k u cos x


93. a) Derive the result x  ue  kt cos 

dx
  kx

dt x

1 dx 
t 
k u cos x
1
t   log x u cos
x


k

94. a) Derive the result x  ue  kt cos 

dx
  kx

dt x

1 dx 
t 
k u cos x
1
t   log x u cos
x


k
1
t   log x  logu cos  

k

95. a) Derive the result x  ue  kt cos 
 x 
t   log
1 
dx  
  kx
 k  u cos  
dt x

1 dx 
t 
k u cos x
1
t   log x u cos
x


k
1
t   log x  logu cos  

k

96. a) Derive the result x  ue  kt cos 
 x 
t   log
1 
dx  
  kx
 k  u cos  
dt x

1 dx   x  
t   kt  log 
k u cos x  u cos  
1 x

t   log x u cos  e  kt
x


k u cos 
1
t   log x  logu cos  
 x  ue  kt cos 

k

97. a) Derive the result x  ue  kt cos 
 x 
t   log
1 
dx  
  kx
 k  u cos  
dt x

1 dx  x  
t   kt  log 
k u cos x  u cos  
1 x

t   log x u cos  e  kt
x


k u cos 
1
t   log x  logu cos  
 x  ue  kt cos 

k
b) Verify that y  ku sin   g e  kt  g  satisfies the appropriate
1

k
equation of motion and initial condition

98. a) Derive the result x  ue  kt cos 
 x 
t   log
1 
dx  
  kx
 k  u cos  
dt x

1 dx  x  
t   kt  log 
k u cos x  u cos  
1 x

t   log x u cos  e  kt
x


k u cos 
1
t   log x  logu cos  
 x  ue  kt cos 

k
b) Verify that y  ku sin   g e  kt  g  satisfies the appropriate
1

k
equation of motion and initial condition
dy
  ky  g

dt

99. a) Derive the result x  ue  kt cos 
 x 
t   log
1 
dx  
  kx  k  u cos  
dt x

1 dx  x  
t   kt  log 
k u cos x   u cos  
1 x

t   log x u cos  e  kt
x


k u cos 
1
t   log x  logu cos  
 x  ue  kt cos 

k
b) Verify that y  ku sin   g e  kt  g  satisfies the appropriate
1

k
equation of motion and initial condition
dy
  ky  g

dt y
dy
t 
u sin 
ky  g


100. a) Derive the result x  ue  kt cos 
 x 
t   log
1 
dx  
  kx  k  u cos  
dt x

1 dx  x  
t   kt  log 
k u cos x   u cos  
1 x

t   log x u cos  e  kt
x


k u cos 
1
t   log x  logu cos  
 x  ue  kt cos 

k
b) Verify that y  ku sin   g e  kt  g  satisfies the appropriate
1

k
equation of motion and initial condition
dy
  ky  g

dt y
dy
t 
u sin 
ky  g

1
t   logky  g u sin 
y


k

101. a) Derive the result x  ue  kt cos 
 x 
t   log
1 
dx  
  kx  k  u cos  
dt x

1 dx  x  
t   kt  log 
k u cos x   u cos  
1 x

t   log x u cos  e  kt
x


k u cos 
1
t   log x  logu cos  
 x  ue  kt cos 

k
b) Verify that y  ku sin   g e  kt  g  satisfies the appropriate
1

k
equation of motion and initial condition
dy  kt  logky  g   logku sin   g 
  ky  g
 
dt y
dy
t 
u sin 
ky  g

1
t   logky  g u sin 
y


k

102. a) Derive the result x  ue  kt cos 
 x 
t   log
1 
dx  
  kx  k  u cos  
dt x

1 dx  x  
t   kt  log 
k u cos x   u cos  
1 x

t   log x u cos  e  kt
x


k u cos 
1
t   log x  logu cos  
 x  ue  kt cos 

k
b) Verify that y  ku sin   g e  kt  g  satisfies the appropriate
1

k
equation of motion and initial condition
dy  kt  logky  g   logku sin   g 
  ky  g
 
dt y  ky  g 
dy  kt  log 
t   ku sin   g 
u sin 
ky  g

1
t   logky  g u sin 
y


k

103. a) Derive the result x  ue  kt cos 
 x 
t   log
1 
dx  
  kx  k  u cos  
dt x

1 dx  x  
t   kt  log 
k u cos x   u cos  
1 x

t   log x u cos  e  kt
x


k u cos 
1
t   log x  logu cos  
 x  ue  kt cos 

k
b) Verify that y  ku sin   g e  kt  g  satisfies the appropriate
1

k
equation of motion and initial condition
dy  kt  logky  g   logku sin   g 
  ky  g
 
dt y  ky  g 
dy  kt  log 
t   ku sin   g 
u sin 
ky  g
 ky  g

 e  kt
1
t   logky  g u sin 

y
 ku sin   g
k

104. a) Derive the result x  ue  kt cos 
 x 
t   log
1 
dx  
  kx  k  u cos  
dt x

1 dx  x  
t   kt  log 
k u cos x   u cos  
1 x

t   log x u cos  e  kt
x


k u cos 
1
t   log x  logu cos  
 x  ue  kt cos 

k
b) Verify that y  ku sin   g e  kt  g  satisfies the appropriate
1

k
equation of motion and initial condition
dy  kt  logky  g   logku sin   g 
  ky  g
 
dt y  ky  g 

dy  kt  log 
t   ku sin   g 
u sin 
ky  g
 ky  g

 e  kt
1
t   logky  g u sin 

y
 ku sin   g
y  ku sin   g e  kt  g 
1
k 
k

105. c) Find the value of t when the particle reaches its maximum height

106. c) Find the value of t when the particle reaches its maximum height
Maximum height occurs when y  0


107. c) Find the value of t when the particle reaches its maximum height
Maximum height occurs when y  0

1
t   logky  g u sin 
0

k

108. c) Find the value of t when the particle reaches its maximum height
Maximum height occurs when y  0 
1
t   logky  g u sin 
0

k
1
t   log g   logku sin   g 
k

109. c) Find the value of t when the particle reaches its maximum height
Maximum height occurs when y  0 
1
t   logky  g u sin 
0

k
1
t   log g   logku sin   g 
k
1  ku sin   g 
t  log 
k  g 

110. c) Find the value of t when the particle reaches its maximum height
Maximum height occurs when y  0 
1
t   logky  g u sin 
0

k
1
t   log g   logku sin   g 
k
1  ku sin   g 
t  log 
k  g 
d) What is the limiting value of the horizontal displacement of the
particle?

111. c) Find the value of t when the particle reaches its maximum height
Maximum height occurs when y  0 
1
t   logky  g u sin 
0

k
1
t   log g   logku sin   g 
k
1  ku sin   g 
t  log 
k  g 
d) What is the limiting value of the horizontal displacement of the
particle?
x  ue  kt cos 

dx
 ue  kt cos 
dt

112. c) Find the value of t when the particle reaches its maximum height
Maximum height occurs when y  0 
1
t   logky  g u sin 
0

k
1
t   log g   logku sin   g 
k
1  ku sin   g 
t  log 
k  g 
d) What is the limiting value of the horizontal displacement of the

particle?
x  lim u cos   e  kt dt
x  ue  kt cos 
 t 
0
dx
 ue  kt cos 
dt

113. c) Find the value of t when the particle reaches its maximum height
Maximum height occurs when y  0 
1
t   logky  g u sin 
0

k
1
t   log g   logku sin   g 
k
1  ku sin   g 
t  log 
k  g 
d) What is the limiting value of the horizontal displacement of the

particle?
x  lim u cos   e  kt dt
x  ue  kt cos 
 t 
0
t
dx x  lim u cos   e  kt 
1
 ue cos 
 kt
 k 0
dt t   

114. c) Find the value of t when the particle reaches its maximum height
Maximum height occurs when y  0 
1
t   logky  g u sin 
0

k
1
t   log g   logku sin   g 
k
1  ku sin   g 
t  log 
k  g 
d) What is the limiting value of the horizontal displacement of the

particle?
x  lim u cos   e  kt dt
x  ue  kt cos 
 t 
0
t
dx x  lim u cos   e  kt 
1
 ue cos 
 kt
 k 0
dt t   
u cos 
x  lim  e kt  1
t  k

115. c) Find the value of t when the particle reaches its maximum height
Maximum height occurs when y  0 
1
t   logky  g u sin 
0

k
1
t   log g   logku sin   g 
k
1  ku sin   g 
t  log 
k  g 
d) What is the limiting value of the horizontal displacement of the

particle?
x  lim u cos   e  kt dt
x  ue  kt cos 
 t 
0
t
dx x  lim u cos   e  kt 
1
 ue cos 
 kt
 k 0
dt t   
u cos 
x  lim  e kt  1
t  k
u cos 
x
k

116. Exercise 9E; 1 to 4, 7
Exercise 9F; 1, 2, 4, 7, 9, 12, 14, 16, 20, 22, 25