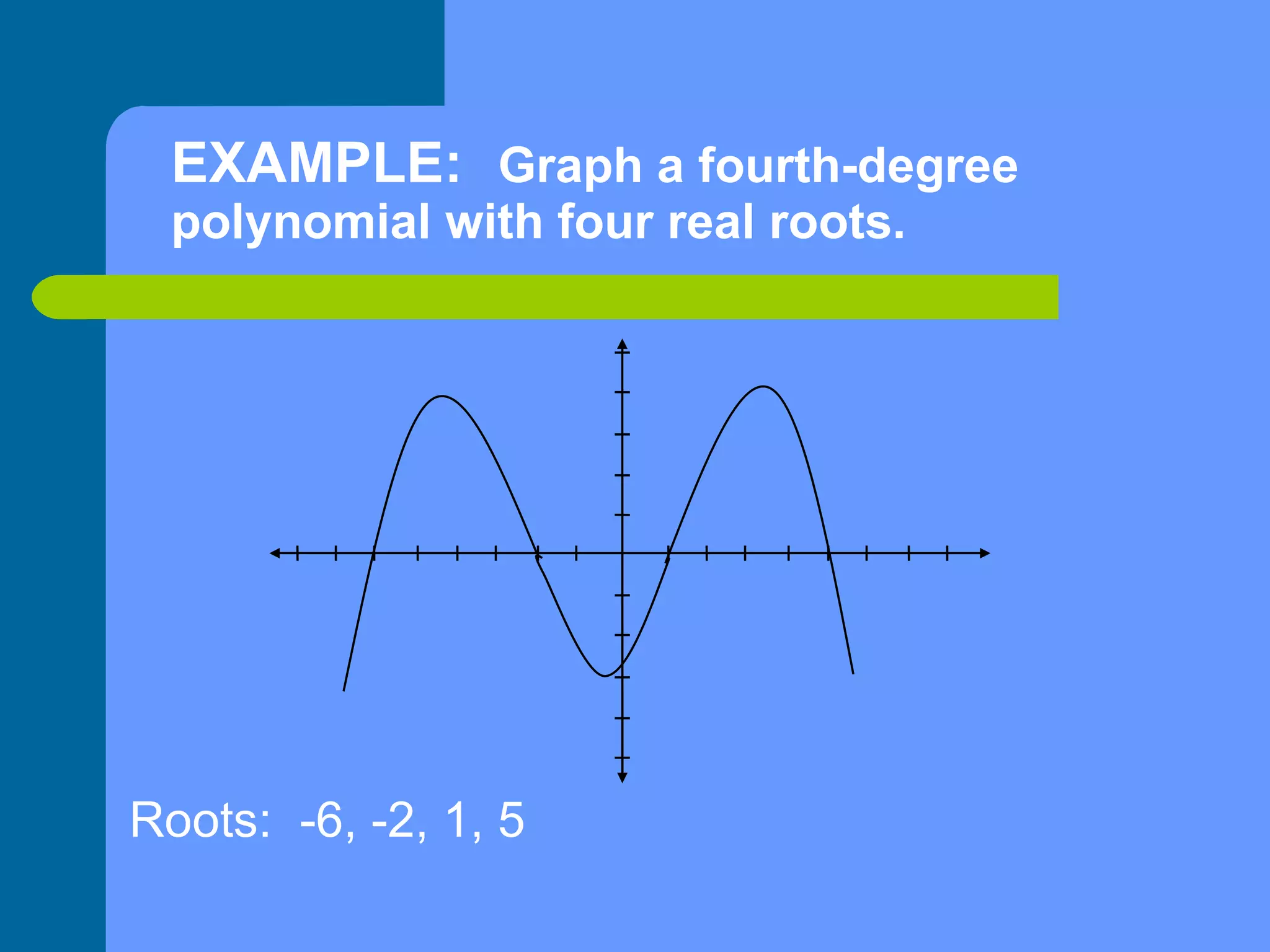
This document provides an example of how to graph and write a polynomial equation given a set of real roots. It shows how to: 1) Write a 4th degree polynomial in standard form given roots of -6, -2, 1, 5. 2) Graph the polynomial by plotting the x-intercepts at the roots and determining the shape of the curve between them. 3) Verify the roots by factoring the polynomial and using synthetic division to show it has factors corresponding to the original roots.

1. Writing and Graphing Polynomial Equations Julie Wagner: Rockledge High School Algebra 2, Advanced Topics, Pre-Calc, Trig/Ananlt Geometry [email_address]

2. Objective: To graph, analyze, write, and describe polynomial equations with real and complex roots. NGSSS: MA.912.A.4.5 Graph polynomial functions with and without technology and describe end behavior. MA.912.A.4.6 Use the Fundamental Theorem of Algebra. MA.912.A.4.7 Write a polynomial equation for a given set of real and/or complex roots.

3. Key Concepts: Roots of a polynomial Describe end behavior Write an equation in standard form from given roots Rational Root Theorem Find the zeros of a polynomial equation Imaginary Roots

4. EXAMPLE: Graph a fourth-degree polynomial with four real roots. Roots: -6, -2, 1, 5

5. Using your roots (zeros) write a polynomial function in standard form. x = -6, -2, 1, 5 F(x) = (x + 6)(x + 2)(x – 1)(x – 5) F(x) = (x 2 + 8x + 12)(x 2 – 6x + 5) F(x) = x 4 – 6x 3 + 5x 2 + 8x 3 – 48x 2 + 40x + 12x 2 - 72x + 60 F(x) = x 4 + 2x 3 – 31x 2 – 32x + 60 Since the right side behavior opens down, we need our leading coefficient negative. Multiply by -1. F(x) = –x 4 – 2x 3 + 31x 2 + 32x – 60

6. Now lets check our work. Work backwards to find the roots F(x) = -x 4 – 2x 3 + 31x 2 + 32x – 60 Use the Rational Root Theorem to list all the possible rational roots. ±1 ±2 ±3 ±4 ±5 ±6 ±10 ±12 ±15± 20 ±30 ±60

7. 1. Use the Rational Root Theorem. ±1 ±2 ±3 ±4 ±5 ±6 ±10 ±12 ±15± 20 ±30 ±60 Use synthetic division with x = 1. 1 -1 -2 31 32 -60 -1 -3 28 60 -1 -3 28 60 0 P(x) = (x – 1)(-x 3 – 3x 2 + 28x + 60)

8. 3. Use synthetic division with x = -2. -2 -1 -3 28 60 2 2 -60 -1 -1 30 0 F(x) = (x – 1)(x + 2)(-x 2 – x + 30) F(x) = (x – 1)(x + 2)(-x + 5)(x + 6) Roots: x = 1, -2, 5, -6

9. The roots should be the same as when you started.

10. DIRECTIONS: Get into groups of 2-4 people. Grab 2 string, scissors, glue bottle, & 4 sheets of graph paper & cut along dotted line. Cut string into 2 equal length pieces. Label the X and Y-Axis. Take 20-30 minutes to construct third and fourth degree polynomial graphs fitting the described roots. Answer the questions that follow.

11. THE END!!! [email_address] Julie Wagner Rockledge High School 321-636-3711 x262