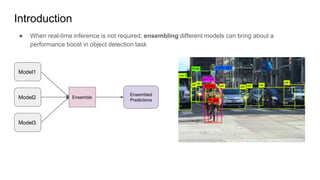
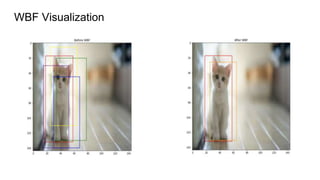
Weighted boxes fusion (WBF) is an object detection ensemble method that averages bounding box predictions from multiple models rather than discarding redundant boxes. It works by clustering overlapping boxes, calculating a weighted average bounding box for each cluster, and rescaling confidence scores based on cluster size. This allows all predictions to contribute to the final output. WBF is shown to outperform non-maximum suppression (NMS) and soft-NMS on ensembles of different object detection models and with test time augmentation, producing more accurate averaged predictions.

1. Weighted boxes fusion: Ensembling boxes from
different object detection models
2022/04/11, Changjin Lee

2. Introduction
● When real-time inference is not required, ensembling different models can bring about a
performance boost in object detection task
Model1
Model2
Model3
Ensembled
Predictions
Ensemble

3. Non-maximum suppression (NMS)
● Sort bounding boxes in decreasing order of their confidence scores
● For each class, starting from the highest-confidence box (box A), remove all the “redundant” boxes
whose IoU with box A > iou_thresh

4. Soft-NMS
● Instead of removing bounding boxes, soft-NMS reduces the confidences of the proposals
proportional to the IoU value
● Soft-NMS shows a noticeable improvement over the plain NMS method

5. Problems with NMS / Soft-NMS
Both NMS and Soft-NMS discard redundant boxes
They cannot produce averaged localization predictions from different models
Q) Rather than discarding “redundant” boxes, why don’t we make all of them to contribute to the prediction?

6. Weighted Boxes Fusion (WBF)
● Unlike NMS and Soft-NMS that discard redundant boxes, WBF makes them to all contribute to the
prediction proportionally to their confidence score, producing an averaged prediction
○ Although each prediction might not be optimal, they must contribute
at least a little bit

7. Step 0 - N Different Models
● Suppose we have bounding boxes for the same image from N different models
● Bounding box coordinates must be normalized
● Construct boxes_list, scores_list, labels_list
model 1
model 2

8. Step 1 - Merge bboxes to B
● Add each predicted box from each model to a single list B
○ Filter boxes with confidence < score_thr
● Sort in decreasing order of the confidence score C
B = [b1, b2, b3, b4]

9. Step 2 - Boxes cluster L / Fused Box F
● Declare an empty list L for boxes clusters - each position of L contains a set of boxes
● Declare an empty list F for fused boxes - each position of F contains a single box
B = [b1, b2, b3, b4]
L = [ ] (2D list)
F = [ ] (1D list)

10. Step 3 - Loop through B and find a match from F
● Iterate through each box in B and find the best matching box in F
○ Highest IoU with B
○ best_iou > iou_thr
B = [b1, b2, b3, b4]
L = [ ]
F = [ ]
B = [b1, b2, b3, b4]
F = [f1, f2, f3]
best_f_idx
best_iou

11. Step 4 - If no match found
● If no match found, add the box from B to the end of lists L and F
● Then, go back to Step 3
● If no match found for all boxes in B, the algorithm never proceeds to the next step
each position of L contains a set of boxes
B = [b1, b2, b3, b4]
L = [ ]
F = [ ]
B = [b1, b2, b3, b4]
L = [[b1]]
F = [b1]

12. Step 5 - If match found
● If match found,
○ Add b_i to L at position best_f_idx corresponding to the matching box in F
B = [b1, b2, b3, b4]
L = [[b1, b2]]
F = [b1]
best_f_idx
B = [b1, b2, b3, b4]
L = [[b1]]
F = [b1]
iou > iou_thr

13. Step 6 - Perform WBF
● Perform WBF on the set of boxes in L which now has one more element
● Fused Confidence Score = Averaged confidence of all boxes from the cluster
● Fused box coordinates = Weighted average of all boxes from the cluster
B = [b1, b2, b3, b4]
L = [[b1, b2]]
F = [b1]
B = [b1, b2, b3, b4]
L = [[b1, b2]]
F = [f1]

14. Step 7 - Re-scale confidence scores in F
● After all boxes in B are processed, re-scale the confidence scores in F by
○ multiply by min(# of boxes in a cluster, N) - len(L[i])
○ divide by a # of models N
● The fused box predicted by many boxes is likely to be more accurate
B = [b1, b2, b3, b4]
L = [[b1, b2, b3], b4]
F = [f1, f2]

15. [No Match]
B = [b1, b2, b3, b4]
L = [ ]
F = [ ]

16. [No Match] - Add to L and F
B = [b1, b2, b3, b4]
L = [[b1]]
F = [b1]

17. [Match]
B = [b1, b2, b3, b4]
L = [[b1]]
F = [b1]
best_f_idx

18. [Match] - Add to L[best_f_idx]
B = [b1, b2, b3, b4]
L = [[b1, b2]]
F = [b1]
best_f_idx

19. [Match] - WBF
B = [b1, b2, b3, b4]
L = [[b1, b2]]
F = [f1]

20. [No Match]
B = [b1, b2, b3, b4]
L = [[b1, b2]]
F = [f1]

21. [No Match] - Add to L and F
B = [b1, b2, b3, b4]
L = [[b1, b2], [b3]]
F = [f1, b3]

22. [Match]
B = [b1, b2, b3, b4]
L = [[b1, b2], [b3]]
F = [f1, b3]
best_f_idx

23. [Match] - Add to L
B = [b1, b2, b3, b4]
L = [[b1, b2, b4], [b3]]
F = [f1, b3]
best_f_idx

24. [Match] - WBF
B = [b1, b2, b3, b4]
L = [[b1, b2, b4], [b3]]
F = [f1’, b3]

25. WBF Visualization

26. Performance: Ensemble of two different models

27. Performance: Ensemble of same model with TTA

28. Performance: Ensemble of many different models

29. Personal Notes
● Section 2.1 NMS IoU threshold
● How does WBF perform better for side-by-side
objects than NMS?

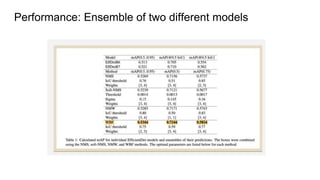
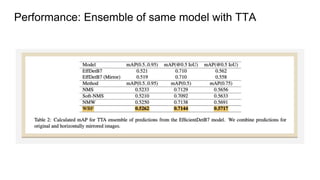
30. References
[1] https://arxiv.org/pdf/1910.13302.pdf
[2] https://github.com/ZFTurbo/Weighted-Boxes-Fusion