次元圧縮周りでの気付き＆１細胞発現データにおける次元圧縮の利用例@第３回wacode
•Download as PPTX, PDF•
6 likes•2,639 views
ほげほげ
More Related Content
What's hot
What's hot (20)
Viewers also liked
Viewers also liked (17)
More from Hirotaka Matsumoto
次元圧縮周りでの気付き＆１細胞発現データにおける次元圧縮の利用例@第３回wacode
- 2. 自己紹介 • 松本 拡高 • 東大 メディカル情報生命専攻 D3 • バイオインフォにおける確率モデル と機械学習 • 連絡先 – @gggtta – matsumoto@cb.k.u-tokyo.ac.jp
- 5. 次元圧縮(PCA)とは • 目的関数による理解 • 元の高次元データXiを、データ共通のWと 低次元Ziを用いて上手く近似できるWとZi を求める。(Wは直交する) • 可視化するときは、たいていZiをplot
- 6. Sparse coding • そもそも、この話をするようになったきっかけ • なんか解釈可能な特徴量(辞書)が出てくるらし い。という話を聞いて調べてみたところ。。。 引用：http://charles.cadieu.us/?p=184
- 7. Sparse coding • 目的関数は • Wの直交性の条件はない • Ziにスパース性を含めただけ • PCAとほとんど同じではないか。。。 • 確率論的には – PCA : ziの事前分布がガウス分布 – SC : ziの事前分布がラプラス分布
- 9. Topic model • topicの出現確率が、文章ごとに違うmixture modelの拡張だと私は最初に思った • 混合モデル：topicの出現確率は一定
- 10. Topic model • でも確率的に解釈すると、次元圧縮にWが B、πiがZiとみなすと、ほぼprobabilistic PCA • 要はZiに、Zi>0かつ足したら１という条件 が加わっただけ
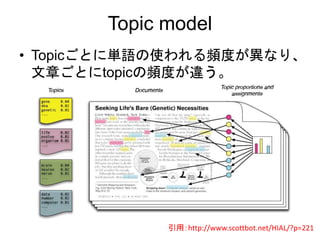
- 11. topic model -> mixture model -> k-means • トピックモデル – 出現確率がデータごとに異なる。 • 混合モデル – 出現確率はデータで共通 • K-means – 混合ガウスのある極限
- 12. Diffusion map • PCAを非線形に拡張したものにdiffusion mapと いうものがある 芳村さんのスライドから拝借
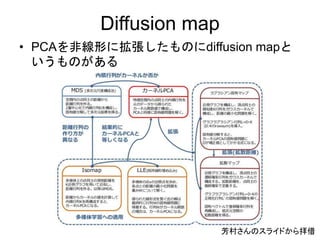
- 13. Diffusion map • 手順 • 高次元空間上でのデータ間の遷移確率行 列をガウスカーネルから作る(ある種のグ ラフラプラシアン) • 遷移確率行列を固有値分解してえられる 固有ベクトルがZiに相当
- 14. Spectral clustering • グラフラプラシアンといえばこいつ • グラフラプラシアンを固有値分解して、固有ベ クトルでk-meansなど 引用：http://d.hatena.ne.jp/mr_r_i_c_e/20121214/1355499195
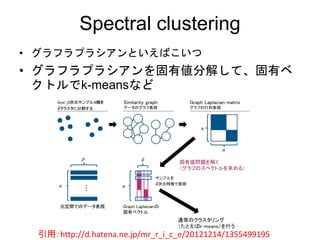
- 15. Diffusion map vs spectral clustering • グラフラプラシアンを固有値分解して固 有ベクトルを見るところまで同じ – ※正確には許容できるグラフラプラシアンが違うはず • 固有ベクトルを、連続量として扱うか、 離散的なクラスタに分類するかの違いで しかない。
- 16. 個人的な俯瞰図(scatter plot) PCA Diffusion map Sparse coding スパース性 非線形 グラフラプラシアンの 固有値分解 クラスタリング K-means Spectral clustering混合モデル 混合ガウス トピックモデル 正則化条件 次元圧縮
- 17. 個人的感想 • いろいろかっこいい名前をつけているが、基 盤はたいてい同じである。 • 次元圧縮もクラスタリングも混合モデルもた いてい同じようなことをしている – 機械学習は案外浅い研究分野？（※学習理論では なく、モデルの多様性という意味で） – いろいろ機械学習の手法を勉強してきたつもりだ けど、実はたいして学んでいない！！？？？ • もっとディープな新しい何かが欲しい。 – ※ただし決してそれはディープラーニングではな い
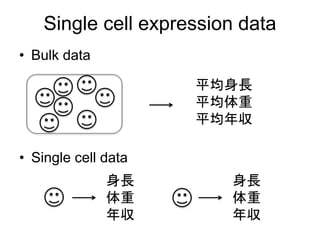
- 19. Single cell expression data • Bulk data – ある程度細胞数が含まれたサンプルをまとめ て計測する – 異なる分化進行度、細胞運命の細胞が混ざっ ており、データは平均像でしかない • Single cell data – 各細胞のデータを取得できるようになった
- 20. Single cell expression data • Bulk data • Single cell data 平均身長 平均体重 平均年収 身長 体重 年収 身長 体重 年収
- 23. １細胞を１個人で考える • １細胞を１個人。遺伝子の発現量を身長 や年収などの特性と考える。 １細胞 発現量 遺伝子1 : 0.3 遺伝子2 : 1.9 1個人 値 身長 : 170 年収 : 300
- 24. 細胞分化を知る、人の成長を知る • 幹細胞→心筋細胞の分化過程を知りたい • 子供→大人の成長過程を知りたい １細胞 発現量 遺伝子1 : 0.3 遺伝子2 : 1.9 1個人 値 身長 : 170 年収 : 300
- 25. 具体的に知りたいのは？ • 各細胞の分化進行度や細胞運命は未知 • 各個人の年齢や職業は未知 １細胞 発現量 遺伝子1 : 0.3 遺伝子2 : 1.9 1個人 値 身長 : 170 年収 : 300
- 27. 次元圧縮を用いた経路再構築とは？ • 分化過程or成長過程を推定する • MST, principal curve, …. 子供 iPS 警察官 心筋細胞 医者 肝細胞
- 29. 次元圧縮の問題点 • 圧縮空間上での経路の生物学的な意味の 解釈が困難 • 必ずしも第１、第２成分が見たいものを 表すわけではない – ノイズに弱く、いろいろぶれる – 第何成分まで見れば良いのか？
- 32. 直接的なモデル化 • 生物学的な機構を考慮したモデル化 • Ornstein-Uhlenbeck process
- 33. 第１回wacodeより再掲 Essentially, all models are wrong, but some are useful. George E. P. Box(18 October 1919 – 28 March 2013)
- 35. まとめ • 教師なし学習は基本的にPCAを基盤とし てちょっと変わってるだけ。 • 次元圧縮は優れた手法だが、万能ではな い – 思考停止をしてはダメ – 直接的なモデル化をぜひ