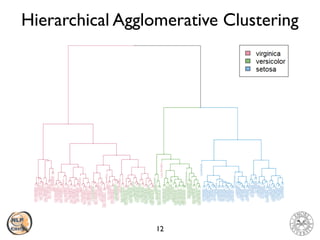
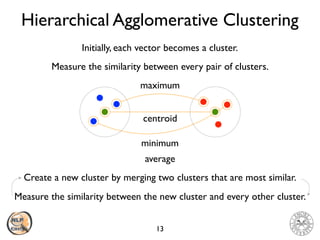
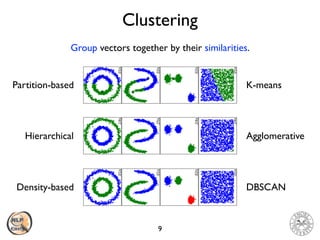
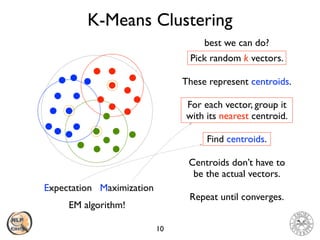
The document discusses vector space models and how they can be used to represent documents numerically. It introduces the bag-of-words model and TF-IDF weighting. It then discusses how cosine similarity and Euclidean distance can be used to calculate similarity between document vectors. Finally, it summarizes several clustering algorithms like k-means, k-means++, and hierarchical agglomerative clustering that can group similar document vectors.

1. Vector Space Models
Natural Language Processing
Emory University
Jinho D. Choi

2. Document Representation
2
How to represent a document in a vector space?
Last
word
First
word
I like this movie very much
Bag-of-Words
0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 01 11 1 1 1
dimension = size of the vocabulary
0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0
I hate this movie so much
1 11 1 11

3. Bag-of-Words
3
Jinho Choi is a professor at Emory University .
Prof. Choi teaches computer science .
Dr. Choi ’s research is on natural language processing .
0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 011 1 1 1 1 1 111 1 11 1 111 1 11
Jinho
Choi
is
a
professor
at
Emory
University
Prof.
.
teaches
computer
science
Dr.
‘s
research
onnatural
language
processing
Are all words equally important?
33
“.”
as important as
“Choi”?
“is”
more important
than “Emory”?
2

4. Term Frequency
Bag-of-Words
4
Jinho Choi is a professor at Emory University .
Prof. Choi teaches computer science .
Dr. Choi ’s research is on natural language processing .
0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0111 3 1 1 1 213 1 11 1 111 1 11
Choi is. Emory
Out of 10 documents:
“.” appears in 10 documents
“Choi” appears in 1 document
“is” appears in 7 documents
“Emory” appears in 2 documents
3 / 10 3 / 1 2 / 7 1 / 2
Document
Frequency

5. TF-IDF
5
Term Frequency of w in d ∈ D = # of times that w appears in d
Given a set of documents D:
Document Frequency of w ∈ D = # of documents that w appears
tf · idfw,d = tfw,d · log
|D|
dfw
Inverse
Document Frequency
wfw,d =
⇢
1 + log tfw,d if tfw,d > 0
0 otherwise
ntfw,d = ↵ + (1 ↵)
tfw,d
tfmax(d)
sublinear
normalized

6. Document Similarity
6
I like this movie very much
Compare two documents in a vector space?
0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 01 11 1 1 1
I hate this movie so much
0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 01 11 1 11
Euclidean distance Cosine similarity
kp qk =
p
2
p · q
kpkkqk
=
4
p
6 ·
p
6
=
2
3

7. Document Similarity
7
0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 01 11 1 11
0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 01 11 1 1 1
0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 03 33 3 3 3
I like this movie very much
I like this movie very much
I like this movie very much
I like this movie very much
I hate this movie so much
euc(p, q) = 2 cos(p, q) = 0.67
r
p
q
r
p
q
θ
0
euc(p, r) = 4.90 cos(p, r) = 1
Magnitude Direction

8. Document Similarity
8
I hate this movie so much I love this movie so muchvs.
q
p
θ1 r
θ2
Shouldn’t this be
more similar?
cos(p, q) ⇡ cos(p, r)
Represent documents
using word embeddings!
I like this movie very much
euc(p, q) ⇡ euc(p, r)

9. Clustering
9
Group vectors together by their similarities.
Partition-based
Hierarchical
Density-based
K-means
Agglomerative
DBSCAN

10. K-Means Clustering
10
Pick random k vectors.
For each vector, group it
with its nearest centroid.
These represent centroids.
Find centroids.
Repeat until converges.
Centroids don’t have to
be the actual vectors.
EM algorithm!
Expectation Maximization
best we can do?

11. K-Means++ Clustering
11
Introduce a random vector c as the first centroid.
Pick a random number r in (0, 1].
D(x) = min
8c
dist(x, c)
Choose xi as the next centroid s.t. C(xi 1) < r  C(xi)
C(xi) =
iX
j=1
P(xj)C(x0) = 0
Measure the distance between every vertex x to its nearest centroid c.
Measure the distance probability for each vertex x.
Measure the cumulative probability for each vertex x.
P(x) =
D(x)2
P
8x D(x)2

12. Hierarchical Agglomerative Clustering
12

13. Hierarchical Agglomerative Clustering
13
Initially, each vector becomes a cluster.
Measure the similarity between every pair of clusters.
Create a new cluster by merging two clusters that are most similar.
Measure the similarity between the new cluster and every other cluster.
maximum
minimum
centroid
average

14. Purity Score
14
How to evaluate clusters?
Count of the genre with the maximum documents
4 3 4
Purity = (4 + 3 + 4) / 19