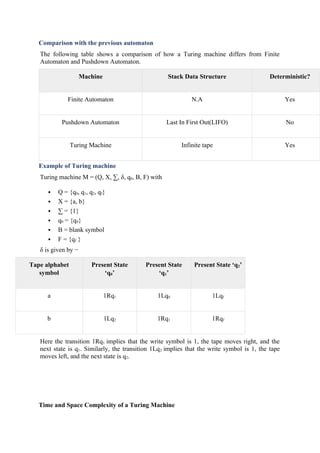
This document discusses Turing machines, their definitions, types (deterministic, non-deterministic), and their role in modeling computation, highlighting the Church-Turing thesis which states that every solvable decision problem can be modeled by a Turing machine. It also explains the components of a Turing machine and introduces the concept of the universal Turing machine, which can simulate any other machine. The document emphasizes the significance of recursively enumerable and context-sensitive languages, as well as time and space complexity in relation to Turing machines.

1. UNIT 5
Turing Machines and Undecidability: Definition, Computing with Turing machine,
Extensions of Turing machines, Random access Turing machines, Non-deterministic Turing
machines, Grammars, The Church’s Turing hypothesis, Universal Turing machines, The
Halting problem, Unsolvable problems about Turing machines.
• Recursively enumerable languages are also known as type 0 languages.
• Context-sensitive languages are also known as type 1 languages.
• Context-free languages are also known as type 2 languages.
Regular languages are also known as type 3 languages
• TMs model the computing capability of a general purpose computer, which
informally can be described as:
– Effective procedure
• Finitely describable
• Well defined, discrete, “mechanical” steps
• Always terminates
– Computable function
• A function computable by an effective procedure
• TMs formalize the above notion.
• Church-Turing Thesis: There is an effective procedure for solving a problem if and
only if there is a TM that halts for all inputs and solves the problem.
– There are many other computing models, but all are equivalent to or subsumed
by TMs. There is no more powerful machine (Technically cannot be proved).
• DFAs and PDAs do not model all effective procedures or computable functions, but
only a subset.

2. ……..
Two-way, infinite tape, broken into cells, each containing one symbol.
• Two-way, read/write tape head.
• An input string is placed on the tape, padded to the left and right infinitely with
blanks, read/write head is positioned at the left end of input string.
• Finite control, i.e., a program, containing the position of the read head, current symbol
being scanned, and the current state.
• In one move, depending on the current state and the current symbol being scanned,
the TM 1) changes state, 2) prints a symbol over the cell being scanned, and 3) moves
its’ tape head one cell left or right.
• Many modifications possible, but Church-Turing declares equivalence of all.
A Turing Machine is an accepting device which accepts the languages (recursively
enumerable set) generated by type 0 grammars. It was invented in 1936 by Alan Turing.
Definition
A Turing Machine (TM) is a mathematical model which consists of an infinite length tape
divided into cells on which input is given. It consists of a head which reads the input tape. A
state register stores the state of the Turing machine. After reading an input symbol, it is
replaced with another symbol, its internal state is changed, and it moves from one cell to the
right or left. If the TM reaches the final state, the input string is accepted, otherwise rejected.
A TM can be formally described as a 7-tuple (Q, X, ∑, δ, q0, B, F) where −
 Q is a finite set of states
 X is the tape alphabet
 ∑ is the input alphabet
 δ is a transition function; δ : Q × X → Q × X × {Left_shift, Right_shift}.
 q0 is the initial state
 B is the blank symbol
 F is the set of final states
Finite
Control

3. Comparison with the previous automaton
The following table shows a comparison of how a Turing machine differs from Finite
Automaton and Pushdown Automaton.
Machine Stack Data Structure Deterministic?
Finite Automaton N.A Yes
Pushdown Automaton Last In First Out(LIFO) No
Turing Machine Infinite tape Yes
Example of Turing machine
Turing machine M = (Q, X, ∑, δ, q0, B, F) with
 Q = {q0, q1, q2, qf}
 X = {a, b}
 ∑ = {1}
 q0 = {q0}
 B = blank symbol
 F = {qf }
δ is given by −
Tape alphabet
symbol
Present State
‘q0’
Present State
‘q1’
Present State ‘q2’
a 1Rq1 1Lq0 1Lqf
b 1Lq2 1Rq1 1Rqf
Here the transition 1Rq1 implies that the write symbol is 1, the tape moves right, and the
next state is q1. Similarly, the transition 1Lq2 implies that the write symbol is 1, the tape
moves left, and the next state is q2.
Time and Space Complexity of a Turing Machine

4. For a Turing machine, the time complexity refers to the measure of the number of times the
tape moves when the machine is initialized for some input symbols and the space
complexity is the number of cells of the tape written.
Time complexity all reasonable functions −
T(n) = O(n log n)
TM's space complexity −
S(n) = O(n)
Universal Turing Machine
The Turing Machine (TM) is the machine level equivalent to a digital computer.
It was suggested by the mathematician Turing in the year 1930 and has become the most
widely used model of computation in computability and complexity theory.
The model consists of an input and output. The input is given in binary format form on to the
machine’s tape and the output consists of the contents of the tape when the machine halts

5. The problem with the Turing machine is that a different machine must be constructed for
every new computation to be performed for every input output relation.
This is the reason the Universal Turing machine was introduced which along with input on
the tape takes the description of a machine M.
The Universal Turing machine can go on then to simulate M on the rest of the content of the
input tape.
A Universal Turing machine can thus simulate any other machine.(computer running other
computer)
The idea of connecting multiple Turing machine gave an idea to Turing −
 Can a Universal machine be created that can ‘simulate’ other machines?
 This machine is called as Universal Turing Machine
This machine would have three bits of information for the machine it is simulating
 A basic description of the machine.
 The contents of machine tape.
 The internal state of the machine.
The Universal machine would simulate the machine by looking at the input on the tape and
the state of the machine.
It would control the machine by changing its state based on the input. This leads to the idea
of a “computer running another computer”.
It would control the machine by changing its state based on the input. This leads to the idea
of a “computer running another computer”.
The schematic diagram of the Universal Turing Machine is as follows −

6. The Church-Turing thesis says that every solvable decision problem can be transformed into
an equivalent Turing machine problem.
It can be explained in two ways, as given below −
 The Church-Turing thesis for decision problems.
 The extended Church-Turing thesis for decision problems.
Let us understand these two ways.

7. The Church-Turing thesis for decision problems
There is some effective procedure to solve any decision problem if and only if there is a
Turing machine which halts for all input strings and solves the problem.
The extended Church-Turing thesis for decision problems
A decision problem Q is said to be partially solvable if and only if there is a Turing machine
which accepts precisely the elements of Q whose answer is yes.
Proof
A proof by the Church-Turing thesis is a shortcut often taken in establishing the existence of
a decision algorithm.
For any decision problem, rather than constructing a Turing machine solution, let us describe
an effective procedure which solves the problem.
The Church-Turing thesis explains that a decision problem Q has a solution if and only if
there is a Turing machine that determines the answer for every q Q. If no such Turing
ϵ
machine exists, the problem is said to be undecidable.