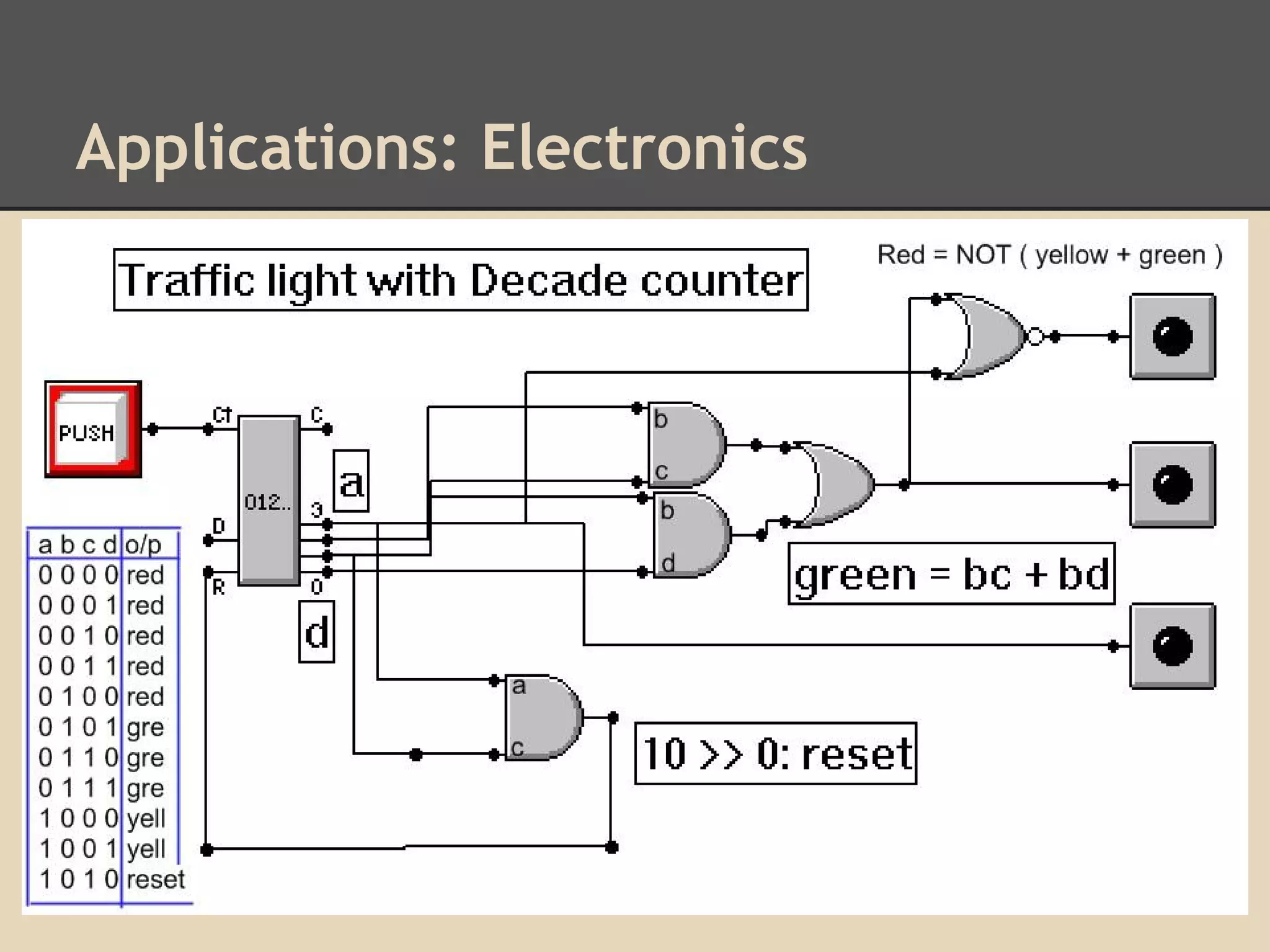
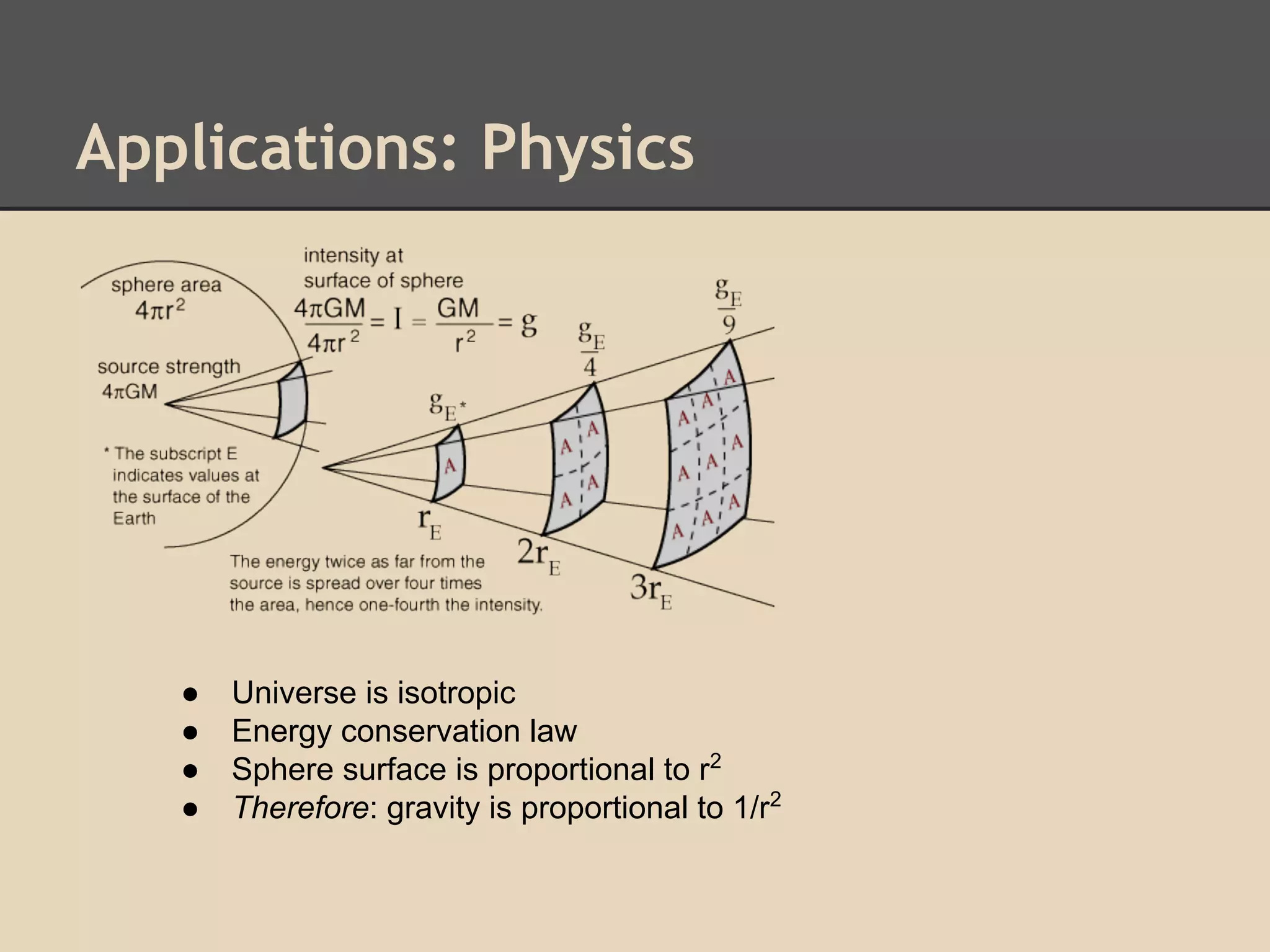
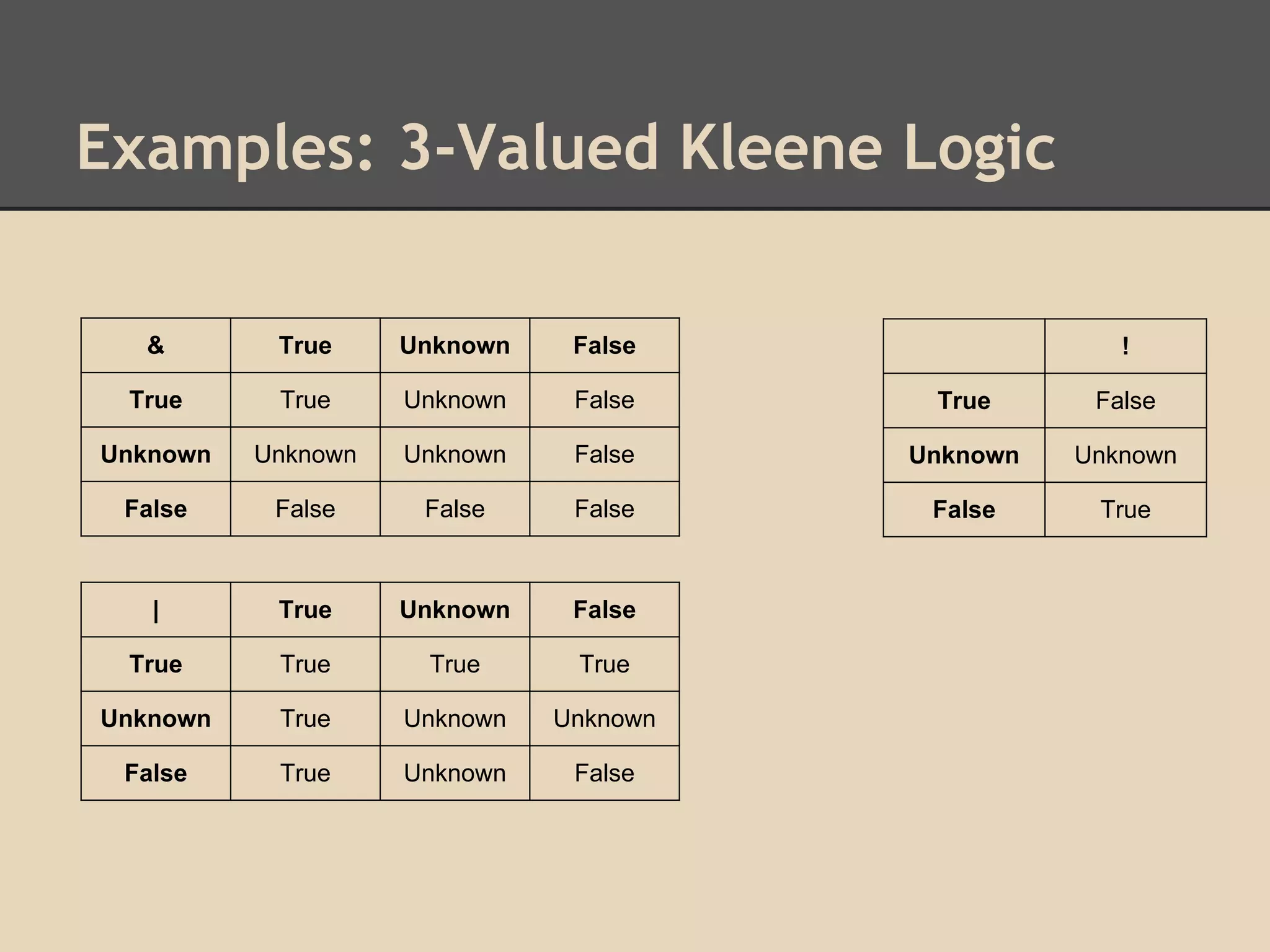
This document provides an overview of logic across different cultures and time periods. It discusses logic in ancient China and India, as well as Greece. It then covers developments in logic in Western Europe between the 19th and 20th centuries. Applications of logic are explored in various domains like law, religion, mathematics, and computer science. Examples are given of different logical systems including Boolean logic, Kleene logic, and Heyting logic. Overall, the document aims to illustrate the diversity of logical interpretations and applications over different eras and civilizations.

1. Truth, Deduction,
Computation
Introduction
Vlad Patryshev
SCU
2013

2. Variety of Interpretations
● different in different cultures
○
○
○
○
China
India
Greece
Modern Europe
● depends on where you apply it
○
○
○
○
○
legal
iq test
math
religion
comp sci

3. Logic in China
Mo Di (墨子) (468-376 BC) and his school
Three tests for the validity of a doctrine: ancient authority, common observation,
and practical effect.
The statement "All statements are mistaken" implies that it is itself mistaken,
and one cannot "reject rejection" without refusing to reject one's own rejection.
"The ghost of a man is not a man," but "The ghost of my brother is my brother."
"A robber is a man, but abounding in robbers is not abounding in men, nor is
being without robbers being without men."
Gōngsūn Lóng (公孫龍) 325–250 BC, School of Names
"One and one cannot become two, since neither becomes two."
“A planet can be any size. A planet can be giant or very small. A dwarf
planet can only be very small. Therefore, one can say that a dwarf planet
is not a planet.”
(But later the only legal logic was Buddhist logic imported from India; later about it)

4. © Copyright 2012 Sanjay Kulkarni

5. Logic in India
● Tetralemma: for a proposition X, there are four
possibilities: X; not X; X and not X; not (X or not X)
● Catuṣkoṭi:
Negative configuration
P
Not (P)
Not-P
Not (Not-P)
Both P and Not-P
Not (Both P and Not-P)
Neither P nor Not-P
dharmacakra (धमच )
Positive configuration
Not (Neither P nor Not-P)

6. India: Navya-Nyaya School
(13th century)
1.Syād-asti — “in some ways it is”
2.Syād-nāsti — “in some ways it is not”
3.Syād-asti-nāsti — “in some ways it is and it is not”
4.Syād-asti-avaktavyaḥ — “in some ways it is and it is
indescribable”
5.Syād-nāsti-avaktavyaḥ — “in some ways it is not and it is
indescribable”
6.Syād-asti-nāsti-avaktavyaḥ — “in some ways it is, it is
not and it is indescribable”
7.Syād-avaktavyaḥ — “in some ways it is indescribable”

7. Logic in India: an Example
Yudhisthira never said a lie, and as a reward,
his chariot that was not touching the earth (a
hovercraft?).
Once Lord Krishna asked him to tell guru
Drona about Ashwathama being killed by
Bhima. Drona’s son’s name was
Ashwathama, but it was an elephant with the
same name that Bhima killed.
Yudhisthra said “Ashwathama was killed, a
man or an elephant”.
Yudhisthira
(यु धि ठर)
The moment Yudhisthira said the lie, though it
was true but not an act of Dharma, his chariot
came down.

8. Logic in Greece
Aristotle (Ἀριστοτέλης) 384–322 BC
Syllogisms
● Every man is a being therefore:
● Every non-being is a non-man
● (which is false because the universal
affirmative has existential import, and
there are no non-beings)
● A chimera is not a man therefore:
● A non-man is not a non-chimera

9. Western Europe, XIX-XX centuries
No matter how correct a mathematical
theorem may appear to be, one ought
never to be satisfied that there was not
something imperfect about it until it also
gives the impression of being beautiful.
“In mathematics the art of asking
questions is more valuable than
solving problems.”
Georg Cantor,
1845-1918
“The essence of mathematics lies in
its freedom.”

10. Europe, XX century
David Hilbert, 1862-1943
Kurt Gödel, 1906-1978
“No one shall expel us
from the paradise that
Cantor has created for
us.”
“The more I think about
language, the more it
amazes me that people ever
understand each other at
all.”
“The brain is a computing
machine connected with a
spirit.”
Paul Cohen,1934–2007
Saul Kripke, b.1940
“Lois Lane believes that
Superman can fly,
although she does not
believe that Clark Kent can
fly.”
“Londres est joli”

11. Applications: Legal
○
○
○
Deductive reasoning:
■ “All people sleep, so students must sleep”
Inductive reasoning:
■ Jane studies every day and is a good student.
■ Tom studies every day and is a good student.
■ Angela studies every day and is a good student.
■ Hence: Good students study every day.
Search for Fallacies:
■ “Example: “The possession of nuclear weapons is a moral
abomination. Even Edward Teller, the ‘father of the hydrogen bomb,’
urged the United States to halt production once the full extent of their
destructive power became known.”
■ Explanation: While it may seem persuasive that even the “father” of
the hydrogen bomb disapproved of its development, note that Teller
was a physicist, not a cleric or moral philosopher. His views on
morality are completely outside his expertise.”

12. Applications: Religion
●
Proofs of God’s existence:
○ Deductive
■
■
■
○
God is the greatest conceivable being.
It is greater to exist than not to exist.
Therefore, God exists.
Karmic: some people in this world are happy, some are in misery therefore, God exists
● Proofs of God’s nonexistence:
○ Deductive
■
○
Can God create a rock so big that He cannot move it?
Inductive
■
A perfect being would have long ago satisfied all its wants and
desires and would no longer be able to take action in the
present without proving that it had been unable to achieve its
wants faster—showing it imperfect.

13. Applications: IQ Tests
○
Correct iq tests
A Division Director scheduled six meetings on Wednesday with his direct reports: Anita, Harold,
Ben, Markus, Sheila, and Carol. Each meeting is with only one direct report, and each direct
report will meet only once with the Division Director. The Division Director labeled the meeting
timeslots in order from 1 through 6, with timeslot 1 occurring first and timeslot 6 occurring last.
Ben's meeting will be immediately after Harold's.
Anita's meeting will be two meetings after Markus'.
Anita's meeting will be before, but not immediately before, Carol's.
Which direct report is in timeslot 2?
Anita? Harold? Ben? Markus? Sheila?
○
Incorrect IQ tests
All cacti are plants; most of the plants are pines; all pines have needles; hence: some cacti have
needles. Is it true?

14. Applications: Common Sense
Paradoxes and Fallacies
○ Contradiction
■
■
The sentence below is true.
The sentence above is false.
○ There is someone in the pub such that, if he is
drinking, everyone in the pub is drinking.
○ "the first number not nameable in under ten words"
○ Pinocchio paradox: What would happen if Pinocchio
said "My nose will be growing"?
(see also: List of Fallacies on wikipedia)

15. Applications: Common Sense
● Misconceptions
○ 2*2=4
○ Every statement is either right or wrong
○ Axioms are true, and this is why theorems that follow
from axioms are also true
○ Every logic is Boolean or can be expressed in
Boolean
○ Boolean logic has only two values
○ Programs only deal with finite entities

16. Applications: Electronics

17. Applications: Physics
●
●
●
●
Universe is isotropic
Energy conservation law
Sphere surface is proportional to r2
Therefore: gravity is proportional to 1/r2

18. Applications: Comp Sci
○ Binary logic (used in circuits) and Ternary (Setun, a
Russian-made computer)
○ Untyped lambda calculus and typed lambda calculus;
Curry-Howard isomorphism
○ Bahrendregdt’s Lambda-cube
In mathematical logic and type theory, the λ-cube is a framework for
exploring the axes of refinement in Coquand's calculus of
constructions, starting from the simply typed lambda calculus as the
vertex of a cube placed at the origin, and the calculus of constructions
(higher order dependently-typed polymorphic lambda calculus) as its
diametrically opposite vertex.
○ Logic programming (e.g. Prolog)
○ Theorems for Free (Girard-Reynolds): e.g.
if f:A×B -> A for all possible A and B,
then f(a,b) == a.

19. Set Theory and SQL
select * from users where age < 18;

20. Examples: Two-valued Boolean Logic
&
True
False
True
True
False
True
False
False
False
False
False
True
|
True
False
True
True
True
False
True
False
!

21. Examples: 8-valued Boolean Logic
!
^
0
1
2
3
4
5
6
7
0
0
0
0
0
0
0
0
0
0
7
1
0
1
0
1
0
1
0
1
1
6
2
0
0
2
2
0
0
2
2
2
5
3
0
1
2
3
0
1
2
3
3
4
4
0
0
0
0
4
4
4
4
4
3
5
0
1
0
1
4
5
4
5
5
2
6
0
0
2
2
4
4
6
6
6
1
7
0
1
2
3
4
5
6
7
7
0

22. Examples: 3-Valued Kleene Logic
&
True
Unknown
False
True
True
Unknown
False
True
False
Unknown
Unknown
Unknown
False
Unknown
Unknown
False
False
False
False
False
True
|
True
Unknown
False
True
True
True
True
Unknown
True
Unknown
Unknown
False
True
Unknown
False
!

23. Examples: 3-Valued Heyting Logic
&
True
Unknown
False
True
True
Unknown
False
True
False
Unknown
Unknown
Unknown
False
Unknown
False
False
False
False
False
False
True
|
True
Unknown
False
True
True
True
True
Unknown
True
Unknown
Unknown
False
True
Unknown
False
!

24. Other Interesting Logics Systems
● Linear logic: $1 and $1 != $1
(see "Physics, Topology, Logic and Computation: A Rosetta Stone")
●
●
●
●
Modal logic
Fuzzy Logic
Temporal logic
Higher order logics

25. The Book
We will use this book.
Take it cum grano salis - it was written
for a different target audience (see
“legal” and “common sense” above.
If you can write code in any
programming language, Basic to Agda,
you are already way ahead than most of
the book’s target audience.

26. More Sources
● Lambda-calculus:
http://www.cse.chalmers.
se/research/group/logic/TypesSS05/Extra/geuvers.pdf
● Introduction to Type Theory:
http://www.cs.ru.
nl/~herman/PUBS/IntroTT-improved.pdf
● Lambda, in Haskell:
http://augustss.blogspot.
ru/2007/10/simpler-easier-in-recent-paper-simply.html