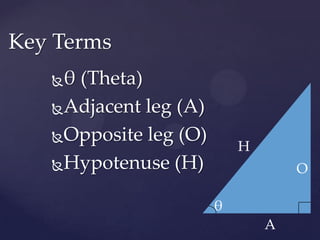
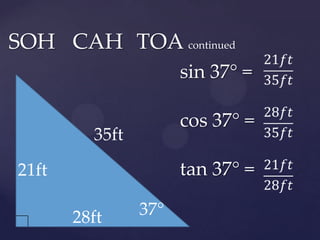
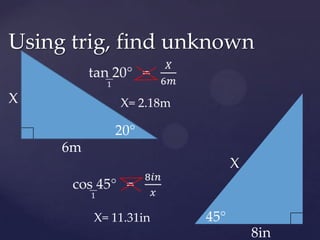
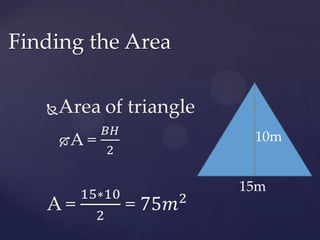
Trigonometry deals with relationships between the sides and angles of triangles. It uses trigonometric functions like sine, cosine, and tangent. Sine relates the opposite side to the hypotenuse, cosine relates the adjacent side to the hypotenuse, and tangent relates the opposite side to the adjacent side. Trigonometry can be used to find unknown side lengths or angles in triangles, including solving "story problems" where trigonometric applications are needed to determine real-world measurements. The document provides examples of using trigonometric functions like sine, cosine, and tangent to solve for unknown values in right and non-right triangles, as well as how to set up and solve word problems involving trigonometric applications.

1. Trigonometry and TrianglesMichael Schmidt

2. TrigonometrySine Cosine TangentLength of triangle legsAngle of triangle cornersArea of trianglesWhat we are doing

3. Branch in MathematicsUses trig functionsTrianglesMostly right trianglesUses relationships to find unknowns Trigonometry

4. θ (Theta)Adjacent leg (A)Opposite leg (O)Hypotenuse (H)Key TermsHOθA

5. SOH: sin θ =𝑂𝑝𝑝𝑜𝑠𝑖𝑡𝑒𝐻𝑦𝑝𝑜𝑡𝑒𝑛𝑢𝑠𝑒CAH: cos θ =𝐴𝑑𝑗𝑎𝑐𝑒𝑛𝑡𝐻𝑦𝑝𝑜𝑡𝑒𝑛𝑢𝑠𝑒TOA: tan θ =𝑂𝑝𝑝𝑜𝑠𝑖𝑡𝑒𝐴𝑑𝑗𝑎𝑐𝑒𝑛𝑡 SOH CAH TOA

6. sin 37° =cos37° =tan 37° =SOH CAH TOA continued21𝑓𝑡35𝑓𝑡28𝑓𝑡35𝑓𝑡21𝑓𝑡28𝑓𝑡 35ft21ft37°28ft

7. What is given?Which trig function? Finding the side length12ftsin 30° = 𝑋12𝑓𝑡 Xsin 30°1 = 𝑋12𝑓𝑡 X= 6ft30°

8. Using trig, find unknowntan 20° = 𝑋6𝑚 1 XX= 2.18m20°6mXcos 45° = 8𝑖𝑛𝑥 1 45°X= 11.31in8in

9. What is known? tan θ = 34Use 𝑡𝑎𝑛−1𝑡𝑎𝑛−1( 34 ) = θθ = 36.86° Using trig to find θ3’θ4’

10. sin θ = 10𝑚15𝑚𝑠𝑖𝑛−1(10𝑚15𝑚 ) = θθ = 41.81° Solve for θθ15m10mcos θ = 7𝑐𝑚9𝑐𝑚𝑐𝑜𝑠−1(7𝑐𝑚9𝑐𝑚 ) = θθ = 38.94° 9cmθ7cm

11. Area of triangleA = 𝐵𝐻2A = 15∗102 = 75𝑚2 Finding the Area10m15m

12. What is given?What is needed?How is it found?tan60 = 𝐵10A =17.32𝑐𝑚∗10𝑐𝑚2 Finding area with trig60°10cmB =17.32cm=86.6𝑐𝑚2

13. GivenNeededsin50 = 𝐻11A= 13∗8.432 Non right trianglesH= 8.43in11inA=54.8𝑖𝑛2 50°13in

14. cos 60 = 𝐻22Pythagorean theorem for the baseA= 19.05∗112 Find area of triangleH=11in60° 22inA=104.78𝑖𝑛2

15. GivenNeededB= X+Ytan 45 = 𝑥16tan 30 = 𝑦16B=25.24cm Find area of triangle continuedHeight = 16cm16cm45°30°XYX=16cmY=9.24cmA=16∗25.242 =201.92𝑐𝑚2

16. A 6ft tall man is standing in front of a light. The light is casting a shadow. If the angle of depression at the man’s head is 60° how long is the shadow?Story Problemstan 60 = 𝐿6 L=10.39ft60°6ftL

17. Story problemsThere is a window 33ft up a building and the only ladder is 40ft long. For safety reasons the ladder is leaned against the building at 52°. Will the ladder reach the window?sin 52 = 𝐻40H=31.52ft 40ftNo, the ladder will not reach the window.52°

18. SOH CAH TOA is keyFind the Given and NeededMake own right triangleDraw a pictureWrap up