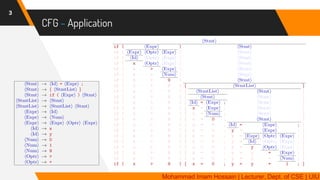
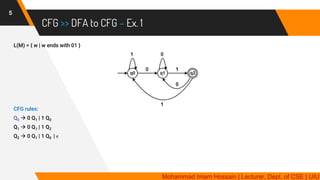
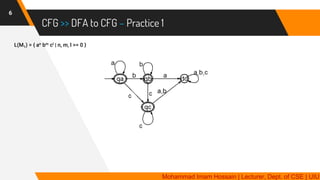
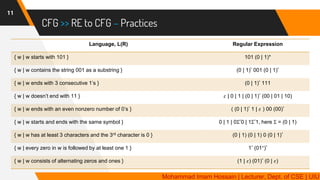
The document provides a comprehensive overview of context-free grammars (CFG) and their relationship with deterministic finite automata (DFA), detailing their components and rules. It includes numerous examples of CFG designs for various languages and regular expressions, along with methods for converting regular expressions to CFG. Additionally, it discusses techniques for creating CFGs that reflect specific language properties like palindromes, linked terminals, and combinations of simpler context-free languages.












![CFG >> Linked Terminals – Practice set 1
17
▸ { 0n 1m | n>m and n, m>=0 } ; let n=m+k then { 0k0m1m | n, m>=0 and k>0 }
S → 0S | 0P
P → 0P1 | ε
▸ { 0n 1m | n=2m and n, m>=0 } = { 02m 1m | m>=0 }
S → 00S1 | ε
▸ { 0x1y 0z | z=x+y and x, y, z >= 0 } = { 0x 1y 0x+y | x, y >= 0 } = { 0x 1y 0y 0x | x, y >= 0 }
S → 0S0 | P
P → 1P0 | ε
▸ All strings of the form 0a 1b 0c where a+c=b [ in short: 0a 1a 1c 0c ]
S → TU
T → 0T1 | ε
U → 1U0 | ε
▸ { 0x1y 0z | z=x-y and x, y, z >= 0 } = { 0z+y 1y 0z | y, z >= 0 } = { 0z 0y 1y 0z | y, z >=0 }
S → 0S0 | P
P → 0P1 | ε
Mohammad Imam Hossain | Lecturer, Dept. of CSE | UIU](https://image.slidesharecdn.com/cfgdesign-201226083834/85/TOC-6-CFG-Design-17-320.jpg)






