Toan pt.de019.2010(+17de)

Thi thử Đại học www.toanpt.net
1
ĐỀ THI THỬ ĐẠI HỌC, CAO ĐẲNG NĂM 2010
Môn thi : TOÁN (ĐỀ 1)
I. PHẦN CHUNG DÀNH CHO TẤT CẢ CÁC THÍ SINH (7,0 điểm)
Câu 1: Cho hàm số
2x 1
y
x 2



.
1) Khảo sát sự biến thiên và vẽ đồ thị (C) của hàm số đã cho.
2) Viết phương trình tiếp tuyến của đồ thị (C),biết hệ số góc của tiếp tuyến bằng 5.
Câu 2:
1) Giải phương trình: 25x
– 6.5x
+ 5 = 0
2) Tính tích phân:
0
I x(1 cos x)dx

  .
3) Tìm giá trị nhỏ nhất và giá trị lớn nhất của hàm số 2
f(x) x ln(1 2x)   trên đoạn [2; 0].
Câu 3:
Cho hình chóp S.ABC có mặt bên SBC là tam giác đều cạnh a, cạnh bên SA vuông góc với mặt
phẳng đáy. Biết góc BAC = 1200
, tính thể tích của khối chóp S.ABC theo a.
Câu 4: Cho x, y, z là các số dương thoả :
1 1 1
1
x y z
   . CMR:
1 1 1
1
2 2 2z y z x y z x y z
  
     
.
II. PHẦN RIÊNG
1. Theo chương trình Chuẩn :
Câu 5a: Trong không gian Oxyz, cho mặt cầu (S) và mặt phẳng (P) có phương trình:
     
2 2 2
(S) : x 1 y 2 z 2 36và(P) : x 2y 2z 18 0          .
1) Xác định tọa độ tâm T và tính bán kính của mặt cầu (S). Tính khoảng cách từ T đến mp(P).
2) Viết p.trình đường thẳng d đi qua T và vuông góc với (P). Tìm tọa độ giao điểm của d và (P).
Câu 6a: Giải phương trình : 8z2
– 4z + 1 = 0 trên tập số phức.
2. Theo chương trình Nâng cao:
Câu 5b: Cho điểm A(1; 2; 3) và đường thẳng d có phương trình
x 1 y 2 z 3
2 1 1
  
 

1) Viết phương trình tổng quát của mặt phẳng đi qua điểm A và vuông góc với đường thẳng d.
2) Tính khoảng cách từ điểm A đến d. Viết phương trình mặt cầu tâm A, tiếp xúc với d.
Câu 6b: Giải phương trình
2
2z iz 1 0   trên tập số phức.

2
A. PHẦN CHUNG CHO TẤT CẢ CÁC THÍ SINH: ( 8 điểm)
Câu 1: ( 2điểm)
Cho hàm số y = 4x3
+ mx2
– 3x
1. Khảo sát và vẽ đồ thị (C) hàm số khi m = 0.
2. Tìm m để hàm số có hai cực trị tại x1 và x2 thỏa x1 = 4x2
Câu 2: (2điểm)
1. Giải hệ phương trình:
2 0
1 4 1 2
x y xy
x y
   

   
2. Giải phương trình: cosx = 8sin3
6
x
 
 
 
Câu 3: (2điểm)
1. Cho hình chóp S.ABC có SA vuông góc với mặt phẳng (ABC), tam giác ABC vuông tại C ;
M,N là hình chiếu của A trên SB, SC. Biết MN cắt BC tại T. Chứng minh rằng tam giác AMN
vuông và AT tiếp xúc với mặt cầu đường kính AB.
2. Tính tích phân A =
2
ln .ln ex
e
e
dx
x x
Câu 4: (2 điểm)
1. Trong không gian với hệ trục tọa độ Oxyz, cho bốn điểm A(4;5;6); B(0;0;1); C(0;2;0);
D(3;0;0). Chứng minh các đường thẳng AB và CD chéo nhau. Viết phương trình đường thẳng
(D) vuông góc với mặt phẳngOxy và cắt được các đường thẳngAB; CD.
2. Cho ba số thực dương a, b, c thỏa:
3 3 3
2 2 2 2 2 2
1
a b c
a ab b b bc c c ca a
  
     
Tìm giá trị lớn nhất của biểu thức S = a + b + c
B. PHẦN TỰ CHỌN: Thí sinh chỉ chọn câu 5a hoặc 5b
Câu 5a: Theo chương trình chuẩn: ( 2 điểm)
1. Trong không gian với hệ trục tọa độ Oxyz, cho điểm A(4;5;6). Viết phương trình mặt phẳng
(P) qua A; cắt các trục tọa độ lần lượt tại I; J; K mà A là trực tâm của tam giác IJK.
2. Biết (D) và (D’) là hai đường thẳng song song. Lấy trên (D) 5 điểm và trên (D’) n điểm và nối
các điểm ta được các tam giác. Tìm n để số tam giác lập được bằng 45.
Câu 5b: Theo chương trình nâng cao: ( 2 điểm)
1. Trong mặt phẳng với hệ trục tọa độ Oxy, cho đường thẳng (D): x – 3y – 4 = 0 và đường tròn
(C): x2
+ y2
– 4y = 0. Tìm M thuộc (D) và N thuộc (C) sao cho chúng đối xứng qua A(3;1).
2. Tìm m để bất phương trình: 52x
– 5x+1
– 2m5x
+ m2
+ 5m > 0 thỏa với mọi số thực x.
Hết

3
Câu I (2 điểm) Cho hàm số 4 2
( ) 2y f x x x  
1. Khảo sát và vẽ đồ thị (C) của hàm số.
2. Trên (C) lấy hai điểm phân biệt A và B có hoành độ lần lượt là a và b. Tìm điều kiện đối
với a và b để hai tiếp tuyến của (C) tại A và B song song với nhau.
Câu II (2 điểm)
1. Giải phương trình lượng giác:
 2 cos sin1
tan cot 2 cot 1
x x
x x x


 
2. Giải bất phương trình:  2
3 1 1
3 3
1
log 5 6 log 2 log 3
2
x x x x     
Câu III (1 điểm) Tính tích phân:  
2
4 4
0
cos 2 sin cosI x x x dx

 
Câu IV (1 điểm) Cho một hình trụ tròn xoay và hình vuông ABCD cạnh a có hai đỉnh liên tiếp A, B
nằm trên đường tròn đáy thứ nhất của hình trụ, hai đỉnh còn lại nằm trên đường tròn đáy thứ hai
của hình trụ. Mặt phẳng (ABCD) tạo với đáy hình trụ góc 450
. Tính diện tích xung quanh và thể
tích của hình trụ.
Câu V (1 điểm) Cho phương trình     341 2 1 2 1x x m x x x x m      
Tìm m để phương trình có một nghiệm duy nhất.
PHẦN RIÊNG (3 điểm): Thí sinh chỉ làm một trong hai phần (Phần 1 hoặc phần 2)
1. Theo chương trình chuẩn.
Câu VI.a (2 điểm)
1. Trong mặt phẳng với hệ tọa độ Oxy, cho đường tròn (C) và đường thẳng  định bởi:
2 2
( ) : 4 2 0; : 2 12 0C x y x y x y        . Tìm điểm M trên  sao cho từ M vẽ được với
(C) hai tiếp tuyến lập với nhau một góc 600
.
2. Trong không gian với hệ tọa độ Oxyz, cho tứ diện ABCD với A(2;1;0), B(1;1;3),
C(2;1;3), D(1;1;0). Tìm tọa độ tâm và bán kính của mặt cầu ngoại tiếp tứ diện ABCD.
Câu VII.a (1 điểm) Có 10 viên bi đỏ có bán kính khác nhau, 5 viên bi xanh có bán kính khác nhau
và 3 viên bi vàng có bán kính khác nhau. Hỏi có bao nhiêu cách chọn ra 9 viên bi có đủ ba màu?
2. Theo chương trình nâng cao.
Câu VI.b (2 điểm)
1. Trong mặt phẳng tọa độ Oxy, cho hình chữ nhật ABCD có diện tích bằng 12, tâm I thuộc
đường thẳng  : 3 0d x y   và có hoành độ
9
2
Ix  , trung điểm của một cạnh là giao điểm của
(d) và trục Ox. Tìm tọa độ các đỉnh của hình chữ nhật.
2. Trong hệ tọa độ Oxyz, cho mặt cầu (S) và mặt phẳng (P) có phương trình là:
2 2 2
( ) : 4 2 6 5 0, ( ) : 2 2 16 0S x y z x y z P x y z           . Điểm M di động trên (S) và điểm N di
động trên (P). Tính độ dài ngắn nhất của đoạn thẳng MN. Xác định vị trí của M, N tương ứng.
Câu VII.b: Cho , ,a b c là những số dương thỏa mãn: 2 2 2
3a b c   . Chứng minh bất đẳng thức
2 2 2
1 1 1 4 4 4
7 7 7a b b c c a a b c
    
     
Hết

4
Câu I (2 điểm) Cho hàm số  3 2
( ) 3 1 1y f x mx mx m x      , m là tham số
1. Khảo sát sự biến thiên và vẽ đồ thị của hàm số trên khi m = 1.
2. Xác định các giá trị của m để hàm số ( )y f x không có cực trị.
Câu II (2 điểm): Giải phương trình :
1).  
4 4
sin cos 1
tan cot
sin 2 2
x x
x x
x

  ; 2).    2 3
4 82
log 1 2 log 4 log 4x x x     
Câu III (1 điểm) Tính tích phân
3
2
2
1
2
1
dx
A
x x



Câu IV (1 điểm) Cho hình nón có đỉnh S, đáy là đường tròn tâm O, SA và SB là hai đường sinh,
biết SO = 3, khoảng cách từ O đến mặt phẳng SAB bằng 1, diện tích tam giác SAB bằng 18. Tính
thể tích và diện tích xung quanh của hình nón đã cho.
Câu V (1 điểm) Tìm m để hệ bất phương trình sau có nghiệm
 
2
2
7 6 0
2 1 3 0
x x
x m x m
  
    



B.PHẦN RIÊNG (3 điểm): Thí sinh chỉ làm một trong hai phần (Phần 1 hoặc phần 2)
1. Cho tam giác ABC biết các cạnh AB, BC lần lượt là 4x + 3y – 4 = 0; x – y – 1 = 0. Phân
giác trong của góc A nằm trên đ.thẳng x + 2y – 6 = 0. Tìm tọa độ các đỉnh của tam giác ABC.
2. Cho hai mặt phẳng   : 2 2z + 5 = 0; Q : 2 2z -13 = 0.P x y x y    Viết phương trình
của mặt cầu (S) đi qua gốc tọa độ O, qua điểm A(5;2;1) và tiếp xúc với cả hai m.phẳng (P) và (Q).
Câu VII.a (1 điểm) Tìm số nguyên dương n thỏa mãn các điều kiện sau:
4 3 2
1 1 2
4 3
1 1
5
4
7
15
n n n
n
n n
C C A
C A
  

 

 

 

(Ở đây ,k k
n n
A C lần lượt là số chỉnh hợp và số tổ hợp chập k của n phần tử)
1. Cho đường thẳng d: x – 5y – 2 = 0 và đường tròn (C):
2 2
2 4 8 0x y x y     .Xác định
tọa độ các giao điểm A, B của đường tròn (C) và đường thẳng d (điểm A có hoành độ dương). Tìm
tọa độ C thuộc đường tròn (C) sao cho tam giác ABC vuông ở B.
2. Cho mặt phẳng (P): 2 2 1 0x y z    và các đường thẳng:
1 2
1 3 5 5
: ; :
2 3 2 6 4 5
x y z x y z
d d
   
   
 
. Tìm các điểm 1 2
d , dM N  sao cho MN // (P) và cách
(P) một khoảng bằng 2.
Câu VII.b: Tính đạo hàm f’(x) của hsố
 3
1
( ) ln
3
f x
x


và giải bpt:
2
0
6
sin
2
'( )
2
t
dt
f x
x






5
Bài 1:
Cho hàm số
4 3 2
x 2x 3 x 1 (1)y x m m     .
1). Khảo sát sự biến thiên và vẽ đồ thị (C) của hàm số (1) khi m = 0.
2). Định m để hàm số (1) có hai cực tiểu.
Bài 2:
1). Giải phương trình: cos3xcos3
x – sin3xsin3
x =
2 3 2
8

2). Giải phương trình: 2x +1 +x  2 2
2 1 2x 3 0x x x     
Bài 3:
Cho các điểm A(1; 1; 0), B(1; 1; 2), C(2; 2; 1), D(1;1;1).
1). Viết phương trình của m.phẳng chứa AB và song song với CD. Tính góc giữa AB, CD.
2). Giả sử mặt phẳng ( ) đi qua D và cắt ba trục tọa độ tại các điểm M, N, P khác gốc O sao
cho D là trực tâm của tam giác MNP. Hãy viết phương trình của ( ).
Bài 4: Tính tích phân:  
2
0
1 sin2xdxI x

  .
Bài 5: Giải phương trình:    1
4 2 2 2 1 sin 2 1 2 0x x x x
y
       .
Bài 6: Giải bất phương trình:
2 2
1 2
9 1 10.3x x x x   
  .
Bài 7:
1). Cho tập A gồm 50 phần tử khác nhau. Xét các tập con không rỗng chứa một số chẵn các
phần tử rút ra từ tập A. Hãy tính xem có bao nhiêu tập con như vậy.
2). Cho số phức
1 3
z
2 2
i   . Hãy tính : 1 + z + z2
.
Bài 8:
Cho lăng trụ ABC.A'B'C' có A'.ABC là h.chóp tam giác đều cạnh đáy AB = a, cạnh bên AA'
= b. Gọi  là góc giữa hai mặt phẳng (ABC) và (A'BC). Tính tan và thể tích của khối chóp
A'.BB'C'C.
Câu 9:
Trong mặt phẳng với hệ toạ độ Oxy cho điểm C(2; 0) và elip (E):
2 2
1
4 1
x y
  .
Tìm toạ độ các điểm A, B thuộc (E), biết rằng hai điểm A, B đối xứng với nhau qua trục hoành và
tam giác ABC là tam giác đều.
Hết

6
PHẦN CHUNG CHO TẤT CẢ CÁC THÍ SINH (7 điểm)
Câu I (2 điểm) Cho hàm số
4 2
( ) 8x 9x 1y f x   
1. Khảo sát sự biến thiên và vẽ đồ thị (C) của hàm số.
2. Dựa vào đồ thị (C) hãy biện luận theo m số nghiệm của phương trình
4 2
8 os 9 os 0c x c x m   với [0; ]x  .
Câu II (2 điểm) : Giải phương trình, hệ phương trình:
1.  
3log
1
2 2
2
x
x x x
 
    
 
; 2.
2 2
2 2
12
12
x y x y
y x y
    

 
Câu III: Tính diện tích của miền phẳng giới hạn bởi các đường
2
| 4 |y x x  và 2y x .
Câu IV (1 điểm) Cho hình chóp cụt tam giác đều ngoại tiếp một hình cầu bán kính r cho trước.
Tính thể tích hình chóp cụt biết rằng cạnh đáy lớn gấp đôi cạnh đáy nhỏ.
Câu V (1 điểm) Định m để phương trình sau có nghiệm
2
4sin3xsinx + 4cos 3x - os x + os 2x + 0
4 4 4
c c m
       
       
     
PHẦN RIÊNG (3 điểm): Thí sinh chỉ làm một trong hai phần (Phần 1 hoặc phần 2)
1. Cho  ABC có đỉnh A(1;2), đường trung tuyến BM: 2 1 0x y   và phân giác trong CD:
1 0x y   . Viết phương trình đường thẳng BC.
2. Cho đường thẳng (D) có phương trình:
2
2
2 2
x t
y t
z t
  

 
  
.Gọi  là đường thẳng qua điểm
A(4;0;1) song song với (D) và I(2;0;2) là hình chiếu vuông góc của A trên (D). Trong các mặt
phẳng qua  , hãy viết phương trình của mặt phẳng có khoảng cách đến (D) là lớn nhất.
Câu VII.a (1 điểm) Cho x, y, z là 3 số thực thuộc (0;1]. Chứng minh rằng
1 1 1 5
1 1 1xy yz zx x y z
  
    
1. Cho hình bình hành ABCD có diện tích bằng 4. Biết A(1;0), B(0;2) và giao điểm I của hai đường
chéo nằm trên đường thẳng y = x. Tìm tọa độ đỉnh C và D.
2. Cho hai điểm A(1;5;0), B(3;3;6) và đường thẳng  có phương trình tham số
1 2
1
2
x t
y t
z t
  

 
 
.Một
điểm M thay đổi trên đường thẳng , tìm điểm M để chu vi tam giác MAB đạt giá trị nhỏ nhất.
Câu VII.b (1 điểm) Cho a, b, c là ba cạnh tam giác. Chứng minh
1 1 2
2
3 3 2 3 3
b c
a
a b a c a b c a c a b
 
     
      
Hết

7
I:PHẦN CHUNG CHO TẤT CẢ CÁC THÍ SINH (7,0 điểm)
CâuI: Cho hàm số 3 2
2 ( 3) 4y x mx m x     có đồ thị là (Cm)
1) Khảo sát sự biến thiên và vẽ đồ thị (C1) của hàm số trên khi m = 1.
2) Cho (d ) có phương trình y = x + 4 và điểm K(1; 3). Tìm các giá trị của tham số m sao cho
(d) cắt (Cm) tại ba điểm phân biệt A(0; 4), B, C sao cho tam giác KBC có diện tích bằng 8 2 .
Câu II:
1) Giải phương trình: cos2 5 2(2 -cos )(sin - cos )x x x x 
2) Giải hệ phương trình:





yyxx
yyxyx
)2)(1(
4)(1
2
2
(x, y  )
CâuIII: 1) Tính tích phân I =
2 2
6
1
sin sin
2
x x dx


 
2) Tìm các giá trị của tham số thực m sao cho phương trình sau có nghiệm thực:
2 2
1 1 1 1
9 ( 2)3 2 1 0x x
m m   
    
Câu IV: Cho hình chóp S. ABC có góc ((SBC), (ACB)) = 600
, ABC và SBC là các tam giác đều cạnh
a. Tính theo a khoảng cách từ B đến mặt phẳng (SAC).
II. PHẦN RIÊNG (3.0 điểm)
C©u V.a: 1. Cho parabol (P): xxy 22
 vµ elip (E): 1
9
2
2
 y
x
. Chøng minh r»ng (P) giao (E)
t¹i 4 ®iÓm ph©n biÖt cïng n»m trªn mét ®êng trßn. ViÕt p.tr×nh ®êng trßn ®i qua 4 ®iÓm ®ã.
2.Cho mÆt cÇu (S) cã ph¬ng tr×nh 011642222
 zyxzyx vµ mÆt ph¼ng () cã
ph¬ng tr×nh 2x + 2y - z + 17 = 0. ViÕt ph¬ng tr×nh mÆt ph¼ng () song song víi () vµ c¾t (S) theo
giao tuyÕn lµ ®êng trßn cã chu vi b»ng 6.
C©u VI.a T×m hÖ sè cña sè h¹ng chøa x2
trong khai triÓn nhÞ thøc Niut¬n cña
n
x
x 





 4
2
1
biÕt r»ng n lµ sè nguyªn d¬ng tháa m·n:
1
6560
1
2
3
2
2
2
2
1
2
3
1
2
0





n
C
n
CCC n
n
n
nnn 
( k
nC lµ sè tæ hîp chËp k cña n phÇn tö)
CâuVb: 1. Cho điểm A(10; 2; 1) và đường thẳng d có phương trình
3
1
12
1 

 zyx
. Lập phương
trình mặt phẳng (P) đi qua A, song song với d và khoảng cách từ d tới (P) là lớn nhất.
2. Cho điểm A(2;–3), B(3;–2),  ABC có diện tích bằng
3
2
; trọng tâm G của  ABC thuộc
đường thẳng (d): 3x – y – 8 = 0. Tìm bán kính đường tròn nội tiếp  ABC.
CâuVIb:
Tìm các số thực b, c để phương trình z2
+ bz + c = 0 nhận số phức z = 1 + i làm một nghiệm.

8
I. PHẦN CHUNG CHO TẤT CẢ THÍ SINH (7,0 điểm)
Câu I (2,0 điểm) Cho hàm số    3 21
y m 1 x mx 3m 2 x
3
     (1)
1. Khảo sát sự biến thiên và vẽ đồ thị hàm số (1) khi m 2
2. Tìm tất cả các giá trị của tham số m để hàm số (1) đồng biến trên tập xác định của nó.
Câu II (2,0 điểm)
1. Giài phương trình:   2cos x 1 sin x cos x 1  
2. Giải phương trình:      
2 3 3
1 1 1
4 4 4
3
log x 2 3 log 4 x log x 6
2
     
Câu III (1,0 điểm) Tính tích phân:
 

2
0
2
6sin5sin
cos

dx
xx
x
I
Câu IV (1,0 điểm) Cho lăng trụ đứng ABC.A'B'C' có đáy là tam giác đều. Mặt phẳng A'BC tạo với
đáy một góc 0
30 và tam giác A'BC có diện tích bằng 8. Tính thể tích khối lăng trụ.
Câu V (1,0 điểm) Cho x, y là hai số dương thỏa điều kiện
5
x y
4
  .
Tìm GTNN của biểu thức:
4 1
S
x 4y
 
II. PHẦN RIÊNG (3 điểm)
Thí sinh chỉ được làm một trong hai phần (phần 1 hoặc 2).
1. Theo chương trình Chuẩn:
Câu VIa (2.0 điểm)
1. Trong mặt phẳng Oxy. Viết phương trình đường thẳng ( ) đi qua điểm M(3;1) và cắt
trục Ox, Oy lần lượt tại B và C sao cho tam giác ABC cân tại A với A(2;2).
2. Cho điểm A(4;0;0) và điểm  0 0 0 0B(x ;y ;0), x 0;y 0  sao cho OB 8 và góc
 0
AOB 60 . Xác định tọa độ điểm C trên trục Oz để thể tích tứ diện OABC bằng 8.
Câu VII.a (1,0 điểm)
Từ các chữ số 0;1;2;3;4;5 có thể lập được bao nhiêu số tự nhiên mà mỗi số có 6 chữ số
khác nhau và chữ số 2 đứng cạnh chữ số 3.
2. Theo chương trình Nâng cao:
Câu VIb (2,0 điểm)
1. Viết phương trình đường thẳng ( ) đi qua điểm M(4;1) và cắt các tia Ox, Oy lần lượt
tại A và B sao cho giá trị của tồng OA OB nhỏ nhất.
2. Cho tứ diện ABCD có ba đỉnh A(2;1; 1),B(3;0;1),C(2; 1;3)  , còn đỉnh D nằm trên
trục Oy. Tìm tọa độ đỉnh D nếu tứ diện có thể tích V 5
Câu VII.b (1,0 điểm)
Từ các số 0;1;2;3;4;5. Hỏi có thể thành lập được bao nhiêu số có 3 chữ số không chia hết
cho 3 mà các chữ số trong mỗi số là khác nhau.
Hết

9
Câu I: (2 điểm) Cho hàm số:  3 2
3 1 9 2y x m x x m      (1) có đồ thị là (Cm)
1) Khảo sát và vẽ đồ thị hàm số (1) với m =1.
2) Xác định m để (Cm) có cực đại, cực tiểu và hai điểm cực đại cực tiểu đối xứng với nhau qua
đường thẳng
1
2
y x .
Câu II: (2,5 điểm)
1) Giải phương trình:
   3
sin 2 cos 3 2 3 os 3 3 os2 8 3 cos sinx 3 3 0x x c x c x x       .
2) Giải bất phương trình :  2
2 1
2
1 1
log 4 5 log
2 7
x x
x
 
    
 
.
3) Tính diện tích hình phẳng giới hạn bởi các đường y=x.sin2x, y=2x, x=
2

.
Câu III: (2 điểm)
1) Cho hình lăng trụ ABC.A’B’C’ có đáy ABC là tam giác đều cạnh a, cạnh bên hợp với đáy
một góc là 450
. Gọi P là trung điểm BC, chân đường vuông góc hạ từ A’ xuống (ABC) là H sao cho
1
2
AP AH
 
. gọi K là trung điểm AA’,   là mặt phẳng chứa HK và song song với BC cắt BB’
và CC’ tại M, N. Tính tỉ số thể tích
' ' '
ABCKMN
A B C KMN
V
V
.
2) Giải hệ phương trình sau trong tập số phức:
 
2
2
2 2 2 2
6
5
6 0
a a
a a
a b ab b a a

   
     
Câu IV: (2,5 điểm)
1) Cho m bông hồng trắng và n bông hồng nhung khác nhau. Tính xác suất để lấy được 5 bông
hồng trong đó có ít nhất 3 bông hồng nhung? Biết m, n là nghiệm của hệ sau:
2 2 1
3
1
9 19
2 2
720
m
m n m
n
C C A
P




  

 
2 ) Cho Elip có phương trình chính tắc
2 2
1
25 9
x y
  (E), viết phương trình đường thẳng song
song Oy và cắt (E) tại hai điểm A, B sao cho AB=4.
3) Cho hai đường thẳng d1 và d2 lần lượt có phương trình:
1
2
: 2
3
x t
d y t
z t
 

 
  
2
1 2 1
:
2 1 5
x y z
d
  
 
Viết phương trình mặt phẳng cách đều hai đường thẳng d1 và d2?
Câu V: Cho a, b, c 0 và 2 2 2
3a b c   . Tìm giá trị nhỏ nhất của biểu thức
3 3 3
2 2 2
1 1 1
a b c
P
b c a
  
  

10
I.PHẦN CHUNG CHO TẤT CẢ THÍ SINH. (7 điểm)
Câu I.(2 điểm)
Cho hàm số y = x3
+ mx + 2 (1)
1. Khảo sát sự biến thiên và vẽ đồ thị của hàm số (1) khi m = 3.
2. Tìm m để đồ thị hàm số (1) cắt trục hòanh tại một điểm duy nhất.
Câu II. (2 điểm)
1. Giải hệ phương trình :






22
1
322
33
yxyyx
yx
2. Giải phương trình: xxx tansin2)
4
(sin2 22


.
Câu III.(1 điểm) Tính tích phân



2
1
2
4
dx
x
x
I
Câu IV.(1 điểm)
Cho hình chóp S.ABCD có đáy ABCD là hình vuông cạnh a, SA = h vuông góc mặt phẳng
(ABCD), M là điểm thay đổi trên CD. Kẻ SH vuông góc BM. Xác định vị trí M để thể tích tứ diện
S.ABH đạt giá trị lớn nhất. Tính giá trị lớn nhất đó.
Câu V.(1 điểm) Tìm m để phương trình sau có nghiệm thực:
mxx 4 2
1
II. PHẦN RIÊNG. (3 điểm)
Thí sinh chỉ được làm một trong hai phần (phần a họăc phần b)
Câu VI a.(2 điểm)
1.Trong hệ tọa độ Oxy, cho hai đường thẳng d1: x – 2y + 3 = 0, d2 : 4x + 3y – 5 = 0. Lập phương
trình đường tròn (C) có tâm I trên d1, tiếp xúc d2 và có bán kính R = 2.
2.Cho hai đường thẳng d1:
211
zyx
 , d2:








tz
ty
tx
1
21
và mặt phẳng (P): x – y – z = 0. Tìm
tọa độ hai điểm M 1d , N 2d sao cho MN song song (P) và MN = 6
Câu VII a.(1 điểm) Tìm số phức z thỏa mãn :
1
4








iz
iz
Câu VI b.(2 điểm)
1. Cho hình chữ nhật ABCD có cạnh AB: x – 2y – 1 = 0, đường chéo BD: x – 7y + 14 = 0 và
đường chéo AC qua điểm M(2 ; 1). Tìm tọa độ các đỉnh của hình chữ nhật.
2. Cho ba điểm O(0 ; 0 ; 0), A(0 ; 0 ; 4), B(2 ; 0 ; 0) và mp(P): 2x + 2y – z + 5 = 0. Lập p.tr
m.cầu (S) đi qua ba điểm O, A, B và có khỏang cách từ tâm I đến mặt phẳng (P) bằng
3
5
.
Câu VII b.(1điểm) Giải bất phương trình: 3log3log
3
xx 

11
CÂU I:
Cho hàm số :
323
m
2
1
mx
2
3
xy 
1/ Khảo sát và vẽ đồ thị hàm số khi m=1.
2/ Xác định m để đồ thị hàm số có cực đại, cực tiểu đối xứng nhau qua đt y = x
CÂU II:
1). Giải phương trình:
2 2 3 3
tan tan .sin cos 1 0x x x   
2). Cho PT:
2
5 1 5 6x x x x m        (1)
a)Tìm m để pt(1)có nghiệm.
b)Giải PT khi  2 1 2m  
CÂU III:
1) Tính tích phân: I=
 
4
3
41
1
dx
x x 
2) Tính các góc của tam giác ABC biết: 2A=3B ;
2
3
a b
CÂU IV:
1).Viết phương trình mặt phẳng (P) qua O , vuông góc với mặt phẳng
(Q) : x + y + z = 0 và cách điểm M(1;2; 1 ) một khoảng bằng 2 .
2). Có 6 học sinh nam và 3học sinh nữ xếp hàng dọc đi vào lớp. Hỏi có bao nhiêu cách xếp để
có đúng 2HS nam đứng xen kẽ 3HS nữ
CÂU V:
1). Cho đường thẳng (d ) :
x 2 4t
y 3 2t
z 3 t
  

 
   
và mặt phẳng (P) : x y 2z 5 0    
Viết phương trình đ.thẳng (  ) nằm trong (P), song song với (d) và cách (d) một khoảng là 14
2). Giải PT:
2 1 1 1
5.3 7.3 1 6.3 9 0x x x x  
    
CÂU VI: Giải hệ pt:
z z z 4 2i
1 2 3
2z z z 2 5i
1 2 3
z 2z 3z 9 2i
1 2 3
    

   

   

12
I.PhÇn chung cho tÊt c¶ thÝ sinh (7 ®iÓm)
C©u I (2 ®iÓm). Cho hµm sè
2
12



x
x
y cã ®å thÞ lµ (C)
1.Kh¶o s¸t sù biÕn thiªn vµ vÏ ®å thÞ cña hµm sè
2.Chøng minh ®êng th¼ng d: y = - x + m lu«n lu«n c¾t ®å thÞ (C) t¹i hai ®iÓm ph©n biÖt A,
B. T×m m ®Ó ®o¹n AB cã ®é dµi nhá nhÊt.
C©u II (2 ®iÓm)
1.Gi¶i ph¬ng tr×nh 9sinx + 6cosx - 3sin2x + cos2x = 8
2.Gi¶i bÊt ph¬ng tr×nh )3(log53loglog 2
4
2
2
2
2  xxx
C©u III (1 ®iÓm). T×m nguyªn hµm 
xx
dx
I 53
cos.sin
C©u IV (1 ®iÓm). Cho l¨ng trô tam gi¸c ABC.A1B1C1 cã tÊt c¶ çc c¹nh b»ng a, gãc t¹o bëi c¹nh bªn
vµ mÆt ph¼ng ®¸y b»ng 300
. H×nh chiÕu H cña ®iÓm A trªn mÆt ph¼ng (A1B1C1) thuéc ®êng th¼ng
B1C1. TÝnh kho¶ng çch gi÷a hai ®êng th¼ng AA1 vµ B1C1 theo a.
C©u V (1 ®iÓm). XÐt ba sè thùc kh«ng ©m a, b, c tháa m·n a2009
+ b2009
+ c2009
= 3. T×m gi¸ trÞ lín nhÊt
cña biÓu thøc P = a4
+ b4
+ c4
II.PhÇn riªng (3 ®iÓm)
1.Theo ch¬ng tr×nh chuÈn
C©u VIa (2 ®iÓm).
1. Cho ®êng trßn (C) cã ph¬ng tr×nh (x-1)2
+ (y+2)2
= 9 vµ ®êng th¼ng d: x + y + m = 0.
T×m m ®Ó trªn ®êng th¼ng d cã duy nhÊt mét ®iÓm A mµ tõ ®ã kÎ ®îc hai tiÕp tuyÕn AB, AC tíi
®êng trßn (C) (B, C lµ hai tiÕp ®iÓm) sao cho tam gi¸c ABC vu«ng.
2. Cho ®iÓm A(10; 2; -1) vµ ®êng th¼ng d cã ph¬ng tr×nh








tz
ty
tx
31
21
. LËp ph¬ng tr×nh
mÆt ph¼ng (P) ®i qua A, song song víi d vµ kho¶ng çch tõ d tíi (P) lµ lín nhÊt.
C©u VIIa (1 ®iÓm). Cã bao nhiªu sè tù nhiªn cã 4 ch÷ sè kh¸c nhau vµ kh¸c 0 mµ trong mçi sè lu«n
lu«n cã mÆt hai ch÷ sè ch½n vµ hai ch÷ sè lÎ.
2.Theo ch¬ng tr×nh n©ng cao (3 ®iÓm)
C©u VIb (2 ®iÓm)
1. Cho ®êng trßn (C): x2
+ y2
- 2x + 4y - 4 = 0 vµ ®êng th¼ng d: x + y + m = 0. T×m m ®Ó
trªn ®êng th¼ng d cã duy nhÊt mét ®iÓm A mµ tõ ®ã kÎ ®îc hai tiÕp tuyÕn AB, AC tíi ®êng trßn
(C) (B, C lµ hai tiÕp ®iÓm) sao cho tam gi¸c ABC vu«ng.
2. Cho ®iÓm A(10; 2; -1) vµ ®êng th¼ng d cã ph¬ng tr×nh
3
1
12
1 

 zyx
. LËp ph¬ng
tr×nh mÆt ph¼ng (P) ®i qua A, song song víi d vµ kho¶ng çch tõ d tíi (P) lµ lín nhÊt.
C©u VIIb (1 ®iÓm)
Cã bao nhiªu sè tù nhiªn cã 5 ch÷ sè kh¸c nhau mµ trong mçi sè lu«n lu«n cã mÆt hai ch÷ sè
ch½n vµ ba ch÷ sè lÎ.

13
I. PHẦN CHUNG: (7 điểm)
Câu 1:Cho haøm soá: y = x3
+ 3x2
+ mx + 1 coù ñoà (Cm); (m laø tham soá).
1. Khaûo saùt söï bieán thieân vaø veõ ñoà thò haøm soá khi m = 3.
2. Xaùc ñònh m ñeå (Cm) caét ñöôøng thaúng y = 1 taïi 3 ñieåm phaân bieät C(0, 1), D, E sao cho caùc
tieáp tuyeán cuûa (Cm) taïi D vaø E vuoâng goùc vôùi nhau.
Câu 2: 1. Giaûi phöông trình: 2cos3x + 3 sinx + cosx = 0
2. Giải hệ phương trình
2 2
2 2
91 2 (1)
91 2 (2)
x y y
y x x
    

   
Câu 3: Cho soá thöïc b  ln2. Tính J =


x
ln10
b 3 x
e dx
e 2
vaø tìm
b ln2
lim J.
Câu 4: Tính theå tích cuûa hình choùp S.ABC, bieát ñaùy ABC laø moät tam giaùc ñeàu caïnh a, maët beân
(SAB) vuoâng goùc vôùi ñaùy, hai maët beân coøn laïi cuøng taïo vôùi ñaùy goùc 90o
.
Câu 5: Ch x, y, z dương thoả
1 1 1
2009
x y z
   . Tìm GTLN của biểu thức
P =
1 1 1
2 2 2x y z x y z x y z
 
     
II.PHẦN TỰ CHỌN:
1.Phần 1: Theo chương trình chuẩn
Câu 6: 1a/
1.Phương trình hai cạnh của một tam giaùc trong mặt phẳng tọa ®é là :5x - 2y + 6 = 0;
4x + 7y – 21 = 0. viết phương trình cạnh thứ ba của tam giac đó, biết rằng trực taâm của no
trung với gốc tọa độ O.
2. Tìm treân Ox ñieåm A caùch ñeàu ñ.thaúng (d) :
2
2z
2
y
1
1x 


vaø mp(P) : 2x – y – 2z = 0.
Câu 6.2a/
Cho taäp hôïp X =  0,1,2,3,4,5,6,7 . Coù theå laäp ñöôïc bao nhieâu soá tự nhiªn goàm 5 chöõ soá
khaùc nhau ñoâi moät töø X, sao cho moät trong ba chöõ soá ñaàu tieân phaûi baèng 1.
2. Phần 2: Theo chương trình naâng cao.
Câu 6b. 1b/
1. Cho đường trßn (C): x2
+ y2
– 6x + 5 = 0. Tìm M thuộc trục tung sao cho qua M kẽ được hai
tiếp tuyến của (C) sao cho goùc giữa hai tiếp tuyến đó bằng 600
.
2. Cho hai ñöôøng thaúng: (d1) :








4z
ty
t2x
; (d2) :
3
0
x t
y t
z
 


 
. CM (d1) vaø (d2) cheùo nhau. Vieát
phöông trình maët caàu (S) coù ñöôøng kính laø ñoaïn vuoâng goùc chung cuûa (d1) vaø (d2).
Câu 6b.2b/ Giaûi phöông trình sau trong C: Z4
– Z3
+ 6Z2
– 8Z – 16 = 0

14
PHẦN CHUNG CHO TẤT CẢ CÁC THÍ SINH
Câu I (2 điểm):
1).Khảo sát và vẽ đồ thị (C) của h.số :
3x 4
y
x 2



. Tìm điểm thuộc (C) cách đều 2 tiệm cận .
2).Tìm các giá trị của m để phương trình sau có 2 nghiệm trên đoạn
2
0;
3
 
  
.
sin6
x + cos6
x = m ( sin4
x + cos4
x )
Câu II (2 điểm):
1).Tìm các nghiệm trên  0;2 của phương trình :
sin3x sin x
sin 2x cos2x
1 cos2x

 

2).Giải phương trình:
3 3x 34 x 3 1   
Câu III (1 điểm): Cho chóp S.ABC có đáy ABC là tam giác vuông tại C, AC = 2, BC = 4. Cạnh
bên SA = 5 vuông góc với đáy. Gọi D là trung điểm cạnh AB.
1).Tính góc giữa AC và SD; 2).Tính khoảng cách giữa BC và SD.
Câu IV (2 điểm): 1).Tính tích phân: I =
2
0
sin x cosx 1
dx
sin x 2cosx 3

 
 
2). a.Giải phương trình sau trên tập số phức C : | z | iz = 1 – 2i
b.Hãy xác định tập hợp các điểm trong mặt phẳng phức biểu diễn các số phức z thoả mãn
1 < | z – 1 | < 2
PHẦN TỰ CHỌN: Thí sinh chọn câu V.a hoặc câu V.b
Câu V.a.( 2 điểm ) Theo chương trình Chuẩn
1).Viết phương trình các cạnh của tam giác ABC biết B(2; 1), đường cao và đường phân giác
trong qua đỉnh A, C lần lượt là : (d1) : 3x – 4y + 27 = 0 và (d2) : x + 2y – 5 = 0
2). Cho các đường thẳng: 1
x 1
d : y 4 2t
z 3 t


  
  
và  2
x 3u
d : y 3 2u
z 2
 

 
  
a. Chứng minh rằng (d1) và (d2) chéo nhau.
b. Viết phương trình mặt cầu (S) có đường kính là đoạn vuông góc chung của (d1) và (d2).
3). Một hộp chứa 30 bi trắng, 7 bi đỏ và 15 bi xanh . Một hộp khác chứa 10 bi trắng, 6 bi đỏ và 9
bi xanh . Lấy ngẫu nhiên từ mỗi hộp bi một viên bi . Tìm xác suất để 2 bi lấy ra cùng màu .
Câu V.b.( 2 điểm ) Theo chương trình Nâng cao
1).Cho tam giác ABC vuông tại A, p.trình đt BC là : 3 x – y 3 = 0, các đỉnh A và B thuộc
Ox và bán kính đ.tròn nội tiếp tam giác ABC bằng 2 . Tìm tọa độ trọng tâm G của tam giác ABC.
2).Cho đ.thẳng (d) :
x t
y 1
z t


 
  
và 2 mp (P) : x + 2y + 2z + 3 = 0 và (Q) : x + 2y + 2z + 7 = 0
a. Viết phương trình hình chiếu của (d) trên (P)
b. Lập ptr mặt cầu có tâm I thuộc đường thẳng (d) và tiếp xúc với hai mặt phẳng (P) và (Q)
3). Chọn ngẫu nhiên 5 con bài trong bộ tú lơ khơ . Tính xác suất sao cho trong 5 quân bài đó có
đúng 3quân bài thuộc 1 bộ ( ví dụ 3 con K )

15
I.PhÇn chung cho tÊt c¶ thÝ sinh (7 ®iÓm)
C©u I (2 ®iÓm). Cho hµm sè
2
12



x
x
y cã ®å thÞ lµ (C)
1.Kh¶o s¸t sù biÕn thiªn vµ vÏ ®å thÞ cña hµm sè
2.Chøng minh ®êng th¼ng: mxy  lu«n lu«n c¾t ®å thÞ (C) t¹i hai ®iÓm ph©n biÖt A,
B. T×m m ®Ó ®o¹n AB cã ®é dµi nhá nhÊt.
C©u II (2 ®iÓm)
1.Gi¶i ph¬ng tr×nh 9sinx + 6cosx - 3sin2x + cos2x = 8
2.Gi¶i bÊt ph¬ng tr×nh )3(log53loglog 2
4
2
2
2
2  xxx
C©u III (1 ®iÓm). T×m nguyªn hµm 
xx
dx
I 53
cos.sin
C©u IV (1 ®iÓm). Cho l¨ng trô tam gi¸c ABC.A1B1C1 cã tÊt c¶ çc c¹nh b»ng a, gãc t¹o bëi c¹nh bªn
vµ mÆt ph¼ng ®¸y b»ng 300
. H×nh chiÕu H cña ®iÓm A trªn mÆt ph¼ng (A1B1C1) thuéc ®êng th¼ng
B1C1. TÝnh kho¶ng çch gi÷a hai ®êng th¼ng AA1 vµ B1C1 theo a.
C©u V (1 ®iÓm). XÐt ba sè thùc kh«ng ©m a, b, c tháa m·n a2009
+ b2009
+ c2009
= 3. T×m gi¸ trÞ lín nhÊt
cña biÓu thøc P = a4
+ b4
+ c4
II.PhÇn riªng (3 ®iÓm)
1.Theo ch¬ng tr×nh chuÈn
C©u Via:
1.Trong mÆt ph¼ng víi hÖ täa ®é Oxy cho ®êng trßn (C) cã ph¬ng tr×nh (x-1)2
+ (y+2)2
= 9
vµ ®êng th¼ng d: x + y + m = 0. T×m m ®Ó trªn ®êng th¼ng d cã duy nhÊt mét ®iÓm A mµ tõ ®ã kÎ
®îc hai tiÕp tuyÕn AB, AC tíi ®êng trßn (C) (B, C lµ hai tiÕp ®iÓm) sao cho tam gi¸c ABC vu«ng.
2.Cho ®iÓm A(10; 2; -1) vµ ®êng th¼ng d cã ph¬ng tr×nh








tz
ty
tx
31
21
. LËp ph¬ng tr×nh
mÆt ph¼ng (P) ®i qua A, song song víi d vµ kho¶ng çch tõ d tíi (P) lµ lín nhÊt.
C©u VIIa: 1). Cã bao nhiªu sè tù nhiªn cã 4 ch÷ sè kh¸c nhau vµ kh¸c 0 mµ trong mçi sè lu«n lu«n
cã mÆt hai ch÷ sè ch½n vµ hai ch÷ sè lÎ.
2) Gi¶i ph¬ng tr×nh: )(,1
4
Cz
iz
iz








2.Theo ch¬ng tr×nh n©ng cao (3 ®iÓm)
C©u VIb (2 ®iÓm)
1.Trong mÆt ph¼ng víi hÖ täa ®é Oxy cho ®êng trßn (C): x2
+ y2
- 2x + 4y - 4 = 0 vµ ®êng
th¼ng d cã ph¬ng tr×nh x + y + m = 0. T×m m ®Ó trªn ®êng th¼ng d cã duy nhÊt mét ®iÓm A mµ
tõ ®ã kÎ ®îc hai tiÕp tuyÕn AB, AC tíi ®êng trßn (C) (B, C lµ hai tiÕp ®iÓm) sao cho tam gi¸c
ABC vu«ng.
2.Cho ®iÓm A(10; 2; -1) vµ ®êng th¼ng d cã ph¬ng tr×nh
3
1
12
1 

 zyx
. LËp ph¬ng
tr×nh mÆt ph¼ng (P) ®i qua A, song song víi d vµ kho¶ng çch tõ d tíi (P) lµ lín nhÊt.
C©u VIIb (1 ®iÓm) Cã bao nhiªu sè tù nhiªn cã 5 ch÷ sè kh¸c nhau mµ trong mçi sè lu«n lu«n cã
mÆt hai ch÷ sè ch½n vµ ba ch÷ sè lÎ.

16
Câu 1. (2,5 điểm).
1. Cho hàm số (C) :
2
2 5
1
x x
y
x
  


a) Khảo sát và vẽ đồ thị hàm số
b) Tìm M  (C) để tổng các khoảng cách từ M đến 2 tiệm cận là nhỏ nhất
2. Từ một điểm bất kì trên đường thẳng x = 2 có thể kẻ được bao nhiêu tiếp tuyến đến đồ thị
(C’) : 196 23
 xxxy
Câu 2. (1,5 điểm)
1. Giải phương trình:   3510325.3 22
 
xx xx






2coscos
2sinsin
yx
yx
Câu 3. (1,5 điểm)
1. Giải phương trình:     02coscoslogsincoslog 1  xxxx
x
x .
2. Giải bất phương trình:     01311 23
 xxxx
3. Có bao nhiêu số tự nhiên gồm 5 chữ số sao cho trong mỗi số các chữ số đứng trước đều lớn
hơn chữ số đứng liền sau nó.
Câu 4. (2 điểm)
1. Trong hệ toạ độ Oxyz cho 2 điểm A(0; 0; 3); B(2, 0, 1) và mp(P):3x – 8y + 7z – 1 = 0
Tìm toạ độ điểm C  (P) sao cho ABC là tam giác đều.
2. Cho tứ diện ABCD có AB = CD = a, AC = BD = b, AD = BC = c. Hãy xác định các góc hợp
bởi các cạnh đối diện của tứ diện đó.
Câu 5. (2,5 điểm).
1. Tính :
/ 4 1
2
3
0 0
sin
; 2 2
cos
x x
I dx J x x x dx
x

    
2. Cho 3 số dương a, b, c. Chứng minh rằng:
2 2 2
1 1 1
.
2
a b c
a bc b ac c ab abc
 
  
  
3. Cho z =
1 3
i
2 2
  , Hãy tính :
1 2 3 2;z;z ;(z) ;1 z z
z
 
(Hết)

17
I. PHẦN CHUNG:
Câu 1:
1. Khảo sát và vẽ đồ thị (C) của hàm số y =
2 4
1
x
x


2. Tìm trên (C) hai điểm đối xứng nhau qua đường thẳng MN biết M( 3;0) và N( 1; 1)
Câu 2:
1. Giải phương trình: 4cos4
x – cos2x
1 3x
os4x +cos
2 4
c =
7
2
2. Giải phương trình: 3x
.2x = 3x
+ 2x + 1
Câu 3:
Tính tích phân: K =
2
0
1 sinx
1+cosx
x
e dx

 
 
 

Câu 4:
Cho hình chóp tam gíac đều S.ABC độ dài cạnh bên bằng 1. Các mặt bên hợp với mặt phẳng
đáy một góc α. Tính thể tích hình cầu nội tiếp hình chóp S.ABC.
Câu 5:
Cho đường thẳng (d):
2 4
3 2 2
x y z 
 

và hai điểm A(1;2; 1), B(7;2;3). Tìm trên (d)
những điểm M sao cho khoảng cách từ đó đến A và B là nhỏ nhất
II. PHẦN RIÊNG:
1) Theo cương trình chuẩn:
Câu 6a:
1.Năm đoạn thẳng có độ dài 2cm, 4cm, 6cm, 8cm, 10cm. Lấy ngẫu nhiên ba đoạn thẳng
trong năm đoạn thẳng trên. Tìm xác suất để ba đoạn thẳng lấy ra lập thành một tam giác.
8
5
x x y x y y
x y
   

 
Câu 7a:
Tìm giá trị nhỏ nhất y = 2
osx
sin (2 osx-sinx)
c
x c
với 0 < x ≤
3

2) Theo chương trình nâng cao:
Câu 6b:
1. Tìm các giá trị x trong khai triển nhị thức Newton:  5lg(10 3 ) ( 2)lg3
2 2
x
n
x 
 biết rằng số
hạng thứ 6 của khai triển bằng 21 và 1 3 2
2n n nC C C 
2. Cho
2 2
3 os in
3 3
c s
 

 
  
 
. Tìm các số phức β sao cho β3
= α
Câu 7b:
Gọi a, b, c là ba cạnh của một tam giác có chu vi bằng 2. Chứng minh rằng:
2 2 252
2 2
27
a b c abc    
Hết

18
Câu I: (2,0 điểm)
Cho hàm số mxxxy  93 23
, trong đó m là tham số thực.
1. Khảo sát sự biến thiên và vẽ đồ thị của hàm số đã cho khi 0m .
2. Tìm tất cả các giá trị của tham số m để đồ thị hàm số đã cho cắt trục hoành tại 3 điểm
phân biệt có hoành độ lập thành cấp số cộng.
Câu II: (2,0 điểm)
1. Giải phương trình:
2
sin
2
1
3
cos
4
1 22 xx
 .
2. Giải phương trình: )4(log3)1(log
4
1
)3(log
2
1
8
8
42
xxx  .
Câu III: (1,0 điểm)
Tính tích phân:  

4
6
2
cos1cos
tan


dx
xx
x
I .
Câu IV: (1,0 điểm)
Tính thể tích của khối hộp ''''. DCBAABCD theo a . Biết rằng ''' DBAA là khối tứ diện đều
cạnh a .
Câu V: ( 1,0 điểm)
Tìm các giá trị của tham số m để phương trình sau có nghiệm duy nhất thuộc đoạn 





 1;
2
1
:
mxxx  12213 232
( Rm ).
Câu VI: (2,0 điểm)
1. Trong mặt phẳng Oxy , cho đường thẳng )(d có phương trình: 052  yx và hai điểm
)2;1(A ; )1;4(B . Viết phương trình đường tròn có tâm thuộc đường thẳng )(d và đi qua hai
điểm A, B .
2. Trong không gian với hệ toạ độ Oxyz , cho hai điểm )2;1;1(A , )2;0;2(B .
a. Tìm quỹ tích các điểm M sao cho 522
 MBMA .
b. Tìm quỹ tích các điểm cách đều hai mặt phẳng )(OAB và )(Oxy .
Câu VII: (1,0 điểm)
1. Với n là số tự nhiên, chứng minh đẳng thức:
113210
2).2().1(.....4.3.2 
 nn
n
n
nnnnn nCnCnCCCC .
x iy 2z 10
x y 2iz 20
ix 3iy (1 i)z 30
  

  
    
……………………. Hết……………………...

19
BÀI GIẢI (ĐỀ 1)
Câu 1:
2) Tieáp tuyeán taïi ñieåm coù hoaønh ñoä x0, coù heä soá goùc baèng –5
 2
0
5
5
( 2)x

 

 x0 = 3 hay x0 = 1 ; y0 (3) = 7, y0 (1) = -3
Phöông trình tieáp tuyeán caàn tìm laø: y – 7 = -5(x – 3) hay y + 3 = -5(x – 1)
 y = -5x + 22 hay y = -5x + 2
Câu 2: 1) 25x
– 6.5x
+ 5 = 0  2
(5 ) 6.5 5 0x x
    5x
= 1 hay 5x
= 5
 x = 0 hay x = 1.
2)
0 0 0
(1 cos ) cosI x x dx xdx x xdx
  
      =
2
0
cos
2
x xdx


 
Ñaët u = x  du = dx; dv = cosxdx, choïn v = sinx
 I =
2
0
0
sin sin
2
x x xdx


   =
2 2
0
cos 2
2 2
x
 
  
3) Ta coù : f’(x) = 2x +
2
2 4x 2x 2
1 2x 1 2x
  

 
f’(x) = 0  x = 1 (loaïi) hay x =
1
2
 (nhaän)
f(-2) = 4 – ln5, f(0) = 0, f(
1
2
 ) =
1
ln 2
4

vì f lieân tuïc treân [-2; 0] neân
[ 2;0]
max f(x) 4 ln5

  vaø
[ 2;0]
1
minf (x) ln2
4
 
Caâu 3: Hình chiếu của SB và SC trên (ABC) là AB và AC , mà SB=SC nên AB=AC
Ta có : BC2
= 2AB2
– 2AB2
cos1200
 a2
= 3AB2
 =
3
a
AB
2
2 2 2
= a SA =
3 3
a a
SA  
2 2
01 1 3 a 3
= . .sin120 = =
2 2 3 2 12
ABC
a
S AB AC
2 3
1 2 3 2
= =
3 12 363
a a a
V (đvtt)
Câu 4.a.:
1) Taâm maët caàu: T (1; 2; 2), baùn kính maët caàu R = 6
d(T, (P)) =
1 4 4 18 27
9
31 4 4
  
 
 
2) (P) coù phaùp vectô (1;2;2)n 

Phöông trình tham soá cuûa ñöôøng thaúng (d) :
1
2 2
2 2
x t
y t
z t
 
 
 
(t  R)
Theá vaøo phöông trình maët phaúng (P) : 9t + 27 = 0  t = -3
 (d)  (P) = A (2; 4; 4)
Caâu 5.a.: 2
8z 4z 1 0   ; / 2
4 4i    ; Căn bậc hai của /
 là 2i
Phương trình có hai nghiệm là
1 1 1 1
z ihayz i
4 4 4 4
   
Caâu 4.b.:
1) (d) coù vectô chæ phöông (2;1; 1)a  

B
A
S
a
a
a
C

20
Phöông trình maët phaúng (P) qua A (1; -2; 3) coù phaùp vectô a

:
2(x – 1) + 1(y + 2) – 1(z – 3) = 0  2x + y – z + 3 = 0
2) Goïi B (-1; 2; -3)  (d)
BA

= (2; -4; 6)
,BA a 
 
 
= (-2; 14; 10)
d(A, (d)) =
, 4 196 100
5 2
4 1 1
BA a
a
      
 
 

Phöông trình maët caàu taâm A (1; -2; 3), baùn kính R = 5 2 :
(x – 1)2
+ (y + 2)2
+ (2 – 3)2
= 50
Câu 5.b.: 2
2z iz 1 0   2
i 8 9     = 9i2
Căn bậc hai của  là 3i
Phương trình có hai nghiệm là
1
z ihayz i
2
   .
BÀI GIẢI TÓM TẮT(ĐỀ 2)
A.PHẦN CHUNG:
Câu 1:
2. TXĐ: D = R
y’ = 12x2
+ 2mx – 3
Ta có: ’ = m2
+ 36 > 0 với mọi m, vậy luôn có cực trị
Ta có:
1 2
1 2
1 2
4
6
1
4
x x
m
x x
x x

  


  


 
9
2
m  
Câu 2:
1.
2 0 (1)
1 4 1 2 (2)
x y xy
x y
   

   
Điều kiện:
1
1
4
x
y




Từ (1) 2 0
x x
y y
     x = 4y
Nghiệm của hệ (2;
1
2
)
2. cosx = 8sin3
6
x
 
 
 
 cosx =  
3
3sinx+cosx
 3 2 2 3
3 3sin 9sin osx +3 3sinxcos os osx = 0x xc x c x c   (3)
Ta thấy cosx = 0 không là nghiêm
(3)  3 2
3 3 tan 8t an x + 3 3 t anx = 0x 
tanx = 0 x = k 
Câu 3:
1.Theo định lý ba đường vuông góc
BC  (SAC)  AN  BC
và AN  SC
AN  (SBC)  AN  MN
Ta có: SA2
= SM.SB = SN.SC
Vây MSN  CSB

21
 TM là đường cao của tam giác STB
 BN là đường cao của tam giác STB
Theo định lý ba đường vuông góc, ta có AB  ST
AB  (SAT) hay AB AT (đpcm)
2.
2 2
(ln )
ln (1 ln ) ln (1 ln )
e e
e e
dx d x
A
x x x x x
 
   =
2
1 1
(ln )
ln 1 ln
e
e
d x
x x
 
 
 

=
2 2
ln(ln ) ln(1 ln )
e e
x x
e e
  = 2ln2 – ln3
Câu 4:
1. +) (4;5;5)BA 

, (3; 2;0)CD  

, (4;3;6)CA 

, (10;15; 23)BA CD    
 
 , . 0BA CD CA   
  
 đpcm
+ Gọi (P) là mặt phẳng qua AB và (P)  (Oxy)  có VTPT 1 ,n BA k   
  
= (5; 4; 0)
 (P): 5x – 4y = 0
+ (Q) là mặt phẳng qua CD và (Q)  (Oxy) có VTPT 1 ,n CD k   
  
= (2; 3; 0)
 (Q): 2x + 3y – 6 = 0
Ta có (D) = (P)(Q)  Phương trình của (D)
2. Ta có:
3
2 2
2
3
a a b
a ab b


 
(1)
 3a3
≥ (2a – b)(a2
+ ab + b2
)
 a3
+ b3
– a2
b – ab2
≥ 0
 (a + b)(a – b)2
 0. (h/n)
Tương tự:
3
2 2
2
3
b b c
b bc c


 
(2) ,
3
2 2
2
3
c c a
c ac a


 
(3)
Cộng vế theo vế của ba bđt (1), (2) và (3) ta được:
3 3 3
2 2 2 2 2 2
3
a b c a b c
a ab b b bc c c ca a
 
  
     
Vậy: S ≤ 3  maxS = 3 khi a = b = c = 1
B. PHẦN TỰ CHỌN:
Câu 5a: Theo chương trình chuẩn
1. Ta có I(a;0;0), J(0;b;0), K(0;0;c) ( ): 1
x y z
P
a b c
   
Ta có
(4 ;5;6), (4;5 ;6)
(0; ; ), ( ;0; )
IA a JA b
JK b c IK a c
   
   
 
 
Ta có:
4 5 6
1
5 6 0
4 6 0
a b c
b c
a c

  

  
  



77
4
77
5
77
6
a
b
c









 ptmp(P)
2.Ta có: n 2 2
5 5 nC C = 45  n2
+ 3n – 18 = 0  n = 3
Câu 5b:
1.M  (D)  M(3b+4;b)  N(2 – 3b;2 – b)
N  (C)  (2 – 3b)2
+ (2 – b)2
– 4(2 – b) = 0  b = 0;b = 6/5
Vậy có hai cặp điểm: M(4;0) và N(2;2) , M’(38/5;6/5) và N’(8/5; 4/5)
2. Đặt X = 5x
 X > 0
Bất phương trình đã cho trở thành: X2
+ (5 + 2m)X + m2
+ 5m > 0 (*)
Bpt đã cho có nghiệm với mọi x khi và chỉ khi (*) có nghiệm với mọi X > 0

22
 < 0 hoặc (*) có hai nghiệm X1 ≤ X2 ≤ 0
Từ đó suy ra m
Đáp án.(ĐỀ 3)
Câ
u
Ý Nội dung Điểm
I 2 1,00
Ta có 3
'( ) 4 4f x x x  . Gọi a, b lần lượt là hoành độ của A và B.
Hệ số góc tiếp tuyến của (C) tại A và B là
3 3
'( ) 4 4 , '( ) 4 4A Bk f a a a k f b b b     
Tiếp tuyến tại A, B lần lượt có phương trình là:
        ' ' ( ) af' ay f a x a f a f a x f a      ;
        ' ' ( ) f' by f b x b f b f b x f b b     
Hai tiếp tuyến của (C) tại A và B song song hoặc trùng nhau khi và chỉ khi:
  3 3 2 2
4a 4a = 4b 4 1 0 (1)A Bk k b a b a ab b         
Vì A và B phân biệt nên a b , do đó (1) tương đương với phương trình:
2 2
1 0 (2)a ab b   
Mặt khác hai tiếp tuyến của (C) tại A và B trùng nhau
       
 
2 2 2 2
4 2 4 2
1 0 1 0
' ' 3 2 3 2
a ab b a ab b
a b
f a af a f b bf b a a b b
         
   
        
,
Giải hệ này ta được nghiệm là (a;b) = (1;1), hoặc (a;b) = (1;1), hai nghiệm này
tương ứng với cùng một cặp điểm trên đồ thị là  1; 1  và  1; 1 .
Vậy điều kiện cần và đủ để hai tiếp tuyến của (C) tại A và B song song với nhau
là
2 2
1 0
1
a ab b
a
a b
    

 
 
II 2,00
1 1,00
Điều kiện:
 cos .sin 2 .sin . tan cot 2 0
cot 1
x x x x x
x
 


0,25
Từ (1) ta có:
 2 cos sin1 cos .sin 2
2 sin
sin cos2 cos cos1
cos sin 2 sin
x x x x
x
x x x x
x x x

  
 
0,25
2sin .cos 2 sinx x x 
 
2
2 4
cos
2
2
4
x k
x k
x k





 
   
   


0,25
Giao với điều kiện, ta được họ nghiệm của phương trình đã cho là
 2
4
x k k

   
0,25
2 1,00
Điều kiện: 3x  0,25

23
Phương trình đã cho tương đương:
     1 1
2
3 3 3
1 1 1
log 5 6 log 2 log 3
2 2 2
x x x x      
     2
3 3 3
1 1 1
log 5 6 log 2 log 3
2 2 2
x x x x       
      3 3 3log 2 3 log 2 log 3x x x x        
0,25
  3 3
2
log 2 3 log
3
x
x x
x
 
         
  
2
2 3
3
x
x x
x

   

2 10
9 1
10
x
x
x
  
    

0,25
Giao với điều kiện, ta được nghiệm của phương trình đã cho là 10x  0,25
III 1,00
1 1,00
 
2
2
0
2
2
0
1
cos2 1 sin 2
2
1 1
1 sin 2 sin 2
2 2
I x x dx
x d x


 
  
 
 
  
 


0,50
   
2 2
2
0 0
32 2
0 0
1 1
sin 2 sin 2 sin 2
2 4
1 1
sin 2 sin 2 0
2 12
| |
d x xd x
x x
 
 
 
  
 
0,50
IV 1,00
Gọi M, N theo thứ tự là trung điểm của AB và
CD. Khi đó OM AB và ' DO N C .
Giả sử I là giao điểm của MN và OO’.
Đặt R = OA và h = OO’. Khi đó:
OMI vuông cân tại O nên:
2 2 2
.
2 2 2 2 2
h a
OM OI IM h a     
0,25
Ta có:
22 2 2 2
2 2 2 2 2 3a
2 4 4 8 8
a a a a
R OA AM MO
  
              
0,25
2 3
2 3a 2 3 2
R . . ,
8 2 16
a a
V h

     0,25
và
2
a 3 2 3
2 Rh=2 . . .
2 22 2
xq
a a
S

   0,25

24
V 1,00
Phương trình     341 2 1 2 1x x m x x x x m       (1)
Điều kiện : 0 1x 
Nếu  0;1x thỏa mãn (1) thì 1 – x cũng thỏa mãn (1) nên để (1) có nghiệm duy
nhất thì cần có điều kiện
1
1
2
x x x    . Thay
1
2
x  vào (1) ta được:
3 01 1
2. 2.
12 2
m
m m
m

    
 
0,25
* Với m = 0; (1) trở thành:
 
2
4 4 1
1 0
2
x x x    
Phương trình có nghiệm duy nhất.
0,25
* Với m = 1; (1) trở thành
   
     
   
4
4
2 2
4 4
1 2 1 2 1 1
1 2 1 1 2 1 0
1 1 0
x x x x x x
x x x x x x x x
x x x x
       
          
      
+ Với 4 4 1
1 0
2
x x x    
+ Với
1
1 0
2
x x x    
Trường hợp này, (1) cũng có nghiệm duy nhất.
0,25
* Với m = 1 thì (1) trở thành:
       
2 2
4 441 2 1 1 2 1 1 1x x x x x x x x x x            
Ta thấy phương trình (1) có 2 nghiệm
1
0,
2
x x  nên trong trường hợp này (1)
không có nghiệm duy nhất.
Vậy phương trình có nghiệm duy nhất khi m = 0 và m = 1.
0,25
VIa 2,00
1 1,00
Đường tròn (C) có tâm I(2;1) và bán kính 5R  .
Gọi A, B là hai tiếp điểm của (C) với hai tiếp của (C) kẻ từ M. Nếu hai tiếp tuyến
này lập với nhau một góc 600
thì IAM là nửa tam giác đều suy ra 2R=2 5IM  .
Như thế điểm M nằm trên đường tròn (T) có phương trình:
   
2 2
2 1 20x y    .
0,25
Mặt khác, điểm M nằm trên đường thẳng , nên tọa độ của M nghiệm đúng hệ
phương trình:
   
2 2
2 1 20 (1)
2 12 0 (2)
x y
x y
    

  
0,25
Khử x giữa (1) và (2) ta được:
   
2 2 2
3
2 10 1 20 5 42 81 0 27
5
x
y y y y
x

         
 

0,25
Vậy có hai điểm thỏa mãn đề bài là:
9
3;
2
M
 
 
 
hoặc
27 33
;
5 10
M
 
 
 
0,25

25
2 1,00
Ta tính được 10, 13, 5AB CD AC BD AD BC      . 0,25
Vậy tứ diện ABCD có các cặp cạnh đối đôi một bằng nhau. Từ đó ABCD là một
tứ diện gần đều. Do đó tâm của mặt cầu ngoại tiếp của tứ diện là trọng tâm G
của tứ diện này.
0,25
Vậy mặt cầu ngoại tiếp tứ diện ABCD có tâm là
3 3
;0;
2 2
G
 
 
 
, bán kính là
14
2
R GA  .
0,50
VII
a
1,00
Số cách chọn 9 viên bi tùy ý là : 9
18C . 0,25
Những trường hợp không có đủ ba viên bi khác màu là:
+ Không có bi đỏ: Khả năng này không xảy ra vì tổng các viên bi xanh và vàng
chỉ là 8.
+ Không có bi xanh: có 9
13C cách.
+ Không có bi vàng: có 9
15C cách.
0,25
Mặt khác trong các cách chọn không có bi xanh, không có bi vàng thì có 9
10C
cách chọn 9 viên bi đỏ được tính hai lần.
Vậy số cách chọn 9 viên bi có đủ cả ba màu là: 9 9 9 9
10 18 13 15 42910C C C C    cách.
0,50
VI
b
2,00
1 1,00
I có hoành độ
9
2
Ix  và  
9 3
: 3 0 ;
2 2
I d x y I
 
      
 
Vai trò A, B, C, D là như nhau nên trung điểm M của cạnh AD là giao điểm của
(d) và Ox, suy ra M(3;0)
   
2 2 9 9
2 2 2 3 2
4 4
I M I MAB IM x x y y       
D
12
. D = 12 AD = 2 2.
3 2
ABCD
ABC
S
S AB A
AB
   
 AD d
M AD



, suy ra phương trình AD:    1. 3 1. 0 0 3 0x y x y        .
Lại có MA = MD = 2 .
Vậy tọa độ A, D là nghiệm của hệ phương trình:
       
2 2 22 22
3 0 3 3
3 2 3 3 23 2
x y y x y x
x y x xx y
           
   
            
3 2
3 1 1
y x x
x y
   
  
    
hoặc
4
1
x
y


 
.Vậy A(2;1), D(4;1),
0,50
9 3
;
2 2
I
 
 
 
là trung điểm của AC, suy ra:
2 9 2 72
2 3 1 2
2
A C
I
C I A
A C C I A
I
x x
x
x x x
y y y y y
y

     
 
      

Tương tự I cũng là trung điểm BD nên ta có: B(5;4).
Vậy tọa độ các đỉnh của hình chữ nhật là (2;1), (5;4), (7;2), (4;1).
0,50
2 1,00

26
Mặt cầu (S) tâm I(2;1;3) và có bán kính R = 3.
Khoảng cách từ I đến mặt phẳng (P):
  
 2.2 2. 1 3 16
, 5
3
d d I P d R
   
     .
Do đó (P) và (S) không có điểm chung.Do vậy, min MN = d –R = 5 3 = 2.
0,25
Trong trường hợp này, M ở vị trí M0 và N ở vị trí N0. Dễ thấy N0 là hình chiếu
vuông góc của I trên mặt phẳng (P) và M0 là giao điểm của đoạn thẳng IN0 với
mặt cầu (S).
Gọi  là đường thẳng đi qua điểm I và vuông góc với (P), thì N0 là giao điểm của
 và (P).
Đường thẳng  có vectơ chỉ phương là  2;2; 1Pn  

và qua I nên có phương
trình là  
2 2
1 2
3
x t
y t t
z t
 

   
  
 .
0,25
Tọa độ của N0 ứng với t nghiệm đúng phương trình:
     
15 5
2 2 2 2 1 2 3 16 0 9 15 0
9 3
t t t t t               
Suy ra 0
4 13 14
; ;
3 3 3
N
 
  
 
.
0,25
Ta có 0 0
3
.
5
IM IN
 
Suy ra M0(0;3;4) 0,25
VII
b
1,00
Áp dụng bất đẳng thức
1 1 4
( 0, 0)x y
x y x y
   

Ta có:
1 1 4 1 1 4 1 1 4
; ;
2 2 2a+b+ca b b c a b c b c c a a b c c a a b
     
         
0,50
Ta lại có:
     
2 2 2
2 2 2 2
2 2 2
1 2 2
2 4 4 2 2 0
2 2 4 7
2 1 1 1 0
a b c a b c
a b c a b c a
a b c
         
     
      
Tương tự: 2 2
1 2 1 2
;
2 7 2 7b c a b c a b c
 
     
Từ đó suy ra 2 2 2
1 1 1 4 4 4
7 7 7a b b c c a a b c
    
     
Đẳng thức xảy ra khi và chỉ khi a = b = c = 1.
0,50
Đáp án(ĐỀ 4)
Câu Ý Nội dung Điểm
2 1,00
+ Khi m = 0 1y x   , nên hàm số không có cực trị. 0,25
+ Khi 0m   2
' 3 6 1y mx mx m    
Hàm số không có cực trị khi và chỉ khi ' 0y  không có nghiệm hoặc có nghiệm
kép
0,50

27
 2 2
' 9 3 1 12 3 0m m m m m       
1
0
4
m  
0,25
1 1,00
 
4 4
sin cos 1
tan cot
sin 2 2
x x
x x
x

  (1)
Điều kiện: sin 2 0x 
0,25
21
1 sin 2
1 sin cos2(1)
sin 2 2 cos sin
x
x x
x x x

 
   
 
0,25
2
2
1
1 sin 2
1 12 1 sin 2 1 sin 2 0
sin 2 sin 2 2
x
x x
x x

      
Vậy phương trình đã cho vô nghiệm.
0,50
2 1,00
   
2 3
4 82
log 1 2 log 4 log 4x x x      (2)
Điều kiện:
1 0
4 4
4 0
1
4 0
x
x
x
x
x
 
  
   
   
0,25
     
 
2
2 2 2 2 2
2 2
2 2
(2) log 1 2 log 4 log 4 log 1 2 log 16
log 4 1 log 16 4 1 16
x x x x x
x x x x
           
       
0,25
+ Với 1 4x   ta có phương trình 2
4 12 0 (3)x x   ;
 
2
(3)
6
x
x

 
  lo¹i
0,25
+ Với 4 1x    ta có phương trình 2
4 20 0x x   (4);
 
 
2 24
4
2 24
x
x
  
 
  lo¹i
Vậy phương trình đã cho có hai nghiệm là 2x  hoặc  2 1 6x  
0,25
III 1,00
Đặt 2 2 2
2
1 1 2 2
dx tdt
t x t x tdt xdx
x x
          
2 2
1 1
dx tdt tdt
x t t
   
 
+ Đổi cận:
1 3
2 2
3 1
2 2
x t
x t
  
  
0,50

28
1 3
32 2
2
12 2
1 23
22
1 1 1 7 4 3
ln ln
1 1 2 1 2 3
|
dt dt t
A
t t t
  
          
  0,50
IV 1,00
Gọi E là trung điểm của AB, ta có:
,OE AB SE AB  , suy ra  SOE AB .
Dựng  OH SE OH SAB   , vậy OH là khoảng
cách từ O đến (SAB), theo giả thiết thì OH = 1.
Tam giác SOE vuông tại O, OH là đường cao, ta có:
2 2 2 2 2 2
2
1 1 1 1 1 1 1 8
1
9 9
9 3
8 2 2
OH SO OE OE OH SO
OE OE
       
   
2 2 2 9 81 9
9
8 8 2 2
SE OE SO SE      
0,25
21 36
. 8 2
92
2 2
SAB
SAB
S
S AB SE AB
SE
    
 
2
2
2 2 2 21 9 9 265
4 2 32
2 8 8 8
OA AE OE AB OE
 
         
 
0,25
Thể tích hình nón đã cho: 21 1 265 265
. . .3
3 3 8 8
V OA SO     0,25
Diện tích xung quanh của hình nón đã cho:
2 2 2 265 337 337
9
8 8 8
265 337 89305
. . .
8 8 8
xq
SA SO OA SA
S OA SA  
      
  
0,25
V 1,00
Hệ bất phương trình
 
2
2
7 6 0 (1)
2 1 3 0 (2)
x x
x m x m
   

    
 1 1 6x   . Hệ đã cho có nghiệm khi và chỉ khi tồn tại  0 1;6x  thỏa mãn
(2).
0,25
   
 
 
2
2 2 3
2 2 3 2 1 ( 1;6 2 1 0)
2 1
x x
x x x m m do x x
x
 
          

Gọi  
2
2 3
( ) ; 1;6
2 1
x x
f x x
x
 
 

0,25
Hệ đã cho có nghiệm  0 01;6 : ( )x f x m   
 
 
 
 
22
2 2
2 42 2 8
'
2 1 2 1
x xx x
f x
x x
  
 
 
;   2 1 17
' 0 4 0
2
f x x x x
 
      
Vì  1;6x nên chỉ nhận
1 17
2
x
 

0,25

29
Ta có:
2 27 1 17 3 17
(1) , (6) ,
3 13 2 2
f f f
    
    
 
Vì f liên tục và có đạo hàm trên [1;6] nên
27
max ( )
13
f x 
Do đó    0 0
1;6
27
1;6 : ( ) max ( )
13x
x f x m f x m m

      
0,25
VIa 2,00
1 1,00
Tọa độ của A nghiệm đúng hệ phương
trình:  
4 3 4 0 2
2;4
2 6 0 4
x y x
A
x y y
     
   
    
0,25
Tọa độ của B nghiệm đúng hệ phương trình  
4 3 4 0 1
1;0
1 0 0
x y x
B
x y y
    
  
    
0,25
Đường thẳng AC đi qua điểm A(2;4) nên phương trình có dạng:
   2 4 0 2 4 0a x b y ax by a b        
Gọi 1 2 3:4 3 4 0; : 2 6 0; : 2 4 0x y x y ax by a b            
Từ giả thiết suy ra    
2 3 1 2; ;     . Do đó
   
 
2 3 1 2 2 2
2 2
|1. 2. | | 4.1 2.3|
cos ; cos ;
25. 55.
0
| 2 | 2 3 4 0
3 4 0
a b
a b
a
a b a b a a b
a b
 
      


          
+ a = 0 0b  . Do đó 3 : 4 0y  
+ 3a – 4b = 0: Có thể cho a = 4 thì b = 3. Suy ra 3 : 4 3 4 0x y    (trùng với
1 ).
Do vậy, phương trình của đường thẳng AC là y 4 = 0.
0,25
Tọa độ của C nghiệm đúng hệ phương trình:  
4 0 5
5;4
1 0 4
y x
C
x y y
   
  
    
0,25
2 1,00
Gọi I(a;b;c) là tâm và R là bán kính của mặt cầu (S). Từ giả thiết ta có:
        
     
, , ,
, ,
OI AI
OI AI d I P d I Q OI d I P
d I P d I Q
 

    


0,25
Ta có:
     
2 2 22 2 2 2 2
5 2 1
10 4 2 30 (1)
OI AI OI AI a b c a b c
a b c
           
   
     2 2 2 2 2 2| 2 2 5|
, 9 2 2 5 (2)
3
a b c
OI d I P a b c a b c a b c
  
           
      | 2 2 5| | 2 2 13|
, ,
3 3
2 2 5 2 2 13 ( )
2 2 4 (3)
2 2 5 2 2 13
a b c a b c
d I P d I Q
a b c a b c
a b c
a b c a b c
     
  
      
            
lo¹i
0,25

30
Từ (1) và (3) suy ra:
17 11 11 4a
; (4)
3 6 3
a
b c

  
Từ (2) và (3) suy ra: 2 2 2
9 (5)a b c  
Thế (4) vào (5) và thu gọn ta được:   2 221 658 0a a  
Như vậy 2a  hoặc
658
221
a  .Suy ra: I(2;2;1) và R = 3 hoặc
658 46 67
; ;
221 221 221
I
 
 
 
và R = 3.
0,25
Vậy có hai mặt cầu thỏa mãn yêu cầu với phương trình lần lượt là:
     
2 2 2
2 2 1 9x y z      và
2 2 2
658 46 67
9
221 221 221
x y z
     
          
     
0,25
VIIa 1,00
Điều kiện: 1 4 5n n   
Hệ điều kiện ban đầu tương đương:
        
  
     
   
1 2 3 4 1 2 3 5
2 3
4.3.2.1 3.2.1 4
1 1 2 3 7
1 1
5.4.3.2.1 15
n n n n n n n
n n
n n n n n
n n n
      
   
 
      

0,50
2
2
9 22 0
5 50 0 10
5
n n
n n n
n
   

     
 

0,50
VIb 2,00
1 1,00
Tọa độ giao điểm A, B là nghiệm của hệ phương trình
2 2
0; 22 4 8 0
1; 35 2 0
y xx y x y
y xx y
       
 
      
0,50
Vì A có hoành độ dương nên ta được A(2;0), B(3;1).
Vì  0
90ABC  nên AC là đường kính đường tròn, tức là điểm C đối xứng với
điểm A qua tâm I của đường tròn. Tâm I(1;2), suy ra C(4;4).
0,50
2 1,00
Phương trình tham số của d1 là:
1 2
3 3
2
x t
y t
z t
 

 
 
. M thuộc d1 nên tọa độ của M
 1 2 ;3 3 ;2t t t  .
Theo đề:
  
 
 
1 222 2
|1 2 2 3 3 4 1| |12 6 |
, 2 2 12 6 6 1, 0.
31 2 2
t t t t
d M P t t t
     
          
  
0,25
+ Với t1 = 1 ta được  1 3;0;2M ;
+ Với t2 = 0 ta được  2 1;3;0M
0,25
+ Ứng với M1, điểm N1 2d cần tìm phải là giao của d2 với mp qua M1 và // mp
(P), gọi mp này là (Q1). PT (Q1) là:
   3 2 2 2 0 2 2 7 0 (1)x y z x y z          .
0,25

31
Phương trình tham số của d2 là:
5 6
4
5 5
x t
y t
z t
 


   
(2)
Thay (2) vào (1), ta được: 12t – 12 = 0  t = 1. Điểm N1 cần tìm là N1(1;
4;0).
+ Ứng với M2, tương tự tìm được N2(5;0;5). 0,25
VIIb 1,00
Điều kiện
 
3
1
0 3
3
x
x
  

 
   3
1
( ) ln ln1 3ln 3 3ln 3
3
f x x x
x
      

;
 
 
1 3
'( ) 3 3 '
3 3
f x x
x x
   
 
0,25
Ta có:
     2
0
0 0
6 6 1 cos 3 3
sin sin sin 0 sin 0 3
2 2
|
t t
dt dt t t
 

 
   

          
0,25
Khi đó:
2
0
6
sin
2
'( )
2
t
dt
f x
x





  
2 13 3 20
3 23 2 1
3
3; 2 3; 2 2
x x
x xx x
x
x x x x
          
          
0,50
HƯỚNG DẪN GIẢI (đề 5)
Bài 1:
2) 4 3 2
x 2x 2 x 1y x m m     (1)
Đạo hàm / 3 2 2
y 4x 3mx 4x 3m (x 1)[4x (4 3m)x 3m]        
 /
2
x 1
y 0
4x (4 3m)x 3m 0 (2)

  
   
 Hàm số có 2 cực tiểu  y có 3 cực trị  y/
= 0 có 3 nghiệm phân biệt
 (2) có 2 nghiệm phân biệt khác 1
2
(3m 4) 0 4
m .
34 4 3m 3m 0
   
   
   
Giả sử: Với
4
m
3
  , thì y/
= 0 có 3 nghiệm phân biệt 1 2 3x , x , x
 Bảng biến thiên:
x  x1 x2 x3 +
y/
0 + 0 0 +
y +
CT
CĐ
CT
+
 Từ bảng biến thiên ta thấy hàm số có 2 cực tiểu.
Kết luận: Vậy, hàm số có 2 cực tiểu khi
4
m .
3
 
Bài 2:
1). Ta có: cos3xcos3
x – sin3xsin3
x =
2 3 2
8

 cos3x(cos3x + 3cosx) – sin3x(3sinx – sin3x) =
2 3 2
8


32
  2 2 2 3 2
os 3x sin 3x+3 os3x osx sin3xsinx
2
c c c

   
2
os4x ,
2 16 2
c x k k Z
 
      .
2) Giải phương trình : 2x +1 +x  2 2
2 1 2x 3 0x x x      . (a)
* Đặt:
          
     
         
2 2
2 2 2
2 2
2 2 22
v u 2x 1
u x 2, u 0 u x 2
v u 1
v x 2x 3 xv x 2x 3, v 0
2
 Ta có:
            
                          
       
  
   
                      
2 2 2 2 2 2 2 2
2 2 2 2v u 1 v u 1 v u u v u v
(a) v u .u 1 .v 0 v u .u .v 0
2 2 2 2 2 2
v u 0 (b)
v u 1
(v u) (v u) 1 0 v u 1
(v u) 1 0 (c)2 2
2 2
 Vì u > 0, v > 0, nên (c) vô nghiệm.
 Do đó:
                 2 2 2 2 1
(a) v u 0 v u x 2x 3 x 2 x 2x 3 x 2 x
2
Kết luận, phương trình có nghiệm duy nhất: x =
1
2
 .
Bài 3:
1) + Ta có
 
 
 
2;0;2
, D 6; 6;6
D 3;3;0
AB
AB C
C
         

 
 . Do đó mặt phẳng (P) chứa AB và song song
CD có một VTPT  1;1; 1n  

và A(1; 1; 0) thuộc (P) có phương trình: x + y – z + 2 = 0.(P)
Thử tọa độ C(2; 2; 1) vào phương trình (P)  C không thuộc (P), do đó (P) // CD.
+       0
. D 1
os , D os , D , D 60
. D 2
AB C
c AB C c AB C AB C
AB C
    
 
 
2) Theo giả thiết ta có M(m; 0; 0) Ox , N(0; n; 0) Oy , P(0; 0; p)  Oz.
Ta có :
   
   
1; 1; 1 ; ; ;0 .
1; 1; 1 ; ;0; .
DP p NM m n DP NM m n
DN n PM m p DN PM m p
        
 
       
   
    .
Mặt khác:
Phương trình mặt phẳng ( ) theo đoạn chắn: 1
x y z
m n p
   . Vì D ( ) nên:
1 1 1
1
m n p

   .
D là trực tâm của MNP 
. 0
. 0
DP NM DP NM
DN PM DN PM
   
 
   
   
    . Ta có hệ:
0
3
0
3
1 1 1
1
m n
m
m p
n p
m n p

  
  
   
 
   

.
Kết luận, phương trình của mặt phẳng ( ): 1
3 3 3
x y z
  

.

33
Bài 4: Tính tích phân  
2
0
1 sin2xdxI x

  . Đặt
x
1
1
sin 2xdx os2x
2
du d
u x
dv v c

  
 
  
I =  
/2
2 2
0 00
1 1 1
1 os2x os2xdx 1 sin 2x 1
2 2 4 4 4
x c c
 

 
        .
Bài 5: Giải phương trình    1
4 2 2 2 1 sin 2 1 2 0x x x x
y
       (*)
Ta có: (*)      
 
 
2
2
2 1 sin 2 1 0(1)
2 1 sin 2 1 os 2 1 0
os 2 1 0(2)
x x
x x x
x
y
y c y
c y
     
         
  
Từ (2)   sin 2 1 1x
y    .
Khi  sin 2 1 1x
y   , thay vào (1), ta được: 2x
= 0 (VN)
Khi  sin 2 1 1x
y    , thay vào (1), ta được: 2x
= 2  x = 1.
Thay x = 1 vào (1)  sin(y +1) = 1  1 ,
2
y k k Z

     .
Kết luận: Phương trình có nghiệm: 1; 1 ,
2
k k Z


 
    
 
.
Bài 6: Giải bất phương trình:
2 2
1 2
9 1 10.3x x x x   
  . Đặt
2
3x x
t 
 , t > 0.
Bất phương trình trở thành: t2
– 10t + 9  0  ( t  1 hoặc t  9)
Khi t  1 
2
2
3 1 0 1 0x x
t x x x
         .(i)
Khi t  9 
2
2 2
3 9 2 0
1
x x x
t x x
x
  
        
(2i)
Kết hợp (i) và (2i) ta có tập nghiệm của bpt là: S = ( ; 2][1;0][1; + ).
Bài 7:
1) Số tập con k phần tử được trích ra từ tập A là 50
k
C  Số tất cả các tập con không rỗng
chứa một số chẵn các phần tử từ A là : S = 2 4 6 50
50 50 50 50S ...C C C C     .
Xét f(x) =  
50 0 1 2 2 49 49 50 50
50 50 50 50 501 ...x C C x C x C x C x      
Khi đó f(1) =250 0 1 2 49 50
50 50 50 50 50...C C C C C      .
f(1) = 0 0 1 2 49 50
50 50 50 50 50...C C C C C     
Do đó: f(1) + f(1) = 250
  2 4 6 50 50
50 50 50 502 ... 2C C C C        50 49
2 1 2 2 1S S     .
Kết luận:Số tập con tìm được là 49
2 1S  
2) Ta có 2 1 3 3
4 4 2
z i   . Do đó: 2 1 3 1 3
1 1 0
2 2 2 2
z z i i
   
            
   
Bài 8: Gọi E là trung điểm của BC, H là trọng tâm của  ABC. Vì A'.ABC là hình chóp đều nên góc
giữa hai mặt phẳng (ABC) và (A'BC) là  = 'A EH .
Tá có :
3 3 3
E , ,
2 3 6
a a a
A AH HE   
2 2
2 2 9 3a
A' '
3
b
H A A AH

   .
Do đó:
2 2
' 2 3
tan
A H b a
HE a


  ;
2 2 2 2
. ' ' '
3 3
' .
4 4
ABC ABC A B C ABC
a a b a
S V A H S 

   

34
2 2 2
'.
1 3
' .
3 12
A ABC ABC
a b a
V A H S

  .
Do đó: ' ' ' . ' ' ' '.A BB CC ABC A B C A ABCV V V 
.
2 2 2
' ' '
1 3
' .
3 6
A BB CC ABC
a b a
V A H S

  (đvtt)
ĐÁP ÁN ĐỀ THI THỬ SỐ 6
I 2 1,00
Xét phương trình 4 2
8 os 9 os 0c x c x m   với [0; ]x  (1)
Đặt osxt c , phương trình (1) trở thành: 4 2
8 9 0 (2)t t m  
Vì [0; ]x  nên [ 1;1]t   , giữa x và t có sự tương ứng một đối một, do đó số
nghiệm của phương trình (1) và (2) bằng nhau.
0,25
Ta có: 4 2
(2) 8 9 1 1 (3)t t m    
Gọi (C1): 4 2
8 9 1y t t   với [ 1;1]t   và (D): y = 1 – m.
Phương trình (3) là phương trình hoành độ giao điểm của (C1) và (D).
Chú ý rằng (C1) giống như đồ thị (C) trong miền 1 1t   .
0,25
Dựa vào đồ thị ta có kết luận sau:

81
32
m  : Phương trình đã cho vô nghiệm.
1.
81
32
m  : Phương trình đã cho có 2 nghiệm.

81
1
32
m  : Phương trình đã cho có 4 nghiệm.
 0 1m  : Phương trình đã cho có 2 nghiệm.
 0m  : Phương trình đã cho có 1 nghiệm.
 m < 0 : Phương trình đã cho vô nghiệm.
0,50
II 2,00
1 1,00
Phương trình đã cho tương đương:
33
loglog
3
2 0 22 0
111 log ln 0ln 01
222
222 0
xx
x xx
x xxx
xxx
     
  
                                  
0,50
3
2 2 2
log 0 1 1
21 1 3
ln 0 1
2 2 2
2 22
x x x
x x x
x
x x x
x xx
   
                                       
       
0,50
2 1,00

35
Điều kiện: | | | |x y
Đặt
2 2
; 0u x y u
v x y
   

 
; x y  không thỏa hệ nên xét x y  ta có
2
1
2
u
y v
v
 
  
 
.
Hệ phương trình đã cho có dạng:
2
12
12
2
u v
u u
v
v
 

 
  
 
0,25
4
8
u
v

 

hoặc
3
9
u
v



+
2 2
4 4
8 8
u x y
v x y
  
 
   
(I)
+
2 2
3 3
9 9
u x y
v x y
  
 
   
(II)
0,25
Giải hệ (I), (II). 0,25
Sau đó hợp các kết quả lại, ta được tập nghiệm của hệ phương trình
ban đầu là     5;3 , 5;4S 
0,25
Sau đó hợp các kết quả lại, ta được tập nghiệm của hệ phương trình
ban đầu là     5;3 , 5;4S 
1,00
III 0,25
Diện tích miền phẳng giới hạn bởi: 2
| 4 | ( )y x x C  và  : 2d y x
Phương trình hoành độ giao điểm của (C) và (d):
2 2 2
2 2
0 0 0
| 4 | 2 24 2 6 0
64 2 2 0
x x x
x x x xx x x x x
xx x x x x
   
                        
Suy ra diện tích cần tính:
   
2 6
2 2
0 2
4 2 4 2S x x x dx x x x dx      
0,25
Tính:  
2
2
0
| 4 | 2I x x x dx  
Vì   2
0;2 , 4 0x x x    nên 2 2
| 4 | 4x x x x    
 
2
2
0
4
4 2
3
I x x x dx    
0,25
Tính  
6
2
2
| 4 | 2K x x x dx  
Vì   2
2;4 , 4 0x x x    và   2
4;6 , 4 0x x x    nên
   
4 6
2 2
2 4
4 2 4 2 16K x x x dx x x x dx         .
0,25

36
Vậy
4 52
16
3 3
S   
1,00
IV 0,25
Gọi
H,
H’
là
tâm
của các tam giác đều ABC, A’B’C’.
Gọi I, I’ là trung điểm của AB, A’B’. Ta
có:      ' ' ' ' '
'
AB IC
AB CHH ABB A CII C
AB HH

   

Suy ra hình cầu nội tiếp hình chóp cụt này tiếp xúc với hai đáy tại H,
H’ và tiếp xúc với mặt bên (ABB’A’) tại điểm 'K II .
0,25
Gọi x là cạnh đáy nhỏ, theo giả thiết 2x là cạnh đáy lớn. Ta có:
1 3 1 3
' ' ' ' ' ;
3 6 3 3
x x
I K I H I C IK IH IC     
Tam giác IOI’ vuông ở O nên: 2 2 2 23 3
' . . 6r
6 3
x x
I K IK OK r x    
0,25
Thể tích hình chóp cụt tính bởi:  ' . '
3
h
V B B B B  
Trong đó:
2 2 2
2 24x 3 3 3r 3
3 6r 3; ' ; 2r
4 4 2
x
B x B h     
0,25
Từ đó, ta có:
2 2 3
2 22r 3r 3 3r 3 21r . 3
6r 3 6r 3.
3 2 2 3
V
 
    
 
 
0,25
V 1,00
Ta có:
+/  4sin3xsinx = 2 cos2x - cos4x ;
+/  4 os 3x - os x + 2 os 2x - os4x 2 sin 2x + cos4x
4 4 2
c c c c
        
        
      
+/  2 1 1
os 2x + 1 os 4x + 1 sin 4x
4 2 2 2
c c
     
       
    
Do đó phương trình đã cho tương đương:
 
1 1
2 os2x + sin2x sin 4x + m - 0 (1)
2 2
c  
Đặt os2x + sin2x = 2 os 2x -
4
t c c
 
  
 
(điều kiện: 2 2t   ).
0,25
Khi đó 2
sin 4x = 2sin2xcos2x = t 1 . Phương trình (1) trở thành:
2
4 2 2 0t t m    (2) với 2 2t  
2
(2) 4 2 2t t m   
Đây là phuơng trình hoành độ giao điểm của 2 đường ( ) : 2 2D y m  (là
đường song song với Ox và cắt trục tung tại điểm có tung độ 2 – 2m) và (P):
2
4y t t  với 2 2t   .
0,25

37
Trong đoạn 2; 2  
, hàm số 2
4y t t  đạt giá trị nhỏ nhất là 2 4 2
tại 2t   và đạt giá trị lớn nhất là 2 4 2 tại 2t  .
0,25
Do đó yêu cầu của bài toán thỏa mãn khi và chỉ khi
2 4 2 2 2 2 4 2m    
2 2 2 2m    .
0,25
VIa 2,00
1 1,00
Điểm  : 1 0 ;1C CD x y C t t      .
Suy ra trung điểm M của AC là
1 3
;
2 2
t t
M
  
 
 
. 0,25
Điểm  
1 3
: 2 1 0 2 1 0 7 7;8
2 2
t t
M BM x y t C
  
             
 
0
,
2
5
0
,
2
5
Từ A(1;2), kẻ : 1 0AK CD x y    tại I (điểm K BC ).
Suy ra    : 1 2 0 1 0AK x y x y        .
Tọa độ điểm I thỏa hệ:  
1 0
0;1
1 0
x y
I
x y
  

  
.
Tam giác ACK cân tại C nên I là trung điểm của AK  tọa độ của  1;0K  .
Đường thẳng BC đi qua C, K nên có phương trình:
1
4 3 4 0
7 1 8
x y
x y

    
 
2
Gọi (P) là mặt phẳng đi qua đường thẳng
 , thì ( ) //( )P D hoặc ( ) ( )P D . Gọi H là
hình chiếu vuông góc của I trên (P). Ta
luôn có IH IA và IH AH .
Mặt khác
       
 
, ,d D P d I P IH
H P
  


Trong mặt phẳng  P , IH IA ; do đó axIH = IA H Am   . Lúc này (P) ở vị trí
(P0) vuông góc với IA tại A.
Vectơ pháp tuyến của (P0) là  6;0; 3n IA  
 
, cùng phương với  2;0; 1v  

.
Phương trình của mặt phẳng (P0) là:    2 4 1. 1 2x - z - 9 = 0x z    .
VIIa
Để ý rằng       1 1 1 0xy x y x y       ;
và tương tự ta cũng có
1
1
yz y z
zx z x
  

  
0,25

38
Vì vậy ta có:
 
1 1 1
1 1 1
1 1 1 1 1 1
3
1 zx+y
1
5
1
1 5
5
x y z
x y z
xy yz zx yz zx xy
x y z
yz xy z
z y
x
yz zx y xy z
z y
x
z y y z
 
          
      
   
 
 
    
   
 
    
  

vv
1,00
Ta có:
 1;2 5AB AB   

.
Phương trình của AB là:
2 2 0x y   .
   : ;I d y x I t t   . I là
trung điểm của AC và BD
nên ta có:
   2 1;2 , 2 ;2 2C t t D t t  .
0,25
Mặt khác: D . 4ABCS AB CH  (CH: chiều cao)
4
5
CH  . 0,25
Ngoài ra:  
   
4 5 8 8 2
; , ;| 6 4 | 4
3 3 3 3 3;
5 5
0 1;0 , 0; 2
t C Dt
d C AB CH
t C D
    
     
       
    
Vậy tọa độ của C và D là
5 8 8 2
; , ;
3 3 3 3
C D
   
   
   
hoặc    1;0 , 0; 2C D 
0,50
2 1,00
Gọi P là chu vi của tam giác MAB thì P = AB + AM + BM.
Vì AB không đổi nên P nhỏ nhất khi và chỉ khi AM + BM nhỏ nhất.
Đường thẳng  có phương trình tham số:
1 2
1
2
x t
y t
z t
  

 
 
.
Điểm M  nên  1 2 ;1 ;2M t t t   .
         
         
       
22 2 2 22
22 2 2 22
2 22 2
2 2 4 2 9 20 3 2 5
4 2 2 6 2 9 36 56 3 6 2 5
3 2 5 3 6 2 5
AM t t t t t
BM t t t t t t
AM BM t t
          
              
     
0,25
Trong mặt phẳng tọa độ Oxy, ta xét hai vectơ  3 ;2 5u t

và
 3 6;2 5v t  

.
Ta có
   
   
22
22
| | 3 2 5
| | 3 6 2 5
u t
v t

 

   



0,25

39
Suy ra | | | |AM BM u v  
 
và  6;4 5 | | 2 29u v u v    
   
Mặt khác, với hai vectơ ,u v
 
ta luôn có | | | | | |u v u v  
   
Như vậy 2 29AM BM 
Đẳng thức xảy ra khi và chỉ khi ,u v
 
cùng hướng
3 2 5
1
3 6 2 5
t
t
t
   
 
 1;0;2M và  min 2 29AM BM  .
0,25
Vậy khi M(1;0;2) thì minP =  2 11 29 0,25
VIIb 1,00
Vì a, b, c là ba cạnh tam giác nên:
a b c
b c a
c a b
 

 
  
.
Đặt  , , , , 0 , ,
2 2
a b c a
x y a z x y z x y z y z x z x y
 
           .
Vế trái viết lại:
2
3 3 2
a b a c a
VT
a c a b a b c
x y z
y z z x x y
 
  
   
  
  
0,50
Ta có:    
2
2
z z
x y z z x y z z x y
x y z x y
        
  
.
Tương tự:
2 2
; .
x x y y
y z x y z z x x y z
 
     
Do đó:
 2
2
x y zx y z
y z z x x y x y z
 
   
    
.
Tức là:
1 1 2
2
3 3 2 3 3
b c
a
a b a c a b c a c a b
 
     
      
0,50
HƯỚNG DẨN GIẢI (ĐỀ SỐ 7)
I:PHẦN CHUNG CHO TẤT CẢ CÁC THÍ SINH (7,0 điểm)
CâuI.1.(Học sinh tự giải)
2)Phương trình hoành độ điểm chung của (Cm) và d là:

            
    
3 2 2
2
0
2 ( 3) 4 4 (1) ( 2 2) 0
( ) 2 2 0 (2)
x
x mx m x x x x mx m
g x x mx m
(d) cắt (Cm) tại ba điểm phân biệt A(0; 4), B, C phương trình (2) có 2 nghiệm phân biệt khác 0.
        
  
    
/ 2
1 22 0
( )
2(0) 2 0
m mm m
a
mg m
.
Mặt khác:
 
 
1 3 4
( , ) 2
2
d K d Do đó: 
      218 2 . ( , ) 8 2 16 256
2KBC
S BC d K d BC BC
2 2
( ) ( ) 256B C B Cx x y y     với ,B Cx x là hai nghiệm của phương trình (2).
             2 2 2 2
( ) (( 4) ( 4)) 256 2( ) 256 ( ) 4 128B C B C B C B C B Cx x x x x x x x x x
2 2 1 1374 4( 2) 128 34 0
2
m m m m m           (thỏa ĐK (a)). Vậy 1 137
2
m 

40
CâuII:1. Phương trình  (cosx–sinx)2
- 4(cosx–sinx) – 5 = 0
cos -sin -1
cos -sin 5( cos -sin 2)
x x
x x loai vi x x

 
 
2
22sin( ) 1 sin( ) sin ( )
4 4 4 2
x k
x x k Z
x k
   
 
  
       
  
2) HÖ ph¬ng tr×nh t¬ng ®¬ng víi
2
2
1
( 2) 2
1
( 2) 1
x
x y
y
x
x y
y
 
   


   

§Æt 2yxv,
y
1x
u
2



Ta cã hÖ 1vu
1uv
2vu






Suy ra








12yx
1
y
1x2
.
Gi¶i hÖ trªn ta ®îc nghiÖm cña hpt ®· cho lµ (1; 2), (2; 5)
CâuIII:1. Ta có: I =
2 2
6
1
sin sin
2


  x x dx =
2
2
6
3
sin cos
2
x x dx


   . Đặt
3
cos cos
2
x t 
Đổi cận: Khi
2
x cos
6 2 4
t t
 
     ; khi x cos 0
2 2
t t
 
     .
Do vậy:
2
2
4
3
sin
2
I tdt


   =  
3
2
16
  .
2. Tìm các giá trị của tham số thực m sao cho phương trình sau có nghiệm thực:
2 2
1 1 1 1
9 ( 2)3 2 1 0x x
m m   
     (1)
* Đk [-1;1]x  , đặt t =
2
1 1
3 x 
; [-1;1]x   [3;9]t 
Ta có: (1) viết lại
2
2 2 2 1
( 2) 2 1 0 ( 2) 2 1
2
t t
t m t m t m t t m
t
 
           

Xét hàm số f(t) =
2
2 1
2
t t
t
 

, với [3;9]t  . Ta có:
2
/ /
14 3
( ) , ( ) 0
3( 2)
tt t
f t f t
tt
 
     
Lập bảng biến thiên
t 3 9
f/
(t) +
f(t)
48
7
4
Căn cứ bảng biến thiêng, (1) có nghiệm [-1;1]x   (2) có nghiệm [3;9]t   484
7
m 
CâuIV:Gọi M là trung điểm của BC và O là hình chiếu của S lên AM.
Suy ra: SM =AM = 3
2
a ;  0
60AMS  và SO  mp(ABC)
 d(S; BAC) = SO = 3
4
a
Gọi VSABC là thể tích của khối chóp S.ABC
 VS.ABC =
3
31 .
3 16ABC
aS SO  (đvtt)
Mặt khác, VS.ABC = 1 . ( ; )
3 SACS d B SAC
C
S
O M
A

41
SAC cân tại C có CS =CA =a; SA = 3
2
a

2
13 3
16SAC
aS 
Vậy: d(B; SAC) = .3 3
13
S ABC
SAC
V a
S
 (đvđd).
II. PHẦN RIÊNG (3.0 điểm)
C©u V.a 1ViÕt ph¬ng tr×nh ®êng trßn ®i qua giao ®iÓm cña(E) vµ (P)
Hoµnh ®é giao ®iÓm cña (E) vµ (P) lµ nghiÖm cña ph¬ng tr×nh
09x37x36x91)x2x(
9
x 23422
2
 (*)
XÐt 9x37x36x9)x(f 234
 , f(x) liªn tôc trªn R cã f(-1)f(0) < 0,
f(0)f(1) < 0, f(1)f(2) < 0, f(2)f(3) < 0 suy ra (*) cã 4 nghiÖm ph©n biÖt, do ®ã (E) c¾t (P) t¹i 4 ®iÓm
ph©n biÖt
To¹ ®é c¸c giao ®iÓm cña (E) vµ (P) tháa m·n hÖ







1y
9
x
x2xy
2
2
2
09y8x16y9x9
9y9x
y8x16x8 22
22
2






 (**)
(**) lµ ph¬ng tr×nh cña ®êng trßn cã t©m 






9
4
;
9
8
I , b¸n kÝnh R =
9
161
Do ®ã 4 giao ®iÓm cña (E) vµ (P) cïng n»m trªn ®êng trßn cã ph¬ng tr×nh (**)
2.ViÕt ph¬ng tr×nh mÆt ph¼ng ()....
Do () // () nªn () cã ph¬ng tr×nh 2x + 2y z + D = 0 (D 17)
MÆt cÇu (S) cã t©m I(1; -2; 3), b¸n kÝnh R = 5
§êng trßn cã chu vi 6 nªn cã b¸n kÝnh r = 3.
Kho¶ng c¸ch tõ I tíi () lµ h = 435rR 2222

Do ®ã 







(lo¹i)17D
7D
12D54
)1(22
D3)2(21.2
222
VËy () cã ph¬ng tr×nh 2x + 2y z - 7 = 0
C©u VI.a T×m hÖ sè cña sè h¹ng chøa x2
trong khai triÓn nhÞ thøc Niut¬n cña
n
x
x 





 4
2
1
,
biÕt r»ng n lµ sè nguyªn d¬ng tháa m·n:
1
6560
1
2
3
2
2
2
2
1
2
3
1
2
0





n
C
n
CCC n
n
n
nnn 
BG: Ta có
  
2
0
nn
n
22
n
1
n
0
n
2
0
n
dxxCxCxCCdx)x1(I 
2
0
1nn
n
32
n
21
n
0
n xC
1n
1
xC
3
1
xC
2
1
xC 






 

suy ra I n
n
1n
2
n
3
1
n
2
0
n C
1n
2
C
3
2
C
2
2
C2



 (1)
MÆt kh¸c
1n
13
)x1(
1n
1
I
1n
2
0
1n







(2)
Tõ (1) vµ (2) ta cã n
n
1n
2
n
3
1
n
2
0
n C
1n
2
C
3
2
C
2
2
C2




1n
13 1n




Theo bµi ra th× 7n65613
1n
6560
1n
13 1n
1n




 

Ta cã khai triÓn   















7
0
4
k314
k
7k
k7
0
4
k7
k
7
7
4
xC
2
1
x2
1
xC
x2
1
x

42
Sè h¹ng chøa x2
øng víi k tháa m·n 2k2
4
k314


VËy hÖ sè cÇn t×m lµ
4
21
C
2
1 2
72

CâuVb *1.Gọi H là hình chiếu của A trên d, mặt phẳng (P) đi qua A và (P)//d, khi đó
khoảng cách giữa d và (P) là khoảng cách từ H đến (P).
Giả sử điểm I là hình chiếu của H lên (P), ta có HIAH  => HI lớn nhất khi IA 
Vậy (P) cần tìm là mặt phẳng đi qua A và nhận AH làm véctơ pháp tuyến.
Mặt khác, )31;;21( tttHdH  vì H là hình chiếu của A trên d nên
. 0 ( (2;1;3)AH d AH u u   
  
là véc tơ chỉ phương của d) )5;1;7()4;1;3(  AHH
Vậy: (P): 7(x – 10) + (y – 2) – 5(z + 1) = 0 7x + y – 5z –77 = 0
2.*Gọi C(a; b) , (AB): x –y –5 =0  d(C; AB) =
5 2
2
ABCa b S
AB
 


8(1)
5 3
2(2)
a b
a b
a b
 
      
; Trọng tâm G  5 5;
3 3
a b   (d)  3a –b =4 (3)
Từ (1), (3)  C(–2; 10)  r = 3
2 65 89
S
p

 
Từ (2), (3)  C(1; –1)  3
2 2 5
Sr
p
 

.
CâuVIb: Vì z = 1 + i là một nghiệm của phương trình: z2
+ bx + c = 0 ( b, c  R), nên ta có :
     
2 0 2
1 1 0 2 0
2 0 2
b c b
i b i c b c b i
b c
    
            
   
KẾT QUẢ ĐỀ 8
Câu I (2,0 điểm) 1. Tự giải 2. m 2
Câu II (2,0 điểm) 1.
k2
x k2 ;x
6 3
 
    2. x 2;x 1 33  
Câu III (1,0 điểm)
4
I ln
3

Câu IV (1,0 điểm) V 8 3
Câu V (1,0 điểm) minS 5
Câu VIa (2.0 điểm) 1. x 3y 6 0;x y 2 0      2. 1 2C (0;0; 3),C (0;0; 3)
Câu VII.a (1,0 điểm) 192 số
Câu VIb (2,0 điểm) 1. x 2y 6 0   2. 1 2D (0; 7;0),D (0;8;0)
Câu VII.b (1,0 điểm) 64 số
Hết
ĐÁP ÁN ĐỀ SỐ 9
Câu NỘI DUNG Điểm
Câu I.
b) 9)1(63' 2
 xmxy
Để hàm số có cực đại, cực tiểu:
09.3)1(9' 2
 m
03)1( 2
 m
);31()31;(  m
0,25đ
-2 1

43
Ta có   14)22(29)1(63
3
1
3
1 22





 
 mxmmxmx
m
xy
Gọi tọa độ điểm cực đại và cực tiểu là (x1; y1) và (x2; y2)
14)22(2 1
2
1  mxmmy
14)22(2 2
2
2  mxmmy
Vậy đường thẳng đi qua hai điểm cực đại và cực tiểu là
14)22(2 2
 mxmmy
Vì hai điểm cực đại và cực tiểu đối xứng qua đt xy
2
1
 ta có điều kiện cần
là
  1
2
1
.)22(2 2
 mm
1222
 mm






3
1
0322
m
m
mm
Theo định lí Viet ta có:





3.
)1(2
21
21
xx
mxx
Khi m = 1 ptđt đi qua hai điểm CĐ và CT là:
y = 2x + 5. Tọa độ trung điểm CĐ và CT là:












1
2
10)(2
2
2
2
4
2
2121
21
xxyy
xx
Tọa độ trung điểm CĐ và CT là (2; 1) thuộc đường thẳng xy
2
1
 1 m
thỏa mãn.
Khi m = 3 ptđt đi qua hai điểm CĐ và CT là: y = 2x – 11. Tọa độ trung
điểm CĐ và CT là:












9
2
10)(2
2
2
2
2121
21
xxyy
xx
Tọa độ trung điểm CĐ và CT là (2; 9) không thuộc đường thẳng
xy
2
1
 3 m không thỏa mãn.
Vậy m = 1 thỏa mãn điều kiện đề bài.
1) Giải phương trình:
)sincos.3(833cos36cos.32cos.sin6cos.sin2
033)sincos.3(82cos.33cos.32)3(cos2sin
232
3


xxxxxxxx
xxxxxx
0)sincos3(8)sincos3(cos.6)sincos3(cos2 2
 xxxxxxxx

















)(4cos
1cos
3tan
04cos3cos
0sincos3
0)8cos6cos2)(sincos3(
2
2
loaix
x
x
xx
xx
xxxx







 k
kx
kx
,
2
3



0,25đ
0,5đ
0,25đ
0,25đ
0,25đ

44
Câu II.
2) Giải bất phương trình:
)
7
1
(log)54(log
2
1
2
1
2
2


x
xx (1)
Đk:











7
);1()5;(
07
0542
x
x
x
xx
)1()5;7(  x
Từ (1)
7
1
log2)54(log 2
2
2


x
xx
5
27
5410
491454
)7(log)54(log
22
2
2
2
2





x
x
xxxx
xxx
Kết hợp điều kiện: Vậy BPT có nghiệm: )
5
27
;7(

x
3) Ta có: x.sin2x = 2x
 x.sin2x – 2x = 0  x(sin2x – 2) =0
 x = 0
Diện tích hình phẳng là:
  2
0
2
0
)22(sin)22sin.(

dxxxdxxxxS
Đặt














x
x
v
dxdu
dxxdv
xu
2
2
2cos
)22(sin
 





 2
0
2
0
2
2
2
2cos
2
2
2cos.
(


dxx
x
x
xx
S
2
0
2
2
4
2sin
24








 x
x
S
44424
222

 S (đvdt)
Gọi Q, I, J lần lượt là
trung điểm B’C’, BB’, CC’
ta có:
2
3a
AP 
3aAH 
Vì '' AHA vuông cân tại H.
Vậy 3' aHA 
HASV ABCCBABCA '.''' 
Ta có
4
3
2
3
.
2
1 2
aa
aSABC  (đvdt)
0,25đ
0,5đ
0,25đ
0,25đ
0,25đ
0,25đ
0,25đ
0,25đ
0,25đ
45
E
K
J
I
A
B
C
C'
B'
A'
P
H
Q
N
M

45
Câu III.
4
3
4
3
.3
32
'''
aa
aV CBABCA  (đvtt) (1)
Vì '' AHA vuông cân  CCBBHKAAHK ''' 
G ọi E = MN KH BM = PE = CN (2)
mà AA’ = 22
' AHHA  = 633 22
aaa 
4
6
2
6 a
CNPEBM
a
AK 
Ta có thể tích K.MNJI là:
1
.
3
1 1 6
'
2 4 4
MNJIV S KE
a
KE KH AA

  
2
6 6
. . ( )
4 4
MNJI
a a
S MN MI a dvdt  
2 3
1 6 6
( )
3 4 4 8
KMNJI
a a a
V dvtt  
3 3
2 3
' ' '
3
18 8
3 2
8 8
ABCKMN
A B C KMN
a a
V
a aV

  

2) Giải hệ phương trình sau trong tập số phức:









06)()(
5
6
222
2
2
aabbaa
aa
aa
ĐK: 02
 aa
Từ (1) 06)(5)( 222
 aaaa







6
1
2
2
aa
aa
Khi 12
 aa thay vào (2)













2
.231
2
.231
06
06
2
2
i
b
i
b
bb
bb











2
31
2
31
012
i
a
i
a
aa
Khi 62
 aa






2
3
a
a
Thay vào (2)
0,25đ
0,25đ
0,25đ
0,25đ
0,2 5đ
0,25đ

46
Câu IV:













2
51
2
51
01
0666
2
2
b
b
bb
bb
Vậy hệ pt có nghiệm (a, b) là:







 







 
2
31
;
2
231
,
2
31
;
2
231 iiii







 







 
2
31
;
2
231
,
2
31
;
2
231 iiii







 







 







 







 

2
51
;2,
2
51
;2,
2
51
;3,
2
51
;3









720
2
19
2
9
1
12
3
2
n
mn
m
m
P
AcC
Từ (2): 761!6720)!1(  nnn (3)
Thay n = 7 vào (1)
)!1(
!
.
2
19
9
!8!2
!10
)!2(!2
!




m
m
m
m
09920
19990
2
19
2
9
45
2
)1(
2
2





mm
mmm
m
mm
119  m vì 10 mm
Vậy m = 10, n = 7. Vậy ta có 10 bông hồng trắng và 7 bông hồng nhung, để
lấy được ít nhất 3 bông hồng nhung trong 5 bông hồng ta có các TH sau:
TH1: 3 bông hồng nhung, 2 bông hồng trắng có:
1575. 2
10
3
7 CC cách
TH2: 4 bông hồng nhung, 1 bông hồng trắng có:
350. 1
10
4
7 CC cách
TH3: 5 bông hồng nhung có:
215
7 C cách
có 1575 + 350 + 21 = 1946 cách.
Số cách lấy 4 bông hồng thường
%45,31
6188
1946
61885
17


P
C
2) Gọi ptđt // Oy là: x = a (d) tung độ giao điểm (d) và Elip là:
25
25
25
1
9
1
925
222
22
aay
ya



0,25đ
0,25đ
0,25đ
0,25đ

47
Câu V:
2
2
2
25
5
3
25
25
.9 ay
a
y 


Vậy 











 22
25
5
3
;,25
5
3
; aaBaaA






 2
25
5
6
;0 aAB
9
125
9
100
25
9
100
25
3
10
25
425
5
6
||
222
2


aaa
aAB
3
55
 a
Vậy phương trình đường thẳng:
3
55
,
3
55


 xx
3)đường thẳng d2 có PTTS là:








'51
'2
'21
tz
ty
tx
vectơ CP của d1 và d2 là: 1 2
(1;1; 1), (2;1;5)d du u  

VTPT của mp( ) là 1 2
. (6; 7; 1)d dn u u
     
  
pt mp( ) có dạng 6x – 7y – z + D = 0
Đường thẳng d1 và d2 lần lượt đi qua 2đ’ M(2; 2; 3) và N(1; 2; 1)
( ,( )) ( ,( ))
|12 14 3 | | 6 14 1 |
| 5 | | 9 | 7
d M d N
D D
D D D
  
      
       
Vậy PT mp( ) là: 3x – y – 4z +7 0
Ta có: P + 3 = 2
2
3
2
2
3
2
2
3
111
a
a
c
c
c
b
b
b
a






24
1
121224
6 2
2
2
2
3
b
b
a
b
a
P






24
1
1212
2
2
2
2
3
c
c
b
c
b 





24
1
1212
2
2
2
2
3
a
a
c
a
c 





3
6
3
6
3
6
216
3
216
3
216
3
cba

6
222
3 82
9
)(
222
3
22
3
 cbaP
2
3
22
3
22
9
22
3
22
9
6 3
 P
Để PMin khi a = b = c = 1
0,25đ
0,25đ
0,25đ
0,25đ
0,25đ
0,25đ
0,25đ
0,25đ

48
HƯỚNG DẪN GIẢI ĐẾ 10
Câu I.
1. (Tự giải)
2. Pt : x3
+ mx + 2 = 0
x
xm
22
 ( x )0
Xét f(x) = 2
2 2
2)('
2
x
xxf
x
x  = 2
3
22
x
x 
Ta có x  0 1 +
f’(x) + + 0
f(x) + 3
  
Đồ thị hàm số (1) cắt trục hòanh tại một điểm duy nhất 3 m .
Câu II.
1.













)2(022
)1(1
22
1
2233
33
322
33
xyyxyx
yx
yxyyx
yx
y 0 . Ta có:
























)4(0122
)3(1
23
33
y
x
y
x
y
x
yx
Đặt : t
y
x
 (4) có dạng : 2t3
– t2
– 2t + 1 = 0  t = ,1 t =
2
1
.
a) Nếu t = 1 ta có hệ 3
33
2
11






yx
yx
yx
b) Nếu t = 1 ta có hệ 





yx
yx 133
hệ vô nghiệm.
c) Nếu t =
2
1
ta có hệ
3
32
,
3
3
2
1 3333






yx
xy
yx
2. Pt xxx tansin2)
4
(sin2 22


(cosx )0 xxxxx sincos.sin2cos)]
2
2cos(1[ 2


 (1 sin2x)(cosx – sinx) = 0  sìn2x = 1 hoặc tanx = 1.
Câu III.
I =  



2
1
2
1
2
22
44
xdx
x
x
dx
x
x
.
Đặt t = xdxtdtxtx  222
44
I =
0
3
2
0
3
0
3
0
3
2
2
2
2
2
ln)
4
4
1(
44
)(















   t
t
tdt
t
dt
t
t
t
tdtt
=











32
32
ln3
Câu IV.

49
h
H
M
D
CB
A
S
SH  BM và SA BM suy ra AH  BM
VSABH = BHAH
h
BHAHSA .
6
..
6
1
 .
VSABH lớn nhất khi AH.BH lớn nhất. Ta có: AH + BH BHAH.2 BHAHBHAH .222

BHAHa .22
 , vậy AH.BH lớn nhất khi AH.BH =
2
2
a
khi AH = BH khi H là tâm của hình
vuông , khi M D . Khi đó VSABH =
12
2
ha
.
Câu V. mxx 4 2
1
D = [0 ; + )
*Đặt f(x) =
x
x
x
x
xx
xx
xxx
xx
x
xfxx
.)
1
1(2
)
1
1(
.)1(2
)1(
2
1
)1(2
)('1
4
3
2
2
3
4
3
2
2
3
2
3
4 32
4 32
4 32
4 2








Suy ra: f’(x) = );0(0
.)
1
1(2
)
1
1(1
4
3
2
4
3
2



x
x
x
x
* 0
)1)(1(
1
lim
1
1
lim)1(lim
24 2
22
4 2
2
4 2
























xxxx
xx
xx
xx
xx
xxx
* BBT x 0 +
f’(x)
f(x) 1
0
Vậy: 0 < m 1
Câu VI a.
1.d1:





ty
tx 23
, I );3(1 ttId 
d(I , d2) = 2
11
7
,
11
27
101711  ttt

50
 t = 4
11
27
11
21
:)(
11
27
;
11
21
11
27
22
11 

















 yxCI
 t = 4
11
7
11
19
:)(
11
7
;
11
19
11
7
22
22 
















 
 yxCI
2. )1;;21(),2;;(,
1
21
:,
2
: 22221111
2
2
2
2
1
1
1
1 tttNdNtttMdM
tz
ty
tx
d
tz
ty
tx
d 
















)21;;21( 121212 ttttttMN 
Theo gt :

























13
12
;0
21
01213
21
6
0.
6
)//(
22
21
2
2
2
21
2 tt
tt
tt
tt
MN
nMN
MN
PMN
* )1;0;1(,)2;1;1(,10 12  NMtt
* 














13
11
;
13
12
;
13
11
,
13
22
;
13
11
;
13
11
,
13
11
13
12
12 NMtt
Câu VII a.
0111
224









































iz
iz
iz
iz
iz
iz
* 01
2








iz
iz
01 


 z
iz
iz
* 0001 2
22












































i
iz
iz
i
iz
iz
i
iz
iz
iz
iz
1 z
Câu VI b.
1.B(11; 5)
AC: kx – y – 2k + 1 = 0
cos CAB = cos DBA
7
1
;10187
1
2
2
3 2
2



 kkkk
k
k
 k = 1 , AC : x – y – 1 = 0
 k =
7
1
, AC : x – 7y + 5 = 0 // BD ( lọai)
Ta tìm được A(1 ; 0), C(6 ; 5), D(4 ; 0)
2.(S): x2
+ y2
+ z2
+ 2ax + 2by + 2cz + d = 0 có tâm I(a ; b ; c) , R = dcba  222
.
O, A, B thuộc (S) ta có : d = 0 , a = 1, c = 2
d(I, (P)) = 5,0552
3
5
 bbb
 b = 0 , (S): x2
+ y2
+ z2
2x – 4z = 0
 b = 5 , (S) : x2
+ y2
+ z2
– 2x + 10y – 4z = 0
Câu VII b.
ĐK :








3
1
0
x
x
x
Bất phương trình trở thành : 0
1log
1
log
1
1log
1
log
1
3
log
1
log
1
3333
3
3





xxxxxx
1log0log0)1(loglog0
)1(loglog
1
3333
33



 xxxx
xx

51
* 10log3  xx kết hợp ĐK : 0 < x < 1
* 30log3  xx
Vậy tập nghiệm của BPT: x );3()1;0( 
HƯỚNG DẨN GIẢI (đề 11)
Câu I. 2/Tacã 





mx
0x
0)mx(x3mx3x3'y 2
ta thÊy víi 0m  th× y’ ®æi dÊu khi ®i qua c¸c nghiÖm do vËy hµm sè cã C§,CT
+NÕu m>0 hµm sè cã C§ t¹i x=0 vµ
3
MAX m
2
1
y  ;cã CT t¹i x=m vµ 0yMIN 
+NÕu m<0 hµm sè cã C§ t¹i x=m vµ 0yMAX  ;cã CT t¹i x=0 vµ
3
MIN m
2
1
y 
Gäi A vµ B lµ c¸c ®iÓm cùc trÞ cña hµm sè.§Ó A vµ B ®èi xøng víi nhau qua ®êng ph©n gi¸c
y=x,®iÒu kiÖn ¾t cã vµ ®ñ lµ OBOA  tøc lµ: 2m2mm
2
1
m 23

Câu V.a ( 2,0 điểm ) : Phương trình mặt phẳng (P) qua O nên có dạng : Ax + By + Cz = 0
với 2 2 2A B C 0  
Vì (P)  (Q) nên 1.A+1.B+1.C = 0  A+B+C = 0 C A B    (1)
Theo đề :
d(M;(P)) = 2
A 2B C 2 2 2 22 (A 2B C) 2(A B C )
2 2 2A B C
 
       
 
(2)
Thay (1) vào (2) , ta được : 8AB+5
8A2B 0 B 0 hay B =
5
   

(1)
B 0 C A . Cho A 1,C 1       thì (P) : x z 0 

8A
B =
5
 . Chọn A = 5 , B = 1
(1)
C 3  thì (P) : 5x 8y 3z 0  
CâuVb1 Chọn A(2;3;3),B(6;5; 2)(d) mà A,B nằm trên (P) nên (d) nằm trên (P) .
Gọi u

vectơ chỉ phương của (d1) qua A và vuông góc với (d) thì
u ud
u uP
 


 
 
nên ta chọn u [u,u ] (3; 9;6) 3(1; 3;2)P    
  
. Ptrình của đường thẳng (d1)
:
 

  
   
x 2 3t
y 3 9t (t R)
z 3 6t
(  ) là đường thẳng qua M và song song với (d ). Lấy M trên (d1) thì M(2+3t;3 9t;3+6t) .
Theo đề :
1 12 2 2 2AM 14 9t 81t 36t 14 t t
9 3
         

52
+ t =
1
3
 M(1;6;5)
x 1 y 6 z 5
( ):1 4 2 1
  
   
+ t =
1
3
M(3;0; 1)
x 3 y z 1
( ):2 4 2 1
 
   
Đ¸p ¸n ®Ò số 12 thi thö ®¹i häc lÇn 1 khèi a
I.PhÇn dµnh cho tÊt c¶ c¸c thÝ sÝnh
I 2. (0,75 ®iÓm)
Hoµnh ®é giao ®iÓm cña ®å thÞ (C ) vµ ®êng th¼ng d lµ nghiÖm cña ph¬ng
tr×nh








)1(021)4(
2
2
12
2
mxmx
x
mx
x
x
Do (1) cã mmmvam  0321)2).(4()2(01 22
nªn ®êng
th¼ng d lu«n lu«n c¾t ®å thÞ (C ) t¹i hai ®iÓm ph©n biÖt A, B
0,25
Ta cã yA = m xA; yB = m xB nªn AB2
= (xA xB)2
+ (yA yB)2
= 2(m2
+ 12)
suy ra AB ng¾n nhÊt  AB2
nhá nhÊt  m = 0. Khi ®ã 24AB
0,5
II
(2
®iÓm)
1. (1 ®iÓm)
Ph¬ng tr×nh ®· cho t¬ng ®¬ng víi
9sinx + 6cosx 6sinx.cosx + 1 2sin2
x = 8
 6cosx(1 sinx) (2sin2
x 9sinx + 7) = 0
 6cosx(1 sinx) (sinx 1)(2sinx 7) = 0
0,5
 (1-sinx)(6cosx + 2sinx 7) = 0
 




)(07sin2cos6
0sin1
VNxx
x
0,25
 

2
2
kx 
0,25
2. (1 ®iÓm)
§K:





03loglog
0
2
2
2
2 xx
x
BÊt ph¬ng tr×nh ®· cho t¬ng ®¬ng víi
)1()3(log53loglog 2
2
2
2
2  xxx
®Æt t = log2x,
BPT (1)  )3(5)1)(3()3(5322
 tttttt
0,5























4log3
1log
43
1
)3(5)3)(1(
3
1
2
2
2
x
x
t
t
ttt
t
t 0,25







168
2
1
0
x
x
VËy BPT ®· cho cã tËp nghiÖm lµ: )16;8(]
2
1
;0( 
III
1 ®iÓm  
xx
dx
xxx
dx
I 23233
cos.2sin
8
cos.cos.sin
®Æt tanx = t 0,5

53
dt
t
t
t
t
dt
I
t
t
x
x
dx
dt
 






3
32
3
2
22
)1(
)
1
2
(
8
1
2
2sin;
cos
C
x
xxxdtt
t
tt
dt
t
ttt






2
2433
3
246
tan2
1
tanln3tan
2
3
tan
4
1
)
3
3(
133
0,5
C©u IV
1 ®iÓm Do )( 111 CBAAH  nªn gãc HAA1 lµ gãc gi÷a AA1 vµ (A1B1C1), theo gi¶ thiÕt
th× gãc HAA1 b»ng 300
. XÐt tam gi¸c vu«ng AHA1 cã AA1 = a, gãc
HAA1 =300
2
3
1
a
HA  . Do tam gi¸c A1B1C1 lµ tam gi¸c ®Òu c¹nh a, H
thuéc B1C1 vµ
2
3
1
a
HA  nªn A1H vu«ng gãc víi B1C1. MÆt kh¸c 11CBAH 
nªn )( 111 HAACB 
0,5
KÎ ®êng cao HK cña tam gi¸c AA1H th× HK chÝnh lµ kho¶ng c¸ch gi÷a AA1
vµ B1C1
0,25
Ta cã AA1.HK = A1H.AH
4
3.
1
1 a
AA
AHHA
HK 
0,25
C©u V
1 ®iÓm
¸p dông bÊt ®¼ng thøc C« si cho 2005 sè 1 vµ 4 sè a2009
ta cã
1(.2009....20091...11 42009 20092009200920092009200920092009
2005
aaaaaaaaa  
T¬ng tù ta cã
)2(.2009....20091...11 42009 20092009200920092009200920092009
2005
bbbbbbbbb  
)3(.2009....20091...11 42009 20092009200920092009200920092009
2005
ccccccccc  
0,5
A1
A B
C
C
B1
K
H

54
Céng theo vÕ (1), (2), (3) ta ®îc
)(20096027
)(2009)(46015
444
444200920092009
cba
cbacba


Tõ ®ã suy ra 3444
 cbaP
MÆt kh¸c t¹i a = b = c = 1 th× P = 3 nªn gi¸ trÞ lín nhÊt cña P = 3.
0,5
PhÇn riªng.
1.Ban c¬ b¶n
C©u
VIa
2
®iÓm
1.( 1 ®iÓm)
Tõ ph¬ng tr×nh chÝnh t¾c cña ®êng trßn ta cã t©m I(1;-2), R = 3, tõ A kÎ ®îc
2 tiÕp tuyÕn AB, AC tíi ®êng trßn vµ ACAB  => tø gi¸c ABIC lµ h×nh vu«ng
c¹nh b»ng 3 23 IA
0,5








7
5
6123
2
1
m
m
m
m
0,5
2. (1 ®iÓm)
Gäi H lµ h×nh chiÕu cña A trªn d, mÆt ph¼ng (P) ®i qua A vµ (P)//d, khi ®ã
kho¶ng çch gi÷a d vµ (P) lµ kho¶ng çch tõ H ®Õn (P).
Gi¶ sö ®iÓm I lµ h×nh chiÕu cña H lªn (P), ta cã HIAH  => HI lín nhÊt khi
IA 
VËy (P) cÇn t×m lµ mÆt ph¼ng ®i qua A vµ nhËn AH lµm vÐc t¬ ph¸p tuyÕn.
0,5
)31;;21( tttHdH  v× H lµ h×nh chiÕu cña A trªn d nªn
)3;1;2((0.  uuAHdAH lµ vÐc t¬ chØ ph¬ng cña d)
)5;1;7()4;1;3(  AHH VËy (P): 7(x 10) + (y 2) 5(z + 1) = 0
 7x + y -5z -77 = 0
0,5
C©u
VIIa
1
®iÓm
Tõ gi¶ thiÕt bµi to¸n ta thÊy cã 62
4 C çch chän 2 ch÷ sè ch½n (v× kh«ng cã sè
0)vµ 102
5 C çch chän 2 ch÷ sè lÏ => cã 2
5C . 2
5C = 60 bé 4 sè tháa m·n bµi to¸n
0,5
Mçi bé 4 sè nh thÕ cã 4! sè ®îc thµnh lËp. VËy cã tÊt c¶ 2
4C . 2
5C .4! = 1440 sè 0,5
2.Ban n©ng cao.
C©u
VIa
2
®iÓm
1.( 1 ®iÓm)
Tõ ph¬ng tr×nh chÝnh t¾c cña ®êng trßn ta cã t©m I(1;-2), R = 3, tõ A kÎ ®îc 2
tiÕp tuyÕn AB, AC tíi ®êng trßn vµ ACAB  => tø gi¸c ABIC lµ h×nh vu«ng c¹nh
b»ng 3 23 IA
0,5








7
5
6123
2
1
m
m
m
m
0,5
2. (1 ®iÓm)
Gäi H lµ h×nh chiÕu cña A trªn d, mÆt ph¼ng (P) ®i qua A vµ (P)//d, khi ®ã kho¶ng
çch gi÷a d vµ (P) lµ kho¶ng çch tõ H ®Õn (P).
Gi¶ sö ®iÓm I lµ h×nh chiÕu cña H lªn (P), ta cã HIAH  => HI lín nhÊt khi IA 
0,5
)5;1;7()4;1;3(  AHH VËy (P): 7(x 10) + (y 2) 5(z + 1) = 0
 7x + y -5z -77 = 0
0,5

55
C©u
VIIa
1
®iÓm
5 C çch chän 2 ch÷ sè ch½n (kÓ c¶ sè cã ch÷ sè
0 ®øng ®Çu) vµ 3
5C =10 çch chän 2 ch÷ sè lÏ => cã 2
5C . 3
5C = 100 bé 5 sè ®îc chän.
0,5
Mçi bé 5 sè nh thÕ cã 5! sè ®îc thµnh lËp => cã tÊt c¶ 2
5C . 3
5C .5! = 12000 sè.
MÆt kh¸c sè çc sè ®îc lËp nh trªn mµ cã ch÷ sè 0 ®øng ®Çu lµ 960!4.. 3
5
1
4 CC .
VËy cã tÊt c¶ 12000 960 = 11040 sè tháa m·n bµi to¸n
0,5
HƯỚNG DẪN GIẢI: (đề số 13)
I. PHẦN CHUNG:
Câu 1: :
2. Phöông trình hoaønh ñoä giao ñieåm cuûa (Cm) vaø ñöôøng thaúng y = 1 laø:
x3
+ 3x2
+ mx + 1 = 1  x(x2
+ 3x + m) = 0 

   
2
x 0
x 3x m 0 (2)
* (Cm) caét ñöôøng thaúng y = 1 taïi C(0, 1), D, E phaân bieät:
 Phöông trình (2) coù 2 nghieäm xD, xE  0.

    
      
2
m 09 4m 0
4
m0 3 0 m 0
9
Luùc ñoù tieáp tuyeán taïi D, E coù heä soá goùc laàn löôït laø:
kD = y’(xD) =     2
D D D3x 6x m (x 2m);
kE = y’(xE) =     2
E E E3x 6x m (x 2m).
Caùc tieáp tuyeán taïi D, E vuoâng goùc khi vaø chæ khi: kDkE = –1.
 (3xD + 2m)(3xE + 2m) = 9xDxE+6m(xD + xE) + 4m2
= –1
 9m + 6m (–3) + 4m2
= –1; (vì xD + xE = –3; xDxE = m theo ñònh lý Vi-ét).
 4m2
– 9m + 1 = 0  m =  
1
9 65
8
ÑS: m =      
1 1
9 65 hay m 9 65
8 8
Câu 2:
1.   3 sin x cosx 2cos3x 0  sin

3
sinx + cos

3
cosx = – cos3x.
 cos
 
  
 
x cos3x
3
 cos
 
   
 
x cos( 3x)
3

 
 
 
   

k
x
3 2 (k Z)
x k
3
 x =
 

k
3 2
(k  Z)
2. Điều kiện: x ≥ 2 và y ≥ 2 : Lấy (1) trừ (2) vế theo vế ta được:
2 2 2 2
91 91 2 2x y y x y x        
2 2
2 2
( )( )
2 291 91
x y y x
y x y x
y xx y
 
    
    
2 2
1
( ) 0
2 291 91
x y
x y x y
x yx y
 
      
      
 x = y (trong ngoặc luôn dương và x vay đều lớn hơn 2)

56
Vậy từ hệ trên ta có: 2 2
91 2x x x    2 2
91 10 2 1 9x x x       
2
2
9 3
( 3)( 3)
2 191 10
x x
x x
xx
 
    
  
2
1 1
( 3) ( 3) 1 0
2 191 10
x x
xx
  
            
 x = 3
Vậy nghiệm của hệ x = y = 3
Câu 3: J


   
 

  b
b
ln10 8x 8
2/ 3
1/33 x e 2
b e 2
e dx du 1
u
3ue 2
  
 
b 2/ 33
4 (e 2) ;
2
vôùi u = ex
– 2, du =
ex
dx)
Suy ra:
 
     
 
b 2/3
b ln2 b ln2
3 3
lim J lim 4 (e 2) (4) 6
2 2
Câu 4:
Döïng SH AB
 Ta coù:
(SAB) (ABC), (SAB) (ABC) AB, SH (SAB)   
SH (ABC)  vaø SH laø ñöôøng cao cuûa hình choùp.
 Döïng HN BC, HP AC 
 SN BC, SP AC SPH SNH      
 SHN = SHP  HN = HP.
 AHP vuoâng coù: o a 3
HP HA.sin60 .
4
 
 SHP vuoâng coù:
a 3
SH HP.tg tg
4
   
 Theå tích hình choùp
2 3
ABC
1 1 a 3 a 3 a
S.ABC : V .SH.S . .tg . tg
3 3 4 4 16
    
Câu 5: Áp dụng bất đẳng thức Cô Si, ta có:
4ab ≤ (a + b)2 1
4
a b
a b ab

 

1 1 1
( , 0)
4
a b
a b
 
    
 
Ta có:
1 1 1 1 1 1 1 1 1 1 1 1 1
2 4 2 4 2 4 8 2 2x y z x y z x y z x y z
      
             
        
Tương tự:
1 1 1 1 1
2 8 2 2x y z x y z
 
   
   
và
1 1 1 1 1
2 8 2 2x y z x y z
 
   
   
Vậy
1 1 1
2 2 2x y z x y z x y z
 
     
1 1 1 1 2009
4 4x y z
 
    
 
Vậy MaxP =
2009
4
khi x = y = z =
12
2009
II.PHẦN TỰ CHỌN:
1. Phần 1: Phần dành cho chương trình cơ bản
Câu 6a.1a
1.Giả sử AB: 5x 2y + 6 = 0; AC: 4x + 7y – 21 = 0 Vậy A(0;3)
Đường cao đỉnh BO đi qua O nhận VTCP a

= (7; 4) của AC làm VTPT
S
H
P
C
A
B
N


57
Vây BO: 7x 4y = 0 vậy B(4;7)
A n m trên Oy, v y ng cao AO chính là tr c OY, V y AC: y + 7 = 0
2. Goïi A(a; 0; 0) Ox .
 Khoaûng caùch töø A ñeán maët phaúng ( ) :
2 2 2
2a 2a
d(A; )
32 1 2
  
 
 ( ) qua 0M (1; 0; 2) vaø coù vectô chæ phöông u (1; 2; 2)

 Ñaët 0 1M M u
 
 Do ñoù: d(A; ) laø ñöôøng cao veõ töø A trong tam giaùc 0 1AM M
0 1
2
0AM M
0 1
[AM ; u]2.S 8a 24a 36
d(A; )
M M u 3
 
    
 

 Theo giaû thieát: d(A; ) = d(A; )
2
2 2 2
2
2a 8a 24a 36
4a 8a 24a 36 4a 24a 36 0
3 3
4(a 3) 0 a 3.
 
         
    
 Vaäy, coù moät ñieåm A(3; 0; 0).
Câu 6a.2a n = a bcd e
* Xem caùc soá hình thöùc a bcd e, keå caû a = 0. Coù 3 caùch choïn vò trí cho 1 (1 laø a hoaëc laø b
hoaëc laø c). Sau ñoù choïn trò khaùc nhau cho 4 vò trí coøn laïi töø X  1 : soá caùch choïn 4
7A .
Nhö theá coù 3 x (7 x 6 x 5 x 4) = 2520 soá hình thöùc thoûa yeâu caàu ñeà baøi.
* Xem caùc soá hình thöùc 0bcde .
* Loaïi nhöõng soá daïng hình thöùc 0bcde ra, ta coøn 2520 – 240 = 2280 soá n thoûa yeâu caàu ñeà
baøi.
1. Phần 2: Phần dành cho chương trình nâng cao:
Câu 6b.1b
1. (C) có tâm I(3;0) và bán kính R = 2
M  Oy  M(0;m)
Qua M kẽ hai tiếp tuyến MA và MB ( A và B là hai tiếp điểm)
Vậy


0
0
60 (1)
120 (2)
AMB
AMB
 

 
Vì MI là phân giác của AMB
(1)  AMI = 300
0
sin30
IA
MI   MI = 2R  2
9 4 7m m    
(2)  AMI = 600
0
sin60
IA
MI   MI =
2 3
3
R  2 4 3
9
3
m   Vô nghiệm
Vậy có hai điểm M1(0; 7 ) và M2(0; 7 )
2.- (d1) ñi qua ñieåm A(0; 0; 4) vaø coù vectô chæ phöông 1u (2; 1; 0)

- (d2) ñi qua ñieåm B(3; 0; 0) vaø coù vectô chæ phöông 2u (3; 3; 0) 

AB (3; 0; 4) 

 1 2 1 2AB.[u ; u ] 36 0 AB, u , u  
     
khoâng ñoàng phaúng.
 Vaäy, (d1) vaø (d2) cheùo nhau.

58
 Goïi MN laø ñöôøng vuoâng goùc chung cuûa (d1) vaø (d2)
 1M (d ) M(2t; t; 4)  , / /
2N (d ) N(3 t ; t ; 0)   
/ /
MN (3 t 2t; t t; 4)      

 Ta coù:
/ / /
1
/ /
2
MN u 2(3 t 2) (t t) 0 M(2; 1; 4)t 1
N(2; 1; 0)t 13 t 2t (t t) 0MN u
           
     
      
 
 
 Toïa ñoä trung ñieåm I cuûa MN: I(2; 1; 2), baùn kính
1
R MN 2.
2
 
 Vaäy, phöông trình maët caàu (S): 2 2 2
(x 2) (y 1) (z 2) 4.     
Câu 6b.2b
Xeùt phöông trình Z4
– Z3
+ 6Z2
– 8Z – 16 = 0
Deã daøng nhaän thaáy phöông trình coù nghieäm Z1 = –1, sau ñoù baèng caùch chia ña thöùc ta thaáy
phöông trình coù nghieäm thöù hai Z2 = 2. Vaäy phöông trình trôû thaønh:
(Z + 1)(Z – 2)(Z2
+ 8) = 0
Suy ra: Z3 = 2 2 i vaø Z4 = –2 2 i
Ñaùp soá:    1,2, 2 2 i, 2 2 i
Hết
C©u Néi dung §iÓm
 Gäi M(x;y) (C) vµ c¸ch ®Òu 2 tiÖm cËn x = 2 vµ y = 3
| x – 2 | = | y – 3 |
3x 4 x
x 2 2 x 2
x 2 x 2

      
 
 
x 1x
x 2
x 4x 2

       
VËy cã 2 ®iÓm tho¶ m·n ®Ò bµi lµ : M1( 1; 1) vµ M2(4; 6)
2
0.75®
XÐt ph¬ng tr×nh : sin6
x + cos6
x = m ( sin4
x + cos4
x ) (2)
2 23 1
1 sin 2x m 1 sin 2x
4 2
 
    
 
(1)
§Æt t = sin2
2x . Víi
2
x 0;
3
 
  
th×  t 0;1 . Khi ®ã (1) trë thµnh :
2m =
3t 4
t 2


víi  t 0;1
NhËn xÐt : víi mçi  t 0;1 ta cã :
sin 2x t
sin 2x t
sin 2x t
  
 

§Ó (2) cã 2 nghiÖm thuéc ®o¹n
2
0;
3
 
  
th×  
3 3
t ;1 t ;1
2 4
 
   

Da vµo ®å thÞ (C) ta cã : y(1)< 2m ≤ y(3/4)
7
1 2m
5
  
VËy c¸c gi¸ trÞ cÇn t×m cña m lµ :
1 7
;
2 10
 
 
0,25
0,5

59
II
2,0®
1
1,0®
sin3x sin x
sin 2x cos2x
1 cos2x

 

(1)
2cos2x.sin x
2cos 2x
42 sin x
 
   
 
§K : sinx ≠ 0 x  
 Khi  x 0;  th× sinx > 0 nªn :
(1) 2 cos2x = 2 cos 2x
4
 
 
 
x
16 2
 
  

Do  x 0;  nªn
9
x hay x
16 16
 
 
 Khi  x ;2   th× sinx < 0 nªn :
(1) 2  cos2x = 2 cos 2x
4
 
 
 
 cos -2x = cos 2x-
4
 
   
 
5
x
16 2
 
  

Do  x ;2   nªn
21 29
x hay x
16 16
 
 
0,5
0,5
2
1,0®
§Æt 3 3
u x 34, v x 3    . Ta cã :
  2 23 3
u v 1u v 1
u v u v uv 37u v 37
   
 
     
 
2
u v 1 u v 1
uv 12u v 3uv 37
   
  
   
u 3
v 4
u 4
v 3
  

 
 


Víi u = -3 , v = - 4 ta cã : x = - 61
Víi u = 4, v = 3 ta cã : x = 30
VËy Pt ®· cho cã 2 nghiÖm : x = -61 vµ x = 30
0,25
0,5
0.25
III
1.0®
1®
a)Ta cã : AB = 2 5 ,
Gäi M lµ trung ®iÓm cña BC ,
ta cã : DM = 1
SD = 2 2
SA AD 30  ,
SC = 2 2
SA AC 29 
SM = 2 2
SC CM 33 
Ta cã :
2 2 2
SD MD SM 30 1 33 1
cos SDM
2SD.MD 2 30 30
   
     (*)
Gãc  gi÷a hai ®êng th¼ng AC vµ SD lµ gãc gi÷a hai ®êng th¼ng DM
vµ SD hay  bï víi gãc  SDM . Do ®ã : cos =
1
30
b) KÎ DN // BC vµ N thuéc AC . Ta cã : BC // ( SND) . Do ®ã :
d(BC, SD) = d( BC/(SND)) = d(c/(SND))
KÎ CK vµ AH vu«ng gãc víi SN , H vµ K thuéc ®êng th¼ng SN
Ta cã : DN // BC  DN AC 1 
Vµ    SA ABC SA DN 2  
Tõ (1) vµ (2) suy ra : DN  ( SAC)  DN KC 3 
Do c¸ch dùng vµ (3) ta cã : CK  (SND) hay CK lµ kho¶ng c¸ch tõ C
0.5
N M
D
S
A B
C
K

60
®Õn mp(SND)
MÆt kh¸c : ΔANH = ΔCNK nªn AH = CK
Mµ trong tam gi¸c vu«ng SAN l¹i cã :
2 2 2
1 1 1 1 5
1 AH
AH SA AN 25 26
     
VËy kho¶ng c¸ch gi÷a BC vµ SD lµ : CK =
5
26
0,5
IV
2®
1
1.0®
Ta cã : sinx – cosx + 1 = A(sinx + 2cosx + 3) + B(cosx – sinx) + C
= (A – 2B) sinx + ( 2A + B) cosx + 3A + C
1
A
5A 2B 1
3
2A B 1 B
5
3A C 1
8
C
5

 
  
 
       
   


VËy I =
 2 2 2
0 0 0
d sin x 2cosx 31 3 8 dx
dx
5 5 sin x 2cosx 3 5 sin x 2cosx 3
  
 
  
     
I =   22
0 0
1 3 8
x ln sin x 2cosx 3 J
5 5 5

      
I =  
3 8
ln 4 ln 5 J
10 5 5

   
TÝnh J =
2
0
dx
sin x 2cosx 3

  .
§Æt t = tan
x
2
2
2
1 x 2tdt
dt tan 1 dx
2 2 t 1
 
     
 
§æi cËn : Khi x =
2

th× t = 1
Khi x = 0 th× t = 0
VËy
 
1 1 1
2
2 22 2
0 0 0
2 2
2dt
dt dtt 1J 2 2
2t 1 t t 2t 5 t 1 22 3
t 1 t 1
  
     
 
  
L¹i ®Æt t = 1 = 2 tan u . suy ra dt = 2 ( tan2
u + 1)du
§æi cËn khi t = 1 th× u =
4

Khi t = 0 th× u =  víi tan
1
2
 
 
 
24
4
2
2 tan u 1 du
J u
44 tan u 1




 
    

Do ®ã : I =
3 3 5 8
ln
10 5 4 5

  
0,25
0,25
0.5
2a
0.5®
G/s sè phøc z cã d¹ng : z = x + iy víi x,y  , | z | = 2 2
x y
Ta cã : | z | = 1 + ( z – 2 ) i
 2 2
x y = ( 1 – y ) + ( x – 2 ) i 0,5

61
 
22 2
x 2 0 x 2
1 y 0 3
y
2x y 1 y
    
   
    
0.5
2b
0.5đ
G/s sè phøc z cã d¹ng : z = x + iy víi x,y  ,
Ta cã : | z - i | = | x + ( y - 1)i | =  
22
x y 1 
Do ®ã : 1 < | z - i | < 2  1 < | z - i |2
< 4
 
22
1 x y 1 4    
Gäi (C1) , (C2) lµ hai ®êng trßn ®ång t©m I( 0 ; 1) vµ cã b¸n kÝnh lÇn
lît lµ : R1=1 , R2 = 2 . VËy tËp hîp c¸c ®iÓm cÇn t×m lµ phÇn n»m gi÷a
hai ®êng trßn (C1) vµ (C2)
Va
3®
1
+) PT c¹nh BC ®i qua B(2 ; -1) vµ nhËn VTCP  1u 4;3

cña (d2) lµm
VTPT
(BC) : 4( x- 2) + 3( y +1) = 0 hay 4x + 3y - 5 =0
+) Täa ®é ®iÓm C lµ nghiÖm cña HPT :
 
4x 3y 5 0 x 1
C 1;3
x 2y 5 0 y 3
     
    
    
+) §êng th¼ng ∆ ®i qua B vµ vu«ng gãc víi (d2) cã VTPT lµ
 2u 2; 1 

∆ cã PT : 2( x - 2) - ( y + 1) = 0 hay 2x - y - 5 = 0
+) Täa ®é giao ®iÓm H cña ∆ vµ (d2) lµ nghiÖm cña HPT :
 
2x y 5 0 x 3
H 3;1
x 2y 5 0 y 1
    
   
    
+) Gäi B’ lµ ®iÓm ®èi xøng víi B qua (d2) th× B’ thuéc AC vµ H lµ trung
®iÓm cña BB’ nªn :
 B' H B
B' H B
x 2x x 4
B' 4;3
y 2y y 3
  
 
  
+) §êng th¼ng AC ®i qua C( -1 ; 3) vµ B’(4 ; 3) nªn cã PT : y - 3 = 0
+) Täa ®é ®iÓm A lµ nghiÖm cña HPT :
y 3 0 x 5
A ( 5;3)
3x 4y 27 0 y 3
    
    
    
+) §êng th¼ng qua AB cã VTCP  AB 7; 4 

, nªn cã PT :
x 2 y 1
4x 7y 1 0
7 4
 
    

0,25
0,5
0,25
2a
§êng th¼ng (d1) ®i qua M1( 1; -4; 3) vµ cã VTCP  1u 0;2;1

§êng th¼ng (d2) ®i qua M2( 0; 3;-2) vµ cã VTCP  2u 3;2;0 

Do ®ã :  1 2M M 1;7; 5  

vµ  1 2u ,u 2; 3;6     
 
Suy ra 1 2 1 2u ,u .M M 49 0     
  
. VËy (d1) vµ (d2) chÐo nhau
0.5
2b
LÊy A( 1; -4 + 2t; 3 + t) thuéc (d1) vµ B(-3u; 3 + 2u; -2) thuéc (d2) .Ta cã
:
 AB 3u 1;7 2u 2t; 5 t      

A,B lµ giao ®iÓm cña ®êng vu«ng gãc chung cña (d1) vµ (d2) víi hai
®êng ®ã 1
2
AB.u 0 14 4u 4t 5 t 0 u 1
9u 3 14 4u 4u 0 t 1AB.u 0
         
    
       
 
 

62
Suy ra : A( 1; -2; 4) vµ B(3; 1; -2)  AB 2;3; 6  

 AB = 7
Trung ®iÓm I cña AB cã täa ®é lµ : ( 2; -
1
2
; 1)
MÆt cÇu (S) cÇn t×m cã t©m I vµ b¸n kÝnh lµ AB/2 vµ cã PT :
   
2
2 21 49
x 2 y z 1
2 4
 
      
 
0,5
3 Sè çch lÊy 2 bi bÊt k× tõ hai hép bi lµ : 52.25 = 1300
Sè çch lÊy ®Ó 2 viªn bi lÊy ra cïng mµu lµ : 30x10+7x6+15x9 = 477
X¸c suÊt ®Ó 2 bi lÊy ra cïng mµu lµ :
477
1300
0.5
0.5
Vb
3.0 ®
1
+) Täa ®é ®iÓm B lµ nghiÖm cña HPT :
 
x 13x y 3 0
B 1;0
y 0y 0
   
  
 
Ta nhËn thÊy ®êng th¼ng BC cã hÖ sè gãc
k = 3 , nªn 0
ABC 60  . Suy ra
®êng ph©n gi¸c trong gãc B cña
ΔABC cã hÖ sè gãc k’ =
3
3
nªn cã PT :
3 3
y x
3 3
  (Δ)
T©m I( a ;b) cña ®êng trßn néi tiÕp tam gi¸c ABC thuéc (Δ) vµ çch
trôc Ox mét kho¶ng b»ng 2 nªn : | b | = 2
+ Víi b = 2 : ta cã a = 1 2 3 , suy ra I=( 1 2 3 ; 2 )
+ Víi b = -2 ta cã a = 1 2 3 , suy ra I = ( 1 2 3 ; -2)
 §êng ph©n gi¸c trong gãc A cã d¹ng:y = -x + m (Δ’).V× nã ®i qua I
nªn
+ NÕu I=( 1 2 3 ; 2 ) th× m = 3 + 2 3 .
Suy ra : (Δ’) : y = x + 3 + 2 3 . Khi ®ã (Δ’) c¾t Ox ë A(3 + 2 3 . ; 0)
Do AC vu«ng gãc víi Ox nªn cã PT : x = 3 + 2 3 .
Tõ ®ã suy ra täa ®é ®iÓm C = (3 + 2 3 ; 6 + 2 3 )
VËy täa ®é träng t©m G cña tam gi¸c ABC lóc nµy lµ :
4 4 3 6 2 3
;
3 3
  
  
 
.
+ NÕu I=( 1 2 3 ; 2 ) th× m = -1 - 2 3 .
Suy ra : (Δ’) : y = x 1 2 3 . Khi ®ã (Δ’) c¾t Ox ë A(-1 - 2 3 . ; 0)
Do AC vu«ng gãc víi Ox nªn cã PT : x = -1 - 2 3 .
Tõ ®ã suy ra täa ®é ®iÓm C = (-1 - 2 3 ; -6 - 2 3 )
VËy täa ®é träng t©m G cña tam gi¸c ABC lóc nµy lµ :
1 4 3 6 2 3
;
3 3
   
  
 
.
VËy cã hai tam gi¸c ABC tho¶ m·n ®Ò bµi vµ träng t©m cña nã lµ :
G1 =
4 4 3 6 2 3
;
3 3
  
  
 
vµ G2 =
1 4 3 6 2 3
;
3 3
   
  
 
0.25
0.5
0,25
2a
+ §êng th¼ng (d) ®i qua M(0; -1; 0) vµ cã VTCP  du 1;0; 1 

+ Mp (P) cã VTPT :  Pn 1;2;2

O
y
xA
B
C
60

63
I.PhÇn dµnh cho tÊt c¶ çc thÝ sÝnh
C©uI §¸p ¸n §iÓm
2. (0,75 ®iÓm)
Hoµnh ®é giao ®iÓm cña ®å thÞ (C ) vµ ®êng th¼ng d lµ nghiÖm cña
ph¬ng tr×nh








)1(021)4(
2
2
12
2
mxmx
x
mx
x
x
Do (1) cã mmmvam  0321)2).(4()2(01 22
nªn
®êng th¼ng d lu«n lu«n c¾t ®å thÞ (C ) t¹i hai ®iÓm ph©n biÖt A, B
0,25
Ta cã yA = m – xA; yB = m – xB nªn AB2
= (xA – xB)2
+ (yA – yB)2
= 2(m2
+
12) suy ra AB ng¾n nhÊt  AB2
nhá nhÊt  m = 0. Khi ®ã 24AB
0,5
II
(2
®iÓm)
1. (1 ®iÓm)
Ph¬ng tr×nh ®· cho t¬ng ®¬ng víi
9sinx + 6cosx – 6sinx.cosx + 1 – 2sin2
x = 8
 6cosx(1 – sinx) – (2sin2
x – 9sinx + 7) = 0
 6cosx(1 – sinx) – (sinx – 1)(2sinx – 7) = 0
0,5
 (1-sinx)(6cosx + 2sinx – 7) = 0
 




)(07sin2cos6
0sin1
VNxx
x
0,25
 

2
2
kx 
0,25
2. (1 ®iÓm)
§K:





03loglog
0
2
2
2
2 xx
x
BÊt ph¬ng tr×nh ®· cho t¬ng ®¬ng víi 0,5
Mp (R) chøa (d) vµ vu«ng gãc víi (P) cã VTPT :
 R d Pn u ;n 2; 3;2    
  
Thay x, y, z tõ Pt cña (d) vµo PT cña (P) ta cã :
t - 2 - 2t + 3 = 0 hay t =1 . Suy ra (d) c¾t (P) t¹i K(1; -1; -1)
H×nh chiÕu (d’) cña (d) trªn (P) ®i qua K vµ cã VTCP :
 d' R Pu n ;n 10;2; 7    
  
VËy (d’) cã PTCT :
x 1 y 1 z 1
10 2 7
  
 

0,25
0,25
2b
LÊy I(t; -1; -t) thuéc (d) , ta cã :
d1 = d(I, (P)) =
1 t
3

; d2 = d(I, (Q)) =
5 t
3

Do mÆt cÇu t©m I tiÕp xóc víi (P0 vµ (Q) nªn : R = d1 = d2
 | 1 - t | = | 5 - t |  t = 3
Suy ra : R = 2/3 vµ I = ( 3; -1; -3 ) . Do ®ã mÆt cÇu cÇn t×m cã PT lµ :
     
2 2 2 4
x 3 y 1 z 3
9
     
0,25
0,25
3. sai
Sè çch chän 5 qu©n bµi trong bé bµi tó l¬ kh¬ lµ : 52
5C 2598960
Sè çch chän 5 qu©n bµi trong bé bµi tó l¬ kh¬ mµ trong 5 qu©n bµi ®ã
cã ®óng 3 qu©n bµi thuéc 1 bé lµ : 13. 4
3C 52
X¸c suÊt ®Ó chän 5 qu©n bµi trong bé bµi tó l¬ kh¬ mµ trong 5 qu©n bµi
®ã cã ®óng 3 qu©n bµi thuéc 1 bé lµ :
52
2598960
=
13
649740
0.5
0.5

64
)1()3(log53loglog 2
2
2
2
2  xxx
®Æt t = log2x,
BPT (1)  )3(5)1)(3()3(5322
 tttttt























4log3
1log
43
1
)3(5)3)(1(
3
1
2
2
2
x
x
t
t
ttt
t
t 0,25







168
2
1
0
x
x
VËy BPT ®· cho cã tËp nghiÖm lµ: )16;8(]
2
1
;0( 
III
1 ®iÓm  
xx
dx
xxx
dx
I 23233
cos.2sin
8
cos.cos.sin
®Æt tanx = t
dt
t
t
t
t
dt
I
t
t
x
x
dx
dt
 






3
32
3
2
22
)1(
)
1
2
(
8
1
2
2sin;
cos
0,5
C
x
xxxdtt
t
tt
dt
t
ttt






2
2433
3
246
tan2
1
tanln3tan
2
3
tan
4
1
)
3
3(
133
0,5
C©u IV
1 ®iÓm
Do )( 111 CBAAH  nªn gãc HAA1 lµ gãc gi÷a AA1 vµ (A1B1C1), theo gi¶
thiÕt th× gãc HAA1 b»ng 300
. XÐt tam gi¸c vu«ng AHA1 cã AA1 = a, gãc
HAA1 =300
2
3
1
a
HA  . Do tam gi¸c A1B1C1 lµ tam gi¸c ®Òu c¹nh a,
H thuéc B1C1 vµ
2
3
1
a
HA  nªn A1H vu«ng gãc víi B1C1. MÆt kh¸c
11CBAH  nªn )( 111 HAACB  0,5
KÎ ®êng cao HK cña tam gi¸c AA1H th× HK chÝnh lµ kho¶ng c¸ch gi÷a
AA1 vµ B1C1
0,25
Ta cã AA1.HK = A1H.AH
4
3.
1
1 a
AA
AHHA
HK 
0,25
A1
A B
C
C
B1
K
H

65
C©u V
1 ®iÓm
¸p dông bÊt ®¼ng thøc C« si cho 2005 sè 1 vµ 4 sè a2009
ta cã
.2009....20091...11 2009 20092009200920092009200920092009
2005
aaaaaaaa  
T¬ng tù ta cã
.2009....20091...11 2009 20092009200920092009200920092009
2005
bbbbbbbbb  
.2009....20091...11 2009 20092009200920092009200920092009
2005
ccccccccc  
0,5
Céng theo vÕ (1), (2), (3) ta ®îc
)(20096027
)(2009)(46015
444
444200920092009
cba
cbacba


Tõ ®ã suy ra 3444
 cbaP
MÆt kh¸c t¹i a = b = c = 1 th× P = 3 nªn gi¸ trÞ lín nhÊt cña P = 3.
0,5
C©u
VIa
2
®iÓm
1.Tõ ph¬ng tr×nh chÝnh t¾c cña ®êng trßn ta cã t©m I(1;-2), R = 3, tõ A kÎ
®îc 2 tiÕp tuyÕn AB, AC tíi ®êng trßn vµ ACAB  => tø gi¸c ABIC lµ h×nh
vu«ng c¹nh b»ng 3 23 IA
0,5








7
5
6123
2
1
m
m
m
m
0,5
2. (1 ®iÓm)
Gäi H lµ h×nh chiÕu cña A trªn d, mÆt ph¼ng (P) ®i qua A vµ (P)//d, khi ®ã
G.sö ®iÓm I lµ h×nh chiÕu cña H lªn (P), ta cã HIAH  => HI lín nhÊt khi IA 
0,5
)5;1;7()4;1;3(  AHH VËy (P): 7(x – 10) + (y – 2) – 5(z + 1) = 0
 7x + y -5z -77 = 0
0,5
C©u
VIIa
1
®iÓm
4 C c¸ch chän 2 ch÷ sè ch½n (v× kh«ng cã sè
0)vµ 102
5 C c¸ch chän 2 ch÷ sè lÏ => cã 2
5C . 2
5C = 60 bé 4 sè tháa m·n bµi to¸n
0,5
Mçi bé 4 sè nh thÕ cã 4! sè ®îc thµnh lËp. VËy cã tÊt c¶ 2
4C . 2
5C .4! = 1440 sè 0,5
2.Ban n©ng cao.
C©u
VIa
2
®iÓm
1.( 1 ®iÓm)
Tõ ph¬ng tr×nh chÝnh t¾c cña ®êng trßn ta cã t©m I(1;-2), R = 3, tõ A kÎ ®îc 2
tiÕp tuyÕn AB, AC tíi ®êng trßn vµ ACAB  => tø gi¸c ABIC lµ h×nh vu«ng c¹nh
b»ng 3 23 IA
0,5








7
5
6123
2
1
m
m
m
m
0,5

66
2.Gäi H lµ h×nh chiÕu cña A trªn d, mÆt ph¼ng (P) ®i qua A vµ (P)//d, khi ®ã
Gi¶ sö ®iÓm I lµ h×nh chiÕu cña H lªn (P), ta cã HIAH  => HI lín nhÊt khi IA 
0,5
)5;1;7()4;1;3(  AHH VËy (P): 7(x – 10) + (y – 2) – 5(z + 1) = 0
 7x + y -5z -77 = 0
0,5
C©u
VIIa
1
®iÓm
5 C çch chän 2 ch÷ sè ch½n (kÓ c¶ sè cã ch÷ sè
0 ®øng ®Çu) vµ 3
5C =10 çch chän 2 ch÷ sè lÏ => cã 2
5C . 3
5C = 100 bé 5 sè ®îc chän.
0,5
Mçi bé 5 sè nh thÕ cã 5! sè ®îc thµnh lËp => cã tÊt c¶ 2
5C . 3
5C .5! = 12000 sè.
MÆt kh¸c sè çc sè ®îc lËp nh trªn mµ cã ch÷ sè 0 ®øng ®Çu lµ 960!4.. 3
5
1
4 CC .
VËy cã tÊt c¶ 12000 – 960 = 11040 sè tháa m·n bµi to¸n
0,5
I 2.5
b Tìm M  (C) để tổng các khoảng cách đến 2 tiệm cận nhỏ nhất 0,75

4 4
1 .
1
y x Y X
x X
      

Với





yY
xX 1
0.25
TCĐ d: X = 0, TCX d’: X Y = 0 ⇒ T = d(M, d) + d(M, d’) =
4 7| | 4 4
| | | | 2
2 | | 2 2
X Y
X X
X

     Dấu "=" xảy ra
⇔
4
| |
| | 2
X
X
  4 42 3 34
2 1 2
2
X X x      
0.5
 Gọi M(2; m)  d1: x = 2. Khi đó đt d  M
 d: y = k(x 2) + m. Để đt d tiếp xúc với
(C’)  hệ:
 





kxx
mxkxxx
9123
2196
2
23
có nghiệm
0,25
 2x3
12.x2
+ 24x 17 + m = 0 (1) có nghiệm.
 Số tiếp tuyến kẻ từ M đến (C’) là số nghiệm của Pt (1)
 Xét hàm số y = 2x3
12.x2
+ 24x 17 + m
 y’ = 6(x2)2
 0 x  Hàm luôn đồng biến  Pt (1) luôn có
nghiệm duy nhất  từ một điểm trên đt x = 2 luôn kẻ được một tiếp
tuyến đến đồ thị (C’).
0,5
II 1,5
1 Giải phương trình: 0,75
 
      015.3315.315.35
3510325.3
2222
22




xxxx
xx
x
xx
0.25

67
  
 
 










2035
1015.3
03515.3
2
2
22
x
x
x
x
xx
  3log2
3
1
log2
3
1
51 55
2
 
xx
0.25
  352 2
 
xx
Vế trái là hàm đồng biến vế phải là hàm nghịch biến mà (2) có nghiệm
x = 2 nên là nghiệm duy nhất.
Vậy Pt có nghiệm là: x = 3log2 5 và x = 2
0.25
2 Giải hệ phương trình: 0,75
    






22cossincossin
2coscos
2sinsin
yyxx
yx
yx
0.25


















































2
4
2
4
1
4
cos
1
4
cos
2
4
cos
4
cos
ly
kx
y
x
yx
0.25
Thử lại thấy đúng nên:












2
4
2
4
ly
kx
là nghiệm của hệ phương trình. 0.25
III 1,5
1 Giải phương trình: . 0,5
    02coscoslogsincoslog 1  xxxx
x
x
Điều kiện:








02coscos
0sincos
10
xx
xx
x
.
Khi đó Pt 






2
cos2cossin2cos

xxxx
0.25


















3
2
6
2
2
2
2
2
2
2
2







k
x
kx
kxx
kxx
.
Kết hợp với điều kiện ta được:
3
2
6
 k
x  (Với k ∊ N*).
0.25
2 Giải bất phương trình: 0,5

68
      02301311 232323
 xxxxxxxx
0232
 tt Đặt
3
2
1  xxt
0.25
2
3 2 2
1 1
1 3 3
2
t
t x x x
t
t

 

            
  
0.25
3 0,5
. Trong 10 chữ số từ 0 đến 9 có tât cả 5
10C tập con gồm 5 chữ
số khác nhau.
0,25
Trong mỗi tập con này chỉ có duy nhất một cách sắp xếp số có 5
chữ số mà chữ số đứng trước lớn hơn chữ số đứng liền sau. Vậy có tất
cả 5
10C = 252 số.
0,25
IV 2.0
1 Xác định tọa độ điểm C  (P) sao cho ABC đều 1.0
Để ABC là tam giác đều  đường cao MC = AB 62/3 
Gọi M là trung điểm của AB  M(1; 0; 2).
Gọi (Q) là mf đi qua M và vuông góc với AB
 (Q): x + z + 1 = 0
0,25
Gọi d = (P) n (Q) 














tz
ty
tx
zx
zyx
d
21
22
01
01783
:
 C  d  C(2 2t; t; 1 + 2t)
0,25
     
 
2 22
2 2
1 2
1 2
3 2 ; ;3 2 6 3 2 3 2 6
9 24 12 0 3 8 4 0 2; 2/3
2 2 1
2; 2; 3 , ; ;
3 3 3
MC t t t MC t t t
t t t t t t
C C
            
            
 
      
 

0,25

69
0.25
2 Xác định các góc hợp bởi các cạnh đối diện của tứ diện. 1.0
Lấy E, F, G lần lượt là trung điểm của AB, CD, AC ta có:
GE = GF = c/2. ∆ACD = ∆BCD (c.c.c) ⇒ FA = FB
⇒
4
22
4
22 222222
22 acbCDADAC
FBFA




0.25
FE là trung tuyến của ∆FAB nên:



4
22 222
2 ABFBFA
FE
2
222
acb  0.25
Gọi là góc tạo bởi AD và BC ta có :
 
2
22
|
.2
||
|,cos|cos 2
2222
222
c
acbc
GFGE
FEGFGE
GFGE





2
22
||
c
ba 
 . Vậy 2
22
||
cos
c
ba 

0.25
Tương tự nếu gọi lần lượt là góc tạo bởi CD, AB và
DB, AC ta có: 2
22
||
cos
a
cb 
 , 2
22
||
cos
b
ac 
 0.25
P
Q
A
B
M
C1
C2

70
3 0,5
. Trong 10 chữ số từ 0 đến 9 có tât cả 5
9C tập con gồm 5 chữ
số khác nhau.
0,25
Trong mỗi tập con này chỉ có duy nhất một cách sắp xếp số có 5
chữ số mà chữ số đứng trước lớn hơn chữ số đứng liền sau. Vậy có tất
cả 5
9C = 126 số.
0,25
V 2,5
1 0,5
Đặt:
3 2
cos 1
cos 2.cos
u x du dx
d x
dv v
x x
  
 
 
    
0,25
/ 4
/ 44
0 02 2
0
1 1 1
2cos 2 cos 4 2 4 2
x dx
I tgx
x x

 
       0,25
2 1,0
1
2
0
2 2J x x x dx   . Đặt: x 1 = tgt
2
2
1
; 2 2
cos cos
dt
dx x x
t t
   
0 0 0
3 4 3
4 4 4
1 sin
cos cos cos
tgt t dt
J dt dt
t t t  
  

     
0,25
 
   
 
   
0
1 13
4
20 0sin
1 2 2 2 2
1 1
2 2
1 1
1 2 2
3cos 3
1 11
41 1 1 1
t u
J J
t
u udu
J du
u u u u



 
    
  
  
   
 
0,25
F
E
G
B D
A
C

71
      
0 0 0
2 2
1 1 1
2 2 2
1
. 2
4 1 11 1
du du du
u uu u  
 
 
     
 
   0,25
  
0 0
22 2
2 2
1 1 1 1 1 1
2ln 2ln
4 1 1 1 4 1 1
1 2 1 1
2 2ln 2 4ln 2 1 .
4 42 1
u u u
u u u u u 
     
              
 
     
 
0,25
3 1,0
.
2
111
222
abc
cba
abcacbbca







Ta có:
abcabc
abcabc
cabcab
cabcab
bcabca
bcabca
2
11
2
2
11
2
2
11
2
2
2
2
2
2
2









0.5
2 2 2
1 1 1 1 1 1
2 2 2
1 2 2 2.
2 2 2
a bc b ca c ab a bc b ca b ca
b c c a a b
bc ca ab a b c
abc abc abc
     
  
  
    
  
Dấu “=” xảy ra khi và chỉ khi a = b = c.
0.5
LỜI GIẢI TÓM TẮT:
I. PHẦN CHUNG:
Câu 1:
1. Bạn đọc tự giải.
2. MN

= (2;1). ==> MN: x + 2y + 3 = 0
Đường thẳng (d)  MN, (d) có dạng phương trình y = 2x + m.
Gọi A, B là hai điểm thuộc (C) đối xứng nhau qua đường thẳng MN
Hoành độ của A và B là nghiệm của phương trình:
2 4
2
1
x
x m
x

 

 2x2
+ mx + m + 4 = 0 ( x ≠ 1) (1)
Để (d) cắt (C) tại hai điểm phân biệt khi và chỉ khi (1) có  = m2 – 8m – 32 > 0
Ta có A(x1,2x1 + m), B(x2;2x2 + m) với x1, x2 là nghiệm của (1)
Trung điểm của AB là I 1 2
1 2;
2
x x
x x m
 
  
 
 I(( ; )
4 2
m m
 ( theo định lý Viet)
Ta có I  MN ==> m = 4, (1)  2x2
– 4x = 0
 A(0; 4), B(2;0)
Câu 2:
1. 4cos4
x – cos2x
1 3x
os4x +cos
2 4
c =
7
2

72
 (1 + cos2x)2
– cos2x 21 3x
(2 os 2 1)+cos
2 4
c x  =
7
2
 cos2x +
3x
os
4
c = 2

os2x = 1
3x
cos 1
4
c



( vì VT ≤ 2 với mọi x)
 ( ; )8
3
x k
k mm
x






  x = 8n (n)
2. Ta thấy phương trình: 3x
.2x = 3x
+ 2x + 1 (2) có hai nghiệm x =  1.
Ta có x =
1
2
không là nghiệm của phương trình nên
(2)
2 1
3
2 1
x x
x

 

Ta có hàm số y = 3x
tăng trên R
hàm số y =
2 1
2 1
x
x


luôn giảm trên mỗi khoảng
1 1
; , ;
2 2
   
    
   
Vậy Phương trình (2) chỉ có hai nghiệm x =  1
Câu 3:
Ta có
2 2
1 2sin os
1 sinx 12 2 tan
1+cosx 22 os 2 os
2 2
x x
c
x
x x
c c


  
Vậy: K =
2 2
20 0
tan
22 os
2
x
xe dx x
e dx
x
c
 
  = M + N
Với M =
2
20 2 os
2
x
e dx
x
c

 Dùng phương pháp tptp
Đặt
2
'
1
'
tan
2 os 2
2
x
xu e
u e
xv
vx
c
 
  
 
 

Vậy M = tan 2
2
0
x x
e

N = 2
e

N ==> K = 2
e

Câu 4:
Gọi O là tâm đường tròn ngoại tiếp tam giác ABC, M là trung
điểm của BC, theo tính chất của hình chóp đều AMS 
Gọi I là tâm của mặt cầu nội tiếp hình chóp, I  SO; N là hình
chiếu của I trên SM, MI là phân giác của AMS 
Ta có SO = OM tan =
3
6
a
tan ( Với a là độ dài của cạnh đáy)
Ta có SO2
+ OM2
= SB2
– BM2
2 2 2
2
tan 1
12 12 4
a a a
   
2
2 3
4 tan
a

 


73
r = OI = OM.tan
2

=
2
tan
2
4 tan




Vậy V =
 
3
32
4 tan
2
3 4 tan



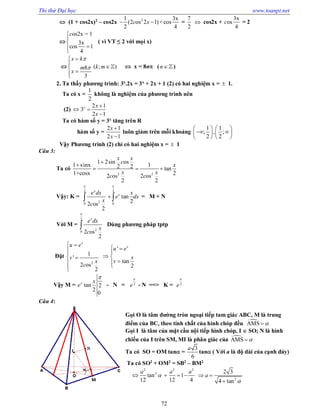
Câu 5:
Ta có (6; 4;4)AB  

==> AB//(d)
Gọi H là hình chiếu của A trên (d)
Gọi (P) là mặt phẳng qua A và (P)  (d) ==> (P): 3x – 2y + 2z + 3 = 0
H = (d) (P) ==> H( 1;2;2)
Gọi A’ là điểm đối xứng của A qua (d) ==> H là trung điểm của AA’ ==> A’(3;2;5)
Ta có A;A’;B;(d) cùng nằm trong một mặt phẳng. Gọi M = A’B(d)
Lập phương trình đường thẳng A’B ==> M(2;0;4)
II. PHẦN RIÊNG:
1) Theo cương trình chuẩn:
Câu 6a:
1. Gọi A là biến cố: “ba đoạn thẳng lấy ra lập thành một tam giác”
Các khả năng chọn được ba đoạn thẳng lập thành một tam giác
{4;6;8}, {4;8;10}, {6;8;10}
Vậy: n() = 3
5 10C  ; n(A) = 3 ==> P(A) =
3
10
2.
8
5
x x y x y y
x y
   

 

( 1) ( 8)
5
x x y y
y x
   

 
2 2
0
0
( 1) ( 8)
5
x
y
x x y y
y x

 
 
  
  
 2
1
0
3 22 45 0
5
x
y
x x
y x

 

  
  

9
4
x
y



Câu 7a:
Trên nửa khoảmg 0;
3
 
  
, cosx ≠ 0 chia tử và mẫu của hàm số cho cos3
x ta được
y =
2
2 3
1 tan
2tan tan
x
x x


Đặt t = tanx ==> t (0; 3]
Khảo sát hàm số y =
2
2 3
1
2
t
t t


trên nửa khoảng 0;
3
 
  
y’ =
4 2
2 3 2
3 4
(2 )
t t t
t t
 

; y’ = 0
0
1
x
x

  

74
Vậy giá trị nhỏ nhất của hàm số bằng 2 khi x =
4

2) Theo chương trình nâng cao:
Câu 6b:
1. Điều kiện: n nguyên dương và n ≥ 3
Ta có 1 3 2
2n n nC C C  
! ! !
2
1!( 1)! 3!( 3)! 2!( 2)!
n n n
n n n
  
  
 n2
– 9n + 14 = 0  n = 7
Ta có số hạng thứ 6 :    
2 5
55 lg(10 3 ) ( 2)lg3
7 2 2
x
x
C  
= 21  21.2
lg(10 3 )x

2(x – 2)lg3
= 21
 lg(10 – 3x
) + lg3(x – 2)
= 0  (10 – 3x
)3x – 2
= 1  32x
10.3x
+ 9 = 0
0
2
x
x

  
2. Gọi β = r( cos + isin)  β3
= r3
( cos3 + isin3)
Ta có: r3
( cos3 + isin3) =
2 2
3 os in
3 3
c s
  
 
 
3
3r 
 

3
3
2 2
9 3
r
k 

 

 
 

Suy ra β
Câu 7b:
Theo tính chất ba cạnh của một tam giác, ta có độ dài mỗi cạnh nhỏ hơn 1 ( vì a + b + c = 2).
Áp dụng bất đẳng thức CôSi cho ba số dương: 1 – a, 1 – b, 1 – c
3 – (a + b + c) 33 (1 )(1 )(1 )a b c    > 0
1
(1 )(1 )(1 ) 0
27
a b c     
28
1
27
ab bc ca abc     
56
2 2 2 2 2
27
ab bc ca abc     
2 2 2 2 56
2 ( ) ( 2 )
27
a b c a b c abc         2 2 252
2 2
27
a b c abc     
Dấu đẳng thức xảy ra khi a = b = c =
2
3
Lời giải tóm tắt(Đề 18)
Câu I:
2.
Đồ thị hàm số cắt trục hoành tại 3 điểm phân biệt có hoành độ lập thành cấp số cộng
 Phương trình 3 2
3 9 0   x x x m có 3 nghiệm phân biệt lập thành cấp số cộng
 Phương trình 3 2
3 9x x x m    có 3 nghiệm phân biệt lập thành cấp số cộng
 Đường thẳng y m  đi qua điểm uốn của đồ thị
.11 11m m     

75
Câu II:
1.
   
 
cos sin
cos
cos
cos cos
cos cos
cos cos cos
cos cos cos
cos cos cos
2 2
2 3
2 3
2
1 1
4 3 2 2
2
1
1 13
4 2 4
2
1 2 2 1
3
2 2 2 3
3
2 2 2 1 4 3
2 4 2 4 3 0
4 4 3 0
x x
x
x
x
x
x
a a a
a a a
a a a
a a a
 


  
    
 
     
 
     
     
   

76
 
cos
cos
cos
.cos cos
cos
0
30
31 3 3 2
2
2
62
3 3 3 3 3
loaïi
2
a x x
k
x k
a
x x
x kk
a



 
 

   
            
              

2.
)4(log3)1(log
4
1
)3(log
2
1
8
8
42
xxx  .
Điều kiện:
.
3
1 0 1
0
x
x x
x
 

   
 
Biến đổi theo logarit cơ số 2 thành phương trình
    
 
log log
.
2 2
2
3 1 4
2 3 0
1 loaïi
3
3
x x x
x x
x
x
x
    
   
 
  

Câu III:
 

4
6
2
cos1cos
tan


dx
xx
x
I
tan tan
cos tancos
cos
4 4
2 2
2
26 6
1 21
x x
dx dx
x xx
x
 
 
 

  .
Đặt tan .
cos2
1
u x du dx
x
   .
1
6 3
1
4
x u
x u


  
  
.
1
2
1
3
2
u
I dx
u
 


Đặt 2
2
2
2
u
t u dt du
u
   

.
1 7
33
u t  
.1 3u t  
.
3
3
7
7 3
3
7 3 7
3
3 3
I dt t

     

77
Câu IV:
ñaùyV S h  .
2
ñaùy
3
2
a
S  ,
6
3
a
h 
.
3
3
2
a
V 
Câu V:
mxxx  12213 232
( Rm  ).
Đặt   2 3 2
3 1 2 2 1f x x x x     , suy ra  f x xác định và liên tục trên đoạn ;
1
1
2
 
  
.
 '
2
2 3 2 2 3 2
3 3 4 3 3 4
1 2 1 1 2 1
x x x x
f x x
x x x x x x
  
      
      
.
;
1
1
2
x
 
    
ta có
2 3 2
4 3 3 4
3 4 0 0
3 1 2 1
x
x x
x x x

       
  
.
Vậy:
 ' 0 0f x x   .
Bảng biến thiên:
 
 
' || ||
1
0 1
2
0
1
CÑ
3 3 22
2
4
x
f x
f x

 


Dựa vào bảng biến thiên, ta có:
Phương trình đã cho có 1 nghiệm duy nhất thuộc ;
1
1
2
 
  
3 3 22
4
2
m

    hoặc 1m  .
Câu VI:
1.
Phương trình đường trung trực của AB là 3 6 0x y   .
Tọa độ tâm I của đường tròn là nghiệm của hệ:
 ; .
2 5 1
1 3
3 6 3
x y x
I
x y y
   
   
    
5R IA  .
Phương trình đường tròn là    
2 2
1 3 25x y    .
2.
a.
 , ,M x y z sao cho 2 2
5MA MB 

78
         
.
2 2 2 2 22
1 1 2 2 2 5
2 2 7 0
x y z x y z
x y
           
   
Vậy quỹ tích các điểm M là mặt phẳng có phương trình 2 2 7 0x y   .
b.
   , ; ; ; ;2 2 2 2 1 1 1OA OB      
 
 : 0OAB x y z    .
 : 0Oxy z  .
 ; ;N x y z cách đều  OAB và  Oxy      , ,d N OAB d N Oxy 
13
x y z z 
 
 
  .
3 1 0
3
3 1 0
x y z
x y z z
x y z
    
     
    
Vậy tập hợp các điểm N là hai mặt phẳng có phương trình  3 1 0x y z    và
 3 1 0x y z    .
Câu VII:
Khai triển  1
n
x ta có:
  ... .0 1 2 2 3 3 1 1
1
n n n n n
n n n n n nx C C x C x C x C x C x 
       
Nhân vào hai vế với x, ta có:
  ... .0 1 2 2 3 3 4 1 1
1
n n n n n
n n n n n nx x C x C x C x C x C x C x 
       
Lấy đạo hàm hai vế ta có:
     ...
10 1 2 2 3 3 1 1
2 3 4 1 1 1
n nn n n n
n n n n n nC C x C x C x nC x n C x n x x x
 
              .
1
1 1
n
x nx x

   
Thay 1x  , ta có  . . . ... . ( ). . .0 1 2 3 1 1
2 3 4 1 2 2n n n
n n n n n nC C C C n C n C n 
        
Hết

Toan pt.de019.2010(+17de)

More Related Content

What's hot

Similar to Toan pt.de019.2010(+17de)

More from BẢO Hí

Recently uploaded

Toan pt.de019.2010(+17de)