Đề thi thử đại học lần 1 môn Toán năm học 2011-2012 gồm nhiều bài tập từ khảo sát hàm số, giải phương trình, đến tính thể tích khối chóp và các bất đẳng thức. Đề bài yêu cầu học sinh giải các bài toán phức tạp liên quan đến đại số, hình học không gian và khai triển nhị thức. Nội dung thi thử phản ánh kiến thức cần thiết cho kỳ thi đại học với các dạng bài tập phong phú.

1. 1
SỞ GIÁO DỤC & ĐÀO TẠO BẮC NINH ĐỀ THI THỬ ĐẠI HỌC LẦN 1 NĂM HỌC 2011 – 2012
TRƯỜNG THPT NGUYỄN ĐĂNG ĐẠO MÔN: TOÁN KHỐI A
Thời gian làm bài: 180 phút
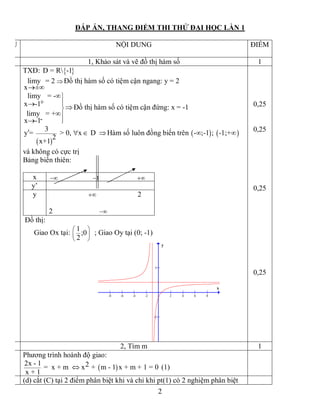
CÂU I ( 2 điểm): Cho hàm số:
2 1
1
x
y
x
-
=
+
(C)
1, Khảo sát sự biến thiên và vẽ đồ thị (C) của hàm số.
2, Gọi I là giao điểm của 2 đường tiệm cận của (C). Tìm m để đường thẳng (d): y x m= + cắt (C) tại 2 điểm
phân biệt A và B sao cho diện tích tam giác IAB bằng 4.
CÂU II ( 2 điểm):
1, Giải phương trình: ( )( ) 2 cos 1
2 1 sin 1 tan
sin cos
x
x x
x x
-
+ + =
+
2, Giải hệ phương trình: { 4
2 2
5 6
5 6
x y
x y x
+ =
+ =
, ( ) , x y RÎ
CÂU III ( 1 điểm): Tìm m để phương trình sau có 2 nghiệm thực phân biệt thuộc [ ] 0;2 :
4 4 2 1 0 x x
m+ - - =
CÂU IV ( 2 điểm): Cho hình chóp S.ABCD có đáy ABCD là hình bình hành có góc 0
60 BACÐ = ; AB = a;
AC = 4a. Hai mặt phẳng (SAB) và (SAC) cùng vuông góc với đáy; SD tạo với đáy góc 0
45 .
1, Tính thể tích khối chóp.
2, Gọi E, F lần lượt là trung điểm của BC và SD. Tính khoảng cách giữa hai đường thẳng DE và CF.
CÂU V ( 1 điểm): Cho a, b, c là 3 số thực dương thoả mãn: 1 abc ³ . Chứng minh rằng:
1 1 1 27
1 1 1 8
a b c
a b c
æ öæ öæ ö
+ + + ³ç ÷ç ÷ç ÷
+ + +è øè øè ø
CÂU VI ( 1 điểm):
Trong mặt phẳng toạ độ Oxy cho 3 đường thẳng 1 : 2 6 0 d x y+ - = ; 2 : 2 0 d x y+ = và 3 :3 2 0 d x y- - = .
Viết phương trình đường tròn (C) có tâm I thuộc d3, cắt d1 tại A và B, cắt d2 tại C và D sao cho tứ giác
ABCD là hình vuông.
CÂU VII ( 1 điểm):
Cho khai triển: ( )
2 2 2
0 1 2 2 3 1 ... ...
n k n
n k x a a x a x a x a x+ = + + + + + + , ( ) , ;0 2 k n N k nÎ £ £
Biết rằng: ( ) 0 1 2 2 ... 1 ... 4096
k
n k a a a a a- + - + - + + = . Tìm hệ số của 8
x trong khai triển.
………………….Hết………………..
( Cán bộ coi thi không giải thích gì thê
Thi thử Đại học www.toanpt.net

2. 2
ĐÁP ÁN, THANG ĐIỂM THI THỬ ĐẠI HỌC LẦN 1
U NỘI DUNG ĐIỂM
1, Khảo sát và vẽ đồ thị hàm số 1
TXĐ: { } D = R ­1
limy = 2
x ±® ¥
Þ Đồ thị hàm số có tiệm cận ngang: y = 2
limy = ­
+ x ­1
limy = +
­ x ­1
ü
ïï
ý
ï
ïþ
¥
® Þ
¥
®
Đồ thị hàm số có tiệm cận đứng: x = ­1
( )
3
y = > 0, x D
2
x+1
¢ " Î ÞHàm số luôn đồng biến trên ( ) ( ) ­ ;­1 ; ­1;+¥ ¥
và không có cực trị
Bảng biến thiên:
x -¥ 1- +¥
y’
y +¥ 2
2 -¥
Đồ thị:
Giao Ox tại:
1
;0
2
æ ö
ç ÷
è ø
; Giao Oy tại (0; ­1)
­8 ­6 ­4 ­2 2 4 6 8
­5
5
x
y
0,25
0,25
0,25
0,25
2, Tìm m 1
Phương trình hoành độ giao:
( )
2x ­ 1 2 = x + m x + m ­ 1 x + m + 1 = 0
x + 1
Û (1)
(d) cắt (C) tại 2 điểm phân biệt khi và chỉ khi pt(1) có 2 nghiệm phân biệt

3. 3
m > 3 + 2 3 2 Δ = m ­ 6m ­ 3 > 0
m < 3 ­ 2 3
é
ê
êë
Û Û (A)
Gọi ( ) ( ) ( ) A x ; x + m ; B x ; x + m , x x
1 1 2 2 1 2
¹
( ) ( )
2 2
AB = 2 x ­ x = 2 x + x ­ 4x x
2 1 1 2 1 2
é ù
Þ ê ú
ë û
Theo Viet:
x + x = 1 ­ m
1 2
x x = m + 1
1 2
ì
ï
í
ïî
( ) 2 AB = 2 m ­ 6m ­ 3Þ
I là giao điểm của 2 tiệm cận ( ) I ­1;2Þ
m ­ 3
d = d =
I,AB I,d 2
æ ö æ ö
ç ÷ ç ÷
è ø è ø
2 m ­ 3 m ­ 6m ­ 3 1
S = AB.d =
IAB I,AB 2 2æ ö
ç ÷
è ø
Þ
D
( ) ( ) 2 2 S = 4 m ­ 3 m ­ 6m ­ 3 = 64
ΔIAB
Û
( ) ( )
( ) ( )
( )
( )
2 2
m ­ 3 m ­ 3 ­ 12 = 64
4 2
m ­ 3 ­ 12 m ­ 3 ­ 64 = 0
2
m ­ 3 = ­4 m = 7 (t/m)
2 m = ­1 (t/m)
m ­ 3 = 16
é ù
ê ú
ë û
é
éê
êê
êëê
ë
Û
Û
Û Û
Vậy: m = 7; m = ­1 là các giá trị phải tìm.
0,25
0,25
0,25
0,25
1, Giải phương trình lượng giác 1
Đk:
cosx 0
sinx + cosx 0
ìï
í
ïî
¹
¹
Khi đó, pt tương đương: ( )
1 cosx­1
2 1+sinx =
2 sinx+cosx cos x
2 cosx ­ 1
=
1 ­ sinx sinx + cosx
sinx + cosx + sinxcosx + 1 = 0
Û
Û
( )( ) sinx+1 cosx+1 = 0Û
sinx = ­1
cosx = ­1
é
Û ê
ë
x = π + k2πÛ
0,25
0,25
0,25
( loại )
( t/m )

4. 4
0,25
2, Giải hệ phương trình 1
Trừ từng vế của 2 phương trình ta được:
( ) ( ) 2 3
2
x = y
x ­ y x x + y ­ 5 = 0 5­x
y =
x
é
êé ù Ûë û ê
êë
*) Với: x = y, thay vào pt(1) ta có: x 4
+ 5x – 6 = 0
( )( )( ) 2
x ­ 1 x + 2 x ­ x + 3 = 0
x = 1 y = 1
x = ­2 y = ­2
Û
Þé
Û ê Þë
*) Với:
3
2
5 ­ x
y=
x
, thay vào pt(1) ta có:
3
4 4
2 2 2
25 ­ 5x 25 25
x + = 6 x + + ­ 5x = 6 (*)
x 2x 2x
Û
Từ (2)
2 2
6­5x y 6
x = ­5x ­6
5 5
Þ £ Þ ³ (a)
Lại có: 3 25 25 625 4x + + 3 > 12
2 2 4 2x 2x
³ (b)
Cộng từng vế của 2 bất đẳng thức (a) và (b) suy ra: VT(*) > 6 Þ(*) vô
nghiệm
Vậy hệ đã cho có 2 nghiệm (x ; y) = (1 ; 1); (­2; ­2).
0,25
0,25
0,25
0,25
Tìm m để pt có 2 nghiệm phân biệt [ ] 0 ; 2Î 1
Đặt: [ ] x
2 =t, t 1 ; 4Î
Pt trở thành: 2
t +4=m t­1
t = 1 không là nghiệm của pt. Do đó pt tương đương:
2
t + 4
= m (1)
t ­ 1
Pt đã cho có 2 nghiệm phân biệt [ ] 0 ; 2Î khi và chỉ khi pt(1) có 2 nghiệm
phân biệt ( ] 1 ; 4Î
Xét: ( )
2
t + 4
f t =
t ­ 1
trên (1 ; 4]
2
3t ­ 4t ­ 4
f (t) =
(t ­ 1) t ­ 1
¢
t = 2
f (t) = 0 2
t = ­
3
é
ê¢ Û
ê
ë
Bảng biến thiên:
0,25
0,25

5. 5
t 1 2 4
f’(t) ­ 0 +
f(t)
+¥
20
3
8
Từ bảng biến thiên suy ra:
20
8 < m
3
£ là các giá trị cần tìm
0,25
0,25
Hình học không gian
1, Tính thể tích khối chóp 1
Ta có:
(SAB) (ABCD)
SA (ABCD)
(SAC) (ABCD
^ ü
Þ ^ý
^ þ
SDAÞ Ð là góc giữa SD và (ABCD)
0
SDA = 45Þ Ð
Trong ΔABC có:
( ) 2 2 2
BC = AB + AC ­ 2AB.ACcos BACÐ
2
= 13a AD = BC = a 13Þ
Trong tam giác SAD vuông tại A, ta có:
SA = ADtan( SDA) = a 13Ð
2
ABCD ΔABC S = 2S = AB.ACsin(BAC) = 2a 3
3
S.ABCD ABCD
1 2a 39
V = SA.S =
3 3
Þ
2, Tính khoảng cách giữa DE, CF
0,25
0,25
0,25
0,25
1
Trong mp(ABCD), dựng CI // ED ( I AD )Î ED // (CFI)Þ
(DE,CF) (DE,(CFI)) (D,(CFI)) d = d = dÞ
Gọi H là trung điểm của AD ÞD là trung điểm HI Þ (D,(CFI)) (H,(CFI))
1
d = d
2
Hạ HK vuông góc với CI tại K; HJ vuông góc với FK tại J
Ta có:
FH // SA FH (ABCD) FH CI CI (FHK) (FCI) (FHK)Þ ^ Þ ^ Þ ^ Þ ^
(H,(FCI)) HJ (FCI) HJ = dÞ ^ Þ
Ta thấy: 2
ΔHCI ABCD
1
S = S = a 3
2
ΔHCI 2S
HK =
CI
Þ
Ta có:
2 2 2
AD +CD ­AC 1 1
cos( ADC) = = ­ cos( BCD)=
2AD.CD 13 13
Ð Þ Ð
2 2 a 13
CI = DE = DE +CD ­2DE.CD.cos(BCD) =
2
0,25
0,25
S
A
B C
D
E
F
J IH
K

6. 6
4a 3
HK =
13
Þ
1 a 13
HF = SA =
2 2
Trong tam giác FHK vuông tại H, có:
2 2 2 2 2 2
1 1 1 13 4 361
= + = + =
HJ HK HF 48a 13a 624a
( ) D,(CFI)
4a 39 2a 39
HJ = d =
19 19
Þ Þ
Vậy: (DE, CF)
2a 39
d =
19
0,25
0,25
Bất đẳng thức 1
Ta có: ( ) ( ) ( )
a+1 1 3 3 1 3
+ + a+1 1+ a+1 a+ a+1 0
4 a+1 4 4 a+1 4
³ Þ ³ >
Tương tự: ( )
1 3
b+ b+1 0
b+1 4
³ >
( )
1 3
c+ c+1 >0
c+1 4
³
( )( )( )
27 27 27
VT a+1 b+1 c+1 abc
64 8 8
Þ ³ ³ ³ (đpcm)
0,5
0,25
0,25
Phương pháp toạ độ trong mặt phẳng 1
Gọi I(a; 3a – 2)
Vì ABCD là hình vuông Þd(I, AB) = d(I, CD) = d
7a ­ 10 7a ­ 4 3
= a = 1 I(1;1) d =
5 5 5
Û Û Þ Þ
Bán kính:
3 2
R = d 2 =
5
Þpt(C): ( ) ( )
2 2 18
x ­ 1 + y ­ 1 =
5
0,25
0,25
0,25
0,25
Nhị thức Niu­Tơn 1
Ta có: ( )
2n 2 k 2n
0 1 2 k 2n 3x + 1 = a + a x + a x +...+ a x +...+ a x
Thay x = ­1, ta có: (­2) 2n
= a0 – a1 + a2 ­ … + (­1) k
ak +…+ a2n
Từ giả thiết suy ra: (­2) 2n
= 4096 n = 6Þ
Với n = 6, ta có khai triển:
( )
12 0 1 2 2 12 12
12 12 12 12 1+3x =C + C .(3x) + C (3x) +...+ C (3x)
ÞHệ số của x 8
trong khai triển là: 8 8
12 C .3
0,25
0,25
0,25
0,25
A B
CD
I
d

7. 7