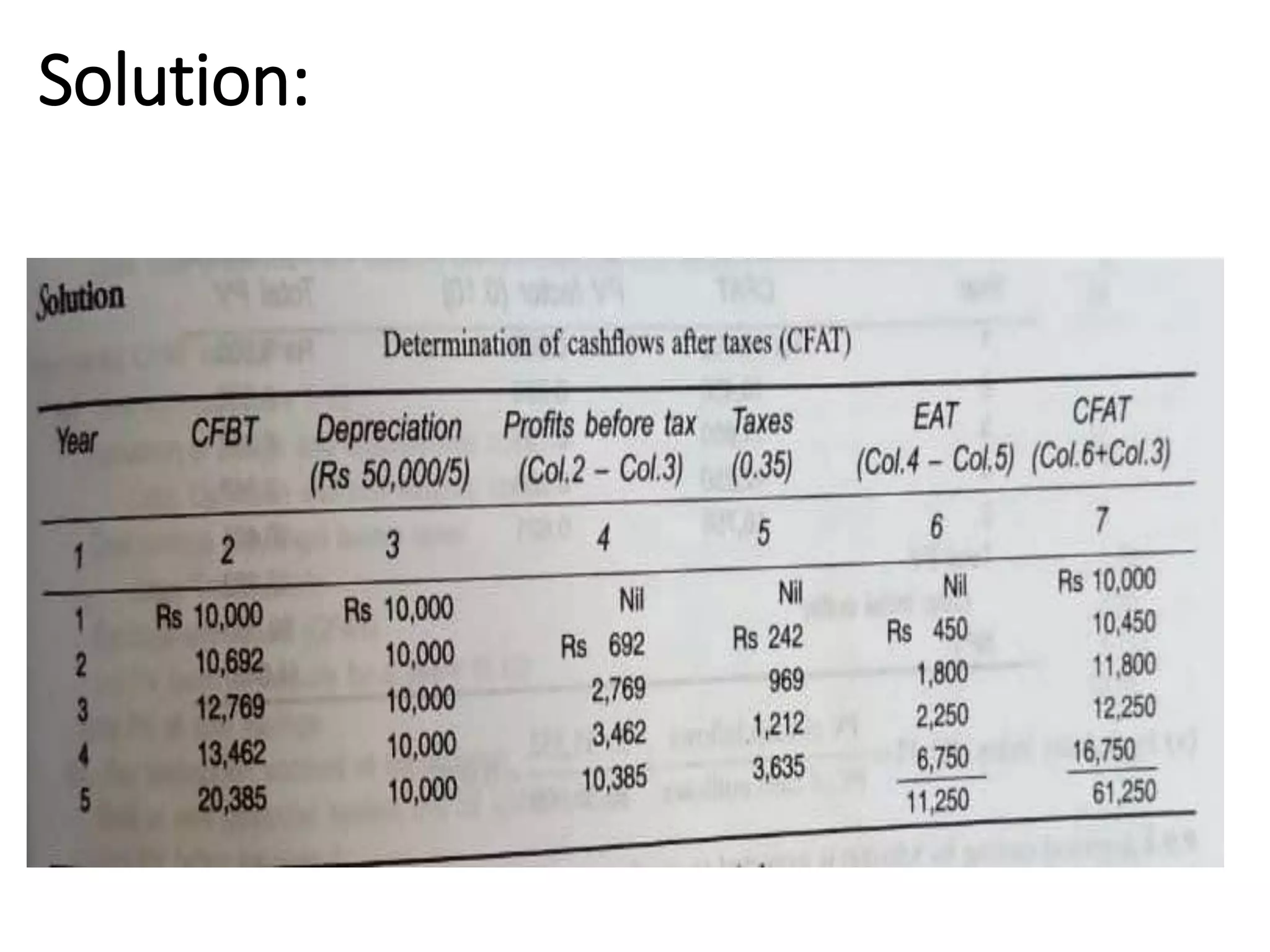
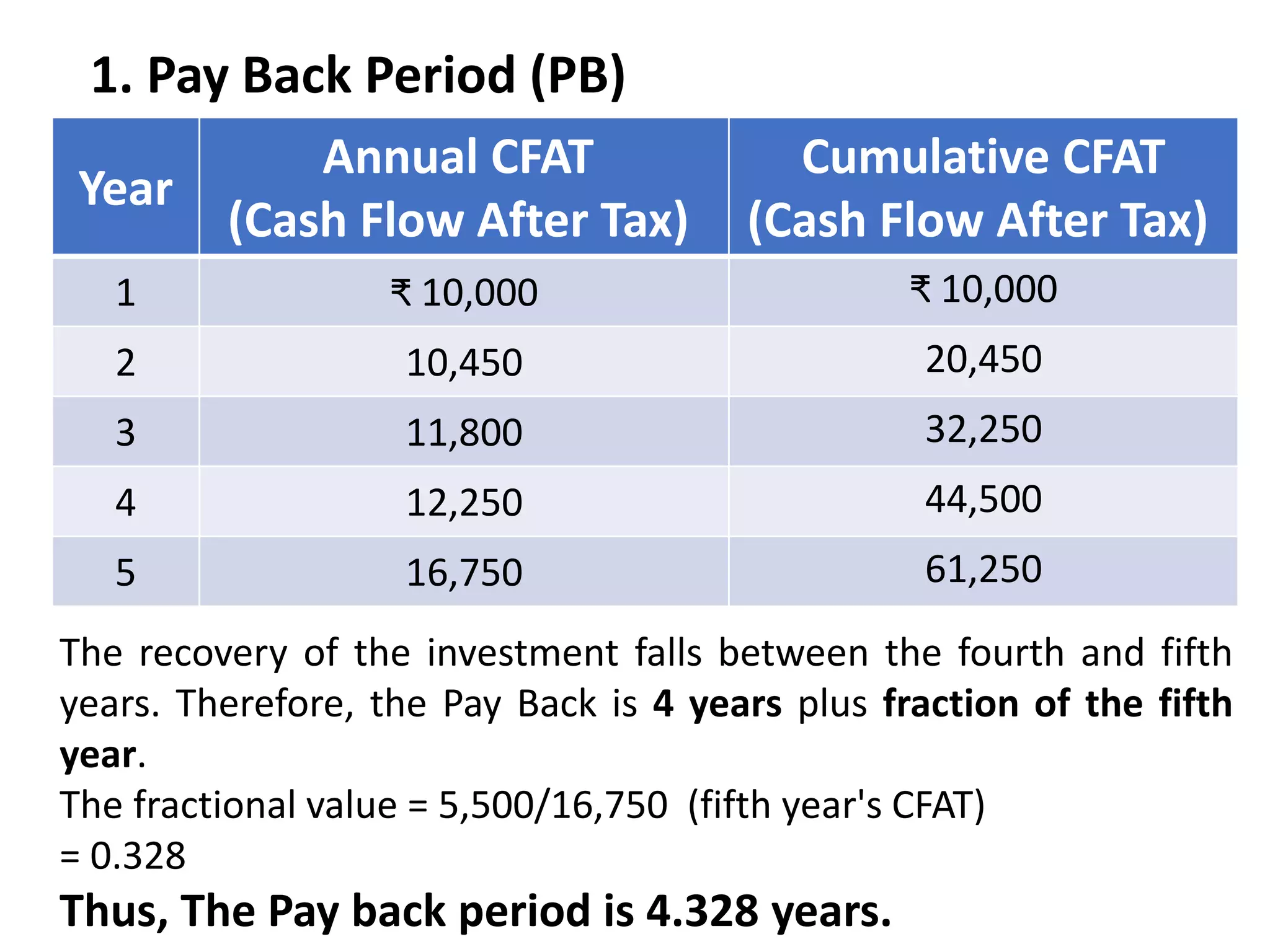
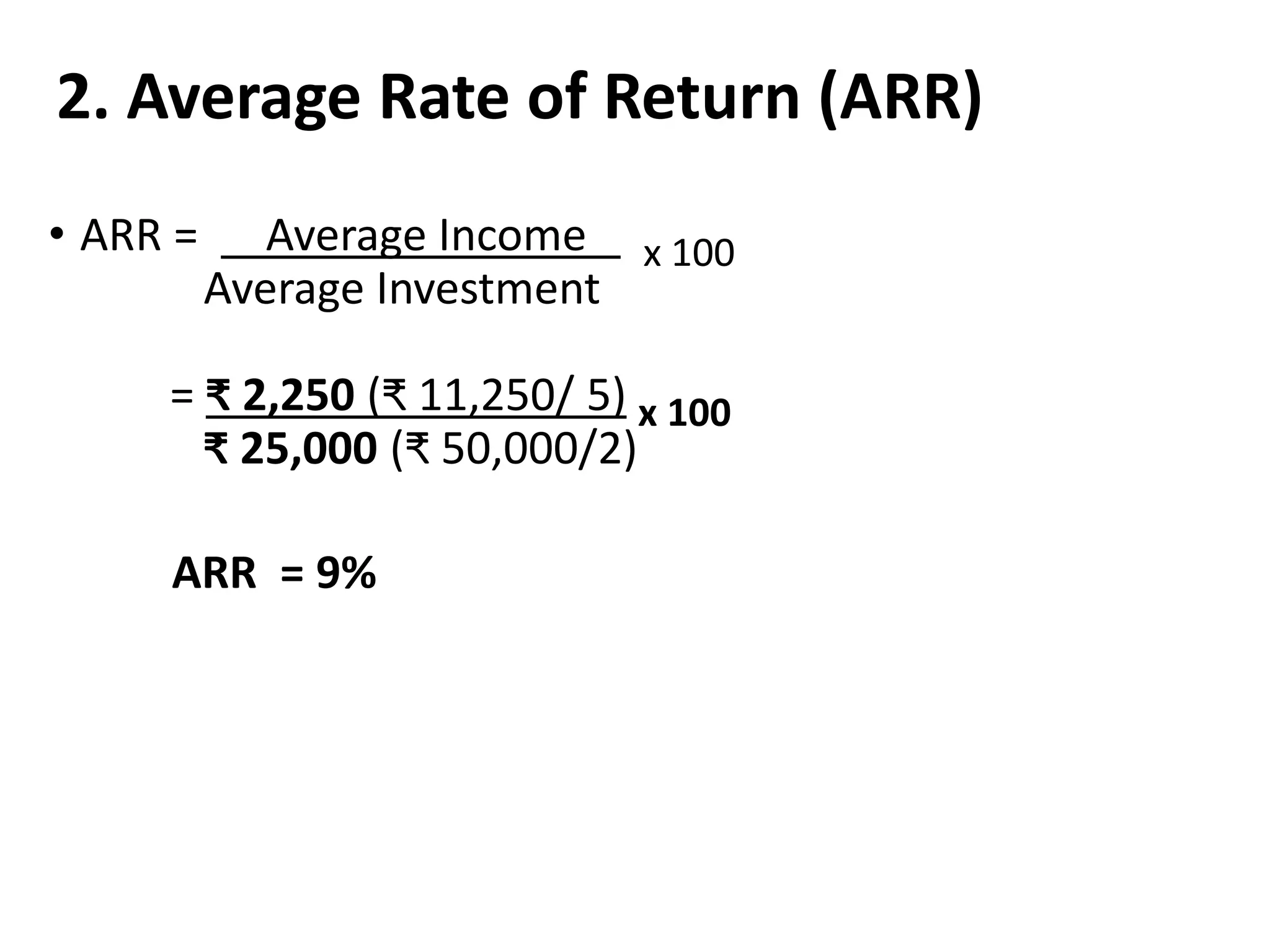
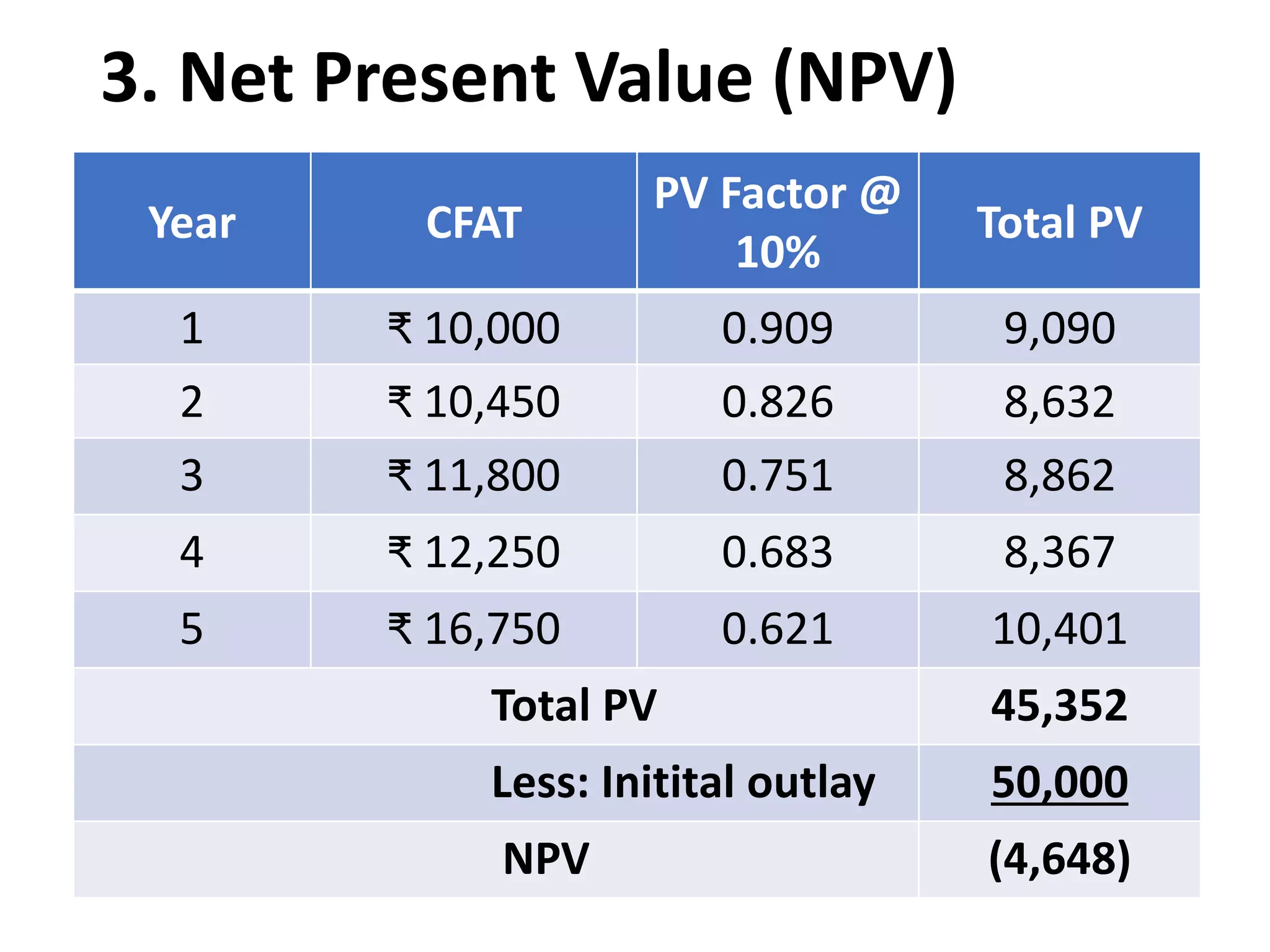
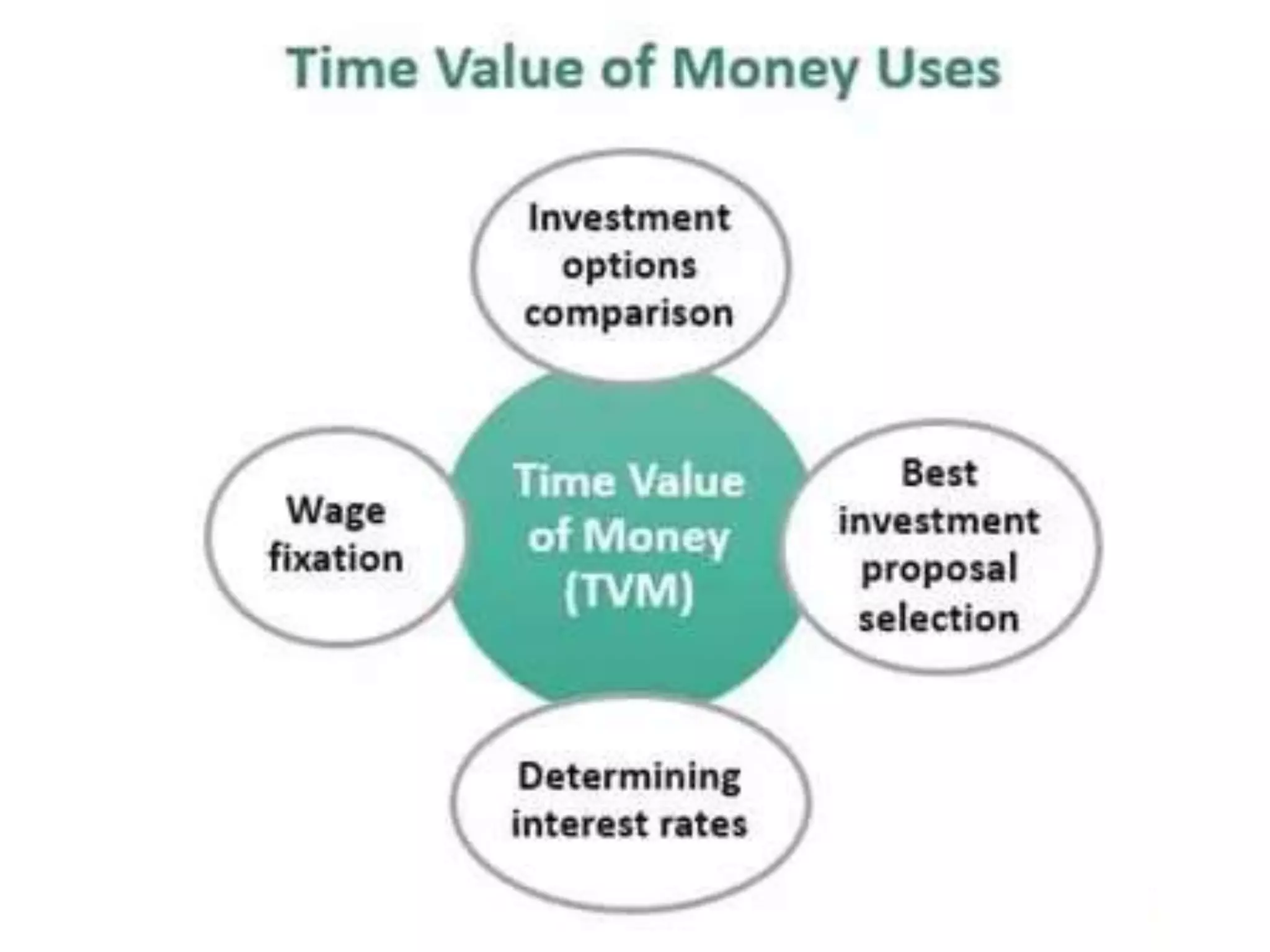
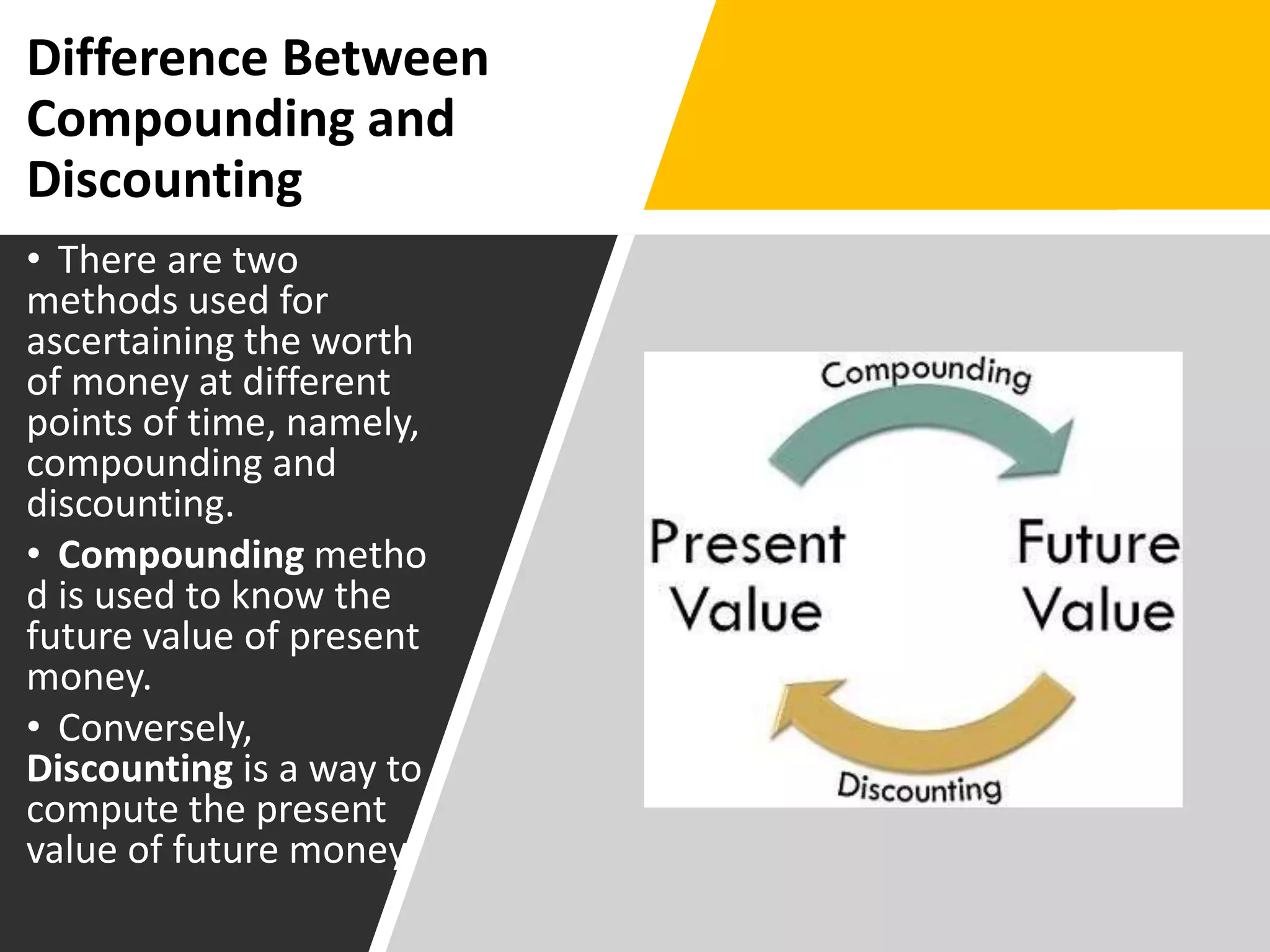
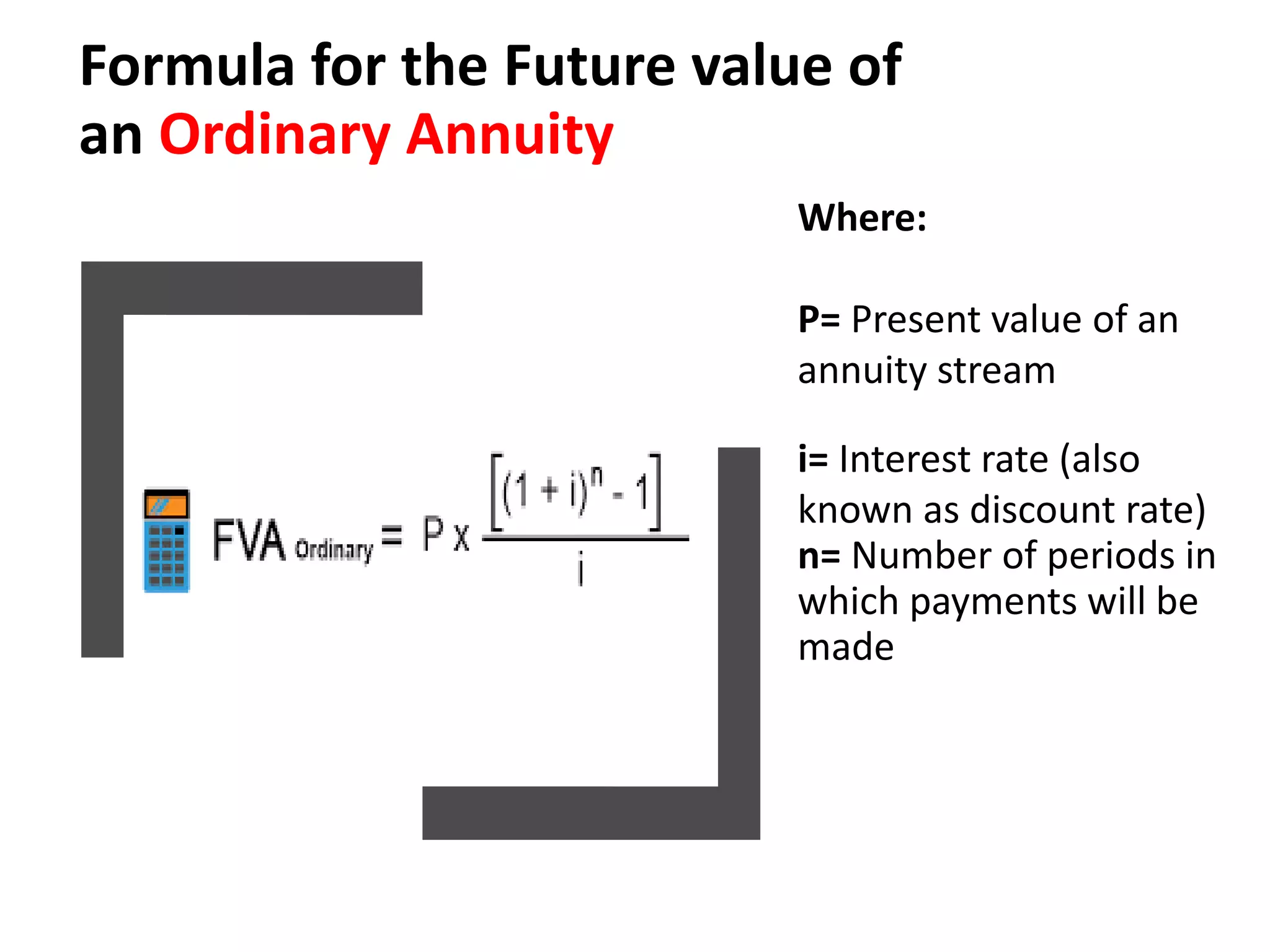
The document discusses various concepts related to time value of money and capital budgeting. It defines time value of money as the principle that money available now is worth more than the same amount in the future. It then discusses practical applications of time value techniques in investment decisions. The document also covers compounding and discounting methods, formulas for calculating future and present values of single amounts and annuities. Finally, it discusses various capital budgeting techniques like payback period, accounting rate of return, net present value, internal rate of return, and profitability index.

1. Time Value of Money
& Capital Budgeting
UNIT- V

2. Time value
of Money

3. Introduction
• Time Value of Money (TVM) is a
fundamental financial concept
stating that money available at
the present time is worth more
than the same amount in the
future due to its potential earning
capacity.
• This core principle of finance
holds that, provided money can
earn interest, any amount of
money is worth more the sooner
it is received.

5. Practical Application of Time Value Technique
The financial firms use TVM for the following purposes:
• It helps in comparing the investment alternatives
available in the market. Investors choose the best
investment proposals based on the evaluation,
considering the TVM.
• TVM helps investors make the best investment
decisions, knowing the future returns they should
expect from what they invest.
• Lenders decide the interest rates for loans, mortgages,
etc., based on the present and future value of an
amount.

6. • Money loses its value over time, which causes
inflation affecting the buying power of the public.
• The value of money, when known, helps in fixing
appropriate Salary, wages and prices of products.

7. Difference Between
Compounding and
Discounting
• There are two
methods used for
ascertaining the worth
of money at different
points of time, namely,
compounding and
discounting.
• Compounding metho
d is used to know the
future value of present
money.
• Conversely,
Discounting is a way to
compute the present
value of future money.

8. Compounding:
• Under compounding technique, the interest
earned on the initial principal become
part of principal at the end of
compounding period. Since interest goes on
earning interest over the life of the asset,
this technique of time value of money is also
known as ‘compounding’.

9. • The process of determining the future value
of present money is called compounding. In
other words, compounding is a process of
investing money, reinvesting the
interest earned & finding value at the end of
specified period.

10. Formula of
Compounding
In general: The value of
money after nth period
can be calculated as:
FV = PV (1 + r)^n
Where,
FV= Future value of
money,
PV = Present value of
money,
r = Compound interest
rate.
n = Time Period

11. Future Value of Single Amount &
Annuity
• The value of a current single amount taken to a
future date at a specified interest rate is called
the future value of a single amount.
• In this case, “future value” means the amount to
which the investment will grow at a future date
if interest is compounded. The single amount refers
to a lump sum invested at the beginning of a period
(e.g., year 1) and left intact for all periods.

12. Formula for
Calculating
Future
value of a
Single
Amount

13. Question
• Assume you put ₹
20,000 (principal)
in a bank for the
interest rate of
4%. How much
money will the
bank give you
after 10 years
with
compounding
interest rate?

14. Answer
Given data
• FV=PV (1+r)^n
• =20,000 x (1+0.04) ^ 10
• =20,000*1.48024
• =29604.8
• So the bank will pay you 29604.8
after 10 years.

15. Question
• Mr. Gaurav deposited amount
of Rs. 10,000 compounded
annually for 3 years at 12%,
then what will be the future
value of Rs. 10,000 after 3
years.

16. Solution
Future Value = P x (1+i) n
Given data,
P = 10,000
i = 12%
n = 3 years
= 10,000 (1 + 0.12)3
= 14,049.28

17. Another
Formula for
Time Value of
Money/
Compounding
• Depending on the exact situation,
the formula for the time value of
money may change slightly. But in
general, the most fundamental TVM
formula considers the following
variables:
• FV = Future value of money
• PV = Present value of money
• i = interest rate
• n = number of compounding periods
per year
• t = number of years
Based on these variables, the formula
for TVM is:
• FV = PV x [ 1 + (i / n) ] (n x t)

18. Question
Q. Assume a sum of Rs. 10,000 is invested for one year
at 10% interest compounded annually. The future
value of that money is:

19. Answer:
Given data,
PV= 10,000
i = 10%
t = 1
n= 1
Formula for calculating Future Value is;
FV = PV x [ 1 + (i / n) ] (n x t)
FV = Rs. 10,000 x [1 + (0.10 / 1)] (1 x 1)
= Rs. 11,000
The Future value of that money is Rs. 11,000/-.

20. Effect of different Compounding Periods on
Future Value
• Q. Assume a sum of Rs. 10,000 is invested for one
year at 10% interest. if the number of compounding
periods is increased to quarterly, monthly, and daily,
then what will be the future value?

21. Answer
Quarterly Compounding:
FV = ₹ 10,000 x [1 + (10% / 4)] (4 x 1)
= Rs. 11,038
Monthly Compounding:
FV = ₹ 10,000 x [1 + (10% / 12)] (12 x 1)
= Rs. 11,047
Daily Compounding:
FV = ₹ 10,000 x [1 + (10% / 365)] (365 x 1)
= Rs. 11,052

22. Future Value of an Annuity
• The future value of an annuity is the value of a group
of recurring payments at a certain date in the future,
assuming a particular rate of return, or discount rate.
The higher the discount rate, the greater the
annuity's future value.

23. Future Value of an
Ordinary Annuity and
Annuity Due
• In ordinary
annuities,
payments are
made at the end of
each period.
• In annuities due,
they're made at
the beginning of
the period.
• The future value of
an annuity is the
total value of
payments at a
specific point in
time.

24. Formula for the Future value of
an Ordinary Annuity
Where:
P= Present value of an
annuity stream
i= Interest rate (also
known as discount rate)
n= Number of periods in
which payments will be
made

25. Question
• Mr. Vinod decides to invest
Rs. 125,000 per year for the
next five years in an annuity
they expect to compound at
8% per year. Calculate The
expected future value of this
payment stream.

26. Solution:
FV = P × ((1+i)n−1)
i
Where:
• FV = Future value of an annuity stream
• PMT = 1,25,000
• i = 8%
• n = 5 years.
Future Value = Rs. 125,000× ((1+0.08)5 −1)
0.08
= Rs. 733,325

27. Formula for the Future value of an
Annuity Due
Where:
P=Present value of an
annuity stream
PMT= Amount of each
annuity payment
r=Interest rate (also
known as discount rate)
n=Number of periods in
which payments will be
made

28. Question
• John Doe, who plans to
deposit ₹ 5,000 at the
beginning of each year for
the next seven years to
save enough money for his
daughter’s education.
Determine the amount
that John Doe will have at
the end of seven years.
Please note that the
ongoing rate of interest in
the market is 5%.

29. Solution:
Given Data,
P= ₹ 5,000
r= 5% or 0.05
n= 7 years
Future Value =
FV = 5,000 [(1 + 0.05)7 – 1] x (1+ 0.05)
0.05
= ₹ 42,745.54

30. Discounting
• The concept of compounding and
discounting are similar. Discounting brings a
future sum of money to the present time
using discount rate and compounding brings
a present sum of money to future time.
• In economic evaluations, “discounted” is
equivalent to “present value” or “present
worth” of money.

31. Present
Value of a
Single
Amount
• The value of a future promise to pay
or receive a single amount at a
specified interest rate is called the
present value of a single amount.
• Many times in business and life, we
want to determine the value today
of receiving a specific single amount
at some time in the future.
• For example, suppose you want to
know the value today of receiving
$15,000 at the end of 5 years if a
rate of return of 12% is earned.

32. • Present value states that an amount of money
today is worth more than the same amount in the
future.
• In other words, present value shows that money
received in the future is not worth as much as an
equal amount received today.
• It shows you how much a money that you are
supposed to have in the future is worth to you
today.

33. Formula For Present Value of a Single Amount
• In this formula, the
following variables are
defined as:
• PV = Present value of
the amount
• FV = Future value of
the amount (amount to
be received in future)
• i = Interest rate (in
percentage terms)
• n = Number of periods
after which the amount
will be received in
future

34. Question
• Suppose a company expects to
receive $8,000 after 5 years.
Calculate the present value of
this sum if the current market
interest rate is 12% and
the interest is compounded
annually.

35. Solution
In this example, the number of periods (n) is 5 and the interest
rate (i) is 12%. Therefore, the present value (PV) is calculated as
follows:
PV = FV x 1 / (1+i)n
= 8,000 x 1 / (1+12%)5
= 8,000 x 1 / (1+0.12)5
= 8,000 x 1 / (1.12)5
= 8,000 x 1 / 1.7623
= 8,000 x 0.5674
= $4,540
According to these results, the amount of $8,000, which will be
received after 5 years, has a present value of $4,540.

36. Question
• Assuming the discount rate of
10%, Calculate the present
value of ₹100 which will be
received in 5 years from now.

37. Solution
Given data
• F= ₹100
• n =5
• i =0.1
P = F[1/(1 + i)n]
= 100[1/(1 + 0.1)5]
= ₹ 62.09

38. Present Value of an Annuity
• The present value of an annuity is the current value
of all the income that will be generated by that
investment in the future. In more practical terms, it
is the amount of money that would need to be
invested today to generate a specific income.

39. • An ordinary annuity makes payments at the
end of each time period, while an annuity
due makes them at the beginning.
• The formula for the present value of
an ordinary annuity, as opposed to
an annuity due.

40. Formula for the present value of
an ordinary annuity
Where:
P=Present value of an an
nuity stream
PMT= Amount of each a
nnuity payment
r=Interest rate (also kno
wn as discount rate)
n=Number of periods in
which payments will be
made​

41. Question
• Assume a person has the
opportunity to receive an
ordinary annuity that pays
$50,000 per year for the
next 25 years, with a 6%
discount rate, or take a
$650,000 lump-sum
payment.
• Which is the better option?

42. Solution:
Given this information, the annuity is worth $10,832 less
on a time-adjusted basis, so the person would come out
ahead by choosing the lump-sum payment over the
annuity.

43. Formula The formula for the present value of
an Annuity due, (in which payments are made at the
beginning of each period)
With an annuity due,
in which payments
are made at the
beginning of each
period, the formula is
slightly different. To
find the value of an
annuity due, simply
multiply the above
formula by a factor of
(1 + r):

44. Question
• Assume a person has
the opportunity to receive
an ordinary annuity that
pays $50,000 per year for
the next 25 years, with a 6%
discount rate, or take a
$650,000 lump-
sum payment.
• if the example above
referred to an annuity due,
rather than an ordinary
annuity, What will be the
present value?

45. Solution
• In this case, the person should choose the annuity due
option because it is worth $27,518 more than the
$650,000 lump sum.

47. Introduction
• Capital Budgeting is used for decision making of
the long-term investment that whether the
projects are fruitful for the business and will
provide the required returns in the future years.
• Capital budgeting is the process of evaluating and
selecting long-term investments that
are consistent with the goal of shareholders
(owners) wealth maximization.

48. Nature of
Capital
Budgeting:
• Capital budgeting is the process
of making investment decisions
in capital expenditures.
• A capital expenditure may be
defined as an expenditure the
benefits of which are expected
to be received over long period
of time exceeding one year.

49. • It is a long-term investment decision.
• It is irreversible in nature.
• It requires a large amount of funds.
• It is most critical and complicated decision
for a finance manager.
• It involves an element of risk as the
investment is to be recovered in future.

50. Need, Significance or Importance of
Capital Budgeting
• Large Investments: Capital budgeting decisions,
generally, involve large investment of funds. But the
funds available with the firm are always limited.
Hence, it is very important for a firm to plan and
control its capital expenditure.
• Long term Effect on Profitability: Capital
expenditures have great impact on business
profitability in the long run. If the expenditures are
incurred after preparing proper capital budget,
then there is a possibility of increasing profitability
of the firm.

51. • Irreversible decisions in Capital Budgeting: Whenever
a project is selected and made investments in the form
of fixed assets, such investments is irreversible in
nature. If the management wants to dispose of these
assets, there is a heavy monetary loss.
• Risk and uncertainty in Capital budgeting: The future is
uncertain and full of risks. Capital budgeting decision is
surrounded by great number of uncertainties. Longer
the period of project, greater may be the risk and
uncertainty. The estimates about cost, revenues and
profits may not come true.

52. • Difficult to make decision in Capital budgeting: Capital
budgeting is a difficult and complicated exercise for the
management. These decisions require an over all
assessment of future events which are
uncertain. uncertainties caused by economic-political
social and technological factors.
• Permanent Commitments of Funds: The investment
made in the project results in the permanent
commitment of funds. The greater risk is also involved
because of permanent commitment of funds.

53. • National Importance: The selection of any project
results in the employment opportunity, economic
growth and increase per capita income.

54. Techniques of
Capital Budgeting
A] Traditional Methods
1. Pay Back Method.
2. Accounting rate of return.
B] Discounted Cash Flow Methods (DCF)
1. Net Present Value Method (NPV)
2. Internal Rate of Return (IRR)
3. Profitability index.

55. Pay Back Method
• This method refers to the period in which
the proposal will generate cash to recover
the initial investment made. It purely
emphasizes on the cash inflows, economic
life of the project and the investment made
in the project, with no consideration to
time value of money.

56. Methods of
Calculating
payback
period.
There are two ways of calculating
payback period.
1. Annuity: Annuity is a stream of equal
cash inflows. In such a situation, the
initial cost of the investment is divided
by the constant annual Cash flow
• Payback period = Investment
Constant annual cash flow
E.g. An Investment of Rs. 40,000 in a
machine is expected to produce Cash
Flow After Tax (CFAT) of Rs. 8,000 for 10
years. Calculate the payback period.
PB= Rs. 40,000/ Rs. 8000
PB = 5 years

57. 2. Mixed Stream: This method is used when a
projects cash flows are not uniform. Mixed
stream of cash inflows exhibiting any pattern
other than that of an annuity.

58. Question: The initial investment of Machine A & B is
Rs. 56,125. Expected cash inflow from the machines are
given below. Advice the Company which machine they
should prefer by using pay back period method.
Year
Annual CFAT (Cash Flow After Tax)
A B
1 Rs. 14,000 Rs. 22,000
2 16,000 20,000
3 18,000 18,000
4 20,000 16,000
5 25,000 17,000

59. Solution
Year
Annual CFAT (Cash
Flow After Tax)
Cumulative CFAT
(Cash Flow After Tax)
A B A B
1 Rs. 14,000 Rs. 22,000 Rs. 14,000 Rs. 22,000
2 16,000 20,000 30,000 42,000
3 18,000 18,000 48,000 60,000
4 20,000 16,000 68,000 76,000
5 25,000 17,000 93,000 93,000

60. Solution:
• The initial investment of Machine A & B is Rs. 56,125
• Machine 'A': Machine A will be recovered initial
investment between year 3 and 4.
• The sum of Rs. 48,000 is recovered by the end of 3
years. The balance Rs. 8,125 is needed to be
recovered in the fourth year. In the fourth year CFAT is
Rs. 20,000. The pay back fraction is therefore 0.406
(Rs.8,125/Rs. 20,000).
• Therefore, Payback period of project 'A' is 3.406.

61. • Machine 'B': The recovery of the investment falls
between the second and third years. Therefore,
the Payback period of project 'B' is 2 years and
fraction of third year as Rs. 42,000 is recovered by
the end of Second Year, the balance of Rs.
14,125 needs to be recovered in the third year. In
the third year CFAT is Rs. 18,000. The pay back
fraction is 0.785 (Rs. 14,125/Rs. 18,000). Thus, the
PB period for machine 'B' is 2.785.
• As the payback period of Machine 'B' is less i.e.
2.785 as compared to Machine 'A' i.e. 3.406 hence
it is advised to purchase Machine 'B'.

62. Accounting Rate of Return /
Average Rate of Return (ARR)
• Accounting rate of return (ARR) also known as the
Return On Investment (ROI), uses accounting
information, as revealed by financial statements, to
measure the profitability of an investment.
• Acceptance Rule: Accept all those projects whose
ARR is higher than the minimum rate established by
the management and reject those projects which
have ARR less than the minimum rate.
ARR = Average Income
Average Investment

63. Net Present Value Method
• Cash flows of the investment project are
forecasted based on realistic assumptions.
• Appropriate discount rate are identified to
discount the forecasted cash flows.
• Present value of cash flows is calculated
using the opportunity cost of capital as the
discount rate.

64. • Net present value should be found out by
subtracting present value of cash outflows
from present value of cash inflows.
• NPV = PV inflows – PV outflows
• The project should be accepted if NPV is
positive (i.e., NPV > 0).

65. Acceptance
Rule
• Accept the project when NPV
is positive NPV > 0
• Reject the project when NPV
is negative NPV < 0
• May accept the project when
NPV is zero NPV = 0

66. Internal Rate of Return (IRR)
• The internal rate of return (IRR) is a discounting cash
flow technique which gives a rate of return earned by
a project. The internal rate of return is the rate of
return at which the sum of discounted cash inflows
equal the sum of discounted cash outflows.
• In other words, it is the discounting rate at which
the net present value (NPV) is zero.
Procedure of computing IRR:
I. When cash inflow are uniform for all the years.
II. When cash inflow are not uniform (Trial and
Error method)

68. I. When Cash Inflow Are Uniform For
All The Years.
Problem:
Initial investment - 1,50,000.
Life of the Asset – 6 years
Estimate cash flow ₹ 30,000.
You are required to calculate IRR

69. Solution
Computation of IRR
Present Value Factor = Initial Investment
Cash Inflow Per Year
= 1,50,000
30,000
Present Value Factor = 5
The IRR is 6%
(Note Only Understanding: Based on the two information i.e.
PV Factor = 5 & Life of asset = 6 years. Check the Annuity
table year 6 row and search the nearest value or accurate
value of the PV factor)

71. II. When cash inflow are not uniform
(Trial and Error method)
Problem:
Initial investment - 1,06,000.
Life of the Asset – 6 years
Estimate cash flow are as follows
Year 1 - ₹ 10,000
Year 2 - ₹ 15,000
Year 3 - ₹ 20,000
Year 4 - ₹ 22,000
Year 5 - ₹ 25,000
Year 6 - ₹ 28,000
You are required to calculate IRR

72. Solution
Computation of IRR
Present Value Factor = Initial
Investment
Average Cash Inflow per year
= 1,06,000 = 5.3
20,000
(Note for Understanding: Based on the two
information i.e. PV Factor = 5.3 & Life of asset = 6 years.
Check the Annuity table year 6 Row and search the nearest
value or accurate value of the PV factor there're two IRR
which are near to PV Factor 5.3 I.e. 4 % & 3%)

74. Statement Showing NPV
Year CFAT
PV Factor @ 4 %
Present
Value
1 10,000 0.962 9,620
2 15,000 0.925 13,875
3 20,000 0.889 17,780
4 22,000 0.855 18,810
5 25,000 0.822 20,550
6 28,000 0.790 22,120
Total PV of Cash Inflow 1,02,755
Less: PV of Cash outflow 1,06,000
NPV -3,245
Here the NPV is (-) which means we need to check it with Lower Percentage
I.e. 3% , If it positive then we need to go with higher %.

75. Statement Showing NPV
Year CFAT PV Factor @
4 %
Present
Value PV Factor @ 3 %
Present
Value
1 10,000 0.962 9,620 .971 9,710
2 15,000 0.925 13,875 .943 14,145
3 20,000 0.889 17,780 .915 18,300
4 22,000 0.855 18,810 .888 19,536
5 25,000 0.822 20,550 .863 21,575
6 28,000 0.790 22,120 .837 23,436
Total PV of Cash Inflow 1,02,755 1,06,702
Less: PV of Cash outflow 1,06,000 1,06,000
NPV -3,245 702
Here the One NPV is (-) one NPV is positive then we need to stop the process
and find out the exact NPV with the help of NPV

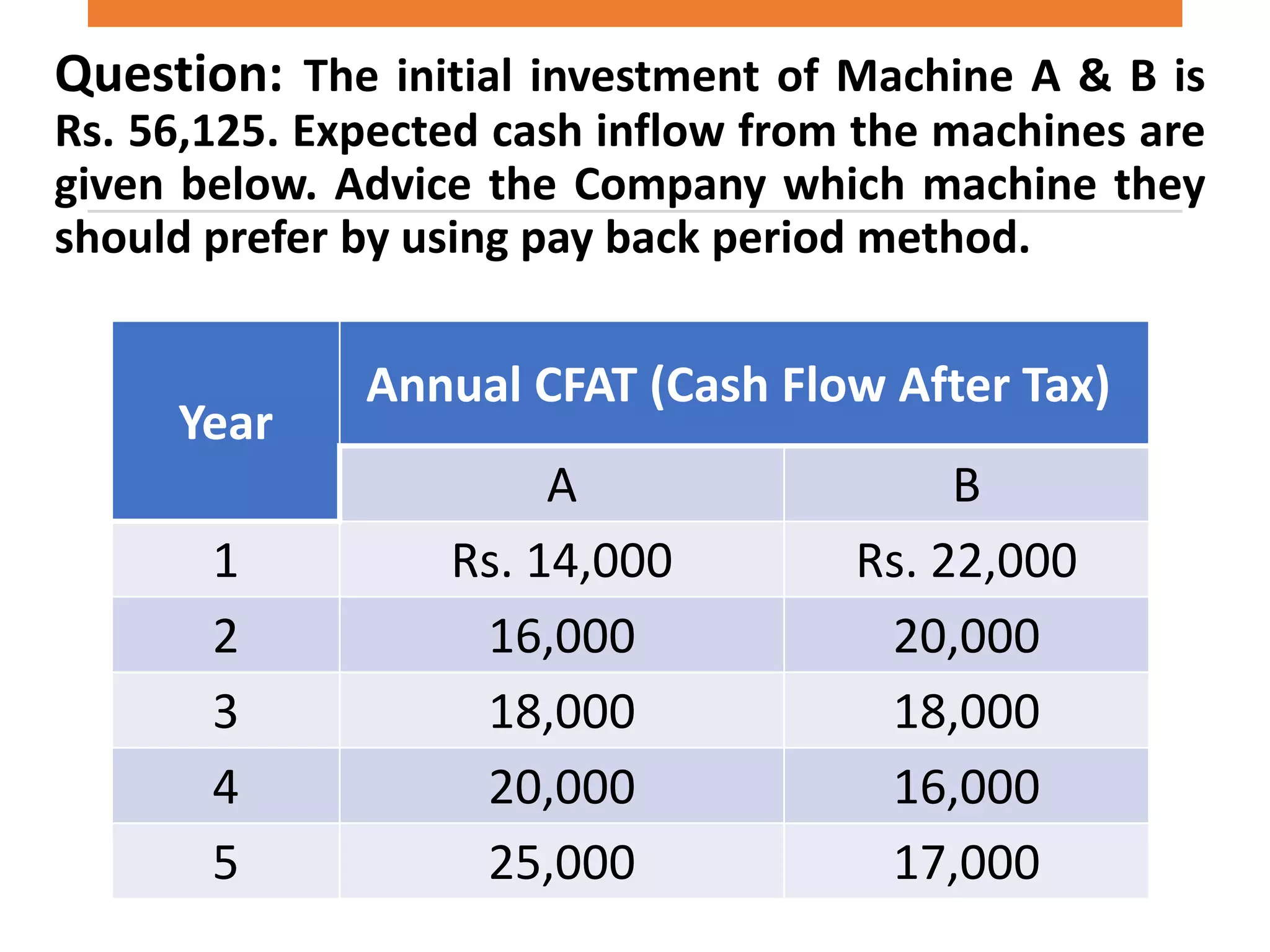
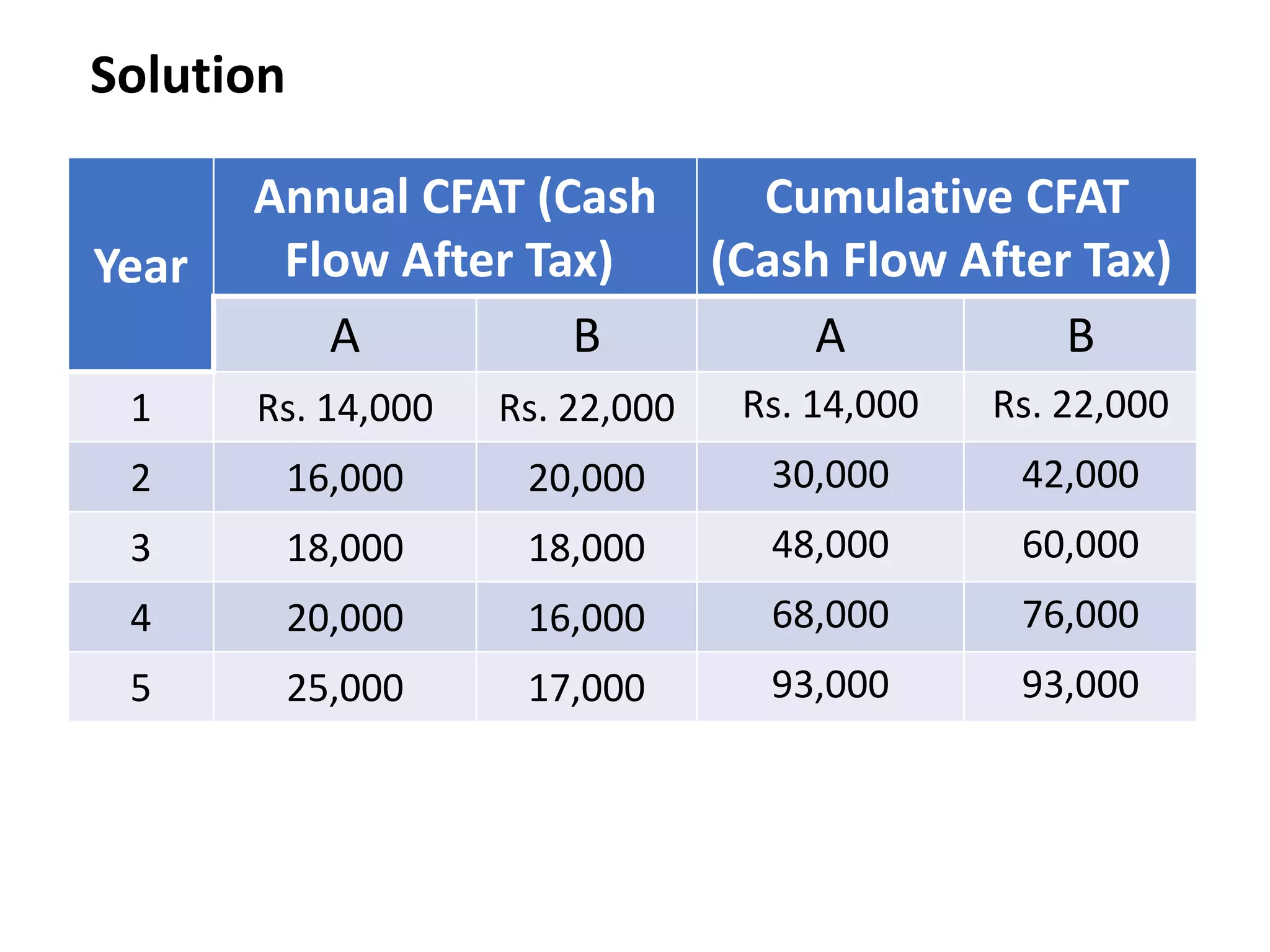
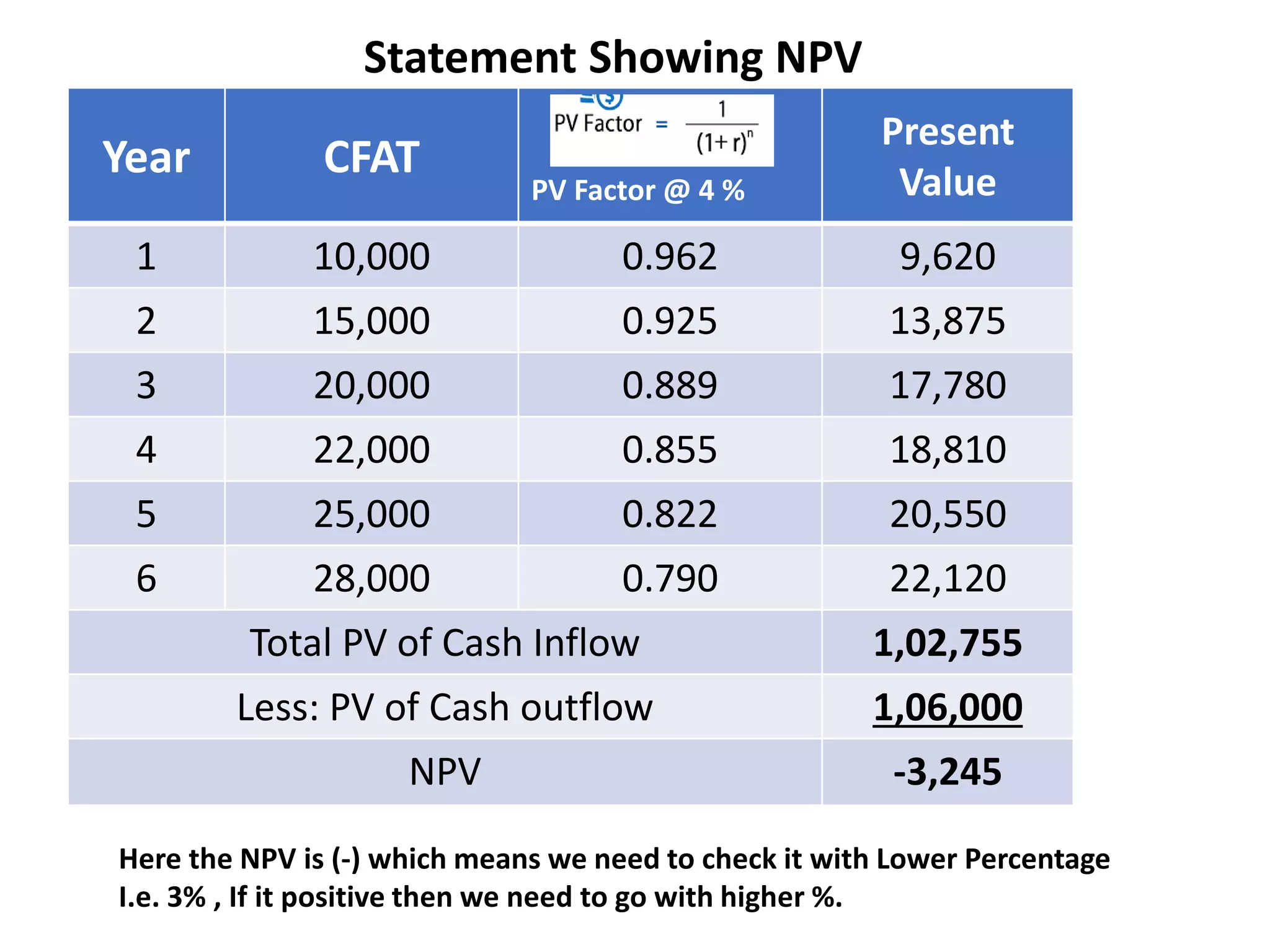
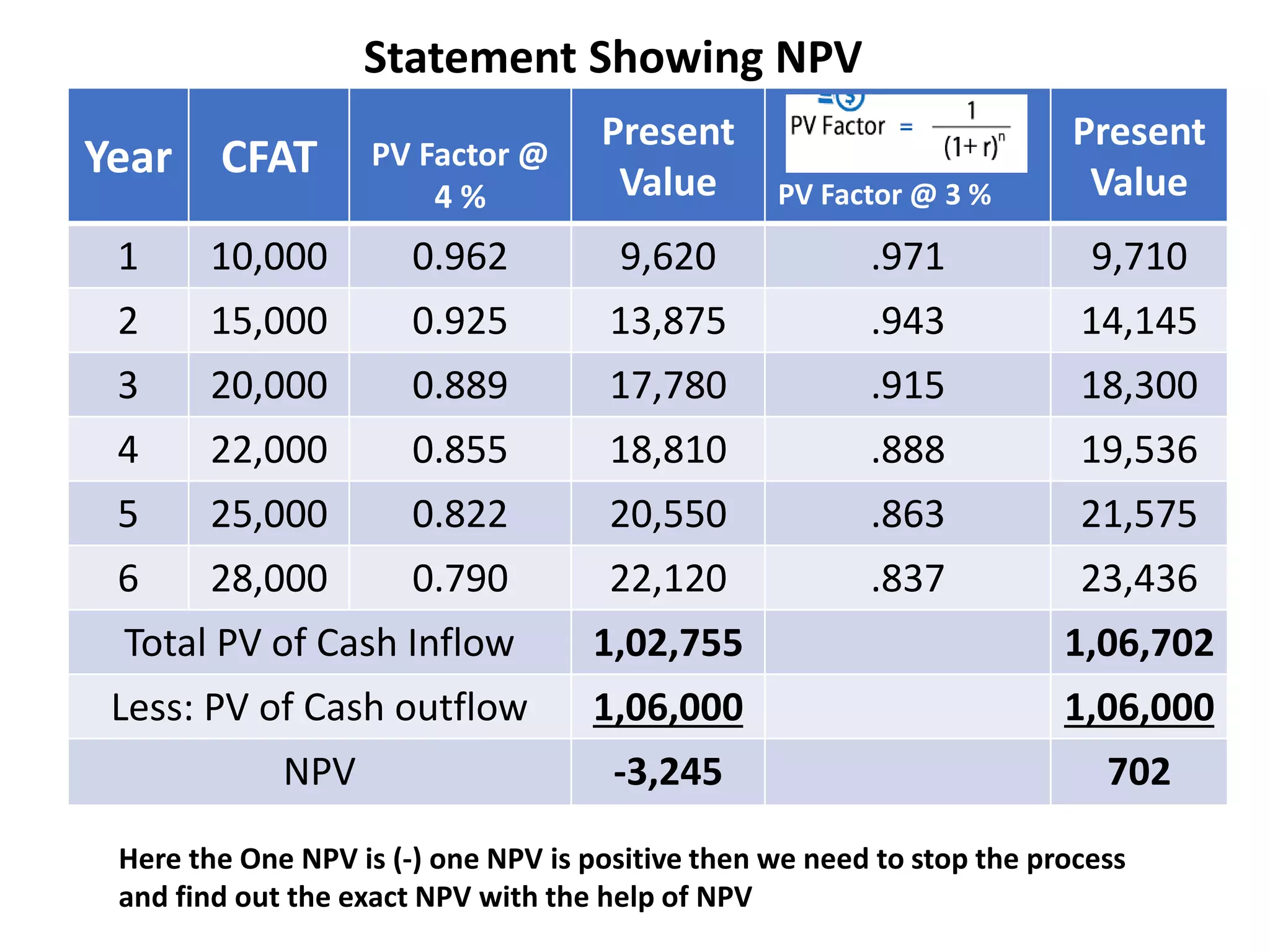
76. Calculation of Exact IRR
IRR = 3% + 702 x [4% - 3%]
1,06702 - 1,02,755
IRR = 3% + 702 x 1%
3,947
IRR = 3.18%

77. Profitability Index
• The Profitability Index (PI) measures the ratio between
the present value of future cash flows and the initial
investment. The index is a useful tool for ranking
investment projects and showing the value created per
unit of investment.
• The Profitability Index is also known as the Profit
Investment Ratio (PIR) or the Value Investment Ratio
(VIR).
• Profitability Index measures the present value of returns
per rupee invested. It is like NPV approach.
• A project will qualify for acceptance if its Profitability
Index exceeds one. When PI equals 1, the firm is
indifferent to the project.

78. Common
Problem

79. Problem:

80. Solution:

81. 1. Pay Back Period (PB)
Year
Annual CFAT
(Cash Flow After Tax)
Cumulative CFAT
(Cash Flow After Tax)
1 ₹ 10,000 ₹ 10,000
2 10,450 20,450
3 11,800 32,250
4 12,250 44,500
5 16,750 61,250
The recovery of the investment falls between the fourth and fifth
years. Therefore, the Pay Back is 4 years plus fraction of the fifth
year.
The fractional value = 5,500/16,750 (fifth year's CFAT)
= 0.328
Thus, The Pay back period is 4.328 years.

82. 2. Average Rate of Return (ARR)
• ARR = Average Income x 100
Average Investment
= ₹ 2,250 (₹ 11,250/ 5) x 100
₹ 25,000 (₹ 50,000/2)
ARR = 9%

83. 3. Net Present Value (NPV)
Year CFAT
PV Factor @
10%
Total PV
1 ₹ 10,000 0.909 9,090
2 ₹ 10,450 0.826 8,632
3 ₹ 11,800 0.751 8,862
4 ₹ 12,250 0.683 8,367
5 ₹ 16,750 0.621 10,401
Total PV 45,352
Less: Initital outlay 50,000
NPV (4,648)

84. 3. Profitability Index (PI)
PI = PV of Cash inflows
PV of Cash outflows
PI = ₹ 45,352
₹ 50,000
Profitability Index = 0.907

85. Thank you...